35t/h内循环流化床锅炉流动数值模拟*

王 擎 刘丛丛 肖剑波 刘洪鹏

(1.油页岩综合利用中心(东北电力大学)；2.华能应城热电有限责任公司)

内循环流化床锅炉是一种与传统鼓泡床和循环流化床不同的流化床类型，广泛应用于燃烧/气化煤、焚烧废弃物、吸附及脱硫等进程[1]。对内循环流化床流动特性的研究主要利用实验和数值模拟两种方法。大型工业化内循环流化床由于耗资巨大，且在特定工况下某些实验不能实现，因此主要利用基于流体动力学的数值模拟研究内循环流化床的流动特性。Lu H L等利用基于颗粒动力学理论的双流体模型研究了鼓泡床内二元混合颗粒的尺寸分离[2]。Zhang N等利用以能量最小多尺度模型为基础的欧拉多相流模型对150MWe循环流化床气、固流动进行了三维数值模拟，分析了炉膛气、固流动特性[3]。田凤国等采用离散单元法(DEM)数值模拟与实验相结合的方法研究了内循环流化床的气、固流动特性[4]。在上述模型的基础上，还出现了小室模型和能量最小多尺度模型[5]。笔者利用基于颗粒动力学理论的欧拉双流体模型对35t/h内循环流化床锅炉炉膛流动特性进行三维数值研究。

1 内循环流化床模型

气、固两相流动模型采用基于颗粒动力学理论的欧拉双流体模型[6]，湍流模型采用RNGk-εper phase湍流模型[7]，气、固曳力模型采用Gidaspow模型[8]。压力速度耦合选择Simple算法[9]，动量、湍动能和湍动耗散率采用一阶迎风离散格式，体积分数采用Quick离散格式。

1.1 几何模型与网格划分

35t/h内循环流化床锅炉为双锅筒横置式自然循环水管锅炉，采用炉内复合循环流化床燃烧方式，本体T形布置。锅炉前部为炉膛(图1)，中部为转折室和过热器，后部为对流受热面、省煤器和空气预热器，上部为卧式旋风分离器。锅炉采用平衡通风，密相区域正压，悬浮室和对流换热面区域负压，压力平衡点位于给煤口处。炉膛未燃尽颗粒进入悬浮室，并在炉膛上部进入旋风分离器实现分离，分离后颗粒沿分离器下端返料口重新进入密相区，实现内循环。

图1 35t/h内循环流化床锅炉炉膛结构简图

根据内循环流化床内部流场特性，利用代数生成法生成分区组合网格。由于整个炉膛计算域不规则，整体网格划分非常困难，因此将炉膛划分为互不重叠的子区域。各个子区域分别生成网格，再将各网格块连接成总体网格，且使相邻子区域交界面网格保持一致。其中对炉膛密相区网格进行了加密。整个炉膛采用混合网格划分方法，网格总数为102万(图2)。

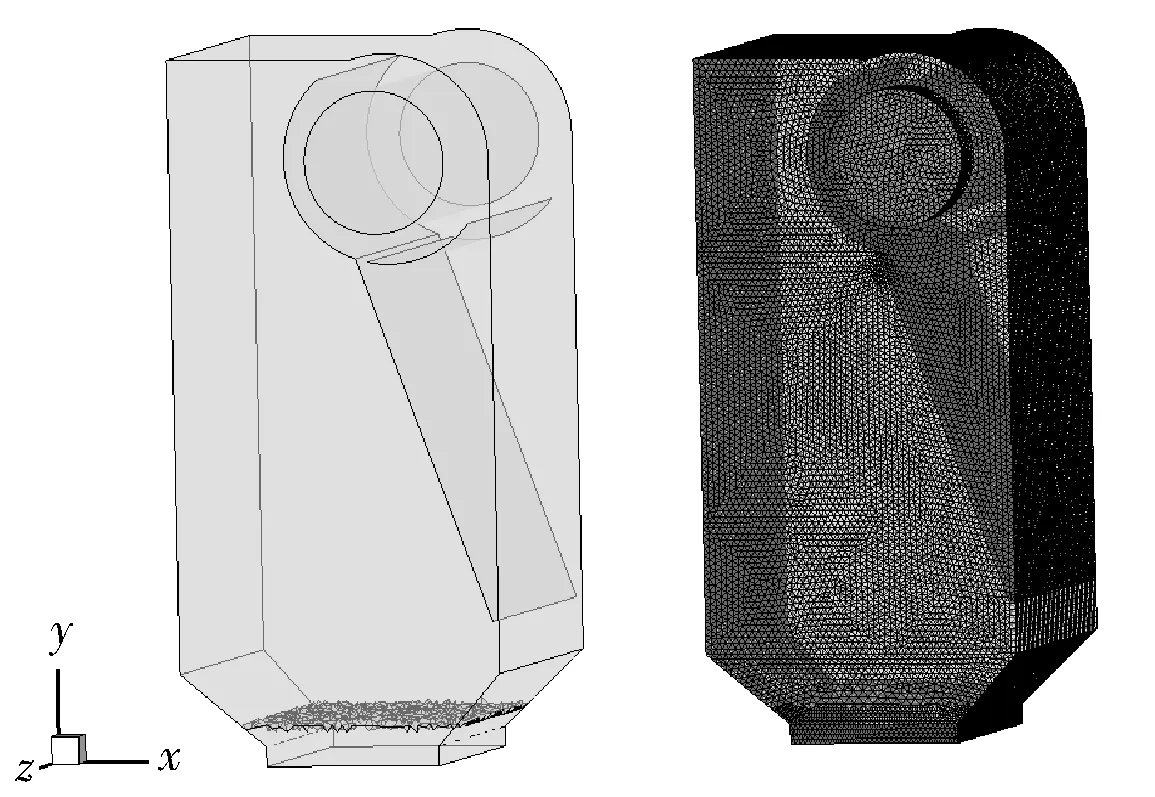
图2 35t/h内循环流化床三维模型及网格划分

气相密度和粘度均按冷态对应的值进行设定。气、固两相物性参数如下：

床温 850℃

气相密度 1.185kg/m3

气相粘度 15.50μPa·s

固相密度 2 200kg/m3

固相粘度 17.89μPa·s

固相直径 1.5mm

最大堆积体积分数 0.6

在壁面处，气相选择无滑移边界条件，固相选择部分滑移条件。初始条件和边界条件如下：

一次风速 20m/s

二次风速 8.59m/s

镜面反弹系数 0.5

碰撞恢复系数 0.99

循环倍率 5

炉膛出口压力 大气压

2 结果分析

2.1 模型验证

内循环流化床压差(炉膛静压与风室静压之差)是内循环床工程设计的重要参数，不仅表明了床内颗粒浓度的变化，而且为其协调控制提供依据。图3为不同风量下流化床压差的模拟值与实验值。由图3可见：炉膛压差的模拟值高于实验值，但两者的总体分布趋势一致，且吻合较好。说明选用的基于颗粒动力学理论的欧拉双流体模型能准确地描述炉膛内气、固两相的流动特性。

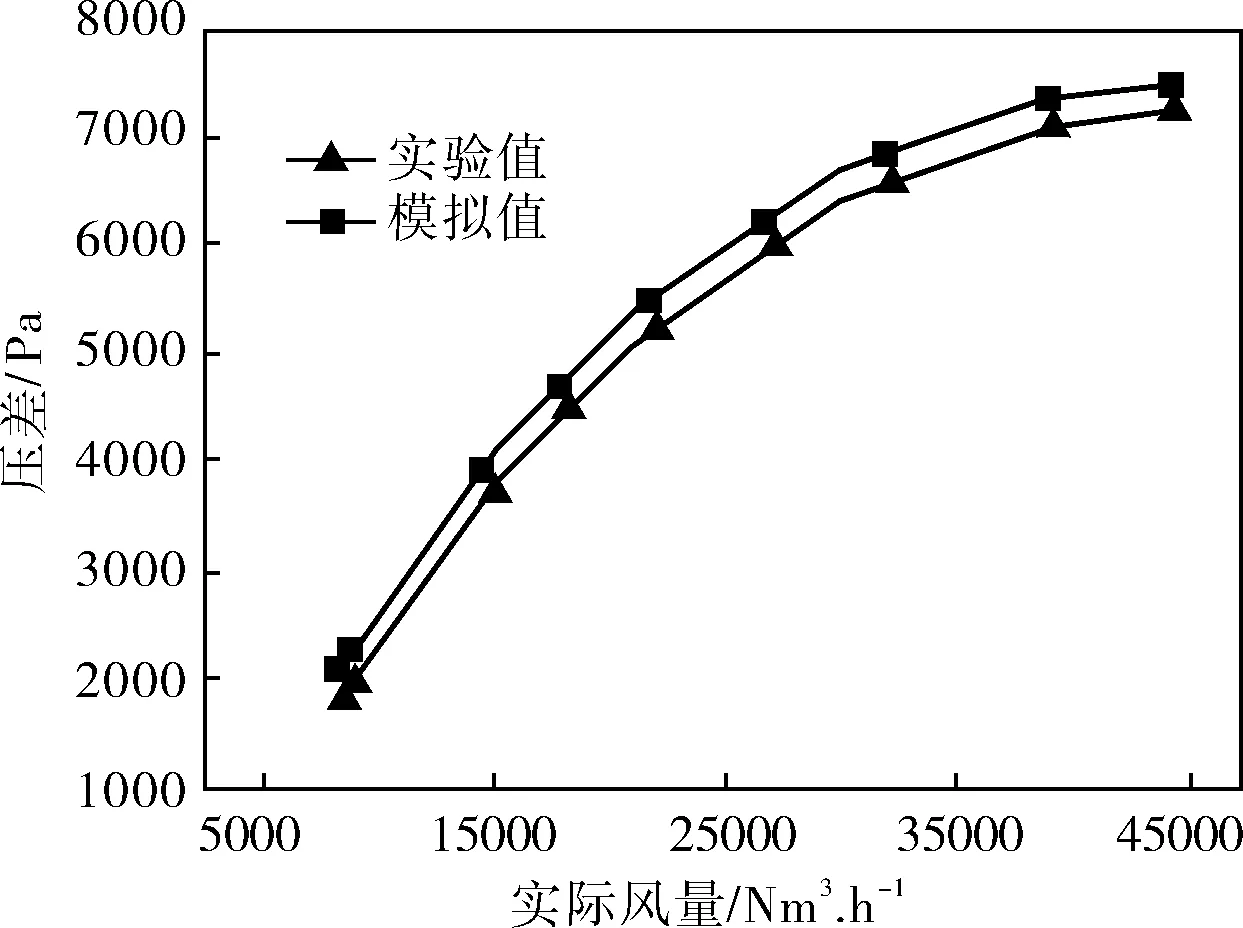
图3 不通风量下流化床压差模拟值与实验值

2.2 颗粒体积分数分布

图4、5给出了炉膛不同高度和不同垂直截面处1.5mm颗粒的体积分数分布情况。从图4可以看出：炉膛左、右两侧颗粒体积分数变化较大，尤其是炉膛右侧下部(旋风分离器挡板下端)和炉膛左侧上部；炉膛中心区域颗粒体积分数变化较小。结合图5可知，颗粒在边壁处浓度高，而在中心处浓度较低，此现象证实了环核结构的存在。炉膛左侧上部浓度较高是由于大量堆积颗粒沿壁面下降，同时又有大量颗粒重新在此堆积造成的。旋风分离器挡板下端浓度较高是由于炉膛内颗粒进入旋风分离器后，又由返料口重新进入炉膛底部造成此处颗粒浓度较高，说明颗粒在炉膛内的进行着内循环流动。

图4 不同垂直截面处1.5mm颗粒体积分数分布

图5 不同高度处1.5mm颗粒体积分数分布

从图5可以看出：y=2.2m截面在靠近分离器挡板下端位置处颗粒体积分数较大，这是由颗粒从分离器返料口重新进入炉膛底部，并在此重新流化造成的；y=4.8、7.5m截面在炉膛右侧分离器下端颗粒体积分数明显增加，这是由进入分离器的颗粒重新进入炉膛内造成的；y=10.0m截面在炉膛右侧颗粒体积分数较高，这是由颗粒进入分离器后还未返料就回流到炉膛堆积在此造成的。不同高度截面颗粒体积分数分布特性再次说明了颗粒的内循环特性。

2.3 颗粒速度分布

图6、7为挡板下端(y=2.2m)和分离器上部y=10.2m两个截面1.5mm颗粒水平速度分布特性。挡板下端截面位于分离器最下端返料口处，分离器上部截面位于分离器入口处。挡板下端截面处，颗粒速度在炉膛中心左侧为负值(-6～-3m/s)，在炉膛中心右侧为正值(3～7m/s)，说明颗粒不断地由返料口回到密相区；分离器上部截面处，颗粒速度在分离器左侧速度为负值(-8～-3m/s)，在分离器右侧为正值(3～8m/s)，说明颗粒不断地由炉膛上部稀相区涌入分离器中，并且在分离器中具有较大速度。

a. 挡板下端

b. 分离器上部

图7 挡板下端和分离器上部处颗粒水平速度

由于颗粒在分离器中速度较大，大部分颗粒会直接流向分离器右侧墙壁，且受重力影响，颗粒会下降到分离器右侧底部，进而从返料口重新进入密相区；而小部分颗粒在分离器左侧也会由于重力作用进入分离器左侧底部的返料口。这样进入分离器的颗粒重新回到密相区，形成了挡板下端处的颗粒特性曲线。同时从图7可以看出，两侧的速度分布十分不均匀，这是由单侧布置旋风分离器造成。由挡板下端截面和分离器上部截面颗粒速度分布特性的分析可得出，颗粒在内循环流化床炉膛内形成了周而复始的内循环流动。

3 结束语

笔者利用基于颗粒动力学理论的欧拉双流体模型对35t/h内循环流化床锅炉炉膛的气、固流动特性进行了三维数值研究。结果表明：炉膛压差的模拟值与实验值吻合好，说明欧拉双流体模型能够准确地描述炉膛内气、固流动特性；颗粒体积分数和速度分布特性揭示了内循环流化床中颗粒的内循环流动机理，为内循环流化床大型化和流动结构优化提供了参考。

[1] Feng Y Q, Swenser-Smith T,Witt P J, et al. CFD Modeling of Gas-solid Flow in an Internally Circulating Fluidized Bed[J]. Powder Technology, 2012, 219:78～85.

[2] Lu H L, He Y R,Gidaspow D, et al. Size Segregation of Binary Mixture of Solid in Bubbling Fluidized Beds[J]. Powder Technology, 2003, 134(1/2):86～97.

[3] Zhang N, Lu B N,Wang W,et al. 3D CFD Simulation of Hydrodynamics of a 150 MWeCirculating Fluidized Bed Boiler[J]. Chemical Engineering Journal, 2010, 162(2):821～828.

[4] 田凤国，章明川，范浩杰，等.内循环流化床颗粒流动特性的数值模拟[J].上海交通大学学报，2007，41(3)：347～351.

[5] 王擎，孙佰仲，吕海生，等．循环床炉内气固两相流动特性的数值模拟探讨[J].东北电力学院学报，2004，24(2)：1～5.

[6] Ding J M，Gidaspow D. A Bubbling Fluidization Model using Kinetic Theory of Granular Flow[J]. AIChE journal, 1990, 36 (4): 523～538.

[7] Wang Q, Xiao J B, Liu H P. CFD Simulation of Hydrodynamics on the Dense Zone on a 65t/h Oil Shale-fired High-low Bed CFB Boiler[J]. Powder Technology, 2013, 249: 339～352.

[8] Gidaspow D. Multiphase Flow and Fluidization[M]. Salt Lake City：American Academic Press，1994.

[9] Eckert E R G, Goldstein R J, Patankar S V, et al. Heat Transfer—A Review of 1980 Literature[J]. International Journal of Heat and Mass Transfer, 1981, 24(12): 1863～1902.