一类新的周期为的二元广义分圆序列的线性复杂度

李瑞芳 柯品惠



李瑞芳 柯品惠*

(福建师范大学网络安全与密码技术福建省重点实验室 福州 350007)

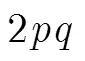
密码学；有限域；广义分圆序列；线性复杂度

1 引言

一条序列的线性复杂度定义为生成该序列的最短的线性移位寄存器的长度。在密码学等相关领域的应用中，伪随机序列必须具有高的线性复杂度[1,2]。从安全的角度讲，一条好的序列往往要求它的线性复杂度必须不小于其周期长度的一半。

易验证，

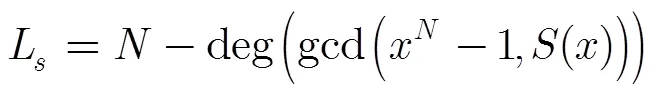
3 线性复杂度

本节将计算第2节定义的广义分圆序列的线性复杂度，为此，需要如下引理。

定义如式(5)辅助多项式：

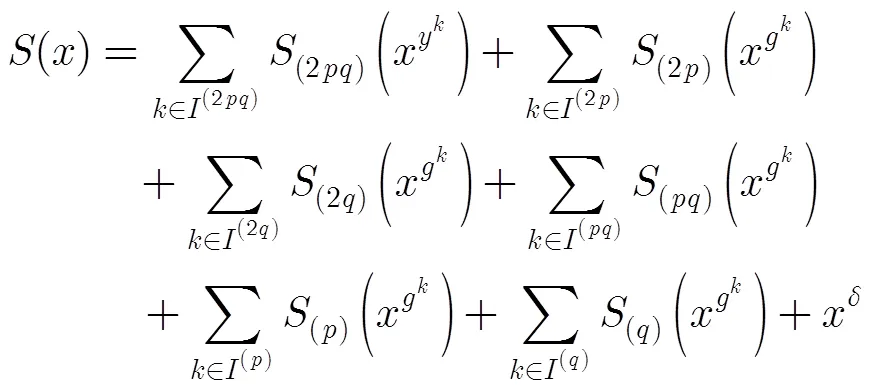
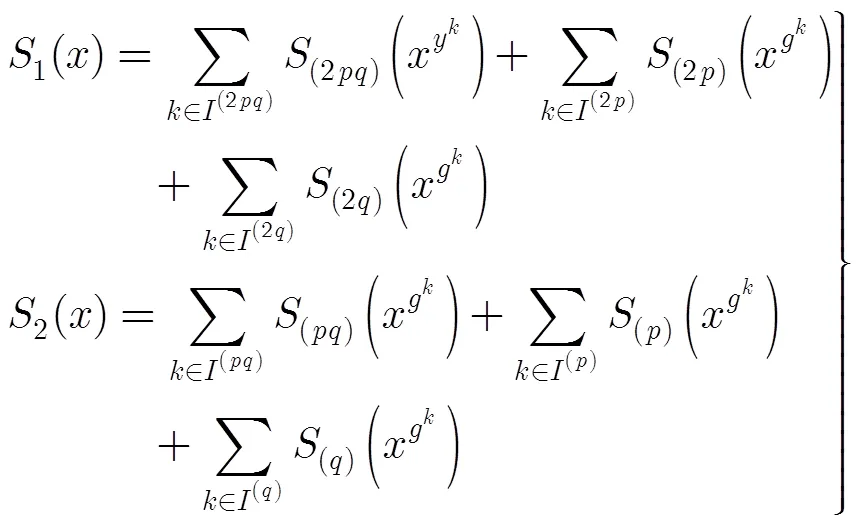
则

由于不同专家之间的意见不同，需要将专家的意见作为证据进行证据融合。融合证据之前，运用式(5)—式(7)计算折扣后的证据BPA,再运用式(8)对各证据的BPA进行融合。

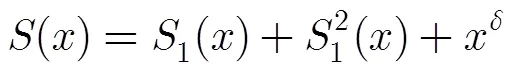
由式(4)，序列的线性复杂度为

证毕

记

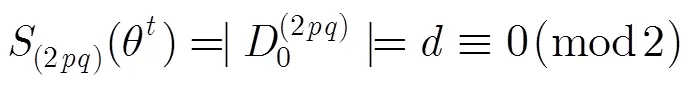
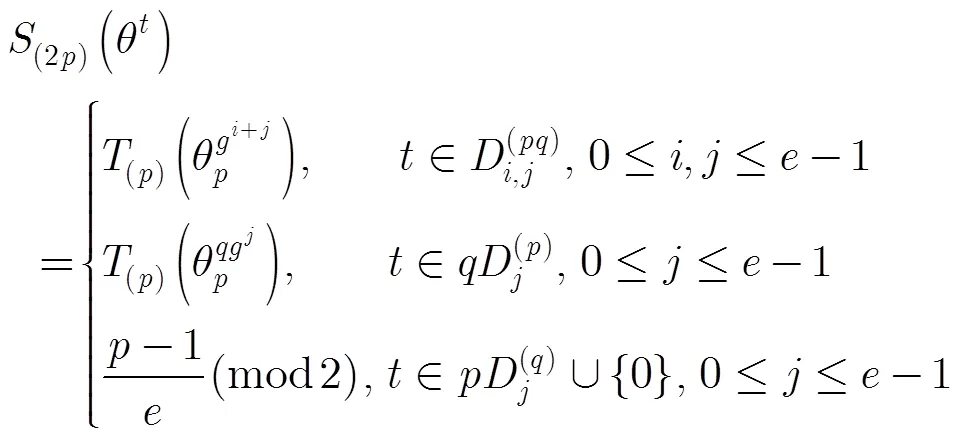
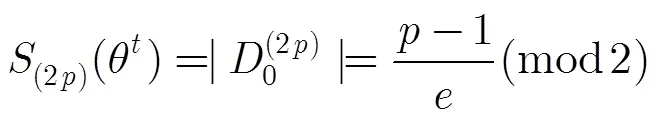
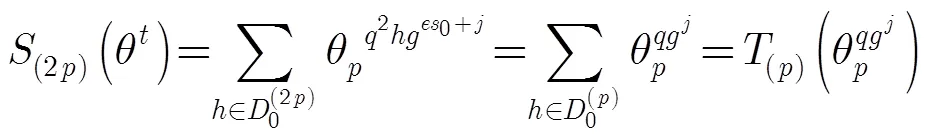
综上，可知结论成立。 证毕

类似于引理4，容易证明引理5。

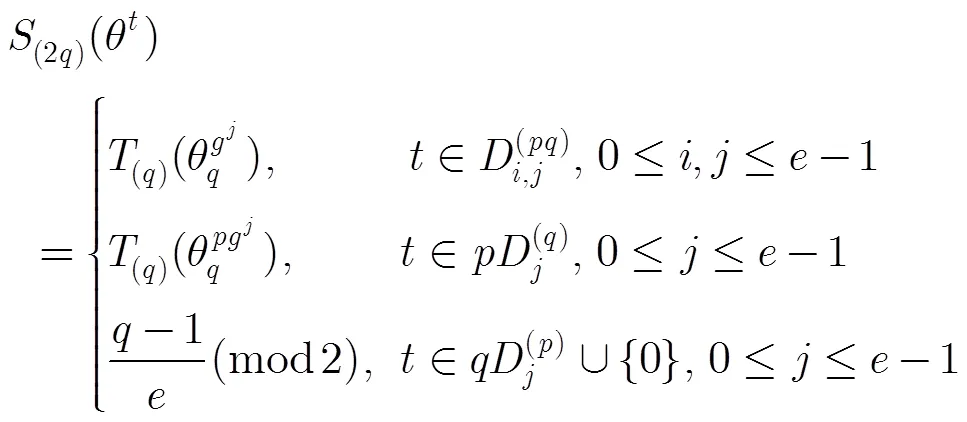
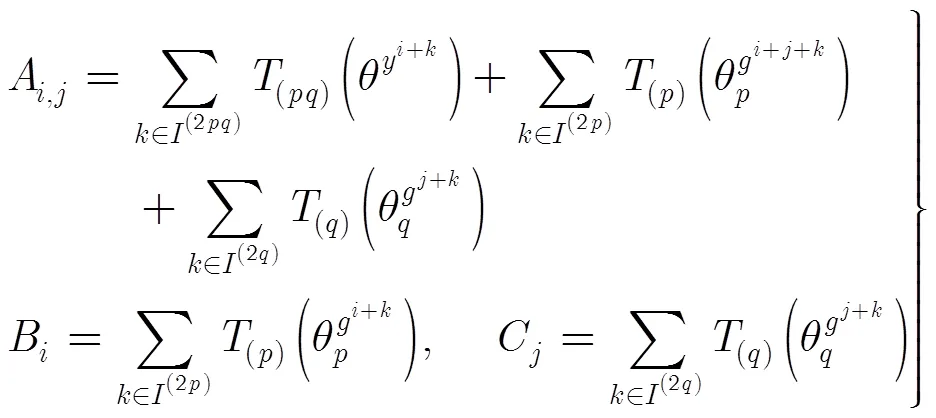
及

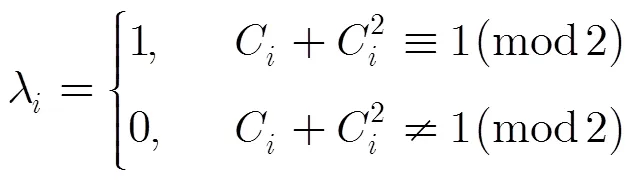
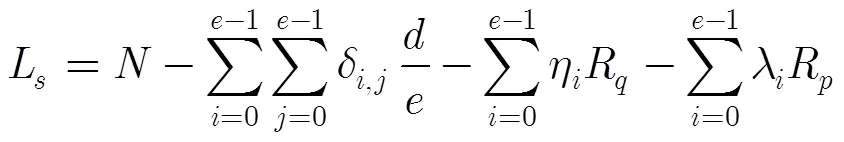
由引理2得，

证毕

4 结论

[1] Golomb S W and Gong G. Signal Design for Good Correlation: For Wireless Communications, Cryptography and Radar Applications[M]. Cambridge: UK, Cambridge University Press, 2005: 174-175.

[2] Cusick T, Ding C, and Renvall A. Stream Ciphers and Number Theory[M]. Amsterdam: The Netherlands, North- Holland Mathematical Library 55, 1998: 198-212.

[3] Ding C and Helleseth T. Generalized cyclotomy and its applications[J]., 1999, (4): 467-474.

[4] Ding C, Hellseth T, and Shan W. On the linear complexity of Legendre sequences[J]., 1998, 44(3): 1276-1278.

[5] Kim Y J, Jin S Y, and Song H Y. Linear complexity and autocorrelation of prime cube sequences[J]., 2007, 4851: 188-197.

[6] Kim Y J and Song H Y. Linear complexity of prime n-square sequences[C]. IEEE International Symposium on Information Theory, Toronto, Canada, 2008: 2405-2408.

[7] Yan T, Sun R, and Xiao G. Autocorrelation and linear complexity of the new generalized cyclotomic sequences[J]., 2007, E90-A: 857-864.

[8] Yan T, Li S, and Xiao G. On the linear complexity of generalized cyclotomic sequences with the periodp[J].2008, (21): 187-193.

[9] Edemskiy V. About computation of the linear complexity of generalized cyclotomic sequences with periodp+1[J]., 2011, 61(3): 251-260.

[10] Zhang J W, Zhao C A, and Ma X. Linear complexity of generalized cyclotomic binary sequences of length 2p[J]., 2010, (21): 93-108.

[11] Ke P H, Zhang J, and Zhang S Y. On the linear complexity and the autocorrelation of generalized cyclotomic binary sequences of length 2p[J].2012, 67(3): 325-339.

[12] Ke P H and Zhang S Y. New classes of quaternary cyclotomic sequence of length 2pwith high linear complexity[J]., 2012, 12(16): 646-650.

[13] Hu L Q, Yue Q, and Wang M H. The linear complexity of Whiteman’s generalized cyclotomic sequences of periodp+1q+1[J]., 2012, 58(8): 5534-5542.

[14] Du X N and Chen Z X. A generalization of the Hall’s sixtic residue sequences[J]., 2013, 222: 784-794.

[15] Chang Z L and Li D D. On the linear complexity of generalized cyclotomic binary sequences of length 2[J]., 2013, DOI: 10.1002/cpe.3052.

李瑞芳： 女，1988年生，硕士生，研究方向为序列设计.

柯品惠： 男，1978年生，副教授，主要研究方向包括序列设计、现代密码学中的布尔函数.

Li Rui-fang Ke Pin-hui*

(,,350007,)

Crpytography; Finite fields; Generalized cyclotomic sequence; Linear complexity

TN918.1

A

1009-5896(2014)03-0650-05

10.3724/SP.J.1146.2013.00751

2013-05-27收到，2013-08-12改回

国家自然科学基金(61102093)资助课题

柯品惠 keph@fjnu.edu.cn