星载多基线InSAR理想相位图的快速仿真方法

葛仕奇 刘光炎



星载多基线InSAR理想相位图的快速仿真方法

葛仕奇*刘光炎

(南京电子技术研究所 南京 210039)

针对星载多基线干涉合成孔径雷达(InSAR)系统，该文研究并提出了基于数字高程模型(DEM)数据、卫星轨道和基线信息的干涉相位的快速仿真方法。利用前向地理编码进行星载InSAR几何约束下的DEM模型匹配，完成多基线InSAR干涉相位生成，并通过多项式近似和混合迭代实现对模型匹配过程的优化。理论分析和仿真实验表明，该方法在显著提高计算效率的同时，保持了较高的相位生成精度，并且对复杂DEM模型有很好的迭代收敛性，适于实现对大场景复杂地形的星载多基线干涉相位快速仿真。

干涉合成孔径雷达；多基线；相位仿真；地理编码

1 引言

星载干涉合成孔径雷达(InSAR)能够全天时、全天候地提取大范围地区的数字高程模型(DEM)[1]，而多基线InSAR技术通过对多通道数据的联合处理，可以降低相位解缠难度并提高DEM的提取精度[2,1]，是航天对地观测领域的研究热点之一。干涉数据仿真在星载多基线InSAR系统设计中十分重要，其最基本的方法是以SAR回波仿真为基础[4]，这种方法对体散射、有限信噪比等非理想因素的模拟最接近实际情况，但是运算量巨大，且由于处理环节多而不适于控制相位生成精度。本文主要研究基于场景DEM数据、卫星轨道和基线信息直接生成多基线干涉相位图，利用这种方法可以得到精确反映地形变化的相位信息，因而可准确预测不同基线长度和倾角等系统参数下的干涉条纹特性、雷达图像中的叠掩和阴影区域、以及局地几何去相干等信息[5]，为系统优化设计提供依据；另外对仿真干涉相位可以定量引入后向散射模型和噪声模型，便于对相位解缠、高程反演等算法进行可控误差分析，从而实现对算法性能的定量评估[6]。此外，利用该方法生成的高精度地形参考相位，还可以应用于差分干涉SAR系统的信号处理中，具有较为广泛的应用范围。

对于干涉相位图的仿真，常用方法是对已知DEM数据进行坐标变换，得到DEM均匀栅格点在雷达图像坐标系中的映射点并赋予对应的干涉相位[7]，但是该方法涉及非均匀插值重采样，不仅降低了仿真精度，而且增加了运算负担。文献[5]提出了一种可用于大场景的常规InSAR相位快速仿真方法，其核心思想是利用多项式快速生成算法和对稀疏采样点的内插降低运算量。文献[8]进一步研究了在星载立体、双基地干涉模型下的干涉相位生成问题，并分析了相位生成精度。在多基线InSAR相位图仿真方面，文献[9,10]提出了多基线InSAR系统的相位仿真方法，该方法以机载模型为基础，不适用于星载SAR构像模型下的干涉相位生成。本文在深入研究星载雷达成像系统严密构象模型的基础上，提出了一种基于前向地理编码的星载多基线InSAR干涉相位图快速仿真方法，该方法可以在保证相位生成精度的同时，显著提高运算效率，最后通过对仿真实验，验证了该方法的有效性。

2 星载多基线InSAR干涉相位生成原理

2.1 星载InSAR严密构像模型

在图1所示的星载多基线InSAR系统中，一般以主星为参考，两颗辅星获得的SAR影像均根据主星成像结果进行配准生成干涉相位。相应地，在InSAR相位仿真中，首先需要精确建立主星成像平面中各采样点与场景DEM数据间的映射关系，这一过程可基于星载雷达图像的构像模型通过坐标变换来实现[11]。目前国内外采用的雷达图像构像模型有Leberl模型，Konecny模型和距离-多普勒模型(R-D模型)等[12]，其中R-D模型可以直接利用星历数据，根据雷达成像时的距离条件和多普勒频移条件，建立SAR成像瞬间严格的物像关系，在地固坐标系(ECR)中可用3个方程共同描述该模型，即距离方程：

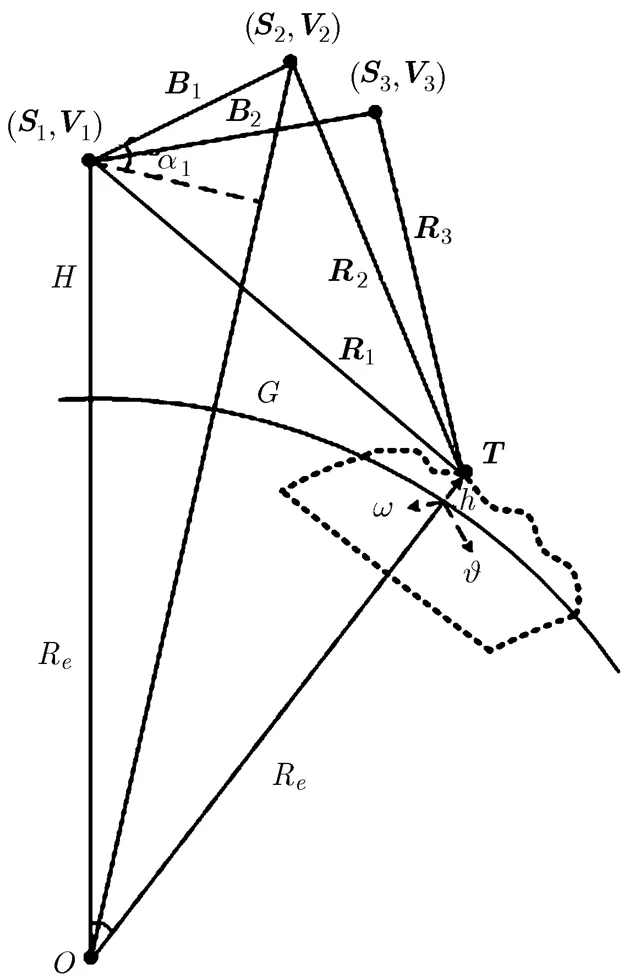
图1星载多基线InSAR系统几何构型图

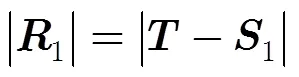
多普勒方程：

以及地球椭球模型方程：

基于R-D模型，能够建立成像目标点在主星雷达图像坐标与场景地理坐标之间的非线性映射关系，接下来还需要进一步根据基线信息完成多基线InSAR相位的生成。

2.2 多基线干涉相位生成

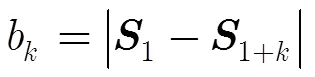
辅星轨道高度方程：

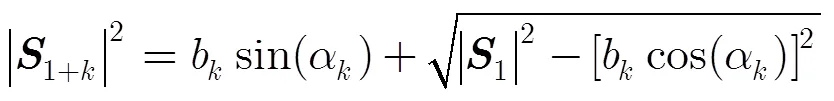
以及辅星多普勒方程：

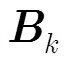
3 大场景星载InSAR相位图的快速生成方法

基于上述原理，本文提出了一种高效的星载多基线干涉相位仿真方法，实现流程如图2。

图2 基于前向地理编码的星载多基线干涉相位仿真流程图

从计算的角度看，解上述两个方程组需要解非线性空间的几何方程组，而且式(1)~式(3)的求解嵌套在匹配定位过程中，这些计算都需要迭代处理，随着仿真场景的增大，计算时间将迅速增加，故需要对前向地理编码和匹配定位过程做进一步优化。

3.1 前向地理编码的优化

其中，系数和可以由个假定高程及其对应的定位结果经多项式拟合获得，而阶数取决于对多项式近似误差的分析。根据图1，目标点地距为

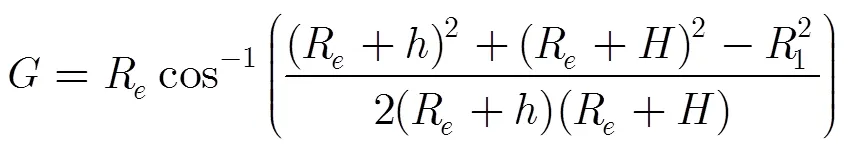
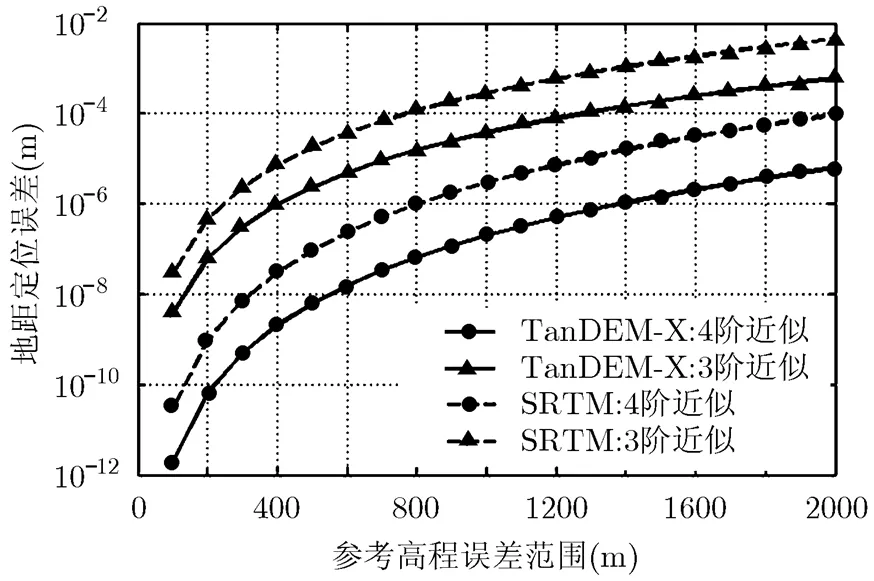
图3 InSAR定位误差随参考高程误差的分布曲线

3.2 匹配定位的快速实现

匹配定位中需要迭代更新参考高程，常规方法是采用不动点迭代( Fixed Point Iteration,

第1步 构造匹配目标函数

第3步 通过混合迭代算法逐步缩小解区间范围，以最佳逼近DEM曲面。在混合迭代中，首先按照式(11)对目标函数进行反二次插值，如果插值结果使目标函数的绝对值减小了，并且使解区间至少减半，那么就以插值结果更新解区间边界。

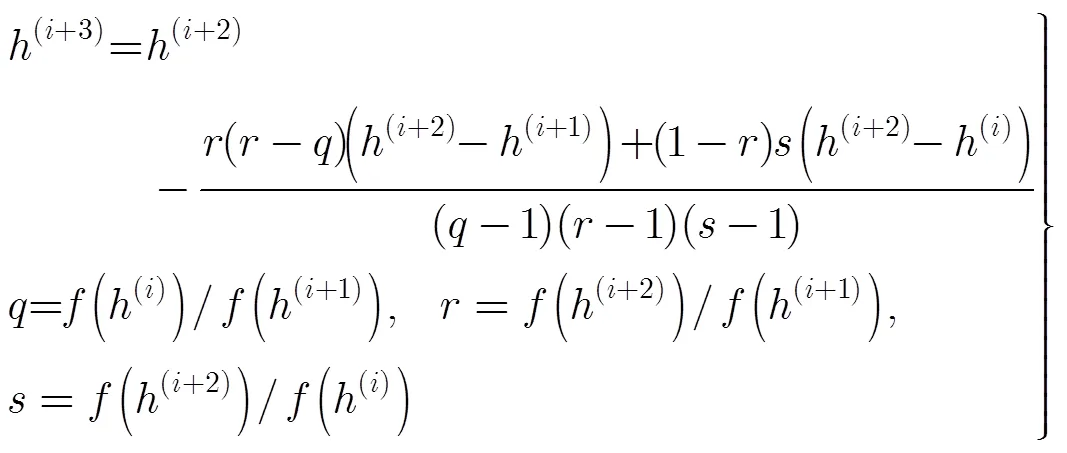
否则，按照式(12)对目标函数进行割线插值，并采用与之前同样的准则判定是否用插值结果更新解区间边界。

如果割线插值也失败，最后可利用当前解区间的均值重新定界：

由于反二次插值和割线插值分别实现了对场景局部曲面的二次拟合和线性拟合，而均值定界是基于二分法的原理，因此收敛速度依次降低；但是，高阶插值存在发散的可能，而均值插值可以保证解的收敛性，故采用混合迭代可以保证对复杂地形的高效率匹配。

4 仿真实验及分析

表1星载InSAR系统参数

轨道高度(km)下视角(°)PRF(Hz)干涉图分辨率(m) 511.9735.53832.53×3

实验1对图4(a)所示的多山DEM模型进行仿真分析，场景最高点为81.06 m。系统工作期间的空间基线变化保持在5%以内，且基线长度分别在406.9 m和634.6 m附近变化。

首先采用混合迭代得到的匹配定位输出结果如图4(b)所示，然后根据动态变化的基线信息计算不同时刻的辅星位置后，可得到干涉相位仿真结果，如图5所示。可见，实验结果正确反映了地形和基线对干涉条纹的影响。

实验2在系统参数不变的情况下，对图6(a)所示的某山区实际DEM数据进行仿真，最高点为112.34 m。由于该场景地形起伏更加复杂，可验证本文方法的效率和收敛性，图6 (b)为仿真得到的干涉相位图(左)以及去平地相位图(右)。

作为对比，表2给出了不同收敛阈值情况下，采用FPI方法和本文方法在平均迭代次数和发散点数方面的比较。可见FPI方法存在不同程度的迭代发散现象，而本文方法不存在该问题，而且具有较高的匹配效率。

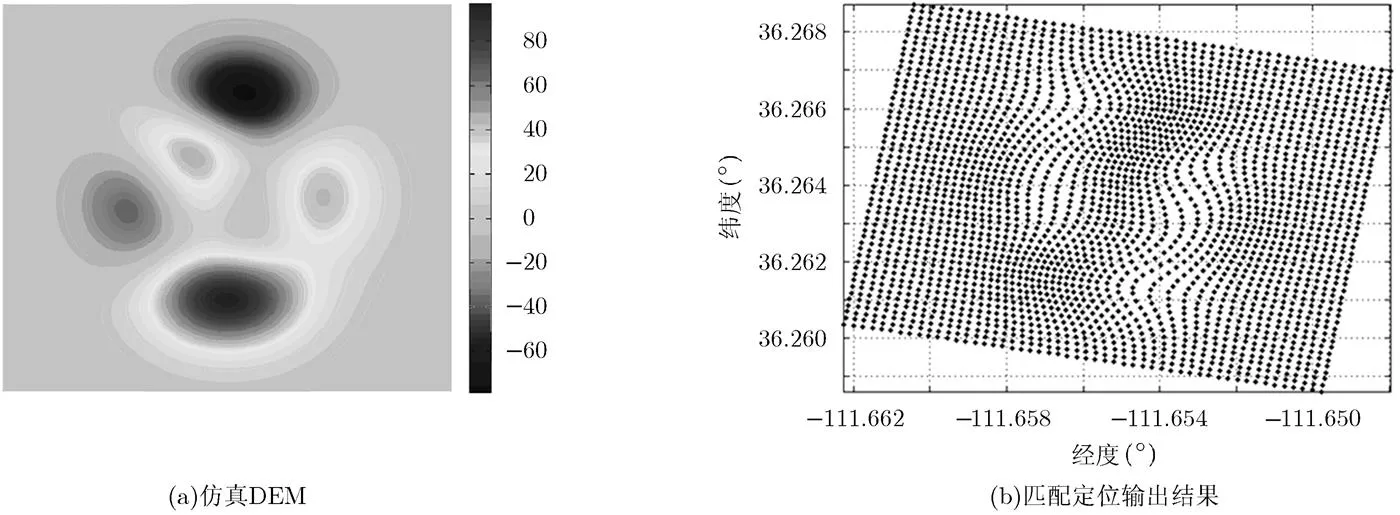
图4 实验DEM模型

图5 仿真DEM模型的多基线干涉相位(图像大小512×512点，分辨率3 m)

图6 实际DEM模型及干涉相位仿真结果(图像大小512×512点)

最后，分析本文方法的效率，第1步通过预处理生成前向地理编码多项式，第2步采用混合迭代法完成匹配定位，而第3步根据动态基线信息生成干涉相位。表3比较了优化前后各步运算的耗时，优化前的方法在FPI迭代过程中又嵌套了解方程组式(1)~式(3)所需进行的牛顿-拉费森迭代，计算效率极低。经优化后，不仅通过混合迭代降低了匹配定位的迭代次数，而且通过增加对前向地理编码多项式的系数拟合这个预处理步骤，使单次迭代的运算量显著减小。此外，通过均匀抽取控制点并计算得到干涉相位真值，以此为标准统计分析干涉相位生成精度，可得干涉相位的误差均方根值为0.000559 rad。

表2 迭代性能比较

表3干涉相位仿真效率分析

值得注意的是，一旦预处理和匹配定位完成，对星载多基线InSAR系统可重复利用前两步得到的定位结果，快速实现不同基线情况下的理想干涉相位图仿真。

5 结束语

星载多基线InSAR是对常规InSAR技术扩展后形成的一种新型航天对地观测手段，干涉相位图仿真在该新兴技术的研究中具有十分重要的意义。本文针对星载多基线InSAR系统构型，提出了一种基于前向地理编码的多基线干涉相位图快速仿真方法，该方法不仅提高了仿真效率，而且对复杂地形的干涉相位仿真有较好的收敛性，为星载多基线干涉相位图的进一步应用研究奠定了基础。后续工作还需考虑叠掩和阴影对干涉图的影响，叠掩是指当迎坡坡度大于雷达下视角时，可能出现几何上的多个点被叠加为一个点的情况；阴影是指当背坡坡度大于雷达俯角时，雷达波束被遮挡而无法到达的区域。下一步工作应分别进行叠掩和阴影区的识别与标注，从而更准确地反映输入场景在给定系统参数下的干涉相位图。

[1] Chang Wen-yen, Wang Chih-tien, Chu Chih-yuan,.. Mapping geo-hazard by satellite radar interferometry[J]., 2012, 100(10): 2835-2850.

[2] Yu Han-wen, Li Zhen-fang, and Bao Zheng. A cluster-analysis-based efficient multibaseline phase unwrapping algorithm[J]., 2011, 49(1): 478-487.

[3] Yuan Zhi-hui, Li Fei, Deng Yun-kai,.. Multichannel InSAR DEM reconstruction through closed-form robust Chinese remainder theorem[C]. IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Munich, 2012: 4006-4009.

[4] He Zhi-hua, He Feng, Dong Zhen,.. Real-time raw-signal simulation algorithm for InSAR hardware-in-the-loop simulation applications[J]., 2012, 9(1): 134-138.

[5] Eineder M. Efficient simulation of SAR interferograms of large areas and of rugged terrain[J]., 2003, 41(6): 1415-1427.

[6] 李文强, 李景文, 陈杰. 一种干涉SAR复图像数据的快速仿真方法[J]. 北京航空航天大学学报, 2005, 31(1): 32-35.

Li Wen-qiang, Li Jing-wen, and Chen Jie. Fast simulation of complex image for interferometric SAR[J]., 2005, 31(1): 32-35.

[7] Goblirsch W. The exact solution of the imaging equations for crosstrack interferometers[C]. IEEE Proceedings of International Geoscience and Remote Sensing Symposium, Singapore, 1997: 439-441.

[8] 王青松, 黄海风, 董臻, 等. InSAR 理想干涉相位计算的快速方法及精度分析[J]. 系统仿真学报, 2009, 21(18): 5951-5954.

Wang Qing-song, Huang Hai-feng, Dong Zhen,.. Fast simulation of InSAR ideal interferometric phase and precision analysis[J]., 2009, 21(18): 5951-5954.

[9] 张红敏, 靳国旺, 徐青, 等. 多基线InSAR干涉图仿真方案设计与分析[J]. 系统仿真学报, 2012, 24(7): 1516-1522.

Zhang Hong-min, Jin Guo-wang, Xu Qing,.. Design and analysis of interferograms simulation methods for multi-baseline InSAR[J]., 2012, 24(7): 1516-1522.

[10] Zhang Hong-min, Jin Guo-wang, Xu Qing,. Simulation of interferograms for multi-baseline InSAR study[C]. 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, 2009: 408-411.

[11] Frey O, Santoro M, Werner C,.. DEM-based SAR pixel-area estimation for enhanced geocoding refinement and radiometric normalization[J]., 2013, 10(1): 48-52.

[12] Xu Hua-ping, and Kang Changhui. Equivalence analysis of accuracy of geolocation models for spaceborne InSAR[J]., 2010, 48(1): 480-490.

[13] 仇晓兰, 韩传钊, 刘佳音. 一种基于持续运动模型的星载SAR几何校正方法[J]. 雷达学报, 2013, 2(1): 54-59.

Qiu Xiao-lan, Han Chuan-zhao, and Liu Jia-yin. A method for spaceborne SAR geolocation based on continuously moving geometry[J]., 2013, 2(1): 54-59.

[14] Kim M and Hwang C. A polynomial-based ortho-rectification for SAR imagery[C]. 5th International Congress on Image and Signal Processing (CISP), Chongqing, 2012: 997-1000.

[15] Geudtner D, Zink M, Gierull C,.. Interferometric alignment of the X-SAR antenna system on the space shuttle radar topography mission[J]., 2002, 40(5): 995-1006.

[16] Zink M. TanDEM-X mission status[C]. IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Munich, 2012: 1896-1899.

[17] 郭交, 李真芳, 刘艳阳, 等. 基于粗数字高程模型信息的干涉相位图生成方法[J]. 电子与信息学报, 2010, 32(11): 2642-2647.

Guo Jiao, Li Zhen-fang, Liu Yan-yang,.. Approaches to interferogram generation based on coarse DEM[J].&, 2010, 32(11): 2642-2647.

葛仕奇： 男，1984年生，博士，研究方向为干涉合成孔径雷达、实时信号处理等.

刘光炎： 男，1967年生，研究员，研究方向为信号处理、SAR/ InSAR系统设计及成像等.

Fast Simulation Method of Ideal Phase Map for Spaceborne Multi-baseline InSAR

Ge Shi-qi Liu Guang-yan

(,210039,)

Based on Digital Elevation Mode (DEM) data, satellite orbit and baseline information, a kind of fast interferometric phase simulation method is investigated and presented for spaceborne multi-baseline InSAR system. By taking advantage of forward geocoding, the match of DEM model under strict spaceborne InSAR geometry is utilized to realize multi-baseline interferometric phase generation, and the match process is further optimized by polynomial approximation and hybrid iteration. Theory analysis and simulation experiments indicate that the proposed method can improve the computation efficiency with enough phase accuracy, as well as better iteration convergence property for complicated DEM model. Consequently, the method is suitable for efficient simulation of spaceborne multi-baseline InSAR interferometric phase for large and rugged terrain.

Interferometric SAR (InSAR); Multi-baseline; Phase simulation; Geocoding

TN959.3

A

1009-5896(2014)03-0571-06

10.3724/SP.J.1146.2013.00604

2013-05-03收到，2013-11-08改回

葛仕奇 raymond2464@126.com