基于非线性机会约束规划的多基雷达系统稳健功率分配算法

严俊坤 刘宏伟 戴奉周 罗 涛 保 铮



基于非线性机会约束规划的多基雷达系统稳健功率分配算法

严俊坤*刘宏伟 戴奉周 罗 涛 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

现有多基雷达系统(MSRS)功率分配算法都假设目标的雷达散射截面(RCS)信息先验已知。针对上述问题，该文将目标的RCS建模为分布未知的随机变量，提出一种基于非线性机会约束规划(NCCP)的MSRS稳健功率分配算法，用于处理RCS参数的不确定性。该文首先推导了目标跟踪误差的贝叶斯克拉美罗界(BCRLB)。然后以最小化MSRS各个时刻发射功率为目标，在满足BCRLB不大于给定误差的概率超过某一置信水平的条件下建立了NCCP模型，并用条件风险价值(CVaR)松弛结合抽样平均近似(SAA)算法对此问题进行了求解。最后，仿真实验验证了算法的有效性和稳健性。

多基雷达系统；功率分配；机会约束规划

1 引言

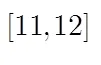
本文在上述研究的基础上，针对目标跟踪时RCS这个随机因素，提出了一种基于非线性CCP(NCCP)[13]的MSRS稳健功率分配算法。目的是使MSRS能动态地协调各部雷达的发射参数，进而在满足机会约束的条件下，尽可能地节约功率资源。本文首先推导了目标跟踪误差的BCRLB。然后，以最小化MSRS各个时刻发射功率为目标，在满足BCRLB不大于给定误差的概率超过某一置信水平的条件下建立了NCCP模型，并用条件风险价值(CVaR)[14]松弛结合抽样平均近似(SAA)[15]算法对此问题进行了求解。在仿真实验中，利用UHF波段和S波段的两组实测RCS数据以及一组频段更高的模拟数据进行验证，并将本文算法与文献[9]提出的算法(将目标RCS的转移模型设定为一阶Markov过程)进行了比较，实验结果证明了本文算法的有效性和鲁棒性。

2 数学模型

2.1目标运动模型

假设一个目标在平面内做匀速运动，目标的运动方程可写为

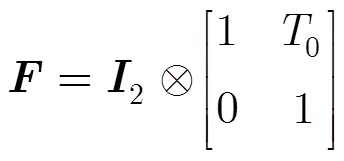
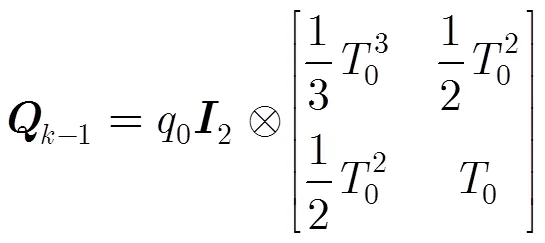
2.2观测模型

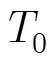
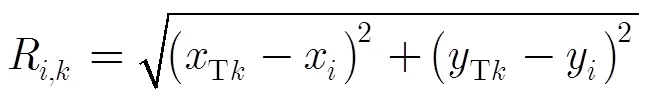
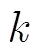
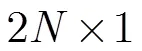
根据这些信息，融合中心可以对目标进行跟踪，目标的非线性观测方程可描述为

3 基于NCCP的功率分配算法

从数学上来讲，本文提出的功率分配算法可描述为：以目标跟踪精度不大于给定误差的概率超过某一置信水平为前提，最小化MSRS的消耗功率。在各个融合时刻，目标的贝叶斯信息矩阵(BIM)是各部雷达发射功率的函数，而由BIM求逆得到的BCRLB给目标的跟踪精度提供了一个衡量尺度[16]。因此，本文以跟踪误差的BCRLB为约束函数，建立了基于NCCP的功率分配模型。该模型将目标的RCS看作随机变化的不确定参数，在其发生一定程度的波动时，仍能节省MSRS的功率资源。具体步骤描述如下。

3.1 BIM的推导

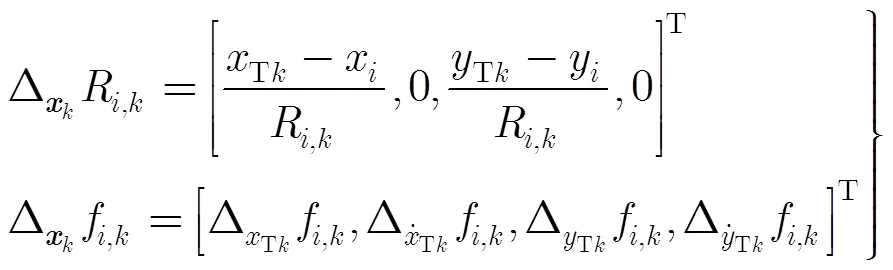
其中

3.2约束函数的构建

3.3 NCCP模型的建立

3.4 NCCP模型的求解

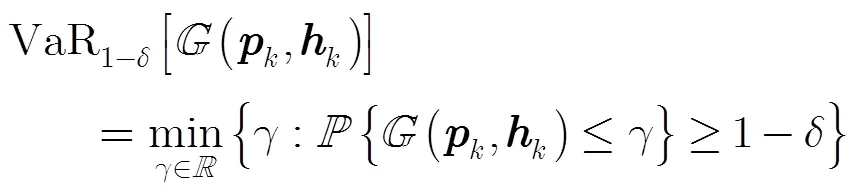
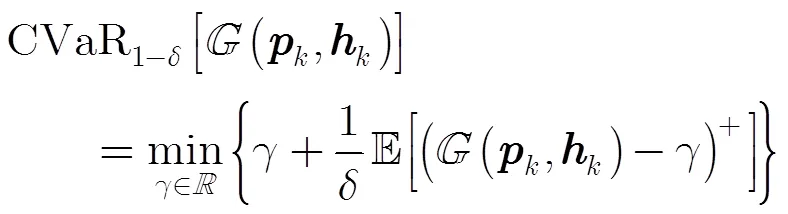
4 实验结果分析

图1 雷达与目标的空间位置关系

首先定义性能指标—功率节省率如下：

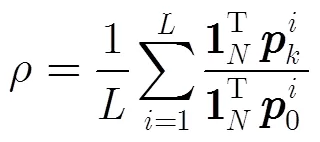
总的来说，图4的结果表明，文献[9]提出的算法能很好地应用于工作频率较低的MSRS，对于高频段工作的MSRS，该算法可能会因模型失配导致性能下降。在相同条件下，置信水平越高，目标的跟踪精度越低。图4(a)的结果表明，文献[9]提出的功率分配算法的跟踪性能要明显优于基于NCCP的功率分配算法。这是因为UHF波段的雷达工作频率较低，目标的反射系数起伏比较平缓，与文献[9]假设的一阶Markov转移模型匹配，因此目标的跟踪精度较高；而基于NCCP的功率分配算法则没有利用目标RCS预测模型的信息，只是根据历史观测数据，在统计意义下获取了一组最优的分配结果，是一种较为保守的算法。由于目标RCS的起伏程度会随着雷达工作频率的提升而加剧，文献[9]假设的一阶Markov转移模型与S波段的RCS起伏情况不再匹配(如图2(b)所示)。在这种模型失配的情况下，各个时刻预测的目标RCS将会与真实值出现较大的偏差。然而，由图2(b)可知，在大多数时刻，目标对雷达2和雷达3的反射系数最高。虽然预测结果与真实值有偏差，但预测结果仍满足目标对雷达2和雷达3的反射系数较高这一条件。换句话说，MSRS仍将大部分功率资源分配给这两部目标反射系数较高的雷达，因此整个算法的性能不会出现恶化，仍优于本文提出的较为保守的算法；在第16~22帧，目标对所有雷达的发射系数都比较小，这时目标的跟踪性能急剧下降(如图4(b)所示)。在第3种RCS模型下，文献[9]的算法已经无法正确地预测目标RCS，也不清楚下一时刻目标对哪部雷达的反射系数较高。在这种情况下，系统的功率资源可能分配给下一时刻反射系数很低的雷达，进而使算法性能恶化，而本文算法依然能保持较高的跟踪精度，由此验证了算法的鲁棒性。

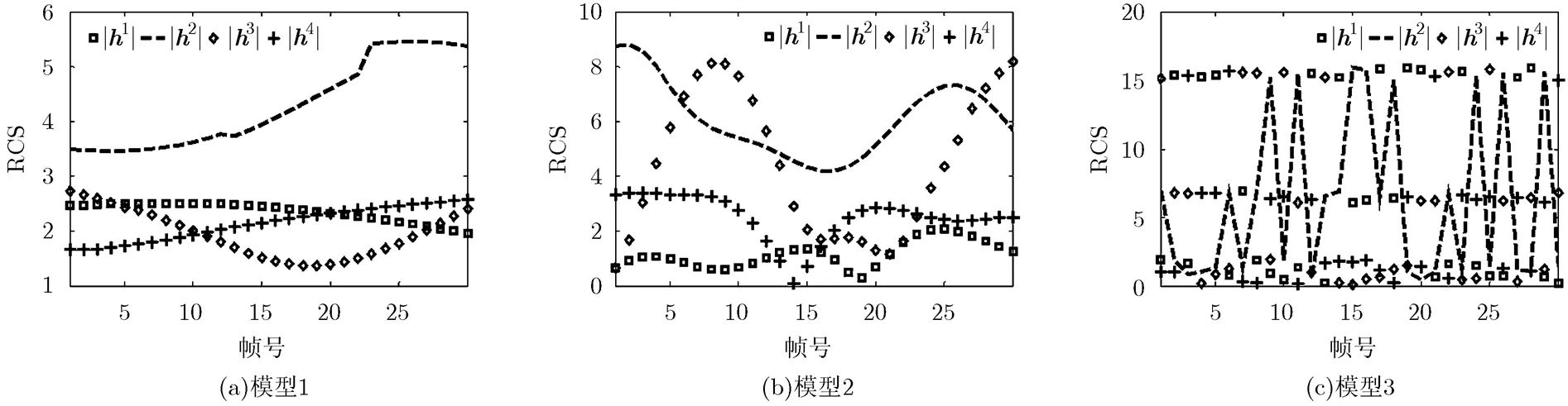
图2 3种不同的RCS模型

图3不同的RCS模型下的功率节省率

5 结束语

本文在MSRS平台下，提出了一种基于 NCCP模型的稳健功率分配算法，目的是使MSRS能动态地协调各部雷达的发射参数，进而在满足机会约束的条件下，尽可能地节约功率资源。该算法将目标的RCS建模为随机变量，采用NCCP模型进行分析，克服了现有算法强制将目标RCS的转移模型设定为一阶Markov过程而导致的模型失配问题，使功率分配算法更具鲁棒性。仿真实验表明，相对于均匀分配的情况，基于NCCP的功率分配算法能有效节约MSRS的功率资源。扩展实验表明：相对于文献[9]的算法，本文提出的资源分配算法对任何波段工作的MSRS都比较稳健。从实用性出发，下一步我们的研究工作将是改进NCCP模型的求解方法，使算法满足实时性的需求。

[1] 周万幸, 吴鸣亚, 胡明春. 双(多)基地雷达系统[M]. 北京：电子工业出版社, 2011: 1-30.

[2] 程院兵, 顾红, 苏卫民. 一种新的双基地MIMO雷达快速多目标定位算法[J]. 电子与信息学报, 2012, 34(2): 312-317.

Cheng Yuan-bing, Gu Hong, and Su Wei-min. A new method for fast multi-target localization in bistatic MIMO radar[J].&2012, 34(2): 312-317.

[3] 严俊坤, 戴奉周, 秦童, 等. 一种针对目标三维跟踪的多基地雷达系统功率分配算法[J]. 电子与信息学报, 2013, 35(4): 901-907.

Yan Jun-kun, Dai Feng-zhou, Qin Tong,.. A power allocation approach for 3D target tracking in multistatic radar systems[J].&2013, 35(4): 901-907.

[4] Godrich H, Petropulu A, and Poor H V. Resource allocation schemes for target localization in distributed multiple radar architectures[C]. Proceedings of Signal Processing, Aalborg, Denmark, 2010: 23-27.

[5] Godrich H, Petropulu A, and Poor H V. Power allocation strategies for target localization in distributed multiple-radar architecture[J].2011, 59(7): 3226-3240.

[6] Hero A O and Cochran D. Sensor management: past, present, and future[J]., 2011, 11(12): 3064-3075.

[7] Godrich H, Petropulu A, and Poor H V. Sensor selection in distributed multiple-radar architectures for localization: a knapsack problem formulation[J].2012, 60(1): 247-260.

[8] 丁鹭飞, 耿富录. 雷达原理[M]. 第3版, 西安: 西安电子科技大学出版社, 2002: 141-169.

[9] Chavali P and Nehorai A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking[J].2012, 60(2): 715-729.

[10] Hong L J, Yang Y, and Zhang L. Sequential convex approximations to joint chance constrained programs: a Monte Carlo approach[J]., 2011, 59(3): 617-630.

[11] Liu Y F and Song E. Sample approximation-based deflation approaches for chance SINR constrained joint power and admission control[OL].http://arxiv.org/abs/1302.5973, 2013.

[12] 李可维, 柳彬, 徐正喜, 等. 基于机会约束规划的无线Mesh网跨层优化算法[J]. 计算机应用研究, 2012, 29(6): 2306-2309.

Li Ke-wei, Liu Bin, Xu Zheng-xi,.. Cross-layer optimization algorithm for wireless Mesh networks based on chance constrained programming [J].2012, 29(6): 2306-2309.

[13] Wendt M, Li P, and Wozny G. Nonlinear chance-constrained process optimization under uncertainty[J].&, 2002, 41(15): 3621-3629.

[14] Sun H, Xu H, and Wang Y. Asymptotic analysis of sample average approximation for stochastic optimization problems with joint chance constraints via conditional value at risk and difference of convex functions[J]., 2012, 154(2): 1-28.

[15] Pagnoncelli B K, Ahmed S, and Shapiro A. Sample average approximation method for chance constrained programming: theory and applications[J].2009, 142(2): 399-416.

[16] Ristic B, Arulampalam S, and Gordon N. Beyond the Kalman Filter: Particle Filters for Tracking Applications[M]. Boston, MA: Artech House, 2004: 1-82.

[17] Van TreesH L. Detection, Estimation, and Modulation Theory, Part III[M]. New York, NY: John Wiley and Sons, 1971:275-352.

[18] Nemirovski A and Shapiro A. Convex approximations of chance constrained programs[J]., 2006, 17(4): 969-996.

[19] Sawik B. Conditional Value-at-Risk vs. Value-at-Risk to multi-objective portfolio optimization[J]., 2012, 15(13): 277-305.

严俊坤： 男，1987年生，博士生，研究方向为认知雷达、目标跟踪与定位、协同探测.

刘宏伟： 男，1971年生，博士，教授，博士生导师，主要研究方向为雷达系统、雷达信号处理、雷达自动目标识别等.

戴奉周： 男，1978年生，博士，副教授，研究方向为统计与自适应信号处理及其在雷达信号处理和目标检测中的应用.

罗 涛： 男，1983年生，博士生，研究方向为认知雷达、MIMO雷达发射波形设计、稳健接收波束形成.

保 铮： 男，1927年生，教授，博士生导师，中国科学院院士，主要研究方向为雷达信号处理和现代信号处理等.

Nonlinear Chance Constrained Programming Based Robust Power Allocation Algorithm for Multistatic Radar Systems

Yan Jun-kun Liu Hong-wei Dai Feng-zhou Luo Tao Bao Zheng

(,,’710071)

Almost all the existing works on power allocation assume that the target Radar Cross Section (RCS) information is known a priori. In order to deal with the uncertainty of the target RCS, a robust power allocation algorithm for MultiStatic Radar Systems (MSRS) is proposed based on Nonlinear Chance Constrained Programming (NCCP), in which the target RCS is modeled as a random variable with unknown distribution. Firstly, the Bayesian Cramer Rao Lower Bound (BCRLB) is derived. Then, the NCCP model is built with the objective of minimizing the total transmit power of MSRS, while the BCRLB outage probability is enforced to be greater than a specified probability. The resulting stochastic optimization issue is solved via Conditional Value at Risk (CVaR) relaxation and Sample Average Approximation (SAA) method. Finally, the validityand robustness of the proposed algorithm are verified with the simulation results.

MultiStatic Radar Systems (MSRS); Power allocation; Chance Constrained Programming (CCP)

TN953+.7

A

1009-5896(2014)03-0509-07

10.3724/SP.J.1146.2013.00656

2013-05-10收到，2013-10-12改回

国家自然科学基金(61201285, 61271291)，新世纪优秀人才支持计划(NCET-09-0630)和全国优秀博士学位论文作者专项资金(FANEDD-201156)资助课题

严俊坤 jkyan@stu.xidian.edu.cn