小学生数学学习差距研究
——教师视角:以中美教师对退位减法的认识为例
陈六一
(阳山实验小学校 江苏 苏州 215151)
一、引言
2013年12月3日,PISA2012在全球65个国家和地区同步揭晓评比结果,第二次参加该项目测评的上海学生再次登上“世界第一”。接着2014年上半年,英国教育大臣、芬兰教育代表团相继来上海“取经”。这激起了笔者对小学生数学成就的研究兴趣,于是翻阅TIMSS的研究成果,并结合自己数次亲历的美国小学数学课堂,发现中国,乃至受中国文化影响的新加坡、日本、韩国等国家和中国台湾地区的小学生,数学成绩一直远远超过美国。IEA研究者们认为产生这种差距的原因主要有以下几种:文化背景的差异,比如家长的期望,“数·词”体系;小学体制,学习数学的时间;数学教学内容及其安排。[1]可是,通过观察美国的小学数学课堂,以及与美国同行的交流,发现“学习差距”不仅仅局限于学生。换句话说,也就是教师对数学知识的认识,直接影响着数学的教与学。
访谈以退位减法为例,请看这几个题目:

你会怎样教学生做这样的题目?你觉得学生在学习退位减法之前,需要具备怎样的数学知识和数学技能?
二、美国小学数学教师的数学认识
1.知识理解——注重计算程序
A教师:42-7,学生要知道不能从2中直接减去7,那么就要从十位上借一个10来,所借的1,它等于10,如果把4划掉,把它变成30,现在就是12-7=5,那么左边就剩下3,把它挪下来。
B教师:不能从较小的数中减去较大的数,学生必须从邻位中借,因为邻位中有更多。打个比方就是,如果你没有足够的个位数,你可以到朋友那里去借,朋友那儿有许多。
32位美国教师的问卷,有26位(81.25%)关注计算程序。这些小学数学教师希望他们的学生学会如何执行两个特别的步骤:从十位上拿1个10来,然后把它换成10个1;并把“拿”这个步骤称之为“借数”。根据“所借的1等于10”的现实,他们解释第二个步骤为“变”。从这里可以看出他们对教学法的理解:一旦学生能够正确执行这两个关键步骤,就能正确地完成整个计算。
有5位(15.63%)教师如C、D老师所述,则期望他们的学生不仅仅学会计算过程,也要学会运算法则蕴含的数学基本原理。这些方法强调:在“拿”的背后是重组,在“变”的背后是转换。
C教师:学生必须理解42的意思……我会出示数字42,以及3个十和12个一,等于42。我会在两者之间进行比较,因为在你重组时知道的不是那么多,必须理解的是重组部分。一开始就是这个重组。
D教师:学生必须理解如何进行转换。可利用10进制的积木玩具,得到一个具体的数:10,例如按十进制,在个位上,10个1和1个10是相等的。学生要习惯于在位值内部进行转换,即实际的值不发生变化,但是进行了转换。
教师期望学生所知道的,其实与教师自己的知识理解相关。一如前文的26位教师,仅仅希望学生学会计算过程,这样学生收获的往往也就只是过程性的理解。何况“不能从较小的数中减去较大的数”是一个错误的断论。尽管低年级的学生还没有学习如何从较小的数中减去较大的数,但这并不意味着数学上没有这个事实。这个高级的技能不要求在低年级教学,可也不能因为强调了错误观念而引起学生将来学习的混乱。
把被减数中的两个阿拉伯数字比作邻居或朋友,是另一种数学上的误导,这暗示了被减数中的两个阿拉伯数字是独立的两个数,而不是一个数的两个部分。
再者,“借数”的解释暗含着又一个错误:在计算中数的值不一定要保持不变,而是可以任意改变——如果一个数太小了,由于某种原因需要增大一些,就可以从另一个数那里“借”一定的值来。
E教师:你们认为,从42中,能否拿出一个数字27?如果可以,那么用2减去7,我们做得到吗?这儿是2,我直观地表示出 1,拿走 7,1,2。不够。那么我们能做什么呢?我们可以到这个数的另一个部分,拿我们能用的东西,即从另一边取来,拿到我们需要帮助的个位,让2变成12。
而E教师则排除了上面说的那些错误理解,在E教师的阐释中,42-27不是独立的两个过程:2-7,40-20。计算是一个有机的整体:“从四十几中,拿走二十几。”不是“不能从较小的数中减去较大的数”,而是低年级学生的数学现实理解:“可以到这个数的另一个部分,拿我们能用的东西。”注意:“这个数的另一个部分”和“另一个数”,所表达的数学意义有着质的区别。但是,这样的数学知识理解,只占了问卷总数的3.12%。
2.教学策略:为操作而操作
教学42-27=?[2]
学生操作1:
(1)摆4链(每链10个回形针)和2个回形针在桌上,把其中一链拆开,成3链与12个。
(2)取走2链与7个回形针。
(3)数一数,剩下多少个,并且决定剩下的要排成一链加5个或是15个。
学生操作2:
(1)摆4链和2个回形针在桌上。
(2)再摆2链与7个回形针在桌上。
(3)为了使42个与27能互相配合计算,42里面要有一链被拆散。
(4)拆散42中的一链,回形针成为3链与12个。
(5)两组对齐后,各取走7个单独的回形针。
(6)两组对齐后,各取走2链回形针。
(7)数一数,罗拉比金吉多了一链加5个即15个回形针。
学生操作3:
(1)摆4链和2个回形针在桌上。
(2)摆2链和7个回形针在桌上。
(3)为了使42能与27个配合,42里面的一链必须拆散。
(4)拆散42中的一链,成3链12个。
(5)将两组中的链和单个的回形针配对。
(6)数一数,克拉蒂还需要一链加5个或单独15个回形针。
很明显,美国教学案例中学生通过具体的学具操作,既获得了运算的意义,辅以大量的时间,又保证儿童寻找到自己的解,并在学具操作中完成计算。如同美国同行们的解读:“通过参与性的经验活动,操作性工具会比仅仅讲述能更好地促进学习。”然而,好的交通工具不一定能保证到达正确的目的地。因为学者们已经注意到,为了促进对数学的理解,教师有必要帮助学生把操作性工具和数学思想之间的联系清晰地表达出来。
所以教师要适当组织教学:“如果把1个链子打开,将会发生什么?我们会有多少个1?用哪种方式可以进行减法?”乃至追问:“你们现在告诉我,你有没有在42上填什么或者去掉什么?4个10和2个1,与3个10、12个1是相同的,那么当你从中取走27个时会发生什么?”
三、中国小学数学教师的数学认识
1.知识分析——退一法
赵老师:我会告诉学生,当你在计算42-27这样的问题时,首先要把数字排列起来,从个位开始减起。因为要从2中减去7不够减,应该从十位退1个10来把它变成10个1。再把这1个10加到个位就得12;用12-7=5;然后转到十位,由于十位上的4已经借走1个10给个位,所以只剩下3个10,用3-2=1,把它放在十位上。
赵老师的解释和美国的A、B教师相似,注重的是运算法则的具体步骤,没有显示出对原理的关注。但中国教师持有这种计算程序性取向的比率,比美国要小得多,如图1所示。不过,中国教师都会运用一个做减法重组的特定词语:“退一”。
钱老师:我会从一个直截了当的减法开始,如42-21=?在学生解决这个问题后,我把问题变成42-27=?这个问题与第一个问题的不同点在哪里?在计算新问题时会发生什么?学生很快会发现7比2大,没有足够的个位数去减。见机我会说好,但有时我们个位数太多了,你们应该记得上周我们利用进位做加法,那时我们做了什么?学生会说“满十进一”。我接着说,那么当我们没有足够的个位数去减时怎么办?可以从十位退一。如果把40中的一个十退位了,会发生什么?用这种方式我就会引入“退1成为低位上的10”。
孙老师:要在42中减去7,没有足够的个位数怎么办?42显然大于7。42中的个位数在哪里?学生会说42中的其他个位数被组合成十位数了。然后我会问我们可以做些什么,得到足够的个位数字来减去7。通过回忆,学生会有分解一个10的想法。
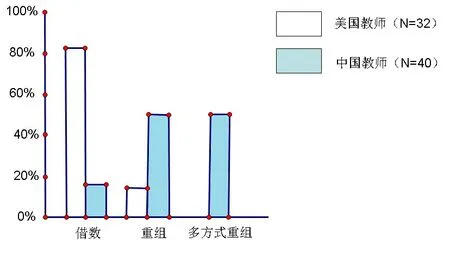
图1 教师对于利用重组做退位减法的理解
把“拿”的步骤描述为“退一”,比“重组”的解释更全面。因为在使用“退一”的概念时,减法过程是以一种表明了它与加法运算的关联方式来阐述的,这不仅为减法学习提供更多的表征支持,而且强化了学生之前的学习。而且,中国教师除了像美国教师注重“重组”那样强调1个10由10个1组成,近一半的中国教师还提到了一个重组数字前的一个概念:进率。这些教师主张:学生应该清楚“1个10里有多少个1”和“百位与十位、十位与个位的进率是多少”的答案一致。
形如把42拆成30和12,是所有美国教师的标准方式,无人超越这个方式。但是,不乏有中国教师指出,这不是进行减法计算的唯一正确途径,围绕着“退一”原理,教师们讨论了各种各样的重组方式。
李老师:42-27=30+10+2-20-7=(10-7+2)+(30-20)=15。这种方式的好处在于从10中减去7比从12中减去7容易些,而且这个程序中所包含的加法不涉及进位,所以非常简单。
周老师:42-27=42-2-5-20=40-5-20=35-20=15。这样把27拆成20、2、5三个数值,那么42-2不用退位,40-5和35-10与学生思维都是很简单。
2.教学策略:系列水平动作
教学42-27=?
[教师出示4捆小棒(每捆10根)和2根小棒]
师:这些小棒表示几?
生:42。
师:要从42里去掉27,就是42减27(板书:42-27=?),个位上够减吗?
生:不够减。
师:个位上不够减,怎么办?请小朋友拿出小棒,动动脑筋,想想办法,个位上怎么减去7呢?
(学生操作,教师巡视。)
师:现在老师请小朋友来汇报一下,你想出了什么好办法?
(在学生回答的同时教师示范操作。)
师:个位不够减7,从4捆小棒中取出1捆,也就是从十位退1。十位上的1退到个位上是几?为什么?
生:是10,因为1个10是10个1。
师:个位上的2不够减7,从十位退1,在个位上加10再减。个位上10加2等于12,12减7等于5,个位上写5,十位上4退1还有3,3-2=1。所以42减27等于15。
(教师小结并板书:个位不够减,从十位退1,在个位上加10再减。)
其实,中国小学数学教师在教学“42-27”之前,已经把“20以内的减法”的教学,当作“退一”需要的减法重组概念过程基础。所以教学中,教师提出:“个位上不够减,怎么办?请小朋友拿出小棒,动动脑筋,想想办法,个位上怎么减去7呢?”学生的思维能快速聚焦“个位上的2不够减7,从十位退1,在个位上加10再减。”
也就是说,减法中的重组思想,把高位退一到低一位当十,是通过一系列的水平动作完成的。此案例教学之后就是被减数是三位数和更多位数,且新的水平动作又是连续的分解,比如208-15,203-18,1000-18。
在美国,诸如“9+3”“16-7”这样的问题,被认为是“基本的算术事实”,仅仅需要记忆即可。而在中国,概念的“种子”,早在第一个水平——“20以内的减法”就出现了。
同时观察课堂,尽管发现中国教师用到教具、学具的频率比美国教师少,但他们认为操作了,就要像课例中就活动操作要进行必要的讨论、报告、展示、辩论,如上文中所述,“现在老师请小朋友来汇报一下,你想出了什么好办法?”再例如吴老师谈了他在开学之初的一次教学讨论,又在学期结束进行了思辨。
吴老师:计算42-27,利用教学具的时候,学生是从高位开始的,先从42中拿去20,再拿去7。这如同日常生活,付10元钱买了3元6角的东西,我们先减3元,再减6角。从学生的数学现实经验来看,学校里的正式数学学习似乎更加复杂,而且意义更少。当我们在本子上演算就会发现,从十位开始的话,我们在十位上先得到一个差2,然后转到个位上,我们就又要改变刚刚所得到的差。如果我们一开始从个位开始计算,这个麻烦就可以避免了。然而这种解释只能解决一半的问题——用竖式计算为什么从个位算起。由于学生还没有看出这种标准算法的明显好处,我建议他们保留疑惑。期末,再次讨论时,学生们很快发现,在遇到更大的数的时候,标准方式对绝大多数问题而言,优势更加突出。
如果吴老师的数学认识与教学策略,仅是停留在为操作而操作阶段,那么很难想象他会引导学生达到这样的数学理解。
四、结论及讨论
问卷、访谈与课堂观察的结果,揭示了教师们对于小学数学教学内容所拥有的知识不够充足,美国教师为甚。以退位减法为例,81.25%的美国小学数学教师和17.50%的中国小学教师,只拥有计算程序性知识,他们的理解仅仅局限于运算法则的表面——拿和换的步骤。正是这种数学认识的局限性,限制了他们在课堂中促进学生概念性学习的能力。
虽然操作教学具,是小学数学课堂教学的一种重要手段,但决定学生的学习质量,还是要依赖于教师认为学生应该学会的概念。与美国教师形成鲜明对照的是,绝大多数中国教师在活动操作之后,会进行班级讨论,这个教学策略使得学生的数学学习能得以同化与顺应,使得新旧知识得以平衡,不是为了操作而操作。
通过退位减法的问卷与访谈,教师所呈现的数学认识模型,有一元单项表述,也有多元系列水平动作。结合课堂教学观察,系列水平动作的教学更符合布鲁纳的研究:“掌握某一学科的结构以理解这个学科,可以使许多其他事物与该学科有意义地联系起来。简而言之,学习结构就是学习事物是如何关联的。”[3]诚如布翁所言,教师若能够把数学系列水平的概念种子放入到阶段教学中,不仅能促进现在的数学知识表征,而且“大量的迁移是可以实现的,甚至可以达到如此程度,即在适宜条件下恰当地学习可以使人‘学会怎样学习’,这确实是事实。”[4]▲
[1]马立平.小学数学的掌握和教学[M].李士锜,吴颖康,等,译.上海:华东师范大学出版社,2013:19.
[2]Marjorie J W.创意教学策略[M].吕金燮,译.台北:洪叶文化事业有限公司,1998:207-230.
[3][4]Jerome Bruner.布鲁纳教育文化观[M].宋文里,黄小鹏,译.北京:首都师范大学出版社,北京:2011:24,25.

