软弱岩体双连拱隧道施工力学响应分析

周 亮

(湖南省湘西公路桥梁建设有限公司，湖南 吉首 416000)

0 引言

虽然连拱隧道引入我国较晚，其以占地少，影响公路线性小等优点在公路、市政道路中广泛应用［1］，近年来，我国修建较多的大跨度双连拱隧道，如起初修建的广州白云山隧道，跨度较大，达31.5 m，还有沪蓉高速公路冯家垭口隧道、福泉高速公路相思岭隧道、云南大保高速公路元磨隧道等。

双连拱隧道由于施工工序复杂，跨度大，施工时中隔墙、衬砌及围岩等结构受力状态复杂，受力情况随开挖过程频繁变化，这给施工安全带来较大困难，如何保证施工及运营过程中中隔墙、衬砌及围岩的稳定，是工程研究的重点。特别是当隧道通过破碎、结构松散的全风化、强风化岩体时，施工过程中的围岩及支护结构受力将更加复杂，中隔墙、衬砌、拱腰及拱脚等部位的受力将显著加大，中隔墙反复出现偏心受压，影响隧道整体稳定性，研究隧道施工过程中的力学行为是保证施工安全的关键［2，3］。

双连拱隧道的施工方法很多，主要有中导洞、侧壁导洞法、多步施工法等，本文以某采用侧壁导洞法施工的双连拱隧道为背景，通过建立数值计算模型，模拟隧道开挖及支护过程，并计算了各施工步下的围岩、中隔墙等的力学响应，并分析隧道围岩的稳定性，可为类似工程提供参考。

1 隧道概况及设计参数

本连拱隧道为双向6 车道，单洞路面净宽12.5 m，净高8.0 m，隧道全长220 m，进出口桩号分别为K21+125、K21+345，隧道处于正常下坡路段，没有超高，纵坡坡度1.3%，隧道最大埋深14.8 m，最小埋深5.7 m，属于浅埋隧道。

根据设计阶段的地质勘察报告，隧道长度范围内围岩分级均Ⅵ级，进出口段围岩破碎情况更为严重，本次数值计算选取进口段桩号为K21+148 断面进行数值模拟计算。

根据本隧道的具体设计情况，隧道支护采用复合式衬砌，根据施工图设计文件，隧道设计的总体原则是按新奥法原理设计的，以锚杆、喷射混凝土、钢筋网、钢架组成初期支护的联合支护体系，以模板砌筑钢筋混凝土作为二次衬砌。具体设计参数为:初期支护，格栅钢架间距0.75 m，Φ6 钢筋网20 cm ×20 cm，Φ25 锚杆，长 4.0 m，间距 1.0 m ×1.0 m，喷射C25 早强混凝土，厚度0.3 m;二次衬砌为模筑钢筋混凝土，标号C30，洞周厚度均为0.6 m。

本隧道采用侧壁导洞法进行开挖施工，具体施工工序如下(见图1):

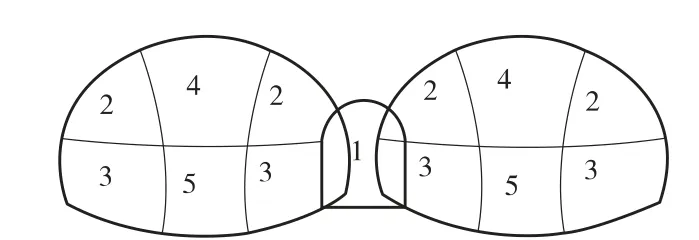
图1 侧壁导洞法施工步图

中导洞开挖、支护，中隔墙浇筑，中导洞回填→两侧导洞内外侧上半部分开挖及支护→两侧导洞内外侧下半部分开挖、支护→中部上半断面的开挖及支护(中部预留岩土体)→左右洞室中部预留岩土体的开挖→左右洞中部下半部分开挖及支护→拆除临时支护→隧道左右洞进行二次衬砌。

2 计算模型及参数

2.1 计算模型

一般情况下，可根据隧道围岩地质条件、开挖面积及地应力场水平等影响因素来选取计算影响范围，本次计算采用试算的方式确定模型大小，以避免边界条件对二维有限元计算的影响，试算结果表明，当隧道左右侧模型范围大于40 m 时，左右边界对计算结果没有影响;当隧道底部模型范围大于20 m时，底部边界对计算结果无影响。因此，最后选定模型范围为水平宽度为130 m，竖直高度为42。确立取值根据地质资料，本隧道穿越区段岩土层主要包括人工填土、全风化砂岩、强风化砂岩。计算模型采用三角形单元，上部边界采用自由边界，底部水平、竖直方向均约束，两侧边界仅水平方向约束。

计算程序通过设置对应的施工步来模拟施工中的隧道开挖过程，并模拟施加锚杆、衬砌等支护对隧道围岩的影响，以期达到模拟隧道开挖、支护施工全过程的目的［4～6］。模型计算网格划分图如图2。

图2 模型计算网格划分图

2.2 计算参数

本次计算中，计算材料采用的弹塑性(平面应变)本构模型、D －P 屈服准则。隧道围岩、中隔墙砌筑体、中隔墙回填采用实体单元模拟，施加的锚杆和初衬采用板单元模拟，而二次衬砌则采用梁单元模拟，在初衬和二衬之间的接触面上设置了接触面单元，共划分了 5 138 个单元［7～9］。由地质勘查报告及设计文件提供的参数，计算中使用的各种材料的物理、力学参数见表1。

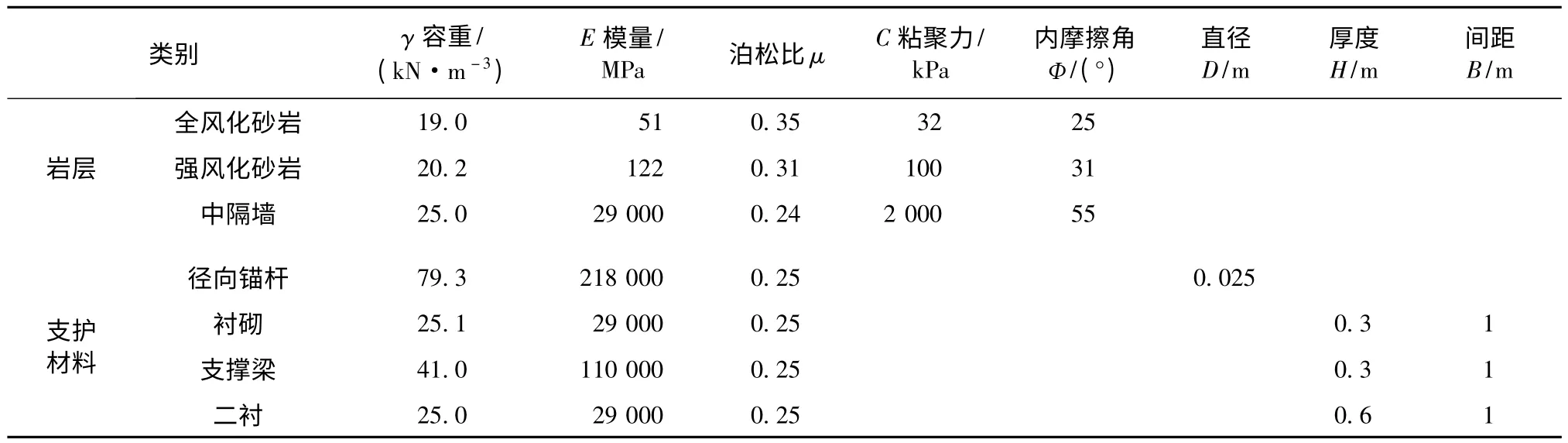
表1 材料物理力学参数

3 计算结果及分析

3.1 两侧导洞内外侧上半部分开挖及支护［10］

建立上述模型后，当进行两侧导洞内外侧上半部分开挖及支护后，得到的围岩、中隔墙的数值应力及塑性区如图3所示。

由图可知，左右洞拱腰及开挖导洞的下方角落处出现了应力集中，左洞拱腰处大小为－531 kPa，直角处为－536 kPa，应力集中的范围都较小，呈点状区域，围岩其余位置竖直应力未出现集中现象。中隔墙竖直应力最大处发生在中下部以及下部角隅处左右侧(表面侧)位置，左侧最大竖直应力大小为－304 kPa，右侧对应位置为－303 kPa，中隔墙两侧的竖直应力最大值基本相同，但从图中可看出，左侧的应力区要略大于右侧，其余位置竖直应力对称分布。围岩塑性区主要出现左右洞拱腰处，中隔墙左右侧墙中部也分布有较大范围的塑性区。

图3 两侧导洞内外侧上半部分开挖及支护后围岩、中隔墙竖直应力及塑性区分布

3.2 两侧导洞内外侧下半部分开挖、支护

当进行两侧导洞内外侧下半部分开挖、支护后，得到的围岩、中隔墙的数值应力及塑性区如图4所示。

图4 两侧导洞内外侧下半部分开挖、支护后围岩、中隔墙竖直应力及塑性区分布

由图可知，左右洞拱腰处、拱脚处的竖直应力集中现象有明显改善，这些竖直应力的大小有小幅度的增加，左洞拱腰处大小为－589 kPa，右洞拱腰处为－592 kPa，整体来看，开挖面附近围岩竖直应力均有所增大。对比左右洞围岩竖直应力分布可知，其基本以路线中线轴对称分布。中隔墙竖直应力较上一施工开挖步有较大幅度的增长，左侧最大竖直应力发生在左侧下部角隅处，大小为－1 177 kPa，较上一施工步增大287.2%，右侧角隅处未见明显的应力集中，最大竖直应力发生在中部截面最小处，大小为－882 kPa，较上一施工步增大191.1%。可以看出虽然中隔墙竖直应力有所增大，但大小依然在设计范围内，整个中隔墙未出现拉应力，说明其整体受力状态较好。

拱腰处的塑性区分布有所增大，中导洞侧墙墙角处出现小面积的塑性区分布，此外，左右洞中部未开挖断面的中下部均出现较大范围的塑性区分布，这主要是因为，该区域为下一阶段开挖区域未进行初期支护，围岩在开挖临空后，在竖直应力重分布且增大后，进入屈服状态，形成了较大范围的塑性区。这种塑性区应分两种情况分析:①若塑性区迅速发展，且位移量测有突变现象时，应进行必要的临时支护，避免产生坍塌，影响隧道施工安全;②若塑性区分布虽然较大，前一施工步完成后未继续发展，且位移测量数据收敛时，可不进行特殊处理，因为本断面即为下一阶段开挖断面。

3.3 中部上半断面的开挖及支护(中部预留岩土体)

当进行中部上半断面的开挖及支护后，得到的围岩、中隔墙的数值应力及塑性区如图5所示。

由图可知，中部上半断面的开挖及支护后，隧道洞周及中隔墙的竖直应力继续增长，左洞拱腰处最大竖直应力为－741 kPa，较上一施工步增长25.8%，右洞拱脚最大竖直应力为－744 kPa。左右洞拱顶与上一开挖步交界点处出现了应力集中，但竖直应力绝对值不大，为－395 kPa，此外中导洞侧墙墙角处应力集中现象有所发展，范围增大，最大竖直应力也有较大幅度的增长，大小为－833 kPa，两侧对称分布。对比左右洞围岩竖直应力分布可知，其基本以路线中线轴对称分布。中隔墙竖直应力较上一施工开挖步继续增长，左侧最大竖直应力发生在左侧下部角隅处，大小为－1 383 kPa，较上一施工步增大17.5%，最大竖直应力发生位置与上一施工步相同，右侧角隅处未见明显的应力集中，最大竖直应力发生在中部截面最小处，大小为－1 079 kPa，较上一施工步增大22.3%。可以看出虽然中隔墙竖直应力有所增大，但其数值大小依然在设计范围内，整个中隔墙未出现拉应力，说明其整体受力状态依然较好。

本开挖步后，左右洞拱腰处的塑性区分布未见明显变化，中导洞侧墙墙角处的塑性区范围继续发展扩大，这与应力发展规律相同，此外，中导洞两侧拱腰也出现了塑性区，整体来看，塑性区分布范围基本以路线中线对称分布。

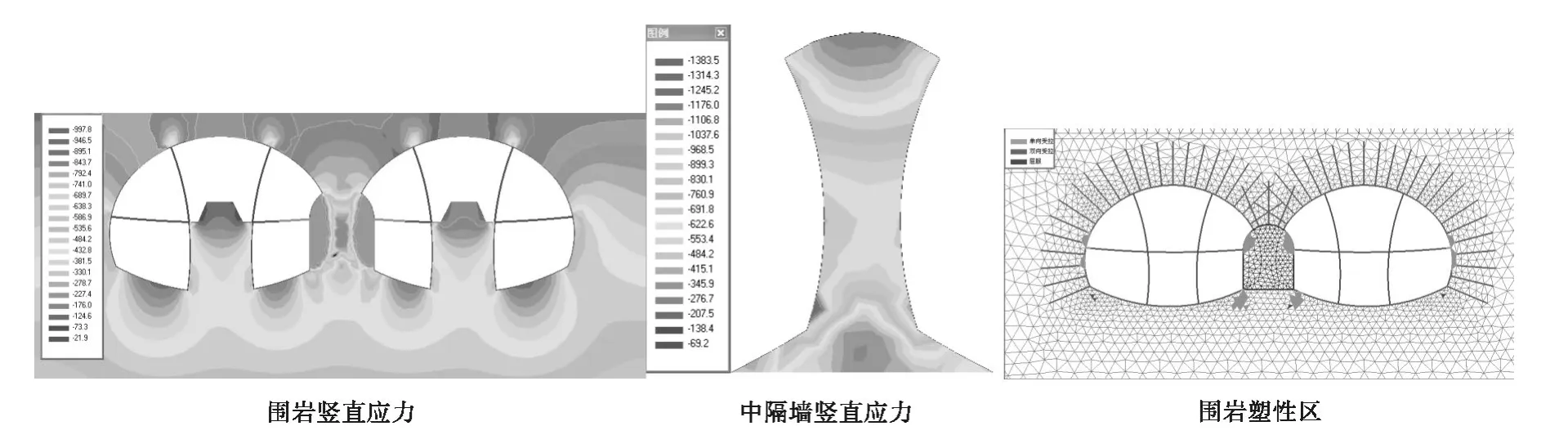
图5 中部上半断面的开挖及支护后围岩、中隔墙竖直应力及塑性区分布

3.4 拆除临时支护并施加二衬

当完成拆除临时支护并施加二衬后，得到的围岩、中隔墙的数值应力及塑性区如图6所示。

图6 拆除临时支护并施加二衬后围岩、中隔墙竖直应力及塑性区分布

由图可知，完成拆除临时支护并施加二衬后，隧道围岩应力重新分布，隧道洞周及中隔墙的竖直应力均有所增加。左右洞围岩基本对称分布，拱腰、拱脚处的应力集中现象得到缓解，左洞拱腰处竖直应力大小为－991 kPa，右洞拱腰处竖直应力大小为－987 kPa，数值应力增大主要是因为初期支护拆除后，围岩应力重分布引起的。

中隔墙竖直应力也有所增大，其最大竖直应力分布在中隔墙左右侧下部的角隅处(表面侧)，大小为－3 155 kPa。中隔墙左侧中部最大竖直应力为－2 830 kPa，右侧中部最大竖直应力为－2 821 kPa，左右侧仍存在较小的偏压，但幅度非常小，在可承受范围内。其余部位的竖直应力基本呈对称分布，大小均有所增大，其原因与围岩应力增大一样，都是因为临时支护拆除导致应力重分布所致。

左右洞塑性区分布范围基本对称，左右两侧拱腰至拱脚的塑性区范围有所减小，但中隔墙下部岩体出现了与中隔墙成45°角对称分布的塑性区，其产生的原因为中隔墙作为主要载体承担上部岩体的重力，并将其传递至其下岩体，导致下部岩体应力增大引起塑性屈服。

支护结构受力情况见图7和图8所示。

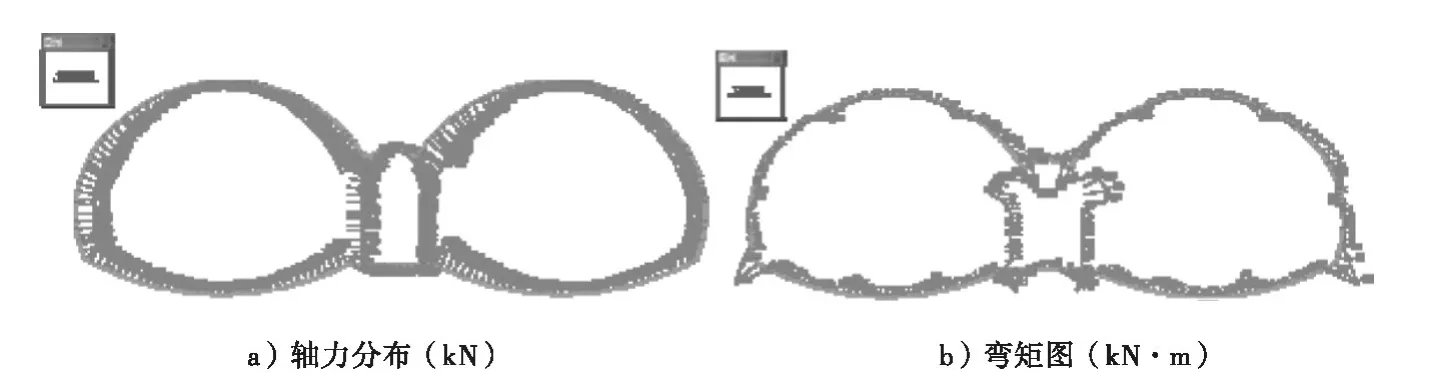
图7 初衬受力情况

由此可知，初期支护轴力均为正，说明初衬处于受压状态，没有出现拉应力，最小轴力出现在拱顶，仰拱中部轴力也较小，拱腰处轴力最大。最大弯矩也出现在拱脚处，初衬的轴力和弯矩基本呈对称分布，大小均在材料的强度范围内。二衬的轴力和弯矩与初衬有相同的分布规律，轴力均为正，二衬也都处于受压状态，较大轴力和弯矩均分布于拱脚处，内侧靠近中隔墙处的拱脚轴力最大。由于隧道断面对称开挖，左右洞室轴力、弯矩基本都呈对称分布。

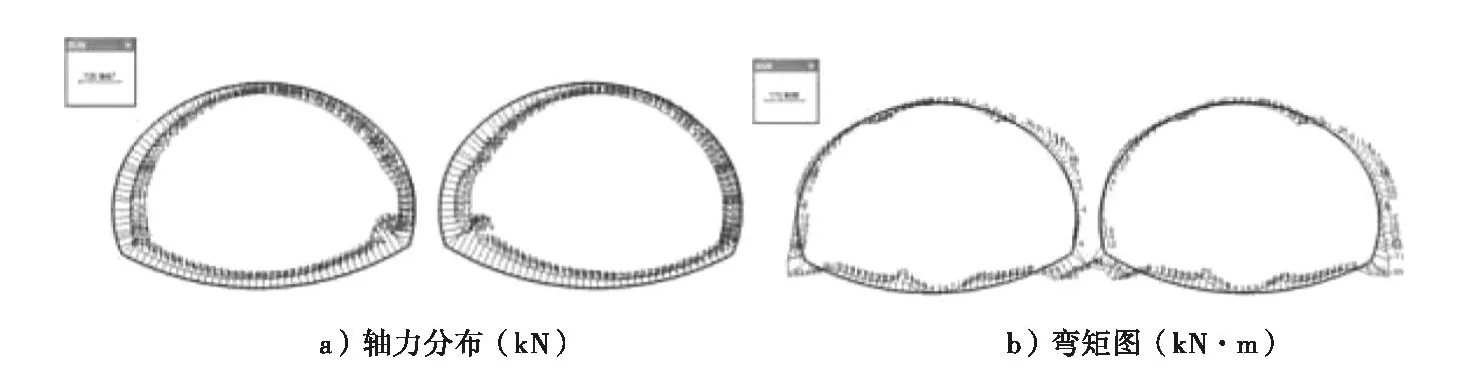
图8 二衬受力情况

4 结语

本文对软弱岩体双连拱隧道施工力学行为进行了数值模拟计算，并对隧道开挖支护全过程进行了计算分析，得到如下结论:

1)隧道断面对称开挖时，隧道围岩、中隔墙及衬砌支护的受力基本对称分布，避免了围岩偏压以及中隔墙的偏心受压，利于隧道施工稳定。

2)两侧导洞内外侧下半部分开挖、支护后，左右洞中部未开挖断面的中下部均出现较大范围的塑性区分布，此处临空面较大，施工中这是一个容易产生破坏的区域，特别是在松散的软岩体中，若位移量测数据不收敛时，应对该区域进行必要的临时支护(注浆、锚杆或钢支撑支护)，避免发生坍塌，影响隧道施工安全。

3)拆除临时支护后，左右洞室围岩应力、中隔墙最大竖直应力均处于最大值，此步骤应全面测量拱顶、拱腰及地表等变形数据，并绘制相应曲线，做好沉降预测分析，并及早地施加二衬，确保围岩稳定。

［1］蒋树屏，胡学兵.云南扁平状大断面公路隧道施工力学相应数值模拟［J］.岩土工程学报，2004，26(2).

［2］吴俊强，刘永华，李 围.浅埋偏压连拱公路隧道施工数值模拟分析［J］.公路交通科技，2005(4).

［3］王 勇，徐干成，乔春生.公路隧道数值模拟分析及衬砌安全性评价［J］.现代隧道技术，2004(S).

［4］刘 涛，沈明荣.连拱隧道动态施工模型试验与三维数值仿真模拟研究［J］.岩石力学与工程学报，2006，25(9).

［5］潘昌实.隧道力学数值方法［M］.北京:中国铁道出版社，1995.

［6］邓 建，朱合华，丁文其.不等跨连拱隧道施工全过程的有限元模拟［J］.岩土力学，2004，25(3).

［7］刘劲勇.连拱隧道围岩与支护结构稳定性研究［D］.武汉:武汉理工大学，2005.

［8］董学晟.水工岩石力学［M］.北京:中国水利水电出版社，2004.

［9］高 谦，乔 兰.地下工程系统分析与设计［M］.北京:中国建筑工业出版社，2005.

［10］李 军.大跨度公路隧道动态施工围岩稳定性数值分析［D］.南京:河海大学，2006.