基于ExtendSim 的VSI 均值控制图改进方法

周 万，张 莹

(武汉理工大学 物流工程学院，湖北 武汉430063)

在实际生产活动中，最常用的控制图是产品计量特性服从正态分布的固定抽样区间(fixed sampling intervals，FSI)均值控制图。可变抽样区间(variable sampling intervals，VSI)均值控制图是对FSI 均值图的一种改进，它试图采用可变的抽样区间来减少控制图报警所需要的时间，通过理论计算可以证明VSI 均值图的工作性能优于FSI 均值图［1-2］。

FSI 均值图将μ -3σ 设置为控制下限(lower control line，LCL)、μ+3σ 设置为控制上限(upper control line，UCL)、μ 设置为中心线(center line，CL)。VSI 均值控制图除了具有LCL、CL、UCL 3条线之外，还增加了下警戒线(lower warning line，LWL)和上警戒线(upper warning lin，UWL)。LWL=μ0-k'σ0，UWL=μ0+k'σ0，如图1 所示，d1对应的区域为警戒域，样本均值落在该区域时，使用短抽样区间d1抽取下一个样本，d2对应的区域为中心域，样本均值落在该区域时，使用长抽样区间d2抽取下一个样本，样本均值落在最上和最下两块区域时，控制图报警，停止生产过程。

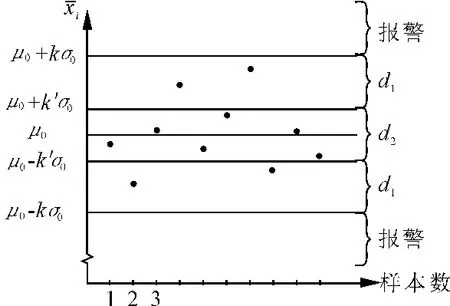
图1 VSI 均值控制图

在VSI 均值图的研究方面，郭宝才等［3-4］对FSI 及VSI 均值图的性能进行了研究，指出VSI 均值图比FSI 均值图具有更好的工作性能;张斌等［5］研究了VSI 均值图的优化设计问题;ZHANG等［6］研究了参数未知的正态分布VSI 均值图，得到了不同参数条件下VSI 均值图的工作性能指标;MAHADIK［7］研究了具有可变样本容量、可变抽样区间，以及警戒线(variable sample size，sampling interval，and warning limits，VSSIWL)的均值图，并将其与VSSI(variable sample size，sampling interval)均值图，以及VSSI(1，3)均值图的工作性能进行比较，计算结果发现，合适的参数选择对于VSSIWL 均值图的工作性能非常重要，在多数情况下，VSSIWL 的工作性能介于VSSI 与VSSI(1，3)之间。上述研究主要通过理论计算对VSI 均值图进行研究，采用理论推导的方式对控制图工作性能进行改进。相对于FSI 均值图，通过上述研究方法得到的VSI 均值图在工作性能方面的优势不够明显，控制图工作性能的改进程度较小。因此，通过采用理论推导与仿真实验相结合的方法，对VSI 均值图的抽样过程进行模拟和改进，得到了改进的VSI 均值图，仿真实验表明，该方法能够有效改进VSI 均值图的工作性能。

1 FSI 和VSI 均值图性能指标的计算

设生产过程处于受控状态时产品总体的计量特性服从正态分布N(μ0，σ)，在抽取第一个样本时生产过程已经发生异常，总体均值μ0发生了偏移，偏移量为δ = |μ0-μ1|/σ0，δ 在0 ～2 之间取值，以0.1 为步长逐渐增长。当生产过程异常时，计量特性服从正态分布N(μ0+δσ0，σ)。假设每个样本的样本容量为m，则样本均值服从正态分布N(μ0+δσ0，σ20/m)。产品总体均值发生偏移使得被抽取的样本落在上下控制限之外的概率变大，并且均值偏移量δ 越大，样本落在控制限之外的概率越大。

在比较各种控制图的好坏时，平均链长(average run length，ARL)和平均报警时间(average time to signal，ATS)是很重要的指标，通常的做法是固定二者的可控ARL 或ATS，之后比较失控ARL 或ATS，失控ARL 或ATS 越小的控制图的检测能力越好［8］。由于FSI 均值图的ARL 与ATS相等，VSI 均值图的ARL 与ATS 不相等，通过控制FSI 与VSI 均值图在受控状态时拥有相同的报警所需平均样本数［9］(average number of sample to signal，ANSS)，比较二者失控状态下的ARL 或ATS，ARL 或ATS 越小，则控制图工作性能越好。

设p为样本均值落在控制限之外的概率，则：

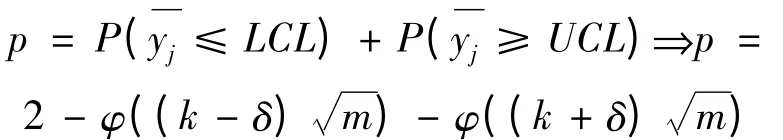
其中，0 ＜k'＜k。当样本均值落在警戒域时，使用较小的抽样区间d1作为抽取下一个样本的抽样间隔;当样本均值落在中心域时，使用较大的抽样区间d2作为下一个样本的抽样间隔。由图1 可知，警戒域和中心域的范围主要由k'决定，而控制限的大小则由k决定。在比较FSI 和VSI 均值图的工作性能时，需要使二者的ANSS 相一致。ATS 及报警时间标准差(standard deviation of time to signal，SDTS)的计算公式如下［10］：

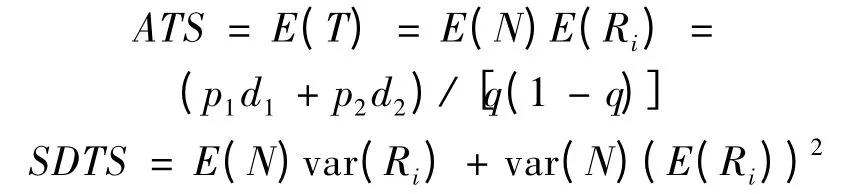
其中，p1为使用短抽样区间的概率，p2为使用长抽样区间的概率。由以上公式可以计算出VSI 均值控制图的ATS 和SDTS 的理论值，如表1所示。为了使VSI 均值图在μ =μ0时具有与FSI均值图相同的ANSS 和ATS，对于选定的d1和d2，可以利用下式计算k'的值，从而确定中心域和警戒域范围。

FSI 均值图的ARL、SDRL 以及VSI 均值图的ATS、SDTS 的理论值如表1 所示，VSI 均值图所采用控制图参数为d1=0.1、d2=1.9、m=5。

2 ExtendSim 仿真实验结果

ExtendSim 仿真软件由美国Imagine That 公司采用C 语言开发，可以对离散事件系统和连续系统进行仿真，具有较高的灵活性和可扩展性［11］。利用ExtendSim 可以对FSI 均值图和VSI均值图的抽样过程进行仿真。仿真模型通过5 个Random 模块随机生成一次取样中5 个产品的不同观测值，这5 个产品的计量特性服从相同参数的正态分布。通过Equation 模块求5 个观测值的均值，并将该值赋给Resource Item 的一个资源，设定Resource Item 有且仅有一个资源。Create 模块每隔1 个时间单位生成一个Item，表示抽取一个样本。设定每次试验的运行时间为2 000 个时间单位，运行次数为400 次，利用Set，Get 以及Decision 等模块实现重复抽样与结束抽样等过程。最后利用与Exit 相连的Mean＆Variance 模块对输出的结果进行跨轮次统计分析，实验结果中的“均值”为ARL 实验值，“标准差”为SDRL 实验值。Mean＆Variance 模块选择“重复到相对误差小于0.05 为止”来实现统计的精度要求，这种情况下模型的运行次数通常会大于400 次。VSI 均值图的仿真模型如图2 所示，模型利用4 个Decision 模块判别样本均值落在警戒域还是中心域。FSI 均值图和VSI 均值图相关性能指标的仿真结果如表1 中的实验值所示。

通过计算理论值与实验值的相对误差发现，在所有均值偏移量下，FSI 均值图的理论值和实验值一致性良好，ARL 的相对误差均在0. 03 以下，SDRL 的相对误差均在0.05 以下。当均值偏移量在0.5 以下时，VSI 均值图的ATS 理论值和实际值的一致性良好，相对误差率很小，分别为0.004、0.007、0.001、0.009、0.021 和0.021，随着均值偏移量逐渐增大，相对误差率逐渐变大，一致性逐渐变差。当均值偏移量较大时，实验值比理论值少了0.1 个时间单位。通过分析，发现误差产生的原因在于第一个样本应该在何时抽取，仿真实验所模拟的抽样过程是在生产过程刚开始时就抽取第一个样本，当样本值超出控制限时，立即停止生产过程。而理论计算基于的抽样过程是第一个样本必须在第一个抽样区间之后抽取，且第一个抽样区间是在长短抽样区间之中随机抽取的。由于仿真实验所模拟的VSI 抽样过程更符合生产实际的操作习惯，因此其结果更具有指导意义。

表1 两种均值控制图性能指标的理论值和实验值

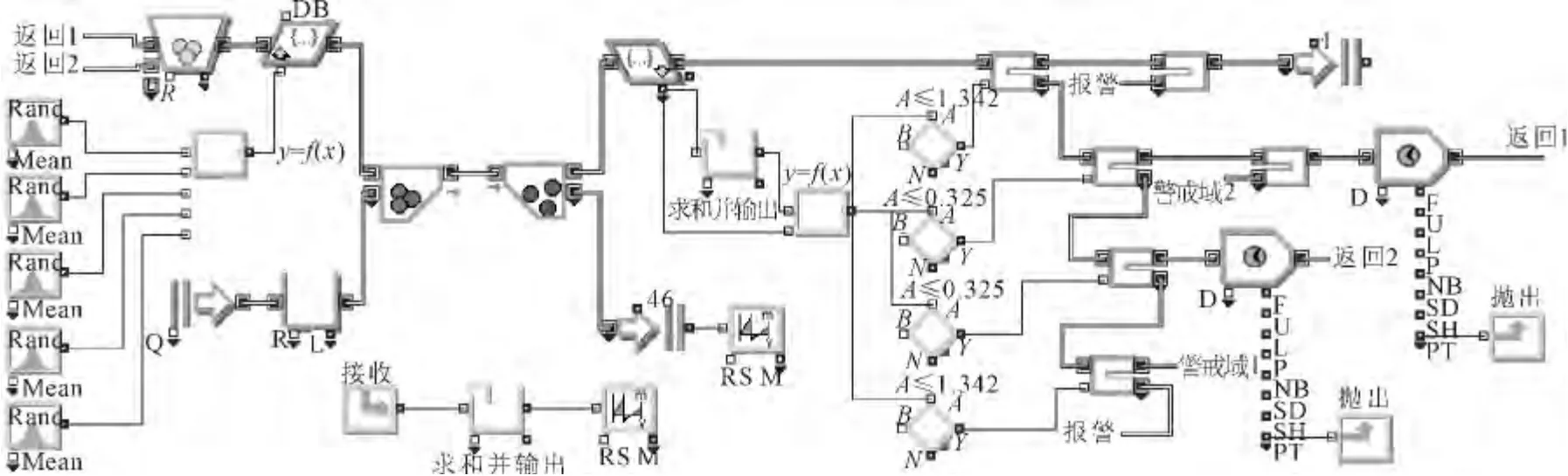
图2 VSI 均值图的仿真模型

3 IVSI 均值控制图的ExtendSim 仿真实验

相对于FSI 均值图而言，VSI 均值图在ATS和SDTS 指标上有所改进，但改进程度不明显，并且相对于ATS，SDTS 的值过大，在数值上基本与ATS 相等，这说明在不同的抽样试验中，报警时间的波动非常大。为了使VSI 均值图对于小的均值偏移反应更加灵敏，需要对VSI 均值图加以改进，笔者将讨论一种基于ExtendSim 的改进VSI(improved variable sampling intervals，IVSI)均值图，该IVSI 均值图对于较小的均值偏移拥有明显减小的ATS 和SDTS，因而具有更好的工作性能。

产品计量特性服从正态分布，通过简单变换可转化为标准正态分布。设计量特性服从正态分布，x～N(μ0，σ20)，则(x-μ0)/σ0～N(0，1)。对于标准正态分布，样本均值的期望为0，利用ExtendSim 考察标准正态分布样本均值累积求和的特性，比较当δ 分别为0 和0.1 时的样本均值累积和随抽样过程的变化情况，当δ =0 时，样本均值的累积和趋向于围绕y=0 上下波动，而当δ =0.1 时，样本均值的累积和趋向于围绕某条直线y=kx上下波动，如图3 所示。利用标准正态分布样本均值累积和这一特性，可以对VSI 均值图加以改进，从而使得新的IVSI 均值图对于较小的均值偏移量反应更为灵敏。新的IVSI仿真模型应该满足以下两个条件：①当均值偏移量δ =0时，IVSI 均值图的ATS 值应该不小于VSI 均值图的ATS，并且IVSI 均值图的ANSS 值应该小于或大致等于VSI 均值图的ANSS。②当均值偏移量δ≠0 时，IVSI 均值图的ATS 值应该小于VSI 均值图的ATS，并且IVSI 均值图的SDTS 值应该小于VSI 均值图的SDTS，此外IVSI 均值图的ANSS 值应该小于或大致等于VSI 均值图的ANSS。

IVSI 的仿真模型如图4 所示。

图3 样本均值累积和仿真结果界面图

图4 IVSI 均值控制图抽样过程仿真模型

为了使IVSI 均值图满足要求，在仿真模型中添加一个Holding Tank 模块用于实现样本均值的累积求和。通过比较当前样本均值的大小，选择较大的作为决定下一个抽样区间取值的判别值。在IVSI 仿真模型中，长短抽样区间分别选取0.1 和1.9。为了使IVSI 满足条件①，必须适当弱化样本均值累积和在IVSI 均值控制图中的作用，这是因为当δ=0 时，样本均值累积和很有可能超出控制限，使控制图过早报警，将样本均值累积和除以一个合适的整数可以达到这个目的。利用Equation 模块比较的大小，选择较大的用于Decision 模块的判别是为了保证IVSI 均值图的ANSS 与VSI 均值图的ANSS 相匹配，因为ANSS 代表了抽样代价。

对比表1 中的IVSI 实验值与VSI 实验值，可以发现：

(1)当均值偏移量δ =0 时，IVSI 均值图的ATS 和ANSS 值与VSI 均值图的相应指标吻合，说明笔者的IVSI 仿真模型符合条件①的要求。

(2)当均值偏移量δ≠0 时，对于较小的均值偏移，IVSI 均值图的ATS 和SDTS 值明显低于VSI 均值图，说明对于较小的均值偏移量IVSI 模型比VSI 模型具有更高的灵敏性，并且报警时间的标准差更小。当均值偏移量较大时，IVSI 均值控制图的ATS 值比VSI 均值控制图的稍大，但由于δ 较大时的ATS 本身已经很小，加上两者的差距不明显，因而对控制图的工作性能影响不大。此外，在ANSS 性能指标上，由于IVSI 均值图比VSI 均值图使用了更少的样本，因此IVSI 均值图基本上满足了条件②的所有要求。图5 分析了IVSI 与VSI 均值图在0 ≤δ ≤1.0 时 的ATS 及SDTS。当均值偏移量δ 较小时，IVSI 均值图的ATS 值大约为VSI 均值图的1/2;IVSI 均值图的SDTS 比ATS 明显小，而VSI 均值图的SDTS 与ATS 基本一致，这说明IVSI 均值图相对于VSI 均值图有了很大改进。

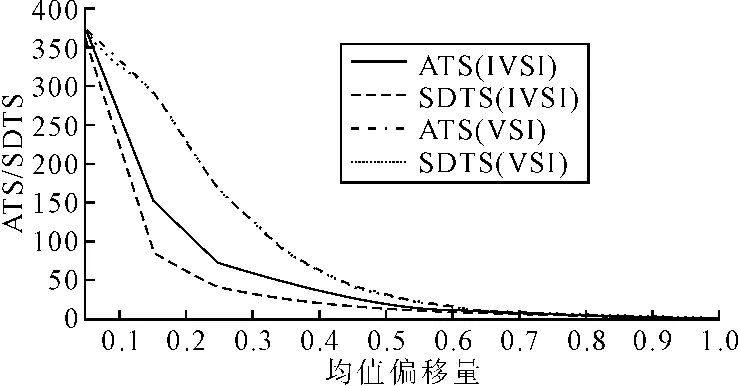
图5 IVSI 及VSI 均值图的性能指标对比

对比文献［6］关于VSI 均值图ATS 及SDTS的理论计算值，发现笔者的理论计算值与文献［6］的计算结果(d1=0.1、d2=1.9、m=5 时)一致。将文献［6］中相关的理论计算值(偏移量δ=0.2)与笔者提出的IVSI 均值图的实验值进行比较，如图6 和图7 所示。图6 为ATS 指标的比较，图7 为SDTS 指标的比较，从左至右7 个组别采用的长短抽样区间依次为(0. 5，1. 5)、(0. 3，1.7)、(0.1，1.9)、(0.1，1.1)、(0.1，1.3)、(0.1，1.5)、(0.1，4.0)，图中任意一个点代表一组特定的控制图参数。最下方直线代表IVSI 均值图的仿真实验值，其工作比所有参数下的VSI 均值图好(所有的点均落在直线上方)，因此笔者提出的IVSI 均值图比一般VSI 均值图更加有效。

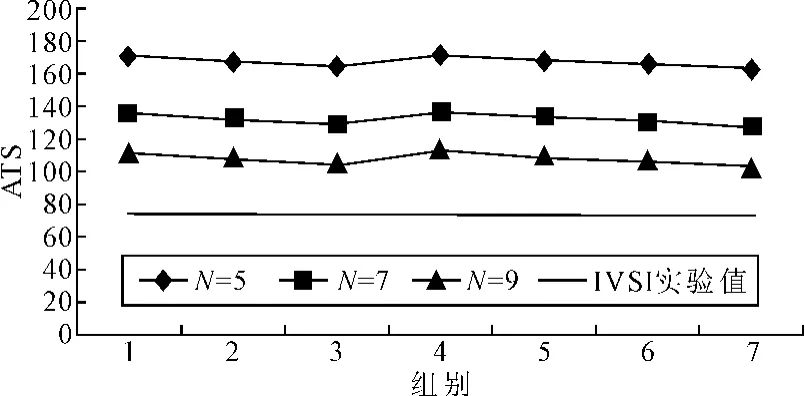
图6 ATS 指标对照

4 结论

笔者利用ExtendSim 仿真软件建立了FSI、VSI 均值图抽样过程的仿真模型，并将仿真模型的运行结果与理论计算值进行对比分析，发现FSI 仿真模型的运行结果与理论计算值具有较高的一致性，VSI 仿真模型的运行结果在均值偏移量较小时与计算值具有较高的一致性，当均值偏移量较大时一致性较差。通过对VSI 仿真模型实验结果与理论计算值之间的误差进行分析，发现VSI 仿真模型模拟的抽样过程更加符合实际生产的操作习惯，因而其实验结果对于实际生产更加具有指导意义。通过对VSI 均值图抽样过程的分析，建立了一种基于ExtendSim 的IVSI 均值图抽样模型。仿真实验结果表明，该IVSI 均值图相对于一般VSI 均值图具有更好的工作性能，这种基于仿真实验的优化方法为VSI 均值图的参数设计提供了一种新思路。

图7 SDTS 指标对照

［1］郭宝才.可变抽样区间均值图的优化［J］.统计与决策，2007(23)：22 -23.

［2］郭宝才，孙利荣. 可变抽样区间均值图的改进方法［J］.统计与决策，2008(5)：22 -23.

［3］郭宝才，孙利荣. 可变抽样区间图［J］. 杭州师范大学学报：自然科学版，2009，8(1)：6 -9.

［4］郭宝才，孙利荣.随机飘移下变抽样区间图的设计［J］.系统管理学报，2010，19(1)：89 -92.

［5］张斌，周伟灿，费文龙.可变抽样区间图的优化设计［J］.统计与决策，2010(21)：17 -20.

［6］ZHANG Y，CASTAGLIOLA P，WU Z，et al. The variable sampling intervalchart with estimated parameters［J］. Quality and Reliability Engineering International，2012，28(1)：19-34.

［7］MAHADIK S B.charts with variable sample size，sampling interval，and warning limits［J］. Quality and Reliability Engineering International，2013，29(4)：535 -544.

［8］王兆军，巩震，邹长亮.ARL 计算方法综述［J］.数理统计与管理，2011，30(3)：467 -495.

［9］王兆军. 关于动态质量控制图的设计理论［J］. 应用概率统计，2002，18(3)：316 -333.

［10］REYNOLDS M J，AMIN R W，ARNOLD J C，et al.X bar charts with variable sampling intervals［J］.Technomotrics，1988，30(2)：181 -192.

［11］秦天保，王岩峰. 面向应用的仿真建模与分析［M］.北京：清华大学出版社，2011：65 -90.