关于二元函数可微的充分条件证明过程的探讨

韩晓艳

（青岛工学院基础教育学院，山东 青岛 266300）

关于二元函数可微的充分条件证明过程的探讨

韩晓艳

（青岛工学院基础教育学院，山东 青岛 266300）

关于二元函数全微分存在的充分条件给予不同的证明过程，在高等数学的教材中一般都利用拉格朗日中值定理证明，本文主要利用无穷小与极限的关系予以证明，并且可以得出较弱的充分条件.

极限；无穷小；中值定理；可微

0 引言

可微定义如下：

如果函数z=f（x,y）在点（x0,y0）的全增量可表示为其中A、B不依赖于△x、△y而仅与x0,y0有关，，则称函数z=f（x,y）在点（x0,y0）可微分.

可微的充分条件（见［2］中P21定理2）.

如果函数z=f（x,y）的偏导数fx（x,y）、fy（x,y）在点（x0,y0）连续，则函数在该点可微分.

1 预备知识

引理1无穷小与函数极限的关系（见［1］中定理）.

2 主要结论

定理如果函数z=f（x,y）至少有一个偏导数不妨设fx（x,y）（或fy（x,y）在点（x0,y0）连续，则函数在该点可微分.

证考察函数的全增量

在第一个方括号内的表达式，

应用无穷小与极限的关系，得到

又依条件fx（x,y）在点（x0,y0）连续，得

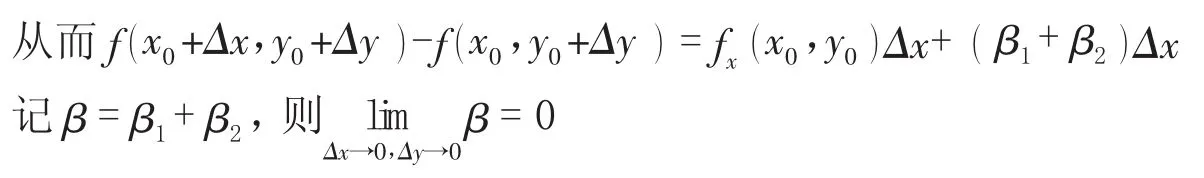
由此可见，在一个偏导数fx（x,y）连续的假设下，全增量△z可以表示为

这就证明了z=f（x,y）在点（x0,y0）可微.

［1］同济大学应用数学系.高等数学上册［M］.北京：高等教育出版社，2006.

［2］同济大学应用数学系.高等数学下册［M］.北京：高等教育出版社，2006.

（编辑 郭继荣）

O174

A

1673-1808（2014）03-0022-02

2014-03-17

韩晓艳（1982-），女，山西榆次人，青岛工学院基础教育学院，讲师，硕士，研究方向：运筹与控制论.