混合系数线性模型参数可容性估计的小样本分析

殷月

(锦州师范高等专科学校，辽宁 锦州121000)

0 引言

混合系数线性模型一般形容:

Z(t)=［x(t)］'α+［y(t)］'β

其中，x(t)=(x1(t)，…，xp(t))';y(t)=(y1(t)，…，yq(t))';x1(t)，…，xp(t)，y1(t)，…，yq(t)都是t的已知函数。α 是p×1 的固定系数向量，β 是q×1 的随机系数向量，且有β～(b，Σ)。若对m 个样品分别在ti1＜… ＜tini(i=1，2，…m)时刻进行检测，得到如下数据:

Zij=［x(tij)］'α+［y(tij)］'βi+εij，i=1，2，…，m;j=1，2，…，nini＞p+q

这里βi和εij分别是每个样品的随机系数和每次测量的误差，且相互独立(0，σ2)，若

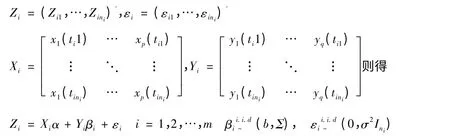
其中:p ≥0，q ≥0;当p=0 时时模型化为完全随机系数的形式，当q=0 时模型化为一般的线性模型。这里还要求Rank(Xi)=p，Rank(Yi)=q，那么

Rank(Xi，Yi)≤p+q

若设Ci=(Xi，Yi)，d=(a'，b')'，ei=Yi(βi－ b)+εi，则Zij=［x(tij)］'α+［y(tij)］'βi+εij，i=1，2，…，m;j=1，2，…，nini＞p+q 式为

Zi=文献［1，2］已经研究了一些混合系数线性模型的参数估计。在本文中，我们将研究可估向量Sd 在线性估计类φ 中的可容性估计。其中设S 为各行向量为组成的n×(p+q)矩阵，显然S'=(s1，…，sn)。文献［3］中以得出若所有都可估，则向量Sd 可估。这里采用以下二次损失函数和矩阵损失函数

其中A 为n×n 矩阵，AY 为Sd 的某线性估计，d=(α'，b')' 为p+q 维参数向量。如果在损失函数(1)或(2)之下AY 相对于线性估计类φ 为Sd 的可容许估计，则记为AY～Sd。

1 可估参数向量Sd 的可容许估计

一般的线性模型

其中σ2＞0 未知，V ＞0 已知，Y 为n×1 的观测向量，X 为n×p 的已知设计阵。下面两个引理讨论中，S、A 分别为n×p 和n×n 矩阵。

引理1:模型(3)中，LY 是Sβ 的一个线性估计且L 和S 为常数阵，则一切β 及σ2＞0 有

当且仅当且等号成立的满足下列条件之一:

(1)L=LXT－X'V－1

(2)μ(VL')⊂μ(X)

这里T=X'V－1X。

参见文献［3］的第194 页引理4.7 的证明过程。

引理2:在二次损失之下若有AY～Sβ，则在矩阵损失下也有AY～Sβ。

参见文献［3］的第212 页引理4.10 的证明过程。

得到M ＞0 且已知，和以下定理。

定理1:混合系数线性模型Z=Cd+e，e～N(0，σ2M)，其中若Sd 可估，则当且仅当二次损失之下AZ～Sd 满足以下条件:

(1)A=ACT－C'M－1

(2)ACT－C'A' ≤ACT－S'

这里T=C'M－1C

证明:先来证明CT－C' 与CT－S' 与选取T－无关

又Sd 可估，则有S'=C'N' (其中的N 为某任意矩阵)，所以ACT－S'=ACT－C'N' 也与选取T－无关。可以得出CT－C' 与CT－S' 是唯一确定的。

这里指出条件(2)包含了的矩阵ACT－S' 为对称阵。

当Sd*=S(C'M－1C)－C'M－1Z=AZ 时，即A=S(C'M－1C)－C'M－1，则

又由

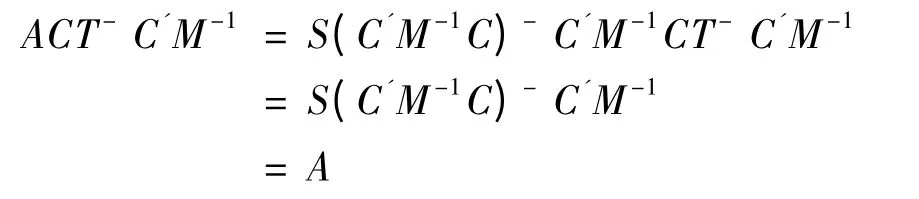
即定理1 中条件(1)成立。

又由于

即定理1 中条件(2)成立。于是有如下定理

定理2:在模型(3)中，Z=Cd+e，e～N(0，σ2M)，若Sd 可估，则在矩阵损失和二次损失下，若设d*=(C'M－1C)－C'M－1Z 则Sd*～Sd。

证明:先证明在线性估计类中Sd*是可估向量Sd 的可容性估计。由定理1，有AZ～Sd，再由式(5)得到在二次损失下Sd*～Sd。又由于引理2 可知矩阵损失下Sd*～Sd，

这里只需再证明Sd*的唯一性

当Sd 可估，有

S'=C'N' 即S=NC(N 为某适合矩阵)

则

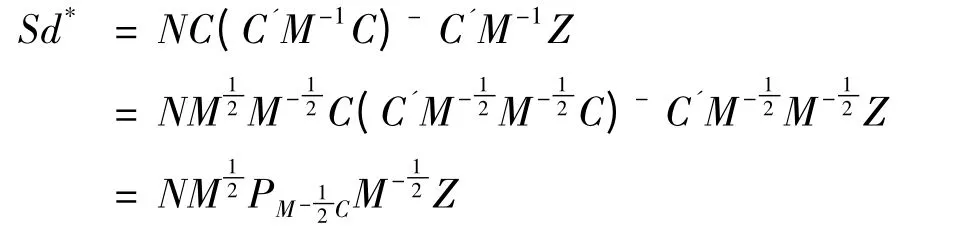
2 固定系数α 和随机系数期望β 的可容许估计

定理3:在模型(3)中，Z=Cd+e，e～N(0，σ2M)，当rk(C)=p+q 时，在矩阵损失和二次损失下，设=(C'M－1C)－1C'M－1Z 则～d。

在定理2 中，由于d 是可估向量，此时可取S=I，便可得到d*～d。若选取矩阵C 为列满秩阵，则

定理3 表明:在矩阵损失或二次损失下对于参数d=(α'，b')'，若在rk(C)=p+q 前提下，不可能寻求到线性估计类φ 中一个比有改善的估计。但在非线性估计类中是可能的。但这种非线性估计在使用上和应用上的合理性还需进一步论证，在以后相当长的时期内非线性估计可作为是热点讨论之一。

在混合系数线性模型(3)，Z=Cd+e，e～N(0，σ2M)。其中C=(X，Y)

d=(α'，b')' 在文献［4］中定理1 给出了固定系数α 和随机系数期望b 的一种无偏估计。α 的无偏估计为=(X'QX)－1X'QZ，b 的无偏估计为=(Y'PY)－1Y'PZ。这里P=M－1－ M－1X(X'M－1X)－1X'M－1，Q=M－1－ M－1Y(Y'M－1Y)－1Y'M－1。

定理4:在混合系数线性模型(3)中，当rk(C)=p+q 时，在二次损失(1)或矩阵损失(2)之下，～α，～b。其中采用D=diag(σ2M1，…，σ2Mm)=σ2(M1，…，Mm)=σ2M 的记法。和定义如上。

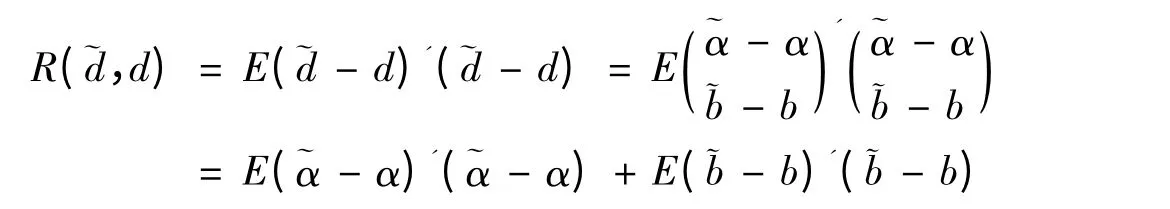
设参数d 的任意一个线性估计为LZ，这里L 为(p+q)×n 矩阵。同时L1为p×n 矩阵，L2为q×n 矩阵。可得参数α 和b 的任一无偏估计分别为L1Z、L2Z。二次损失(1)下，LZ 是参数d 的任意一个线性估计其风险函数如下

可得

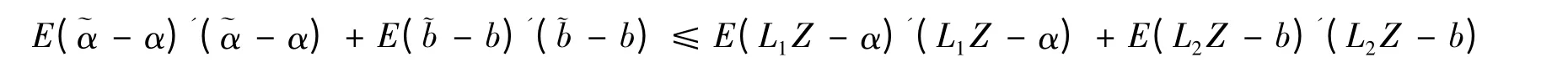
即

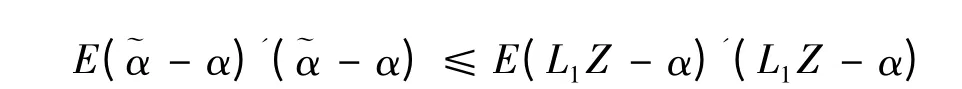
3 结 语

本文在二次损失和矩阵损失的条件下，给出了混合系数线性模型的可估参数向量Sd 在线性估计类中的可容许估计。当rk(C)=p+q 时，～d。并且针对固定系数α 和随机系数期望b 的无偏估计和，分别讨论了它们的可容许性。

［1］李辉，刘建州.混合系数线性模型中参数估计的一些结果［J］.吉首大学学报，2004，25(1):16－21.

［2］李辉.两种特殊线性模型的参数估计［D］.湘潭:湘潭大学硕士学位论文，2004.

［3］陈希孺，陈桂景.线性模型参数的估计理论［M］.北京:科学出版社，1985.