一类松籽、松鼠、幼苗的征税模型分析
郑洪艳,罗 勇,胡亦郑
(温州大学数学与信息科学学院,浙江温州 325035)
一类松籽、松鼠、幼苗的征税模型分析
郑洪艳,罗 勇†,胡亦郑
(温州大学数学与信息科学学院,浙江温州 325035)
运用微分方程理论,研究了一类非线性的红松种群征税模型,得到了该系统的平衡点,证明了该系统正平衡点的局部渐进稳定性和正平衡点的全局吸引域,利用Pontryagin最大值原理给出了最优征税策略.
数学模型;渐进稳定性;最优税收
长期以来,松籽、松鼠和幼苗之间相互影响、世代繁衍,并维持稳定,其中松籽和松鼠是具有较高经济价值的林副产品.为了科学开发和合理利用森林资源,从对该系统大量调查和直接观察到的现象分析得到,种子、鼠类(主要是指松鼠,同时也考虑花鼠、林姬鼠等)和幼苗是红松林发生和演替纽带,三者之间相互调节.
宋国华在文献[1]中研究了一类松籽、松鼠、幼苗的数学动态模型:
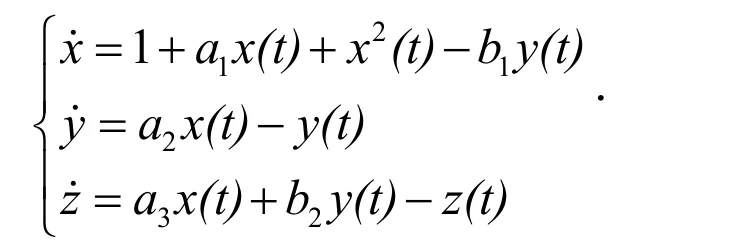
为了既能满足资源开发者的经济要求,又能更好的保护资源,人们在长期实践中寻找出了一种非常有效的资源收获策略,即对所开发的资源征一定的税.文献[2-6]分别研究了食饵-捕食征税模型,文献[7]研究了具有3阶段结构的自食单种群征税模型.本文研究了一类松籽、松鼠和幼苗征税系统,假设捕获的努力量是可变的,分析得出了该系统平衡点的存在性、局部性.通过研究生物经济平衡问题,指出了一个可行的生物经济平衡点与单位捕获强度的成本有关.
1 模型的建立
三条基本假设[1]:
1)不考虑其他因素时,松籽增长率按照理想的自发育过程不断增加,受松鼠影响不断减少;
2)松鼠增长率随种子数量增加而增加,随自身数量增加而减少(这里不考虑松鼠的年龄结构,认为它们的捕食与埋藏能力相同);
3)幼苗增长率随松籽数量增加而增加,随自身增加而减少.
我们考虑的模型如下:
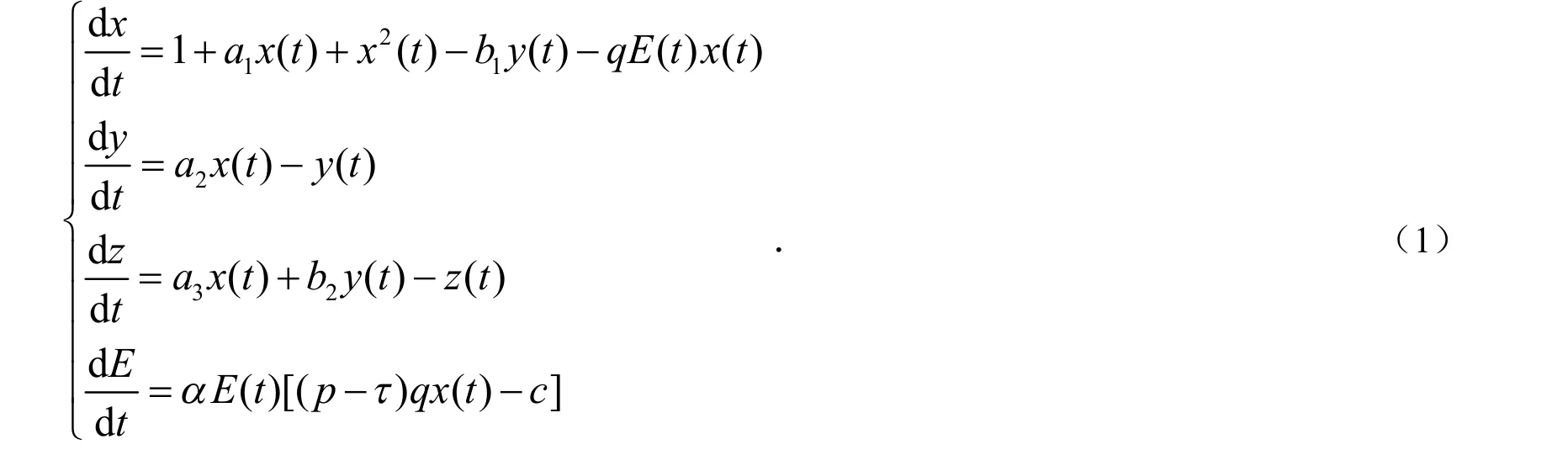

2 平衡点的存在性
情况I:当未对松籽征税(E=0)时,系统(1)可以变为:

情况II:当对松籽征税(E≠0)时,这时Y*是正平衡点,其中,x*,y*,z*,E*是以下方程组的正解:


3 平衡点的局部性质


4 平衡点的全局性质
定理3 假设条件(H2)成立,系统(1)的正平衡点Y*的吸引的吸引域为:


5 最优征税策略
为了使资源开发者在长期开发中获得的经济收益最大,我们将用最优控制理论控制捕获努力度,力求寻找一个最优的捕获努力量,在资源的长期开发中得到社会收入贴值为:
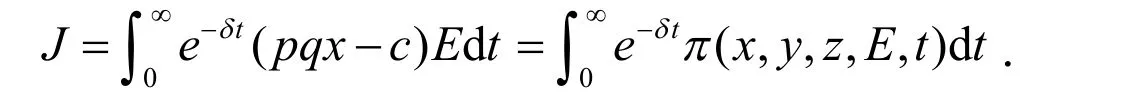
式中,δ为贴现率,e-δt为贴现因子.在满足状态方程(1)和控制约束条件τmin≤τ≤τmax下,希望能找到一个最优税收策略τ=τ(t),使J取得最大值.
首先,建立Hamilton函数:
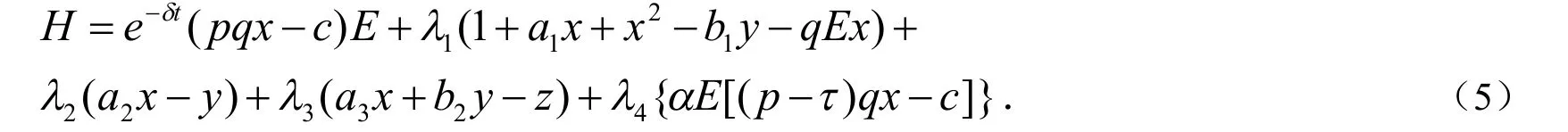
式中:λ1,λ2,λ3,λ4为伴随变量①Clark C W. Mathematical bioeconomic: the optimal management of renewable resources [M]. New York: John Whiley, 1990.,假设H必须在τ∈[τmin,τmax]中取得在最大值,上述问题的最优控制必是奇异控制与线性控制相结合,因此最优解不会在τ=τmin和τ=τmax上取得.
根据Pontryagin最大值原理,可得:

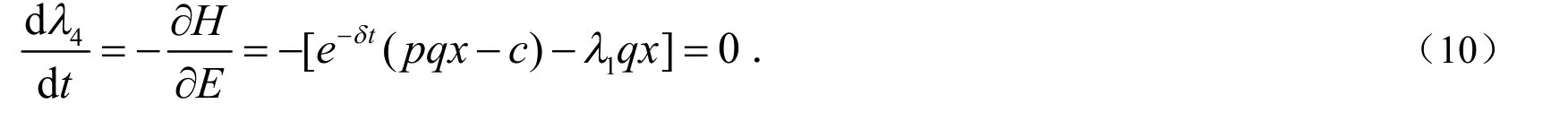
由(10)式得:

利用正平衡点所满足的状态方程,由(9)式得:

则线性微分方程组的解为:

式中A1=1-δ,A2=1.
同理由(8)式可得:

于是线性方程(14)的解为:

再由(7)式可得:

将(4)中得出的x*,y*,z*,E*值代入(16)式可得到一个关于τ的方程,设τδ为此方程的一个解(如果存在的话).再将τ=τδ代入x*,y*,z*,E*可得最优平衡解(x =xδ,y=yδ,z =zδ,E=Eδ).
通过以上分析,可得如下结论:
(1)从方程(6)、(13)、(15)和(17)中注意到λe-δt(i =1,2,3,4)(其中λ,i=1,2,3,4是伴随变量)在最优平衡解整个时间间隔内仍然不变.因此它们满足横截条件,例如当t→∞时它们仍有界.
6 结 论
本文研究了一类松籽、松鼠和幼苗征税模型,假设捕获的努力量是可变的,得到该模型平衡点的存在性以及局部性,利用Pontryagin最大值原理给出了最优平衡解.
[1] 宋国华, 李秀琴, 李俊清. 一类松籽、松鼠、幼苗的动态数学模型及讨论[J]. 生物数学学报, 1994, 9(4): 163-168.
[2] Ganguly S, Chaudhuri K S. Regulation of a single-species fishery by taxation [J]. Ecological Modeling, 1995, 82(1): 51-60.
[3] 张睿. 具有比率依赖型功能反应函数的食饵-捕食者征税模型分析[J]. 生物数学学报, 2008, 23(3): 484-488.
[4] 孙军芳, 荀晓侃, 张睿. 基于种群保护的最优税收策略[J]. 山东理工大学学报: 自然学科版, 2007, 21(5): 57-59.
[5] 贾春莹, 高建国. 具有比率的Holling III类功能性反应函数的捕食者-食饵征税模型分析[J]. 云南民族大学学报: 自然科学版, 2010, 19(3): 177-180.
[6] 贾春莹, 高建国. 改进了的捕食者-食饵系统的征税模型分析[J]. 数学的实践与认识, 2010, 40(16): 237-242.
[7] 曾夏萍, 高建国. 具有3阶段结构的自食单种群征税模型[J]. 宁夏大学学报: 自然科学版, 2012, 33(3): 233-237.
[8] Kar T K. Conservation of a fishery through optimal taxation: a dynamic reaction model [J]. Communications in nonlin-ear science and numerical simulation, 2005, 10(2): 121-131.
Analysis on Taxation Model of Pine Nut, Squirrel and Saplings
ZHENG Hongyan, LUO Yong, HU Yizheng
(Mathematics and Information Science College, Wenzhou University, Wenzhou, China 325035)
This paper studies a class of nonlinear taxation model of pine nut, squirrel and saplings by means of the theory of differential equations. The existence of the positive equilibrium of the system is discussed through the research. Locally asymptotic stability of the system’s positive equilibrium is proved and the attractive domain of the positive equilibrium is obtained. The problem of optimal taxation strategy is settled by taking the advantage of Pontryagin’s maximal principle.
Mathematical Model; Asymptotic Stability; Optimal Taxation
O193
A
1674-3563(2014)04-0001-07
10.3875/j.issn.1674-3563.2014.04.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:封毅)
2014-05-03
国家自然科学基金(11001204)
郑洪艳(1988- ),女,吉林长春人,硕士研究生,研究方向:生物数学.† 通讯作者,luoyong@wzu.edu.cn

