基于PLAXIS 2D堆载变化下深基坑支护结构性状研究
王 兴,计 亲,张克勋
(1.安徽建筑大学土木工程学院,安徽合肥 230601;2.温州大学建筑与土木工程学院,浙江温州 325035;3.铁道部第一勘测设计院,甘肃兰州 730000)
基于PLAXIS 2D堆载变化下深基坑支护结构性状研究
王 兴1,计 亲2,张克勋3
(1.安徽建筑大学土木工程学院,安徽合肥 230601;2.温州大学建筑与土木工程学院,浙江温州 325035;3.铁道部第一勘测设计院,甘肃兰州 730000)
为了深入了解深基坑开挖过程中两侧堆载变化对支护结构性状的影响规律,运用大型岩土工程有限元软件PLAXIS 2D模拟某工程基坑开挖全过程.分别计算了两侧对称堆载为0 kPa、20 kPa、40 kPa和60 kPa等不同条件下支护结构的位移、弯矩、剪力和内支撑轴力,并分析了其变化规律;然后用最小二乘法对两道混凝土内支撑轴力进行了简易拟合.计算结果表明:基坑开挖过程中堆载变化对支护结构的内力和位移有明显影响;在一定范围内支护桩最大水平位移和最大弯矩随着堆载的增加基本呈线性增加;支撑轴力的变化趋势与内支撑位置有关,不同位置的支撑随堆载的变化呈现不同的规律.
深基坑;PLAXIS 2D;变形;堆载变化
随着城市建设的快速发展,地下空间的开发利用已成为一种趋势.地下商场、地下车库、地下通道等地下建筑日益增多.在地下建筑建设过程中,经常需要基坑的开挖,支护结构是基坑工程中必要的安全措施.影响基坑变形的主要因素有:支撑或锚杆刚度、支撑或锚杆道数、预应力水平、围护结构刚度、土体变形模量等.张如林等[1-4]做了基于PLAXIS的深基坑支护数值模拟,分析了上述因素对支护结构变形和内力的影响;贺晨等[5]做了围护桩水平位移特性的分析,结果表明施加预应力是控制位移的有效方法;林刚[6]和蔡袁强等[7]分别研究了堆载不对称和挖深不同情况下基坑支护结构性状,结果表明这两种情况下支护结构都有很大的优化设计空间.
在实际工程中,施工现场条件经常是多变的,为了能够更深入了解支护结构与周边荷载的关系,本文以某工程实例为背景,在参考一些学者的研究[8-12]后分别计算了地面堆载为0 kPa、20 kPa、40 kPa和60 kPa等不同情况下支护结构的位移、弯矩、剪力和支撑轴力,通过对模拟计算结果进行分析,探讨了深基坑开挖过程中两侧堆载变化对支护结构性状的影响规律.本文研究可为某些类似的基坑工程提供一些设计参考和施工管理建议.
1 工程概况及有限元模型的建立
1.1 工程概况
某科技大楼工程,建筑面积为7 680 m2,建筑高度为32 m,基坑开挖长度36 m宽度24 m深度8 m.支护结构采用φ800 mm,间距为1 200 mm,长20 m的钻孔灌注桩.支护桩外设置φ 600@450旋喷桩止水,基坑周边有大小为20 kPa,宽度为6 m的均布荷载.设置两道混凝土内支撑,混凝土强度采用C30,支撑构件截面宽600 mm,高700 mm.内支撑分别位于桩顶和距桩顶5 m处.基坑支护结构平面布置图如图1所示,支护结构计算参数如表1所示.

图1 支护结构平面布置图
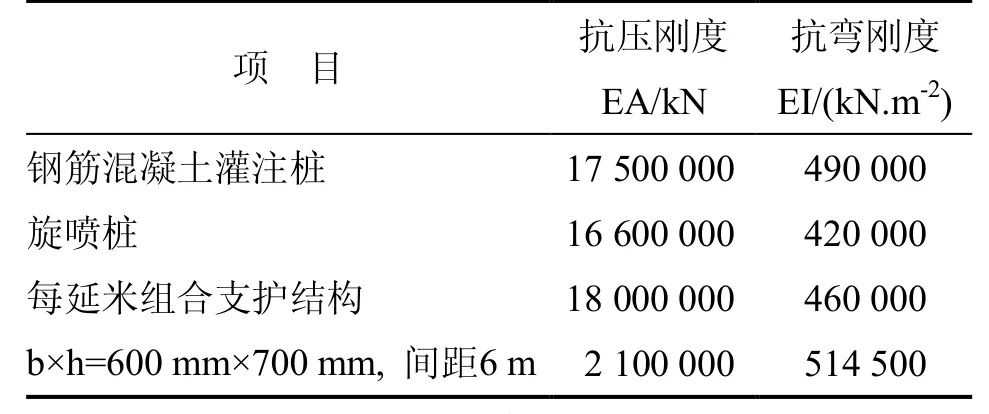
表1 支护结构计算参数表

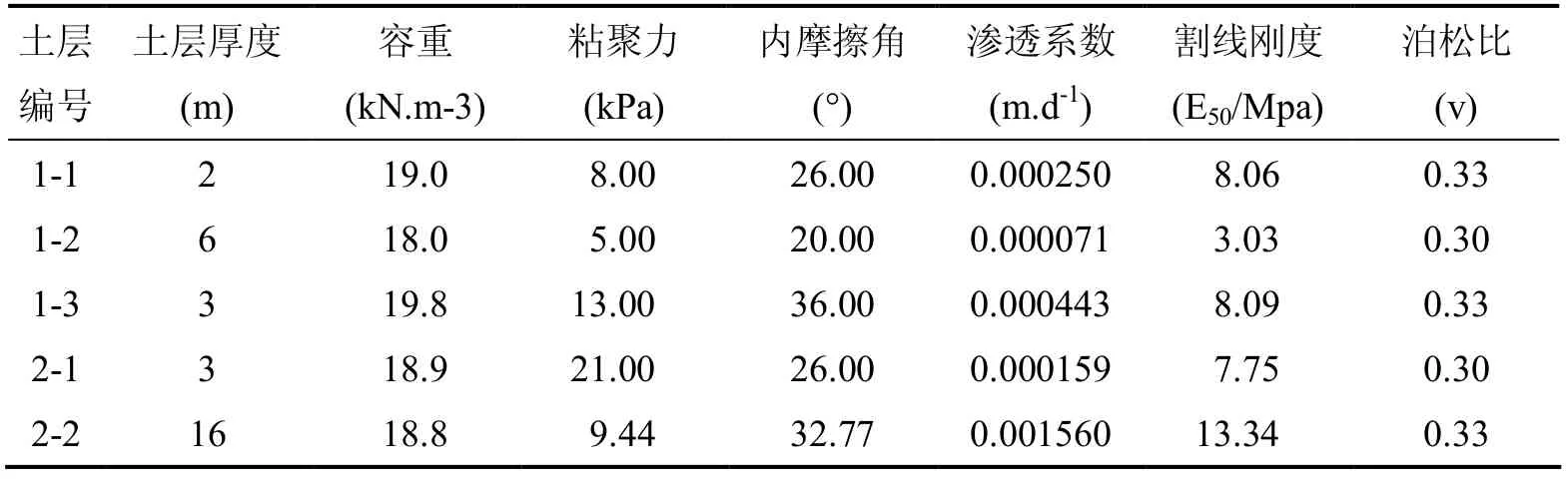
表2 土层计算参数
1.2 有限元模型的建立
PLAXIS 2D是岩土工程有限元分析软件,用于解决岩土工程的变形、稳定性及地下水渗流等问题的通用有限元系列软件.采用PLAXIS 2D进行二维平面建模,分析不同工况下支护结构的位移、内力等.
选取基坑长边中点最不利处作为二维建模分析对象.PLAXIS 2D中土体的本构模型选用考虑了卸载、再加载和初次加载时土体模量不同的Harding-Soil模型[14-15];采用15节点三角形单元模拟土体,同时建立土体与结构接触面单元,用板单元模拟挡土墙,用点对点锚杆模拟横向支撑,模型水平方向取75 m,竖向取25 m,采用标准边界条件.计算模型及有限元网格划分如图2、图3所示.
Hardening-Soil模型是一个可以模拟包括软土和硬土在内的不同类型的土体行为的先进模型,基本思想源于三轴加载下竖向应变1ε和偏应力q之间的双曲线关系.标准排水三轴试验可得到如下表示的曲线:

图2 计算模型
图3 有限元网格划分

式中:qa为抗剪强度的渐近值,qf为极限偏应力,Ei为初始刚度.

式中Eref是对应参考围压pref的参考刚度模量,在PLAXIS 2D中设置pref=100个单位应力;m为刚度应力水平相关幂指数,模拟粘土取1.0模拟砂土和粉土取0.5[16].
具体计算工况如下:
工况1:浇筑第一道混凝土内支撑,待第一道支撑达到强度要求后,开挖基坑至第二道内支撑顶面.
工况2:浇筑第二道混凝土内支撑,待第二道内支撑达到设计强度后,继续开挖至基坑设计深度.
用PLAXIS 2D分别计算堆载为0 kPa、20 kPa、40 kPa和60 kPa在以上两种工况下支护结构的位移、弯矩、剪力和内支撑轴力.

图4 不同堆载下支护桩水平位移
2 计算结果及分析
2.1 墙体水平位移分析
两种工况下左侧墙体在0 kPa、20 kPa、40 kPa和60 kPa平衡堆载作用下的水平位移如图4所示.由图4可见:
(1)当堆载为0 kPa、20 kPa、40 kPa时,两工况下墙身最大位移均发生在距桩顶7 m左右的位置;当堆载超过40 kPa时,桩体最大水平位移位置发生显著变化,其变化趋势与工况有关.在工况1下,由于基坑内侧土体开挖较少被动土压力较大,堆载的增加主要作用在支护桩的上部,所以最大水平位置相对向上移动;在工况2下,由于土体开挖至设计标高,坑内土体在坑外土体和堆载的作用下几乎发生剪切破坏,导致支护桩水平位移显著下移.
(2)但当堆载超过40 kPa时,工况1下最大水平位移位置基本不再变化,而工况2下急剧下降.当堆载为60 kPa时,最大水平位移随着两侧堆载的变化基本呈线性增加且增加的斜率相同.
(3)在桩的埋深范围内,水平位移基本都随着深度的增加而减少.
2.2 支护结构内力分析
2.2.1 墙体内力分析
在两种工况下.左侧墙体在四种不同的平衡堆载作用下的弯矩和剪力如图5所示.
由图5可见:
(1)在不同的平衡堆载作用和不同工况下,左侧墙身的最大弯矩位置没有发生明显的变化,一直都在-5.0 m左右.当堆载增加至60 kPa时,第二道支撑处的弯矩没有减小反而成为弯矩的最大控制截面,并且埋深内出现了负弯矩.
(2)由剪力图可见当堆载超出40 kPa后,第二道支撑处剪力值不再发生突变,而是坑底临近发生突变,这是因为堆载过大时支护结构发生较大几何变形和应力在途中的传递路径共同作用的结果.
不同堆载下的最大位移和最大弯矩随堆载增加的变化图如图6所示.
依据等值梁法,在多支点基坑支护结构中,支点间的支护桩可看作竖直简支连续梁来分析.简支梁的挠度公式为:

其中EI为支护桩的水平抗弯刚度是常数,S为调整系数也为常数,l0为计算跨度.
由图6可见,堆载在一定范围内时弯矩和最大水平位移是线性变化的,然而两者斜率变化并不相同.工况1下,弯矩变化斜率大于工况2下的斜率;而两工况下的最大水平位移变化斜率却相同.由公式(4)可知,在简支条件下,最大水平位移与最大水平弯矩呈正比关系.因此,最大水平位移也与最大弯矩和EI的比值成正比.由图6可见,最大弯矩斜率相差为Δk =1.155-0.850=0.305,由于EI足够大所以Δk/ EI趋于零,所以最大水平位移的斜率趋于相同,软件数值模拟结果与理论分析结果相吻合.

图6 弯矩和最大水平位移随堆载变化曲线图
2.2.2 支撑结构轴力拟合分析
基坑开挖完成后,两道内支撑轴力分别如表3所示;采用最小二乘法拟合堆载与支撑轴力的相关关系,拟合结果如图7所示.

表3 支撑在不同堆载下的轴力(kPa)
由图7可见:
(1)本基坑实例中随着堆载的变化,第一道支撑轴力与堆载呈三次立方关系;第二道支撑轴力与堆载呈线性关系.
(2)两条曲线的拟合均比较理想,相关系数都十分接近于1,拟合公式(5)和(6):
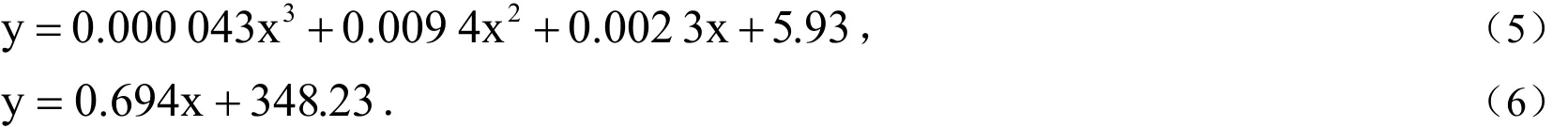
(3)地面堆载的变化对两道支撑轴力影响都较为明显;第一道支撑内力对于堆载的变化要更为敏感.
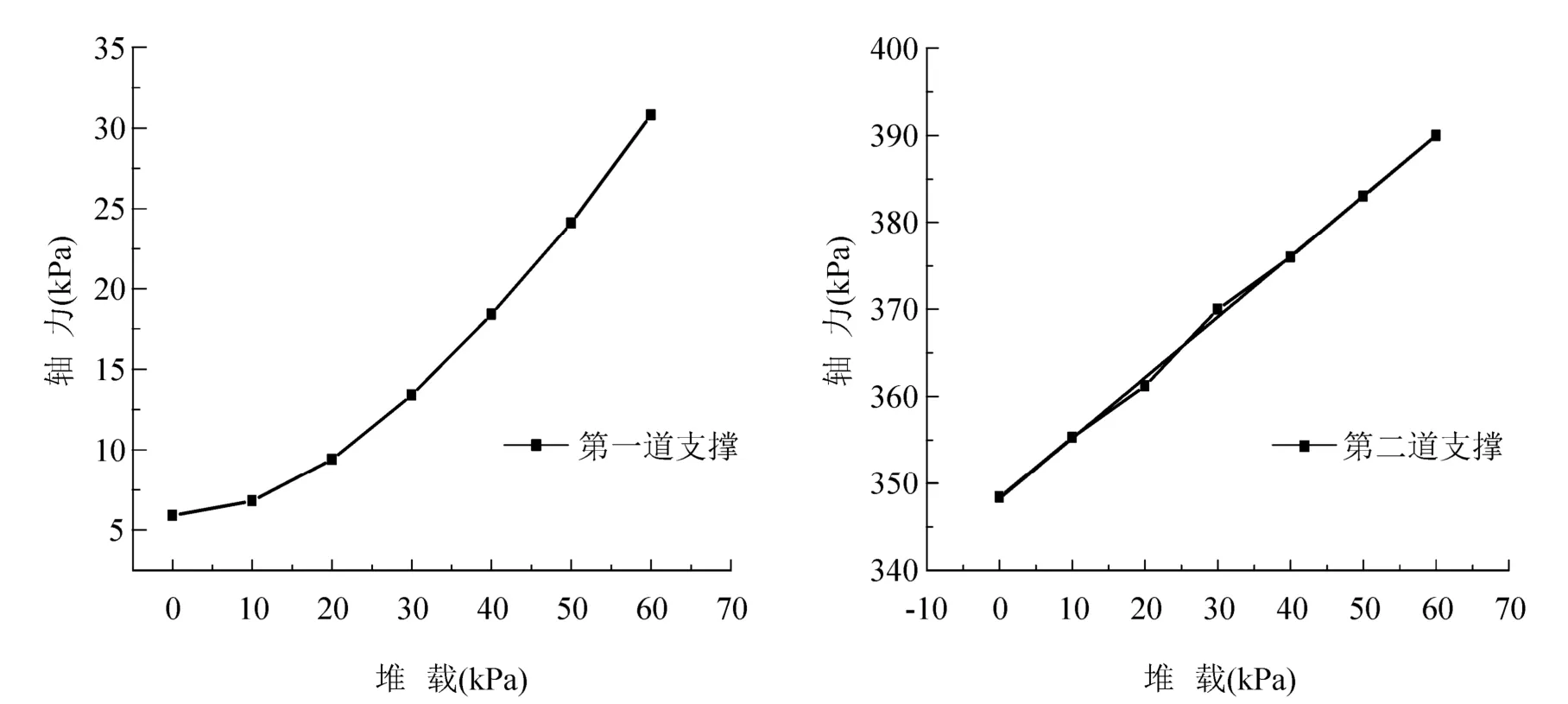
图7 两道支撑轴力与堆载关系曲线图
(4)为验证拟合曲线的准确性,对比了堆载为80 kPa下的实际支撑内力和拟合内力,如表4所示.

表4 实际内力与拟合结果对比
3 结 论
通过上述计算和分析得出以下结论:
(1)通过对基坑工程的模拟得到了详细的支护结构变形和内力数据,更加清晰的了解了支护结构的内力变化,以及更准确的确定了结构的薄弱位置.
(2)在一定的堆载变化范围内,堆载的变化主要影响开挖面以上的部分,支护结构性状变化趋势相同.在超出一定的范围后,由于支护桩受力过大将导致基坑底部土体局部剪切破坏,支护桩最大水平位移位置下移.
(3)本例中堆载的变化对处于工况2下的弯矩影响比较明显,与水平位移有着同样的变化趋势;对处于工况1下的内力影响相对较小,这是因为工况2下开挖深度较大,内侧对支护桩有利的被动土压力丧失,基坑底部土质较差致使基坑底部桩体位移较大.
(4)堆载的变化对两道支撑的应力影响都比较明显.两道支撑的应力都随着堆载的增加不断增大,但增加的规律与支护的位置和应力的传递方式有关.
[1] 张如林, 徐奴文. 基于PLAXIS的深基坑支护设计的数值模拟[J]. 结构工程师, 2010, 26(2): 131-136.
[2] 许云云, 孙仲强. 基于PLAXIS 2D的基坑支护中内支撑对支护桩的影响分析[J]. 唐山学院学报, 2010, 23(3): 22-24.
[3] 顾凤祥, 阎怀瑞, 阎长虹, 等. 深基坑支护结构数值模拟[J]. 中国水运, 2011, 11(8): 159-161.
[4] 冯永红. 软土地基超深基坑土方开挖的监测与有限元分析[D]. 杭州: 浙江大学建筑工程学院, 2012: 76-81.
[5] 贺晨. 基于PLAXIS基坑围护桩水平位移特性的分析[J]. 中南林业科技大学学报, 2011, 31(8): 142-146.
[6] 林刚, 徐长节, 蔡元强. 不平衡堆载作用下深基坑开挖支护结构性状研究[J]. 岩土力学, 2010, 31(8): 2592-2598.
[7] 蔡袁强, 李碧青, 徐长节. 挖深不同情况下基坑支护结构性状研究[J]. 岩土工程学报, 2010, 32(增刊1): 28-31.
[8] 刘晓丽, 马悦, 郭冠群. PLAXIS 2D模拟计算基坑开挖工程的适用性分析[J]. 中国海洋大学学报, 2012, 42(4): 19-25.
[9] 李青. 软土深基坑变形性状的现场试验研究[D]. 上海: 同济大学土木工程学院, 2008: 43-48.
[10] 陈敏华, 陈增新, 张长生. FLAC在基坑开挖分析中的应用[J]. 岩土工程学报, 2006, 28(增刊): 1437-1440.
[11] 王艳峰. 软土地区基坑工程变形性能分析[D]. 上海: 同济大学土木工程学院, 2008: 40-46.
[12] 陈忠汉, 黄书秩, 程丽平. 深基坑工程[M]. 北京: 机械工业出版社, 2003: 60-133.
[13] 谢康和, 周建. 岩土工程有限元分析理论与应用[M]. 北京: 科学出版社, 2002: 293-301.
[14] Hardin B O, Drnevich V P. Shear modulus and damping in soils: Design equations and curves [J].Journal the soil Mechanics and Foundations Division, 1972, 98(7): 667-692.
[15] Hardin B O, Black W L. Closure to vibration modulus of normally consolidate clays [J]. Journal the soil Mechanicsand Foundations Division, 1969, 95(6): 1531-1537.
[16] Janbu J. Soil compressibility as determined by oedometer and triaxial tests [J]. ECSMFE Wiesbaden, 1963, 1: 19-25.
Study on Supporting Structure Characters of Deep Foundation Excavation under Various Heaped Load Based on PLAXIS 2D
WANG Xing1,JI Qin2,ZHANG Kexun3
(1. School of Civil Engineering, Anhui Jianzhu University, Hefei, China 230601; 2. College of Architecture and Civil Engineering, Wenzhou University, Wenzhou, China 325035; 3. The First Survey and Design Institute, Ministry of Railways, Lanzhou, China 730000)
This paper utilizes PLAXIS 2D to simulate the overall process of a foundation excavation in order to reveal the influence rule of both heaped loads to the supporting structures. Through calculating respectively bilateral symmetry heaped load as well as the brief analysis on its varying rules: from 0 kPa to 60 kPa and 40 kPa to 60 kPa, the displacement, bending moment, shearing force and internal bracing force under different conditions are obtained with simple matching to the axial force of the two internal supporting structures by least square method. The analytical results show that there is obvious influence on the supporting structures when the heaped load is changed. The maximum moment and the maximum horizontal displacement increase with the heaped load becoming larger within limits. While, the variation trend of supporting axial force is related to its internal bracing position, that is, supporting structure at different position takes on different rules.
Deep Foundation Excavation; PLAXIS 2D; Deformation; Heaped Load Variation
TU476
A
1674-3563(2014)04-0048-07
10.3875/j.issn.1674-3563.2014.04.008 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:封毅)
2013-11-11
王兴(1989- ),男,河北定州人,硕士研究生,研究方向:地下结构计算理论与应用

