改进的节块展开法求解对流扩散方程的稳定性和误差分析
邓志红1,孙玉良1,李 富1,Rizwan-uddin2
(1.清华大学 核能与新能源技术研究院,北京 100084;2.伊利诺伊大学 香槟分校,伊利诺伊州 61801,美国)
改进的节块展开法求解对流扩散方程的稳定性和误差分析
邓志红1,孙玉良1,李 富1,Rizwan-uddin2
(1.清华大学 核能与新能源技术研究院,北京 100084;2.伊利诺伊大学 香槟分校,伊利诺伊州 61801,美国)
对改进的节块展开法(MNEM)求解对流扩散方程进行了深入研究。利用符号不变原则理论上分析了MNEM的稳定性,分析结果显示,MNEM是一种具有固有稳定性的求解方法。通过数值实验对MNEM的计算误差进行了分析。数值结果表明:对于一维问题,MNEM至少具有3阶精度;对于多维问题,受横向泄漏近似的影响,MNEM表现为2阶精度。
改进的节块展开法;对流扩散方程;稳定性;误差分析
现代节块法,因其在精度和效率方面的优势,已广泛应用于反应堆物理计算中。但在反应堆安全分析程序中,热工问题的计算依然普遍采用有限差分或有限体积方法求解。为改进物理-热工计算效率,在节块法的构架下统一求解物理-热工耦合问题是朴素而直接的想法。应用节块法求解反应堆热工问题的研究相对较少,其中,节块积分法(NIM)在求解对流扩散方程和Navier-Stokes方程方面已取得不错进展[12]。但其对虚拟源项通常采用0阶近似,无法实现物理-热工的高阶耦合,损失了计算精度。研究表明,传统的节块展开法求解对流扩散方程只具有条件稳定性(网格临界Peclet数小于4.644),其稳定性虽优于中心差分方法,但在对流占优的情况下采用粗网节块将会带来非物理的数值振荡,精度很差[3]。为了保持节块展开法对高阶源项的处理能力,且改善节块展开法的求解稳定性,本文提出改进的节块展开法(MNEM)来求解对流扩散方程,并基于离散格式稳定性分析方法(符号不变原则)对MNEM的稳定性进行理论分析,根据数值实验对其求解对流扩散方程的误差进行分析。
1 基本方程
稳态三维对流扩散方程为:
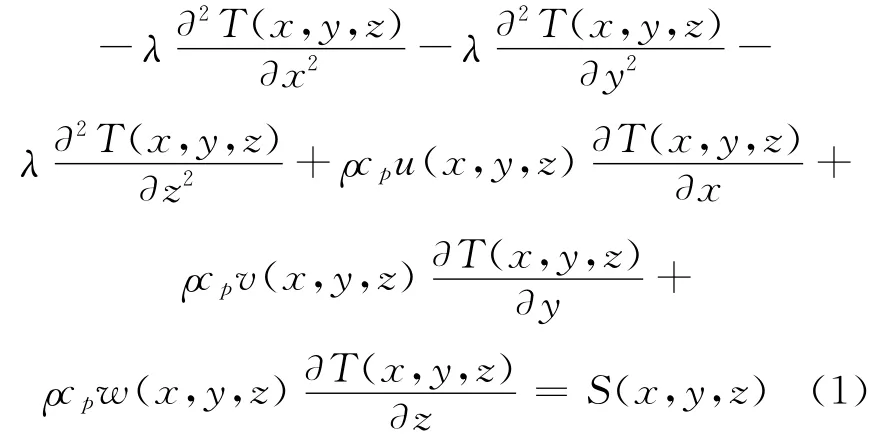
式中:T为温度;ρ为密度;cp为比定压热容;λ为导热系数;u、v、w分别为3个方向的速度;S为源项。
与求解中子扩散方程类似,节块展开法求解对流扩散方程的一般过程为:首先采用横向积分技术将多维的偏微分方程转化为多个一维的常微分方程;对节块内的偏温度采用基函数进行展开,利用Galerkin剩余权重法得到3个矩权重方程;利用节块界面处的连续条件(偏温度连续和偏温度梯度连续)最终得到截面偏温度的离散方程;利用平衡方程求解节块的平均温度。
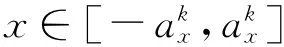
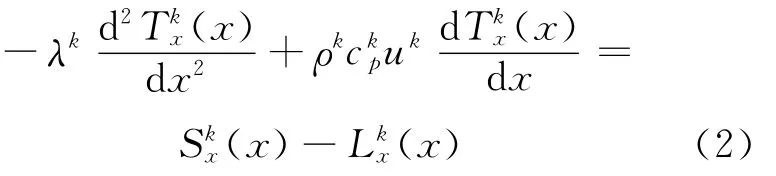
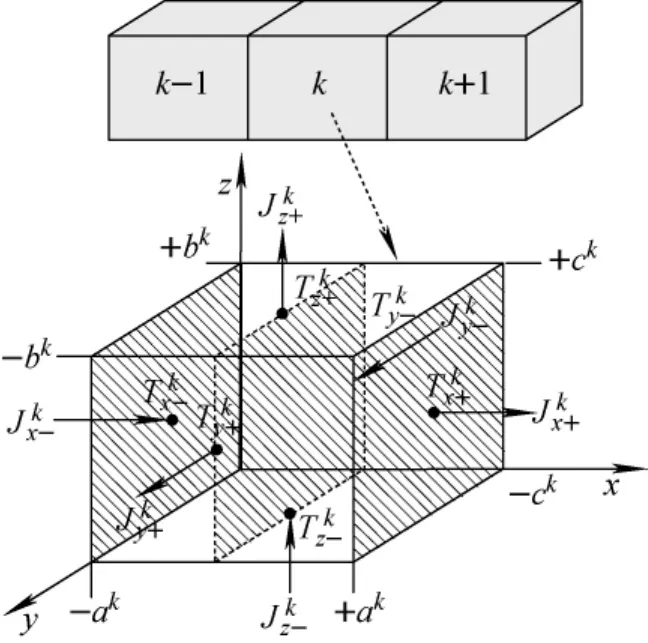
图1 节块划分示意图Fig.1 Domain discretization for nodal expansion method
对流扩散方程与中子扩散方程不同,由于对流项的存在,其解可能发生剧烈变化,尤其当对流占优时。由于对流扩散方程的解剧烈振荡,传统差分方法在求解该方程时会遇到稳定性问题,通常需选取非常细的网格来避免数值振荡,因此极大限制了其计算效率。为改善传统节块展开法(NEM)求解对流扩散方程的稳定性,本文中提出的MNEM采用了速度的指数函数代替原来第4阶多项式作为展开函数,数值结果表明其极大地提高了传统NEM的稳定性。
节块的x方向的偏温度展开如下:
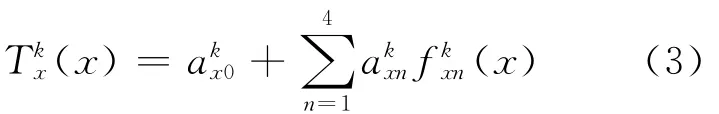
在MNEM中,代替原来第4阶展开多项式的指数函数为:
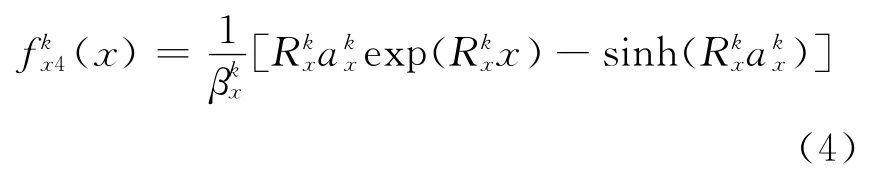
该指数函数满足:
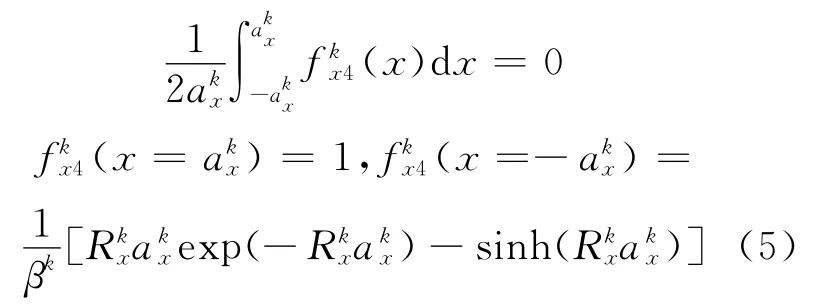
节块边界处的偏温度和偏温度梯度为:
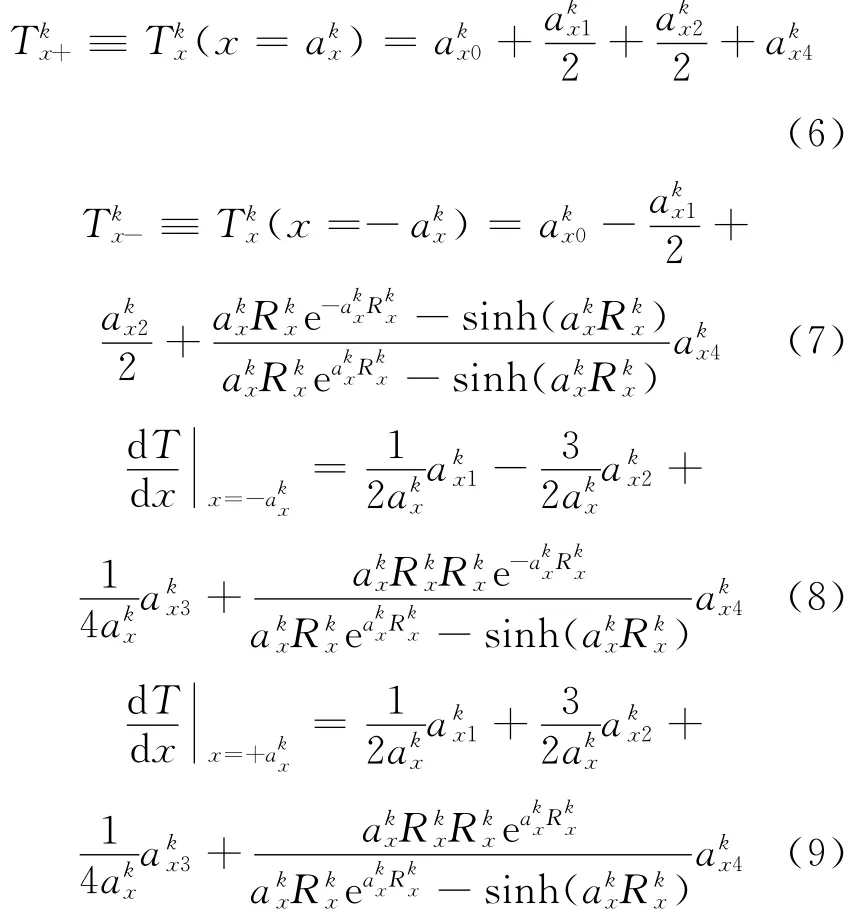
在MNEM中,与传统NEM类似,源项仍采用2阶多项式展开。但其泄漏项的处理与中子扩散方程不同,由于对流扩散方程的解变化剧烈,传统NEM中关于横向泄漏的假设(3个相邻节块的横向泄漏形状相同,且为2阶多项式)已不再成立。数值实验表明,求解对流扩散方程时若仍采用原来的横向泄漏近似方法,会由于简单近似带来的数值振荡(尤其当对流占优时)影响方法的整体计算精度。因此,本文仅对横向泄漏进行0阶近似,即:
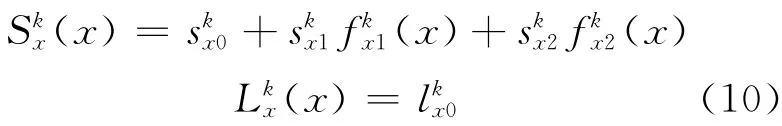
在MNEM中,Galerkin剩余权重法被用来产生3个矩权重方程,其过程为:
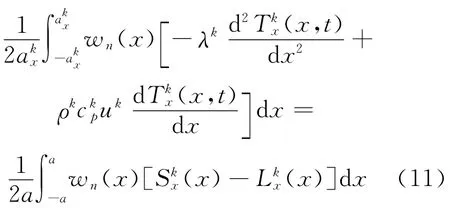
其中,wn(x)为权重函数。
选取w0(x)=1、w1(x)=fx1(x)、w2(x)=fx2(x),将得到3个矩权重方程,分别为:
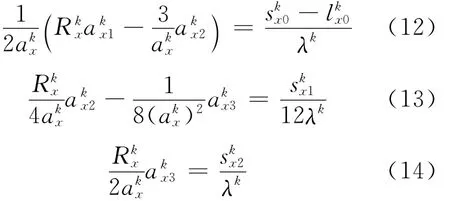
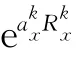
2 MNEM稳定性分析
为了说明MNEM较传统NEM求解对流扩散方程的优势,本文将从理论上分析MNEM的稳定性。稳定性分析通常基于简单的一维问题[4],且在NEM中,多维的偏微分方程将通过横向积分技术变为多个一维的常微分方程,因此,基于一维问题的分析向多维问题拓展是直接的。
考虑一维稳态线性对流扩散方程为:
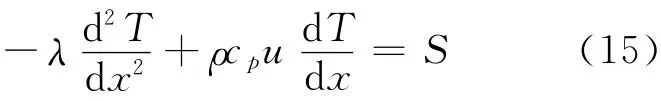
为便于稳定性分析,假设上述参数在计算区域内恒定,且计算区域被划分为相同尺寸节块,节块半宽度为a。由于流速为0时,对流扩散方程蜕化为扩散方程,通常无需考虑稳定性问题。因此,推导过程中假设流速不为0。
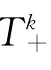
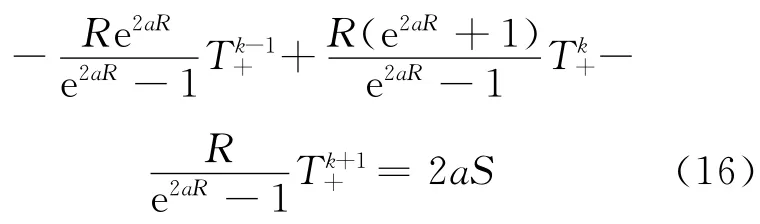
其中,R=ρcpu/λ。
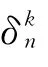
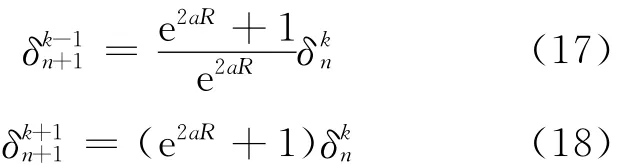
根据符号不变原则,稳定性保持的条件为:

由式(17)、(18)可知,无论速度的大小和方向,MNEM的离散形式始终满足稳定性条件(式(19)),即网格Peclet数可为任意值。本文给出的稳定性分析虽是基于简单的一维、常系数、定温边界条件下得到的,但研究表明,此时得到的网格临界Peclet数是较为苛刻条件下的值,对于原假设条件的偏离均会使得网格临界Peclet数有所增加[5]。因此,最终可得到稳定性分析的结论:MNEM是一种具有固有稳定性的方法。
3 数值结果与分析
基于文中的推导过程,开发了求解对流扩散方程的程序。
3.1 一维问题
1)一维无源

其中,C=ρcpu/λ。为了考察MNEM的稳定性和计算精度,图2示出了C=-100、-10、0.5、10、100时MNEM的计算结果。节块的尺寸划分均匀,均为0.2。为了更好地描述MNEM的计算精度,图2也示出了MNEM在节块中的详细温度分布。
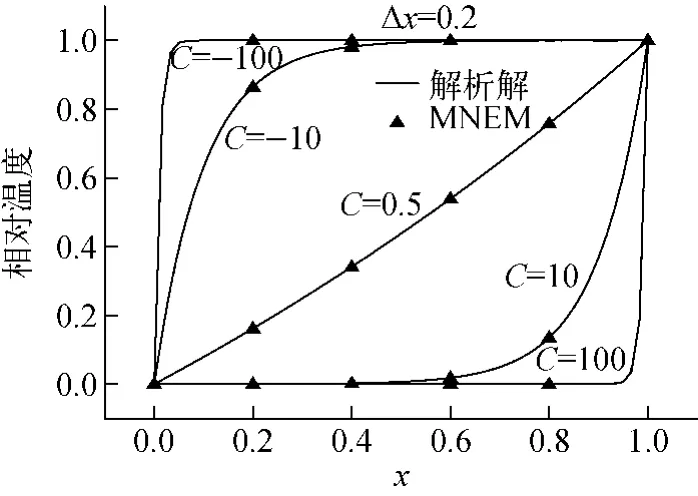
图2 不同C值时MNEM的计算结果与解析解的对比Fig.2 Comparison between MNEM and analytical solution for different C
由图2可知,对于不同的C值,MNEM的计算结果均与解析解符合得非常好,即使当C=±100、温度梯度很大时,MNEM依然能很好地跟踪温度的变化。且无论流速的大小和方向,MNEM的计算结果均保持数值稳定性,表明MNEM具有固有的迎风特性。
2)一维有源
为进一步验证MNEM求解带源问题,本文将计算带分布源的一维对流扩散问题:
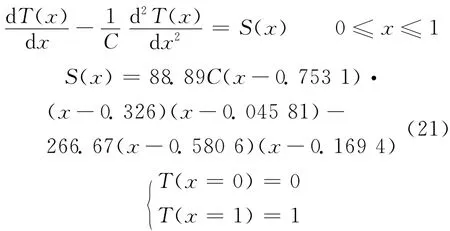
图3示出C=1 000时,不同节块数目下MNEM的数值解同解析解的比较。
由图3可知,节块数N=2、5、10时均能得到很好的结果,即计算得到的节块平均值同解析解平均值符合得非常好。且计算区域中温度的变化剧烈,即便如此,MNEM采用非常少的节块(如N=2)依然能得到稳定、高精度的结果,表征了MNEM计算对流扩散问题的能力。
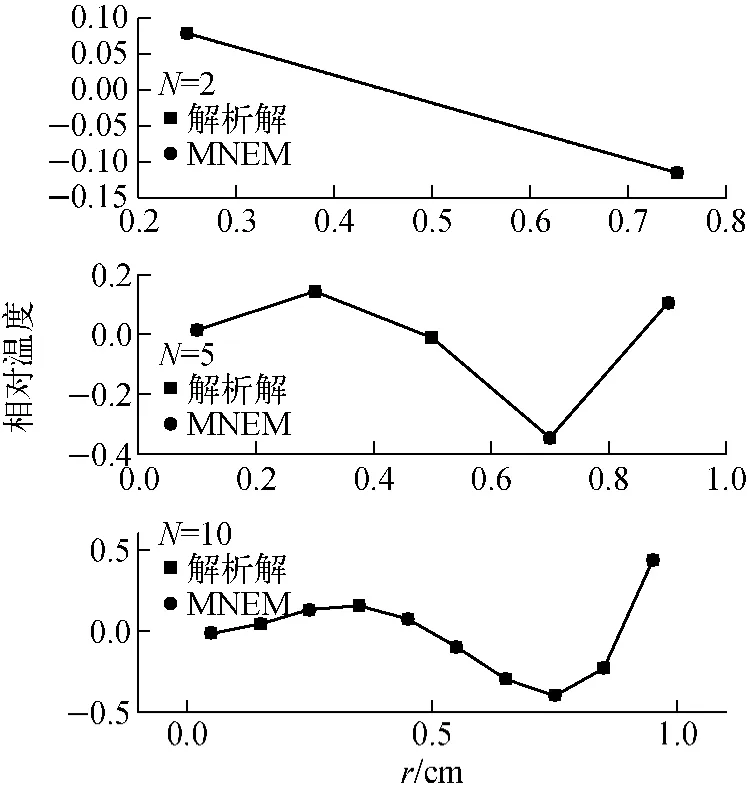
图3 MNEM数值解与解析解的对比Fig.3 Comparison between MNEM and analytical solution
为进一步分析MNEM的特点,表1列出C取不同值时MNEM和NIM计算本算例的均方根(RMS)误差随节块尺寸的变化情况。RMS误差定义如下:
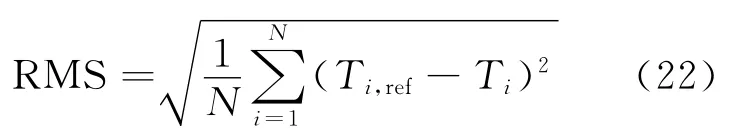
其中,Ti为数值解,Ti,ref为与之对应的参考解。
由表1可知,在各种C和节块划分的情况下,MNEM的RMS误差均比NIM的小,精度优势非常明显。为比较二者的精度阶次,图4示出RMS误差随节块尺寸变化的对数关系。由图4可见,MNEM的误差在对数图中的斜率最小为3.10,表征计算该一维带源问题,MNEM的最低收敛精度为3阶。NIM的误差斜率则全部为2.0,符合文献[1]中采用0阶源项展开时NIM是2阶精度的论断。
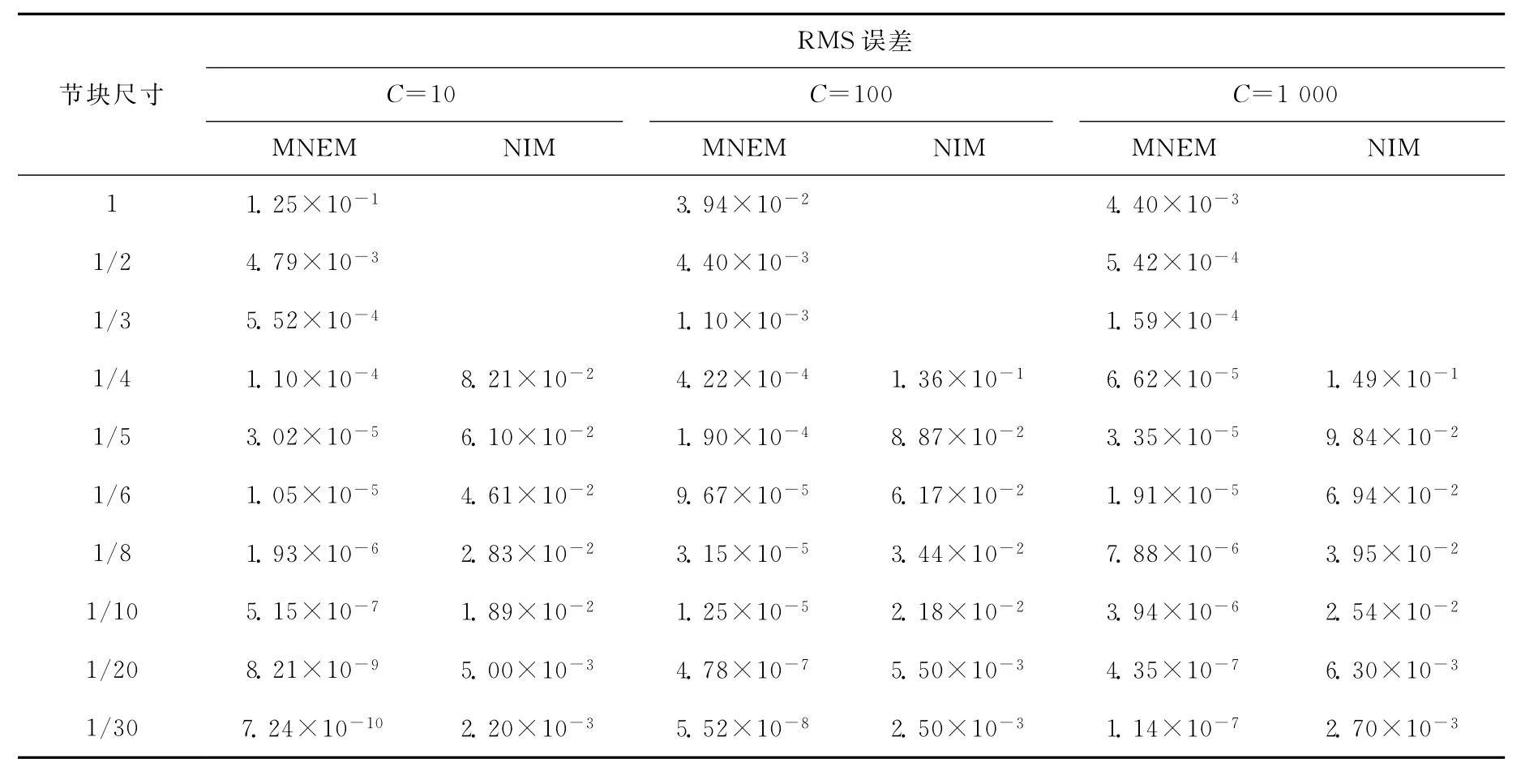
表1 MNEM和NIM的RMS误差随节块尺寸的变化Table 1 RMS errors of MNEM and NIM versus node-size
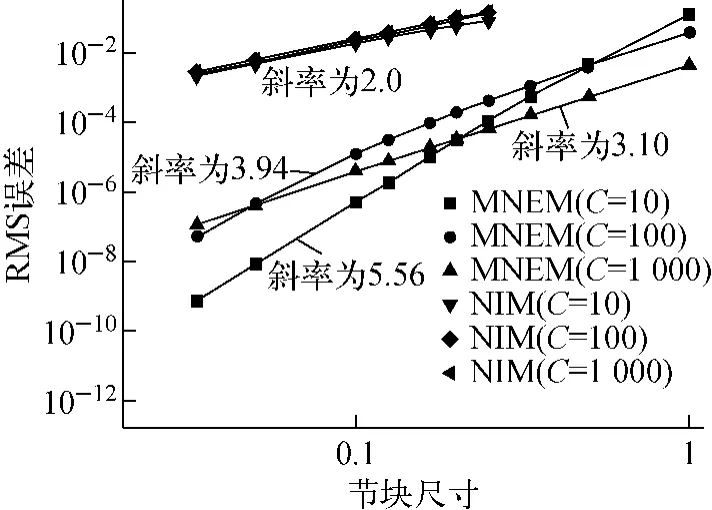
图4 MNEM和NIM求解一维问题的RMS误差随节块尺寸的变化Fig.4 RMS errors of MNEM and NIM versus node-size for 1Dproblem
3.2 二维无源问题
二维无源问题的计算公式为:
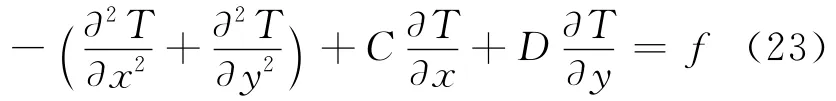
其中:
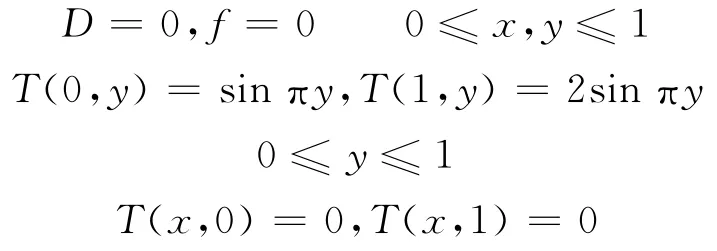

其解析解[5]为:
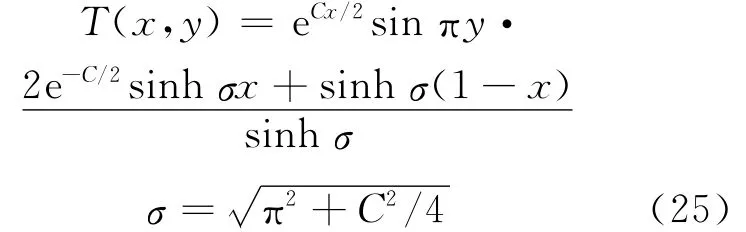
为说明MNEM的计算精度,选定计算区域中y方向的中线位置(y=0.5)处的区域。图5示出C分别为100和1 000时,不同节块尺寸下MNEM和NIM的数值解与解析解的结果比较。由图5可见,MNEM的数值解同解析解均符合得非常好,且同NIM的结果一致。需要说明的是,由于图5给出的均是节块平均温度,因此不同节块划分情况下的温度曲线存在一定的差异。
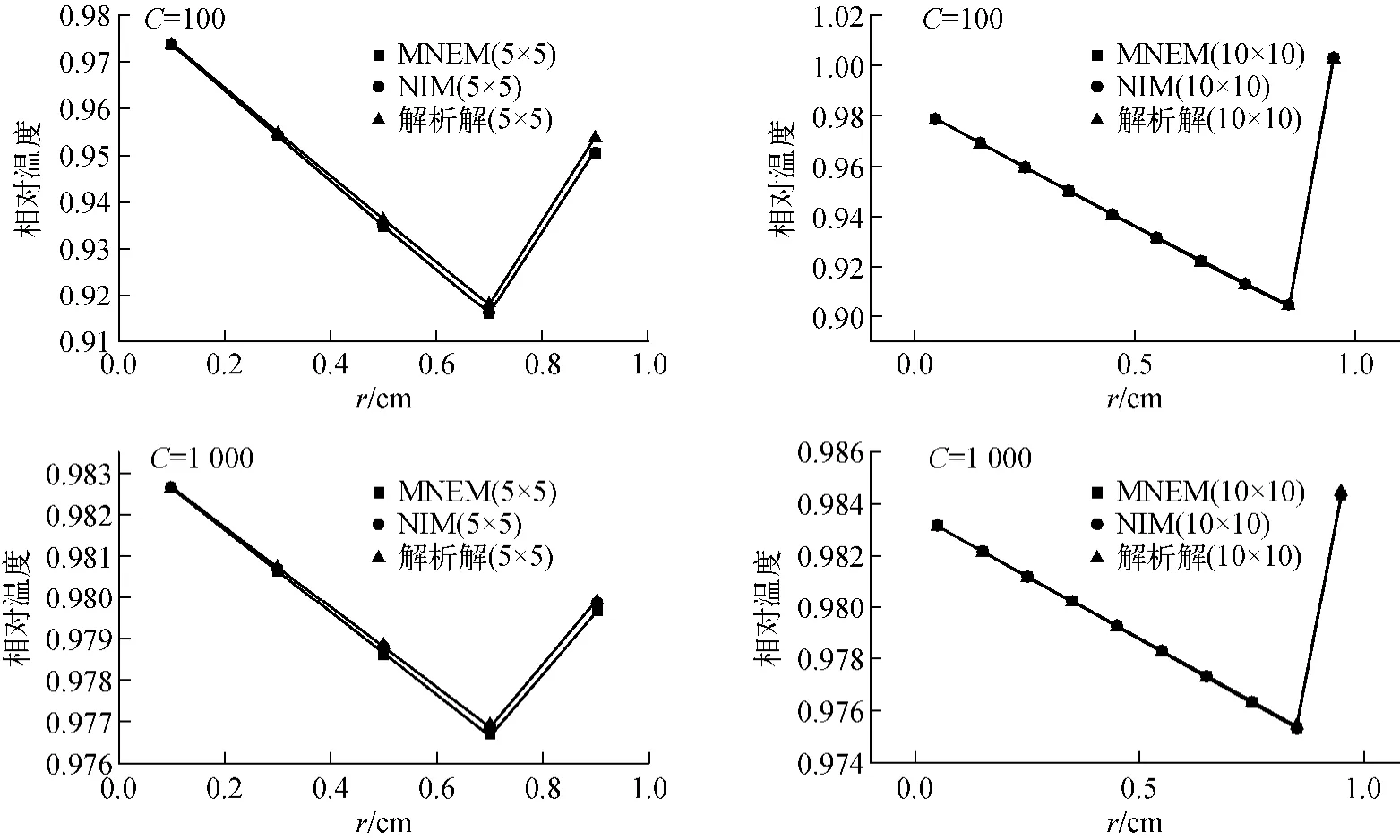
图5 MNEM和NIM的数值解同解析解的对比Fig.5 Numerical solution of MNEM and NIM versus analytical solution
为说明MNEM计算多维对流问题的计算精度,表2列出C分别为100和1 000、不同节块划分时MNEM与NIM的RMS误差。由表2可见,在各种节块划分情况下,MNEM和NIM的误差基本相当,但NIM的误差稍微优于MNEM的。

表2 二维无源问题MNEM和NIM的RMS误差随节块尺寸的变化Table 2 RMS errors of MNEM and NIM versus node-size for 2Dproblem without source
图6示出C为100和1 000时,MNEM和NIM的RMS误差随节块尺寸的变化。由图6可见,二者无论是误差值还是误差的变化率均基本一致,表明对于二维无源问题,二者的计算精度相当,且均为2阶。本算例的结果与一维有源问题的结果存在差异的原因是:本算例中源项为零,因而横向泄漏近似是本问题中唯一的近似。由于MNEM和NIM均采用横向泄漏项的0阶近似,因此二者的计算结果与精度相当。
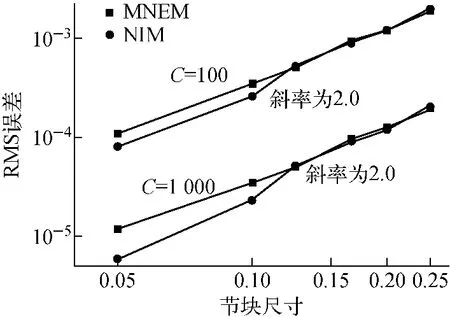
图6 MNEM和NIM求解二维问题的RMS误差随节块尺寸的变化Fig.6 RMS errors of MNEM and NIM versus node-size for 2Dproblem
4 结论
本文深入研究了MNEM求解稳态对流扩散方程的特性。基于一维线性无源对流扩散方程,利用符号不变原则从理论上分析了MNEM的稳定性,分析表明,该方法具有固有的稳定性,对网格Peclet数无限制。基于一系列数值实验研究了MNEM求解对流扩散方程的精度,计算结果表明:对于一维问题,MNEM至少具有3阶精度;对于多维问题,由于MNEM目前仍采用简单的横向泄漏近似,其精度表现为2阶。后续工作将进一步研究有效的横向泄漏近似方法,使MNEM计算对流扩散问题的精度整体提高到3阶,同时将研究节块法求解流动方程的可行性,从而最终实现在节块法的框架下求解物理-热工问题。
[1] Rizwan-uddin.A second-order space and time nodal method for the one-dimensional convectiondiffusion equation[J].Computers &Fluids,1997,26(3):233-247.
[2] TOREJA A J.A nodal approach to arbitrary geometries,and adaptive mesh refinement for the nodal method[D].USA:University of Illinois,Urbana,IL,2002.
[3] DENG Z H,Rizwan-uddin,LI F,et al.Stability and error analysis of nodal expansion method for convection-diffusion equation[C]∥Proceedings of ICAPP2012.Chicago:[s.n.],2012.
[4] TAO W Q,SPARROW E M.The transportive property and convective numerical stability of the steady-state convection-diffusion finite-difference equation[J].Numerical Heat Transfer,1987,11(4):491-497.
[5] GUPTA M M,MANOHAR R P,STEPHENSON J W.A single cell high order scheme for the convection-diffusion equation with variable coefficients[J].International Journal for Numerical Methods in Fluids,1984,7(4):641-651.
Stability and Error Analysis on Modified Nodal Expansion Method for Transient Convection-diffusion Equation
DENG Zhi-hong1,SUN Yu-liang1,LI Fu1,Rizwan-uddin2
(1.Institute of Nuclear and New Energy Technology,Tsinghua University,Beijing100084,China;2.Nuclear,Plasma,Radiological Engineering,University of Illinois at Urbana-Champaign,Urbana 61801,USA)
To further investigate the features of modified nodal expansion method(MNEM)for solving the convection-diffusion equation,the stability and error analysis were carried out.Based on sign preservation principle,the stability analysis reveals that the MNEM has inherent stability.The error analysis was implemented through a series of numerical experiments,and the results show that the MNEM is 3rd order scheme for one dimensional problem,while as 2nd order scheme for multi-dimensional problem because of using simple transverse leakage approximation.
modified nodal expansion method;convection-diffusion equation;stability;error analysis
O24
A
1000-6931(2014)02-0298-07
10.7538/yzk.2014.48.02.0298
2012-10-16;
2013-01-15
国家重大科技专项经费资助项目(ZX06901)
邓志红(1984—),男,湖南衡阳人,博士研究生,核科学与技术专业

