从一道题的解法谈古典概型基本事件总数的确定

王宏平

（江苏省司法警官高等职业学校公共基础教研室，江苏镇江 212003）

从一道题的解法谈古典概型基本事件总数的确定

王宏平

（江苏省司法警官高等职业学校公共基础教研室，江苏镇江 212003）

古典概型是高职数学教学中的难点之一，确定基本事件总数是解决这类问题的关键。基本事件总数确定的方法有很多种，在解决问题时要灵活运用。

古典概型；基本事件；总数确定

古典概率问题对大多数高职学生来说是一件既感到好奇又感到头疼的事，古典概率往往能激起他们的学习兴趣，但解决问题时往往不知该如何下手，做出的答案也不知对错。

由事件A发生的概率可知，求事件A发生的概率，通常分成两步：

1）选取适当的样本空间，使其满足有限、等可能的要求。

2）确定样本空间中基本事件总数和基本事件数［1］。

大多数人认为基本事件总数容易确定，一般不会出错，其实不然。江苏省职业学校新编教材《数学》第二册中有一道题为：

有红、黄、蓝3种颜色的小旗各3面，任取其中3面，求：

1）3面小旗全是红色的概率；

2）恰有2面小旗是红色的概率。

编者给出了问题1）的参考答案，即单色旗有3种（红红红、黄黄黄、蓝蓝蓝），双色旗有6种（红红黄、红红蓝、黄黄红、黄黄蓝、蓝蓝红、蓝蓝黄），三色旗有1种（红黄蓝），故基本事件总数是

3+6+1=10，

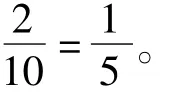
这个解答中，对基本事件总数的确定存在问题。

1 古典概型概率的概念

具有下列两个特点的随机试验所对应的概率模型称为古典概型：

1）随机试验的样本空间只包含有限个基本事件；

2）随机试验中每个基本事件发生的可能性相同［2］。

如果一次试验的等可能事件共有n个，那么每一个等可能基本事件发生的概率都是。如果某个事件A包含了其中m个等可能基本事件，那么事件A发生的概率

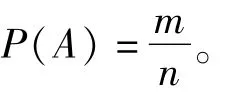
使用古典概型求概率，必须先确定问题是否属于古典概型，若属于，则进一步确定基本事件的总数及所求事件包含的基本事件数。

2 错误原因分析

很显然，根据古典概型的概念，上文中的“选旗问题”应属于古典概型。因为每面小旗被取到的可能性相同，所以是一个等可能随机试验，且出现的基本事件只有有限个。若以被取的小旗的颜色分类，所有可能出现的基本事件可以分为10类，即红红红、黄黄黄、蓝蓝蓝、红红黄、红红蓝、黄黄红、黄黄蓝、蓝蓝红、蓝蓝黄、红黄蓝。原教材编者把基本事件发生的10个种类数当成了基本事件的总数，二者不能划等号。

如果把3面红色小旗、3面黄色小旗、3面蓝色小旗分别标上序号，记为红1，红2，红3；黄1，黄2，黄3；蓝1，蓝2，蓝3。以出现双色旗“红红黄”这一事件为例，基本事件数应是9，即红1红2黄1，红1红2黄2，红1红2黄3，红1红3黄1，红1红3黄2，红1红3黄3，红2红3黄1，红2红3黄2，红2红3黄3。

类似地，出现其他5种类型双色旗的基本事件数也是9，这样，出现双色旗的基本事件数应该是

6×9=54。

同理，出现三色旗的基本事件数为27。

出现单色旗的基本事件有：红1红2红3，黄1黄2黄3，蓝1蓝2蓝3，即出现单色旗的基本事件数是3。

因此，基本事件总数是

54+27+3=84。

这84个基本事件中的每一事件都是等可能随机事件，而出现3面全是红色小旗的基本事件数是1，从而出现3面全是红色小旗的概率应该是

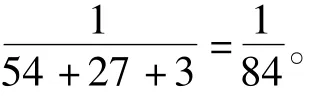
类似地，恰有两面是红色小旗的基本事件数不是2，而是18，所以恰有两面是红色小旗的概率是

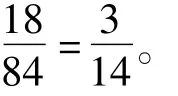
每次选出的3面小旗，只有这10类基本事件中的某一类会发生，但每一类基本事件并不是等可能发生的，不属于古典概型问题，不能用古典概型的概率公式解决。

例1有红球1个，白球1个，其大小形状都相同，现从中任意取出一个小球，问取到红球的概率是多少？

分析任意取出一个球，从颜色上分，只有红或白两种结果，其基本事件种类数是2，如果以此认为基本事件总数也是2，即这个问题的答案是，那么改变条件，如红球10个，白球1个，基本事件种类数依旧是2，得到的结果仍然还是，显然不通。

因此，确定古典概型中基本事件总数时，一定要从基本概念出发，不能将基本事件种类数当成基本事件总数来计算概率。

3 古典概型基本事件总数的确定

3.1 合理运用排列组合的基本原理

在古典概型中，所进行的试验都是等可能随机试验，且出现的基本事件数是有限的，其基本事件总数的确定有时可以借助于排列组合的基本原理来进行。比如，上文中的“选旗问题”，其基本事件总数可以运用组合公式确定，即=84。

例2有n个人，每个人以同样的概率分配到N（n＜N）个房间中的一间，求某指定n间房中各有1人的概率是多少？

分析这个问题既不是从N间房中任选n间房，也不是从N间房中任选n间房按照一定顺序排列，所以其基本事件总数不能用组合数或排列数来确定，而应该用分步计数原理（乘法原理）确定。由题意知，每个人都以同样的概率被分配到某间房，即第1人有N种可能，第2人有N种可能…第n人有N种可能，共有

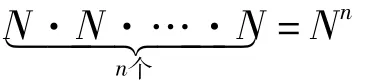
种可能，从而基本事件总数应该是Nn。

3.2 基本事件数与基本事件总数属于同一样本空间

在同一个古典概型问题中，只要保持基本事件的等可能性，样本空间可以有不同的取法，但在计算时，基本事件数和基本事件总数一定要在同一个样本空间中，否则就会产生错解［3］。

例3有10件产品，其中7件是正品，3件是次品，现每次从中取出1件产品，取后不放回，连取3次，求取到的产品中恰有1件是次品的概率。

分析设事件A=｛所取的3件产品中恰有1件次品｝。

由于3件产品是一件一件取出的，取法与先后顺序有关，所以样本空间中共有P个基本事件。另一方面，题中只关心所取的3件产品中有1件是次品，并不关心这1件次品是在哪一次取出的，因此，可以用组合数构成另一个样本空间。如果将事件的概率解为

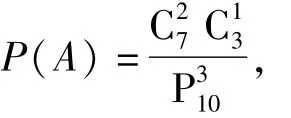
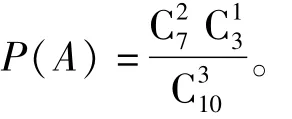
3.3 巧取样本空间

选取恰当的样本空间是解决古典概型问题的关键。构造样本空间时尽量做到最优化，使得样本空间中的基本事件数最少，会给后面的概率计算带来更多的方便，起到事半功倍的效果［4］。

例4任取一非负整数，求该数的平方的个位数字是6的概率。

分析若将非负整数的全体作为样本空间，则是一个无限空间，不符合古典概型的第1个特征，变换一下思路便能很快找出另一个更加简单的样本空间。非负整数的平方的个位数字只取决于该数的个位数字，所以，可将非负整数的个位数字的取值，即0，1，2，3，4，5，6，7，8，9，作为样本空间，其基本事件总数n=10。

例5有n个人围绕一张圆桌而坐，求甲、乙两人相邻而坐的概率。

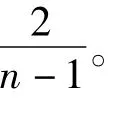
3.4 利用基本事件的有关性质

在古典概型中基本事件的发生是等可能的，势必出现许多对称和对等的问题［5-6］，如果能巧妙地加以运用，问题将变得异常简单且容易理解。

例6在线段AB上任取不同的3点P1，P2，P3，求P2位于P1与P3之间的概率。

分析此题若按常规方法去做有一定难度，但从对称性角度考虑就简单多了。设

M1=｛P1位于P2与P3之间｝，

M2=｛P2位于P1与P3之间｝，

M3=｛P3位于P1与P2之间｝，事件M1，M2，M3是对称的，其发生的可能性相等，且M1，M2，M3中任意两个事件是互斥的，则样本空间为｛M1，M2，M3｝，基本事件总数是3，所求事件概率

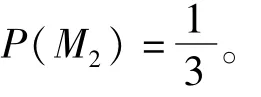
例7袋中有m只白球，n只黑球，现从中将球一一摸出（无放回），直至袋中剩下的球颜色都相同为止，求最后剩下的全是白球的概率。

分析如果先分别计算最后剩下1个，2个，…，m个白球的概率，再相加，其计算量将非常大。可以这样考虑，“最后剩下的全是白球”与“最后摸出的全是白球”是同一事件，而摸球共有m+n种可能，最后摸出白球有m种可能，从而摸出白球的概率是。

［1］何家顺.古典概型中样本空间的选取［J］.安庆师范学院学报：自然科学版，1998，3（3）：72-73.

［2］刘文斌.概率论与数理统计［M］.上海：同济大学出版社，2012：12-13.

［3］陈朝霞，杨雨慧.概率论中常见古典概型错题辨析［J］.南京工业职业技术学院学报，2004，4（3）：86-88.

［4］曾文建.古典概型中样本空间的选取［J］.福建商业高等专科学校学报，2007（3）：120-121.

［5］吴宏锷，梁瑛.优化样本空间，简化古典概型［J］.河南教育学院学报：自然科学版，2007，16（4）：12-13.

［6］张国俭.对等性在古典概型中的应用［J］.晋中学院学报，2009，6（3）：35-37.

〔责任编辑：卢 蕊〕

Determ ination of the total number of the basic events about the classical probability from solutions to a problem

WANG Hong-ping
（Basic Courses Teaching and Research Division，Jiangsu Judicial and Police Officer Higher Vocational School，Zhenjiang 212003，China）

The classical probability problem is one of the difficulties in one of the higher vocationalmathematics teaching，and how to determine the total number of basic events is the key to this kind of problem.There are two methods to determine the total number of basic events and so themethods are flexibly used for solutions to the problem.

classical probability；basic event；total number

G642

C

1008-8148（2014）04-0110-03

2014-05-09

王宏平（1965—），男，江苏东台人，讲师，主要从事高职数学教学研究。