履带行驶系统数学模型及张紧力计算
马星国,潘仕卫,尤小梅,叶 明,龚雪莲
履带行驶系统数学模型及张紧力计算
马星国1,潘仕卫1,尤小梅1,叶 明2,龚雪莲2
履带是履带行驶装置的重要部件之一。其功能是保证车辆在无路地面上的通过性,降低车辆的行驶阻力。它支撑负重轮并为其提供一条连续滚动的轨道。它通过与地面的作用,将地面的牵引力、附着力和地面制动力传给车体,使车辆能正常运动。履带张紧力对于履带行驶系统的性能有深刻影响。张紧力过大,履带刚度太大,起不到缓冲作用,会增加履带和底盘部件摩擦,能耗严重,并有断带危险;张紧力过小,使得履带松弛,容易脱带、耙齿,造成履带失效,车辆瘫痪。为提高车辆的综合性能,需要在各种行驶状况下给履带提供一个最佳的张紧力,因此张紧力的计算成为研究的重点。
Hub等[1]根据某履带车辆的模型,提出履带诱导轮附近张紧力的计算方法。Ma等[2]提出一种新的履带车辆负重轮与地面的作用的动力学模型,并且通过仿真验证其正确性。Park等[3]将低速履带环看成柔性带,通过建立履带的数学模型分析履带车辆的行驶性能。Al-Milli等[4]着重分析转向过程中履带与地面的作用机理,建立其数学模型,并且对干沙路面车辆通过性进行分析。本文分别对主动轮、负重轮以及诱导轮分别进行受力分析,最终得出各轮附近张紧力的表达式,为下一步控制履带张紧力奠定基础。
1 履带系统力学特性
履带车辆的履带系统包括主动轮、诱导轮、负重轮、托带轮和履带板组成,由83块履带板,5个负重轮,3个托带轮,主动轮、诱导轮以及张紧装置。图1从整体对履带系统进行受力分析,在分析计算时,将履带系统分成负重轮和诱导轮为二部分。

图1 履带行驶系统受力模型Fig.1 Mechanicalmodel for tracked vehicle
由于行驶过程各轮以及各轮曲臂惯性力及惯性力矩的量级远小于各轮周围张紧力,因此在此忽略不计。Ts1和Ts2是主动轮上、下支履带的张紧力,Ms为主动轮转矩,其关系为:

由于主动轮前置,忽略主动轮和诱导轮之间的履带板的重力和振动以及托带轮的影响时,可认为主动轮与诱导轮周围上支履带的张紧力Ts1与Ti1近似相等,主动轮下支履带张紧力Ts2与Tw1相等,诱导轮下支履带张紧力Ti1与Tw6近似相等,即为:

1.1 负重轮装置动力学模型
图1所示负重轮装置包括负重轮以及负重轮曲臂。第1,2,5轮采用扭杆加液压缓冲器的悬挂装置,3,4轮只使用扭杆悬挂装置。负重轮与曲臂计算模型最终推导出地面通过履带给负重轮的力。
1.1.1 负重轮曲臂动力学模型
负重轮曲臂主要受到车体通过旋转副给它的反力和力矩,以及负重轮通过旋转副给它的反力,由于忽略曲臂质量过小,忽略曲臂质量影响。如图2所示,曲臂绕P点的运动方程为:

式中:Mwai为曲臂绕P点转矩,Rwxi和Rwyi分别为负重轮对曲臂x和y方向作用力,lwai为P点与负重轮中心的距离。
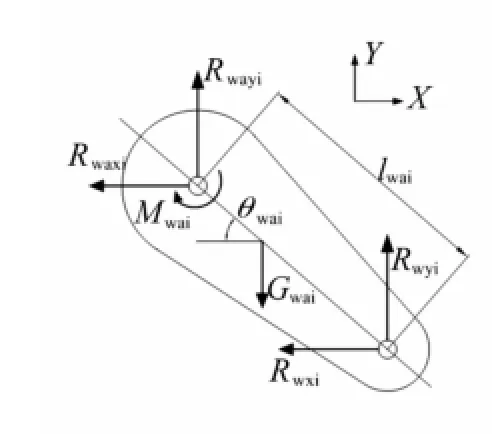
图2 负重轮曲臂力学模型Fig.2 Mechanical model forwheel arm
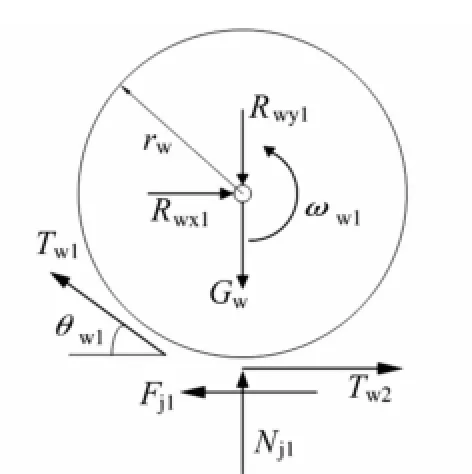
图3 第1负重轮力学模型Fig.3 Mechanical model for the wheel 1
1.1.2 负重轮周围张紧力计算
车辆运动过程中,每个负重轮都会与一个履带板接触。若将负重轮和与其接触的履带板看成一体,履带板质量过小,重力忽略不计。单侧负重轮共5个,第1与第5负重轮处的履带受力与地面成一定角度,因为需要将其单独分析,中间3个负重轮动力学特性一致,只需分析一个即可。
(1)第1负重轮动力学模型
如图3所示,负重轮受到曲臂通过旋转副给它的反力以及自身重力,与其接触的履带板受地面对其的法向作用力Nj1、两侧履带板给它的张紧力Tw1、Tw2以及牵引力Fj1,忽略负重轮相对车体加速度,可以列出动力学平衡方程:
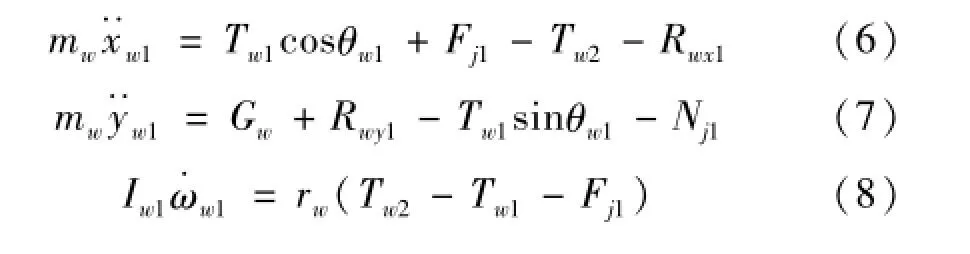
式中:Rwx1和Rwy1为曲臂对负重轮x和y方向作用力,Iw1是负重轮转动惯量,Gw为负重轮重力,rw为负重轮半径。
将方程(6)、(7)、(8)与方程(5)联立得:

(2)中间负重轮的动力学模型
中间三个负重轮受力情况如图4所示。负重轮受到曲臂通过旋转副给它的反力、负重轮重力,与其接触的履带板受到其两侧履带板给的张紧力Twi、Tw(i+1),地面对其法向作用力Nji以及牵引力Fji,动力学方程如下:

图4 中间负重轮力学模型Fig.4 Mechanicalmodel for themiddle wheels
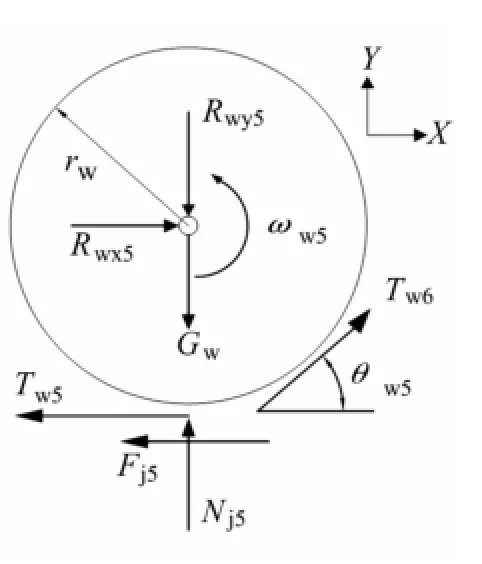
图5 第5负重轮力学模型Fig.5 Mechanical model for wheel 5
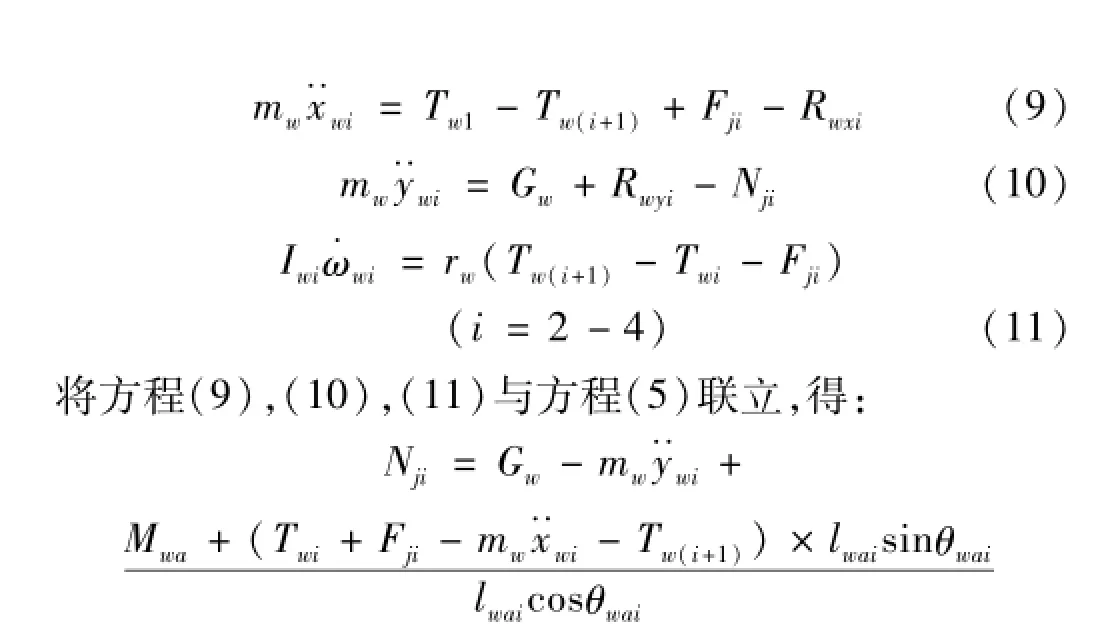
(3)第5负重轮的动力学模型
如图5所示,负重轮受到曲臂通过旋转副给它的反力、自身重力,与其接触的履带板受到两侧履带给的张紧力Tw5、Tw6,地面对其法向作用力Nj5以及牵引力Fj5,动力学方程如下:
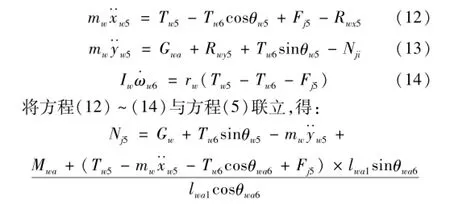
1.2 诱导轮周围张紧力的计算
诱导轮受到张紧装置和诱导轮曲臂支撑,结构如图6,曲臂上端与车体铰接于P0点,诱导轮与曲臂铰接于P1点,张紧装置一端与车体铰接于P3点,另一端与P2点连接。调整张紧力的过程是:张紧装置液压增加时,推动曲臂绕着P0点逆时针旋转,带动诱导轮旋转中心P1绕着P0向右上方移动,即为带动诱导轮后移,履带被拉伸,张紧力增加;反之,液压减小时,曲臂反向旋转,诱导轮前移,张紧力减小。影响诱导轮周围履带张紧力大小的主要因素:张紧装置对曲臂作用力、诱导轮两侧履带角度的变化、曲臂的角度变化以及诱导轮运动等。
1.2.1 诱导轮动力学模型
图6所示由于诱导轮周围履带板质量很小,在此忽略履带板质量影响。诱导轮上支履带受张紧力Ti1,其与水平方向夹角θ1;下支履带受张紧力Ti2,其与竖直方向夹角为θ2,计算方程如下:

式中:Fce为诱导轮周围履带旋转的离心合力,与水平夹角θce,旋转副P1对诱导轮的作用力为Rix和Riy,诱导轮重力为Gi,Ii为诱导轮转动惯量,半径为ri。
进一步推广式(27),对于ω条交点轴线的公差累积,设第τ条交点轴线的圆柱域为2Tτ,τ=1,2,,ω,则沿Q和Lv方向的累积公差tQ和tLv为:
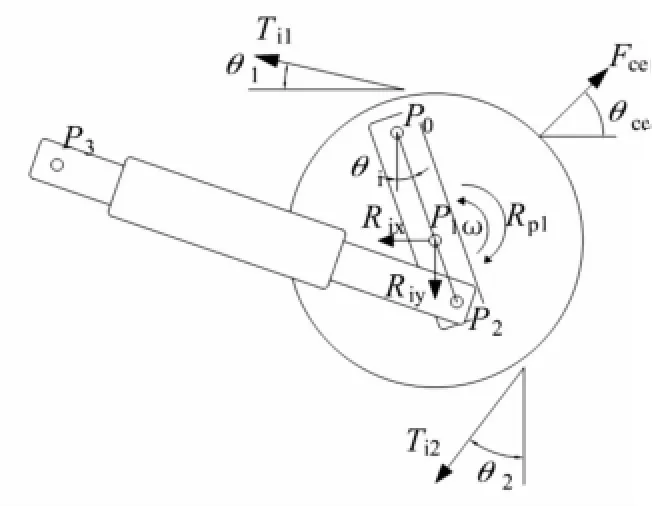
图6 诱导轮受力分析Fig.6 Mechanicalmodel for idler
忽略车辆的滑移和滑转,诱导轮的角速度为ωi,单位质量为ρ,Fce和θce的计算公式为:
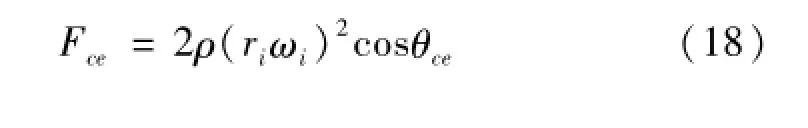

诱导轮与其附近托带轮以及负重轮的几何关系如图7所示,通过分析,得到θ和θ的计算关系式:

式中:rr为托带轮半径,lΔx1与lΔy1为P0与P6的x与y向距离,l1为P0到P1距离。

式中:lΔx3和lΔy3为P1与P4点x和y向距离,lΔx2和lΔy2为P1与P5点x和y向距离。
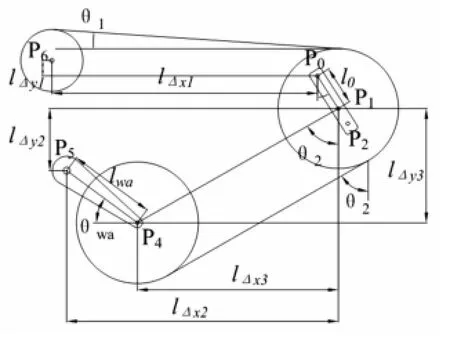
图7 负重轮、拖带轮、诱导轮位置关系Fig.7 Relation between wheel,roller and idler
1.2.2 诱导轮曲臂力学模型

图8 诱导轮曲臂受力分析Fig.8 Mechanicalmodel for idler arm
如图8所示,曲臂主要受诱导轮通过旋转副给它的反力,车体通过旋转副给它的反力,张紧装置给它的作用力Ftt,曲臂绕P0点的运动方程为:


式中可以看出,诱导轮处张紧力不管处于任何工况下只与诱导轮的角速度、加速度、曲臂转角、张紧装置压力和长度有关。这些变量可以直接从履带车辆整车的动力学仿真中得到。由方程(2)、(1)、(3)、(4),可以分别求出Ts2、Ts1、Tw6、Tw1。车辆行驶的牵引力Fji可以求出,因此Twi都可以求出。履带与地面接触力Nji只与负重轮加速度、负重轮曲臂摆角、牵引力和两侧履带张紧力有关,同样这些力也可以从动力学仿真得到。
2 公式计算和软件仿真的结果对比
在多体动力学软件Recudyn中使用Track(HM)建立履带车辆的动力学模型,共有166块履带板,整车共有1162个自由度。通过多体动力学模型,可以使用Recurdyn软件可以测得不同工况下诱导轮的角速度、加速度、曲臂转角、张紧装置压力等值,将变量值代入Ti1,即得到不同工况下Ti1,同理可以得到Nij曲线,可以与Recurdyn中仿真结果进行对比验证,来验证计算的准确性。
2.1 平路直行
2.1.1 诱导轮张紧力Ti1对比
在平坦路面上,选用干沙与坚实两种土壤,车辆在0~5 s内在自身重力作用下落至水平路面,在减震器作用下迅速吸振后处于水平静止状态;在5~8 s内车辆开始加速,由0 km/h加速到20 km/h。图9和10分别是车辆在坚实和干沙行驶时诱导轮处张紧力曲线对比图。可以看出,坚实路面行驶时,在加速阶段,主动轮力矩增大,上支履带张紧,所以诱导轮周围张紧力有个明显上升趋势,然后受到张紧装置调整,张紧力又开始降低,最后加速过程结束后,车辆均速行驶后,张紧力变化趋于稳定;干沙也同坚实规律基本相同,不过由于受到地面影响,车辆在干沙路面行驶稳定性弱,导致干沙路面张紧力波动幅值大,峰值大。计算曲线可以看出,加速过程中主动轮力矩作用,张紧力先加后减,加速结束后,张紧力变化较小,因为计算分析忽略惯性以及履带板与诱导轮瞬时碰撞的因素,所以没有突出的峰值,计算曲线与仿真曲线规律大致相同。
2.1.2 负重轮与地面法向力
如图11、12所示为负重轮与地面法向力的仿真与计算曲线,任意一块履带板沿着履带环转一周,它与5个负重轮依次接触一次,图中可以清楚看出5个峰值为一组,并且按着负重轮1~5排列,不管坚实路面还是干沙路面,第1,2,5轮处接触力的值要大于其他的值,是由于第1,2负重轮处于履带前端,行驶中受到地面冲击作用大;第5负重轮处于履带环尾部,同样受到冲击较大,并且受到诱导轮下支履带张紧力的作用,所以其与地面接触力较大。由于公式推导中忽略由于地面激励产生的振动冲击作用,所以在第5负重轮处接触力同样较大,两者变化规律完全相符,因此公式准确度较高。

图9 坚实路面直行Ti1曲线Fig.9 Comparison of force Ti1on solid road
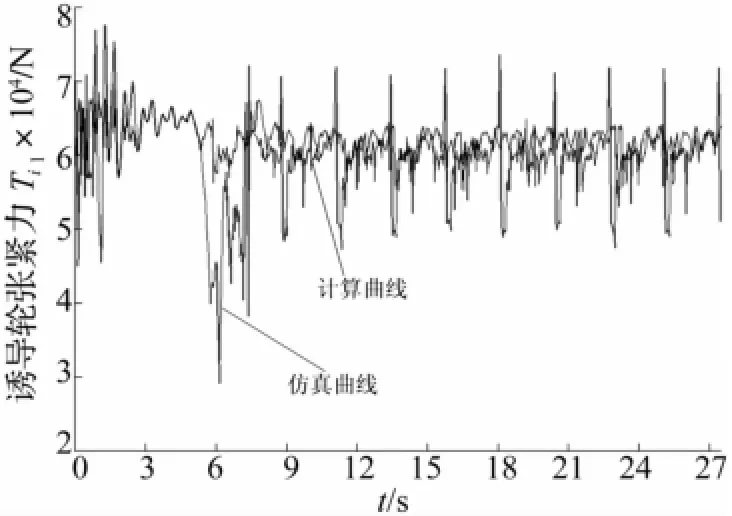
图10 干沙路面直行Ti1曲线Fig.10 Comparison of force Ti1on sand road

图11 坚实路面直行Nji曲线Fig.11 Comparison of force Njion solid road

图12 干沙路面直行Nji曲线Fig.12 Comparison of force Njion sand road
2.2 平路转弯
车辆在平坦路面上,同样是干沙与坚实两种土壤,车辆在0~5 s内在自身重力作用下落至水平路面,在减震器作用下迅速吸振后处于水平静止状态;在5~8 s内从0 km/h加速到20 km/h,左侧履带保持速度不变,右侧履带速度从20 km/h减到-18 km/h,图13、14为坚实路面转向时左右两侧履带张紧力曲线。坚实路面转向时,两侧履带都受到力矩作用,在右侧履带减速之后,左侧主动轮维持之前速度不变,两侧履带所受力矩左侧大于右侧,所以左侧履带张紧力较大,右侧履带张紧力较小。张紧力计算结果仍然与仿真结果大致相同,只是计算结果变化幅度小,由于计算公式忽略惯性影响,以及地面冲击作用,所以其值波动较小,相对平稳。图15、16为干沙路面转向时左右两侧履带张紧力曲线。干沙路面因为干沙路面影响,张紧力的值以及变化范围稍大于坚实路面,但是其变化规律与坚实路面一样。

图13 坚实路面转向左侧Ti1曲线Fig.13 Comparison of left track force Ti1steering on solid surface
3 结 论
(1)根据仿真曲线与计算曲线的对比,可知论文推导建立的公式可以反映履带张紧力变化规律,其结果与仿真结果符合度高。由此可知,论文建立的履带张紧力的数学公式是正确的。
(2)任意工况下,通过得到的角速度、加速度、曲臂转角、张紧装置压力和长度等数据,代入公式,可以求出诱导轮周围履带板张紧力的值。通过诱导轮周围张紧力可以求出履带主动轮、负重轮处张紧力,也可以求出负重轮与地面的接触力及整个履带的受力等。
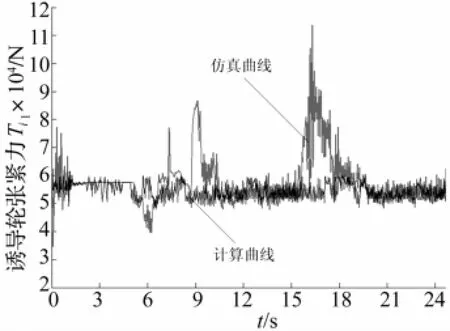
图14 坚实路面转向右侧Ti1曲线Fig.14 Comparison of right track force Ti1steering on solid surface
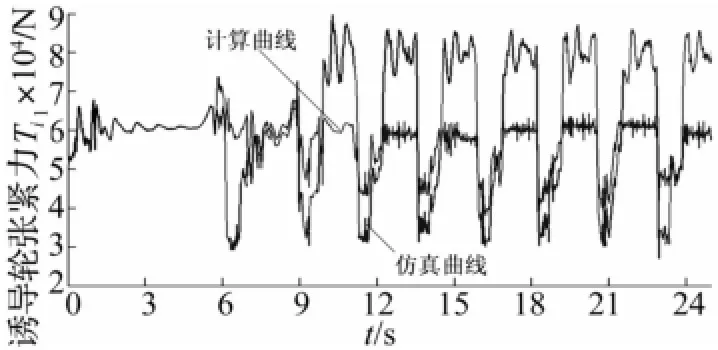
图15 干沙路面转向左侧Ti1曲线Fig.15 Comparison of left track force Njisteering on sand surface

图16 干沙路面转向右侧Ti1曲线Fig.16 Comparison of rightforce Njisteering on sand surface
[1]Hub K,Cho B H.Development of a track tension monitoring system in tracked vehicles on flat ground[J].Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering,2001,215(5):567-578.
[2]Ma ZD,Perkins N C.A track wheel terrain interactionmodel for dynamic simulation of tracked vehicles[J].Vehicle System Dynamics,2002,37(6):401-421.
[3]Park W Y,Chang Y C,Lee S S.Prediction of the tractive performance of a flexible tracked vehicle[J].Journal of Terramechanics,2008,45:13-23.
[4]A l-Milli S,Seneviratne L D,Althoefer K.Track-terrain modeling and traversability prediction for tracked vehicles on soft terrain[J].Journal of Terramechanics,2010,47:151-160.
(1.沈阳理工大学机械工程学院,沈阳 110159;2.北京北方车辆集团有限公司,北京 100072)
根据高速履带车辆履带系统的结构,分析履带系统各部分受力,建立负重轮及其曲臂、诱导轮及其曲臂的数学模型,得到履带系统各部位的张紧力以及地面对负重轮法向力的计算公式。建立Recurdyn整车动力学模型,进行多工况下的仿真,得到履带张紧力、以及负重轮法向力的仿真结果,将仿真与公式计算结果相对比,结果表明:公式计算结果与RecurDyn仿真结果具有很好的符合度,验证了公式的准确性。本研究结果为履带行驶系统张紧力的控制奠定了基础。
履带车辆;张紧力;动力学模型
Mathematicalmodels for a caterpillar driving system and its tension calculation
MA Xing-guo1,PAN Shi-wei1,YOU Xiao-mei1,YEMing2,GONG Xue-lian2
(1.Shenyang Ligong University,Shenyang 110159,China;2.Beijing North Vehicle Group Corporation,Beijing100072,China)
According to the structure of a tracked system in tracked vehicles,the forces acting on componentsof the tracked system were analyzed and mathematicalmodels for componentswere established.The formulas for track tensions and normal forces between wheels and ground were derived with themathematicalmodels,and the formulas were verified by comparing the calculated resultswith the formulas to the simulation resultswith Recurdyn dynamcimodel.The formulas provided a theoretical basis for control of tensions of a tracked system.
tracked vehicle;tension;dynamic model
TH212;TH213.3
A
2013-01-06 修改稿收到日期:2013-03-11
马星国男,博士,教授,1963年2月生

