船舶搁浅于台型礁石场景下双层底纵桁上纵骨变形机理研究

于兆龙，胡志强，2，王 革，姜 哲

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.大连理工大学工业装备结构分析国家重点实验室，大连 116023；3.美国船级社，新加坡；4.中国海洋石油总公司研究总院，北京）

船舶搁浅于台型礁石场景下双层底纵桁上纵骨变形机理研究

于兆龙1，胡志强1，2，王 革3，姜 哲4

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.大连理工大学工业装备结构分析国家重点实验室，大连 116023；3.美国船级社，新加坡；4.中国海洋石油总公司研究总院，北京）

以典型船舶双层底结构中纵桁上的纵骨为研究对象，运用塑性力学理论和数值仿真手段，讨论了纵桁上骨材在船舶搁浅于台型礁石场景下的变形过程和破坏机理。研究中应用LS＿DYNA仿真模拟得到结构变形模态和能量耗散结果，在研究变形模态基础上建立底纵桁骨材塑性变形发展过程的数学模型。运用塑性力学理论求解纵桁上骨材变形吸收的结构变形能和平均变形阻力；同时，应用数值仿真结果进行验证。研究得到的纵桁骨材变形阻力和变形能解析计算公式，对船舶双层底耐撞性结构设计和耐撞性能评估都具有一定的指导意义。

船舶搁浅；底纵桁骨材；解析计算；数值仿真；结构变形能

近几十年来伴随着海上航行的船舶数量不断增加，船舶搁浅、触礁和碰撞事故的发生也愈发频繁。严重的船舶碰撞与搁浅事故会造成巨大的经济损失和人员伤亡，同时还会引发环境污染等生态灾难，最为著名的是1989年发生在美国阿拉斯加的Exxon Valdez号油轮搁浅事故，引发大量的原油泄漏，成为人类海运史上最具破坏性的人造生态灾难。为了将船舶因此类碰撞和搁浅造成的损失降到最低，船舶设计中需要针对船舶抗撞性能提出更多的理性设计标准来评估船舶安全性能。为此，研究人员［1］在评估船舶结构响应上投入了大量的研究工作，提出很多创新性的概念和方法，并最终应用于船舶初步设计当中。

评估船体结构响应的方法主要有四种：简化解析法，模型试验，实船实验和数值仿真。其中简化解析法具有计算周期短、结构变形破坏模态易观察、结果精度较高等优点，适合应用于船舶初步设计和碰撞事故应急处理。简化解析法的提出一般是基于实船事故、模型试验和数值仿真得到的破坏变形模态建立的。破坏变形模态很大程度上和礁石的形状相关［2］，其中对台形礁石研究相对较少。Hong等［3］提出一种油轮搁浅于台型礁石时双层底板材构件（纵桁、肋板和外底板）变形模态的数学模型并给出其结构变形能解析式。该方法对船舶触礁搁浅事故紧急处理和船舶防撞性设计具有一定的意义。然而，该方法中并没有考虑相关骨材的作用。骨材构件通过与板材构件焊接为一个整体从而提高结构整体的强度和刚度。传统的处理骨材的方法是Paik［4］提出的等效板厚法，即将骨材截面分摊到被依附的板上，通过被依附板的厚度的增加来代替骨材的作用，这一方法可以粗略的估算骨材的作用。然而，Hu等［5］通过研究证明在船舶搁浅于台型礁石时，这种方法明显低估了骨材的作用，其后刘毅等［6］针对这一问题运用数值方法确定了等效板厚法在台型礁石搁浅时的有效系数，不过这种方法还是不能从本质上解决问题。因此，本文通过对数值模拟的变形模态进行分析，运用塑性理论对双层底纵桁上骨材的变形模态和破坏机理进行研究，得到骨材变形能和变形阻力解析计算公式，并通过数值仿真结果验证，所得到的结论对搁浅场景下船舶耐撞性结构设计和船舶的耐撞性能评估都具有一定的指导意义。

1 问题描述

Hong等［3］给出了在不考虑骨材情况下，船舶搁浅于台型礁石时双层底结构的变形模态和结构响应的解析式。然而，对于真实船舶，骨材显著地增加了结构刚度从而帮助抵抗外载荷的作用。典型的油轮双层底结构（带骨材）如图1所示，主要包括3部分：外底板、船底纵桁和肋板，撞击情景如图1所示。

图1 典型油轮双层底结构及撞击场景示意图Fig.1 A typical double bottom structure with stiffeners

本文研究纵桁上的骨材在双层底油轮搁浅于台型礁石场景下的结构响应。纵桁上骨材的布置如图2所示，沿着纵桁高度方向均匀的布置3根纵骨由下到上分别编号为1、2、3，且撞深的增加方向设定为自下而上，即礁石首先接触到第1号纵骨。同一根纵桁上的一组骨材在搁浅之后的变形模态如图3（a），其中撞击深度取为0.7Hb（Hb为双层底高度）。由图3可见纵桁上的纵骨具有稳定的变形特征，变形曲线呈振荡的弧形状，同时具有明显的周期性。不同位置的骨材周期相同，但是相位有差异。由图3（b）可以看到对称布置的1号和3号骨材在0.7Hb撞深下具有相似的相位。然而由图3（c），1号与2号骨材具有明显的相位差，但振幅基本保持一致。

图2 纵桁上骨材布置图Fig.2 The arrangement of longitudinal girder attached tiffeners

图3 纵桁骨材变形模态示意图Fig.3 The deformation patterns

图4中给出了纵桁上骨材形成弧形的变形模态的过程。由图4可见，礁石将骨材挤压到撞深附近的位置，从而使骨材与未变形的骨材形成一个倾斜的角度。从未变形到被挤压到撞击深度的位置，骨材承受强烈的拉伸和弯曲变形，形成最终的弧状变形。这种倾斜的弧状变形模式使得同一种撞击深度下不同垂向位置的骨材在完全与礁石撞击发生变形时，变形的最大横向延伸趋于相近。

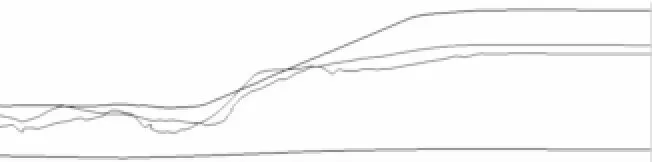
图4 纵桁上骨材弧状变形的形成（轮廓模式）Fig.4 The arch-shaped deformation of longitudinal girder stiffeners（edgemode）

现有的船底纵桁构件搁浅于台型礁石的理论模型的提出都是仅针对有带板的纵桁单独作用的情况，并没有考虑肋板的影响。本文研究针对整个双层底结构中的纵桁和骨材，因而需要考虑双层底结构之间的相互作用对变形结果的影响。纵桁与肋板组成的交叉构件明显增强了交叉点处局部的强度和刚度，对纵桁的变形周期影响比较明显。通过对LS＿DYNA数值仿真的变形结果进行测量并取平均值，示于表1，其中在模型中肋板间距l＝4 m。

表1 数值仿真中纵桁的变形周期结果Tab.1 The deformation cycle length of longitudinal girders in num erical simulations

表1中算例一栏的含义如下：工况“20＿5”是指礁石角度为20°，撞击深度与双层底高度比为0.5的算例，本文其他工况号也应用这一定义。由表1可知，尽管周期随礁石角度和撞击深度变化仍呈现一定规律，但纵桁与肋板的交叉结构很大程度的减弱了这种变化规律产生的效果，不同撞深不同角度的周期都趋向于相邻肋板之间的距离。故在理论模型中假设由于交叉结构的影响，变形周期不随角度和撞深变化，即：

Lc＝2L＝l（1）

2 研究现状分析及理论模型的提出

2.1 研究现状

关于船舶搁浅于台型礁石情况下的双层底结构骨材的变形模式和能量耗散的相关研究较少。传统的方法是依照Paik［4］的等效板厚法近似估算，但结果精度较差。本文从机理上着手对纵桁上骨材结构变形响应进行解析研究。骨材的变形和破坏很大程度上受到其所依附板材的变形影响。Amdahl［7］给出了肋板与纵桁组成的交叉结构在轴向载荷作用下的两种响应模式：对称模态和非对称模态。Simonsen［8］针对船舶搁浅于圆锥形礁石情景下提出了一种移动的变形区域理论，并给出了以薄膜拉伸为主要模式的能量耗散解析式。Midtun等［9］对船舶搁浅于台型礁石情况下纵桁变形和响应进行机理解析，但是其给出的解析式具有不小的局限性，没有给出变形角度和周期的解析解，而是根据数值仿真结果拟合得出，其是否适用于不同结构尺寸下的响应估计仍然需要进一步验证。Hong等［1］在此基础上进一步研究并提出了一种新的纵桁在台型礁石搁浅情景下的变形和破坏模式并给出解析解，其变形模态及理论模型如图5所示。其中，2L为纵桁水平方向的变形周期长度，θ为横向变形角，2H为垂向挤压深度，M为边ab在变形后产生的纵向滑移距离。

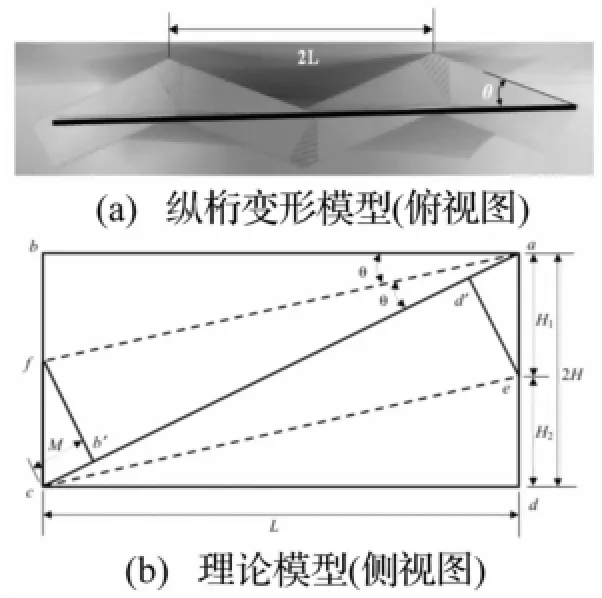
图5 Hong和Amdahl的纵桁变形的理论模型Fig.5 Hong and Amdahl's theoretical model of longitudinal girders

2.2 Hong和Am dah l的纵桁模型中存在的问题

在Hong和Amdahl［1］的模型中，以一条直线代表纵桁上的骨材（如图6左所示），变形后结果见图6右，其中斜线阴影处为膜拉伸能量耗散区域。根据其模型理论，尽管纵桁变形呈周期性振荡，但骨材变形后仍保持为直线，这并不符合在数值仿真中观察到的变形结果。同时，Midtun和Amdahl［9］应用数值仿真技术证明了肋板的存在不会影响纵桁变形最大的横向伸展程度，而只会限制靠近肋板与纵桁交叉处的横向变形程度。基于这一结果，对数值仿真结果的纵桁横向变形测量结果对比，以26.5°为例，结果如表2所示。

图6 纸折法表示Hong和Amdahl的加筋纵桁梁的变形模型Fig.6 Hong and Amdahl's stiffened longitudinal girder deformationmodel by paper folding

由表2可知，数值仿真结果随撞深增加，横向变形延伸并没有非常明显的增大趋势，增长趋势缓慢。因此，Hong和Amdahl的台型礁石搁浅场景下的纵桁模型的最大横向伸展距离在很大程度上高估了真实的横向延伸情况，故该理论模型需要进一步改进。

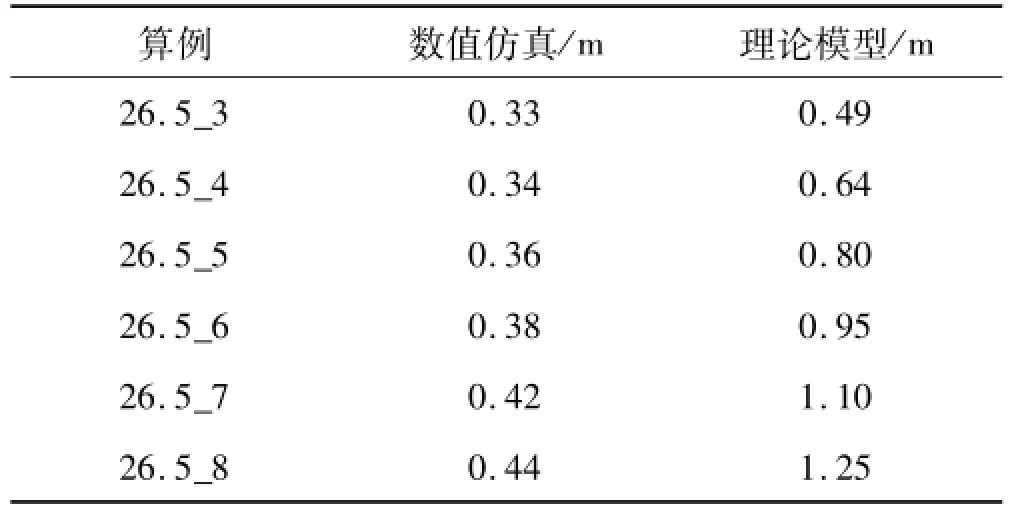
表2 Hong和Am dahl的纵桁模型横向延伸量的数值对比Tab.2 Transverse extent verification of Hong and Amdahl's longitudinal girder model by numerical simu lations

2.3 新纵桁理论模型的提出

基于以上分析，提出一种新的纵桁变形理论模型，如图7所示。

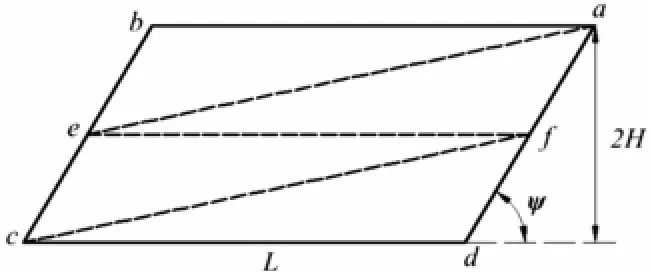
图7 台型礁石搁浅情景中一种新的纵桁理论模型Fig.7 A new theoreticalmodel for longitudinal girders during shoal grounding scenario

在新的纵桁变形模型中，纵桁板被ef分为变形模式相同的上下两部分。塑性绞线ae、cf呈弧形状，分别弯向纵桁板平面的两侧，这符合数值仿真中横截面的观察结果，如图8所示。

图8 典型纵桁截面的变形过程Fig.8 Folding process of a typical cross section of the girder

图8中E点对应着图7中的折痕ef，ef也是一条振荡曲线，与上下两部分的折痕相位相差π／2，图8中的E点为其正好振荡到平衡位置。这一结论可以图3中得到证实。

新纵桁模型的横向伸展的数值和理论结果对比如表3，数值结果显示随着撞深每增加0.1Hm＝0.268，横向变形伸展仅增加0.02 m，这充分说明垂向的变形初始为2个对称模态，但并不局限于两个近似的对称模态，而随着撞深的增加可能存在更多的模态。即当撞深增加到一定程度设为2H0时，横向延伸不再增加，而是在垂向开始了另一个新的垂向变形周期。

表3 新纵桁板材模型横向延伸距离的数值对比验证Tab.3 Transverse extentvalidation of the new longitudinal girder model by numerical simulations

基于这一新的纵桁理论模型，可以得到纵桁骨材的最大的横向伸展距离为：

撞深和礁石角度影响公式，可以采用Hong和Amdahl的模型中计算公式：

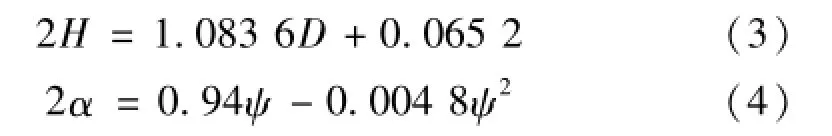
其中：D为撞击深度，ψ为礁石的角度。

3 纵桁的纵骨变形机理解析计算

图3中给出了纵桁上骨材在台型礁石搁浅中的变形模态，通过数值模拟结果的观察分析发现骨材的变形可分为两种：与礁石完全接触的纵骨碰撞变形和尚未接触礁石产生的波及变形。本文旨在详细阐述纵骨完全碰撞情况下的变形机理，其能量耗散方式主要有三种：

（1）纵骨弧形状变形的弯曲能量

（2）纵骨弧形状变形的膜拉伸能量

（3）纵骨在垂向被礁石挤压弯曲的能量

三种能量耗散方式在下面做详细阐述。传统的金属在变形做功过程中会发生硬化现象，流动应力会大于初始屈服应力σy小于极限抗拉强度σu，因此取流动应力σ0＝（σy＋σu）／2［10］。从能量耗散模式上来看，耗散模式主要有两种即弯曲能量Eb和膜拉伸能量Em。

N0＝σ0A（8）

其中：σ0为流动应力，ε·eq为等效应变率，为主应变率。和l分别为经过第i根塑性绞线的角速度和第i根绞线的长度。

3.1 与礁石完全接触的纵骨变形机理

根据数值仿真结果的观察和新纵桁模型理论，提出如图9中所示的半个周期的纵骨骨材变形理论模型。圆柱形的外轮廓保证在不同位置上骨材的最大横向延伸变形相同。纵骨变形呈螺旋状上升，螺旋倾角为α。

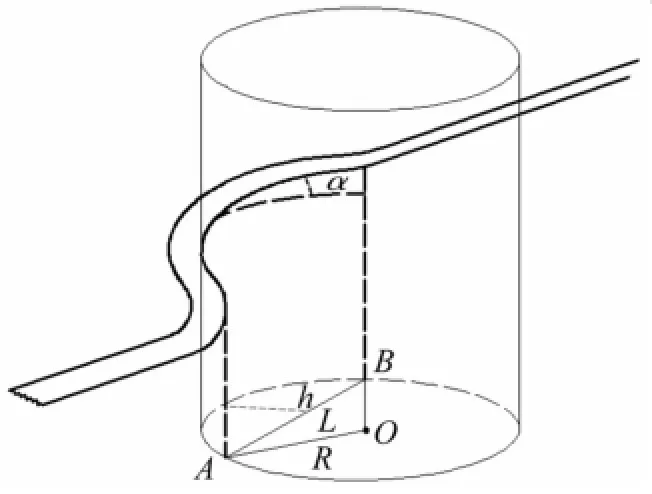
图9 纵骨变形理论模型Fig.9 Theoreticalmodel of the deformed stiffener

如图9所示，骨材AB原长为L，拱形的高位h，则有：

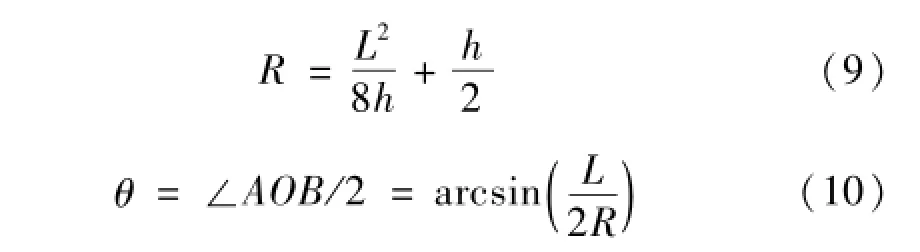
由于倾斜的骨材弧形变形对应的为椭圆形状，为方便计算弯曲能量这里采用圆形近似其圆心角用∠AOB相似（由于膜拉伸为最主要的能量耗散方式，这一近似计算得到的弯曲能量对整体影响不大）。经过塑性变形后骨材由于拉伸而变长，则骨材伸长长度为：

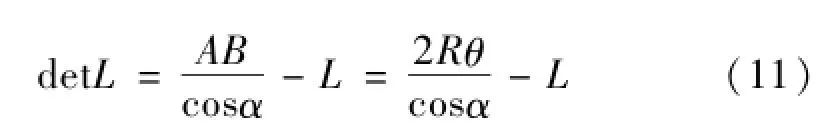
则圆弧变形的膜拉伸能量为：

圆弧变形的弯曲能量为：

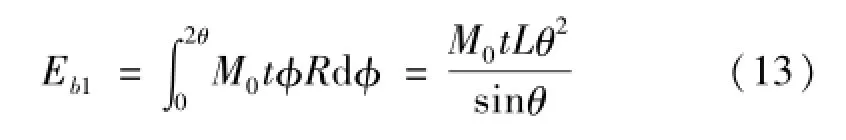
其中t为骨材的厚度。

图9中讨论的是半个周期内的纵骨变形，但从局部来看，由于礁石挤压引起纵骨垂直方向上产生的位移是紧贴礁石前壁的，因而形成的局部垂向弯曲角度即为礁石角度φ，其弯曲能量为：

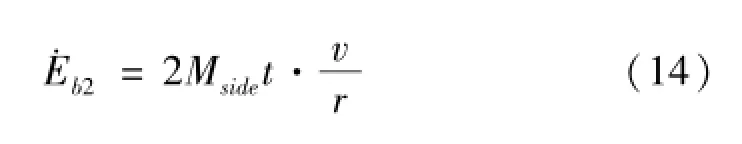
其中Mside＝σ0t2／4，对于r的取值参见Yu等［11］得：r＝1／ψ，则对于半周期：

Eb2＝2MsidetLψ（15）

综上半周期内纵骨耗散的能量为：

EL＝Eb1＋Eb2＋Em（16）

3.2 碰撞力

基于变形分析和塑性理论已经建立了纵桁纵骨在两种情况下的能量耗散解析式。能量吸收主要由水平力和垂直力共同做功。水平内力FH，plasticity（塑性水平力）和垂直内力FV，plasticity（塑性垂直力）与礁石角度直接相关，如图10，表达式如下：

图10 礁石受力情况Fig.10 Grounding resistances on the indenter（Hong 2011）

水平方向基于力的平衡，FH得到：

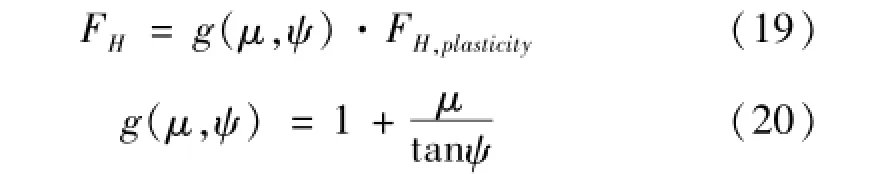
参数g（μ，ψ）最先由Ohtsubo等［12］提出，用来计算船底板撕裂时的摩擦效应。然后，可得FV：

其中：FH和FV分别为水平力和垂直力。

4 数值仿真验证模型

4.1 模型描述

本文以一艘140 000 t穿梭油轮平行中体的一个分段作为研究对象，进行双层底结构数值仿真研究。其侧视图见图11，油船主要结构尺寸见表4。搁浅的场景如图1所示，礁石为具有较大的接触面积，截面为梯形的台型礁石。这类礁石与传统的有尖锐棱角的礁石相比，不会造成结构或板的撕裂，却更容易通过使结构发生变形从而降低整体的抗弯刚度和强度，因此值得深入研究［3］。

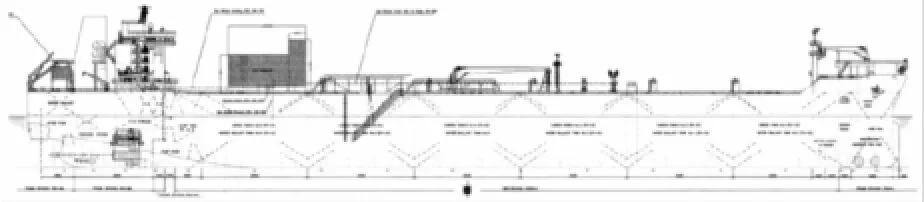
图11 油船型线的侧视图Fig.11 A side view of the tanker

表4 油轮的主尺度Tab.4 Scantlings of the shutter tanker

4.2 有限元模型及仿真算例

数值仿真过程采用PATRAN2008r2进行船体舱段建模并应用非线性动力学软件LS＿DYNA971进行计算。油船的有限元模型如图12所示，该舱段模型主要采用了四边形Belytschko7－Tsay（ELFORM2）单元，模型共划分了299 586个单元。舱段模型纵向延伸到两个横舱壁处，横向连接舷侧外板，因此舱段的内部结构有足够大的空间在礁石模型的撞击中发生完整稳定的变形［13］。为了提高计算精度和效率，有限元模型网格疏密结合。对可能发生接触的双层底区域精细模拟，其它区域为粗网格，并由细网格部分逐渐过渡到粗网格部分。为了研究不同垂向高度下的纵桁骨材吸收能量的情况，不同高度骨材被分开成不同的部分并编号如图2。

图12 双层底油船的有限元模型Fig.12 Finite elementmodel of the double bottom tanker

舱段模型在两端固定并忽略船体运动的影响，通过礁石模型移动完成搁浅模拟。搁浅过程中结构采用自接触和主从接触相结合。摩擦系数取为0.3，纵桁的高度即双层底的高度为Hb＝2.68 m，板厚为20 mm；相应的纵桁上的骨材高度为h＝250 mm，厚度为t＝10 mm。

为了全面地对提出的解析方法进行验证，数值仿真计算涵盖较广的礁石角度和不同的撞击深度。因为海底障碍物为台型礁石，所以礁石的角度不应太大（否则礁石会变为尖锐棱角状，产生撕裂，从而不适用本方法）。从保守角度来考虑，礁石的角度分别选取为20°，26.5°，45°和60°，对应于每一个礁石角度，选取10%Hb－90%Hb的双层底高度进行验证。

5 数值仿真验证结果和讨论

5.1 数值仿真结果与分析

本文采用数值仿真技术对提出的纵桁纵骨在台型礁石搁浅场景下的理论模型进行验证和讨论。表5中列出了同一根纵桁上的3根处于不同高度的骨材能量耗散的数值仿真结果。

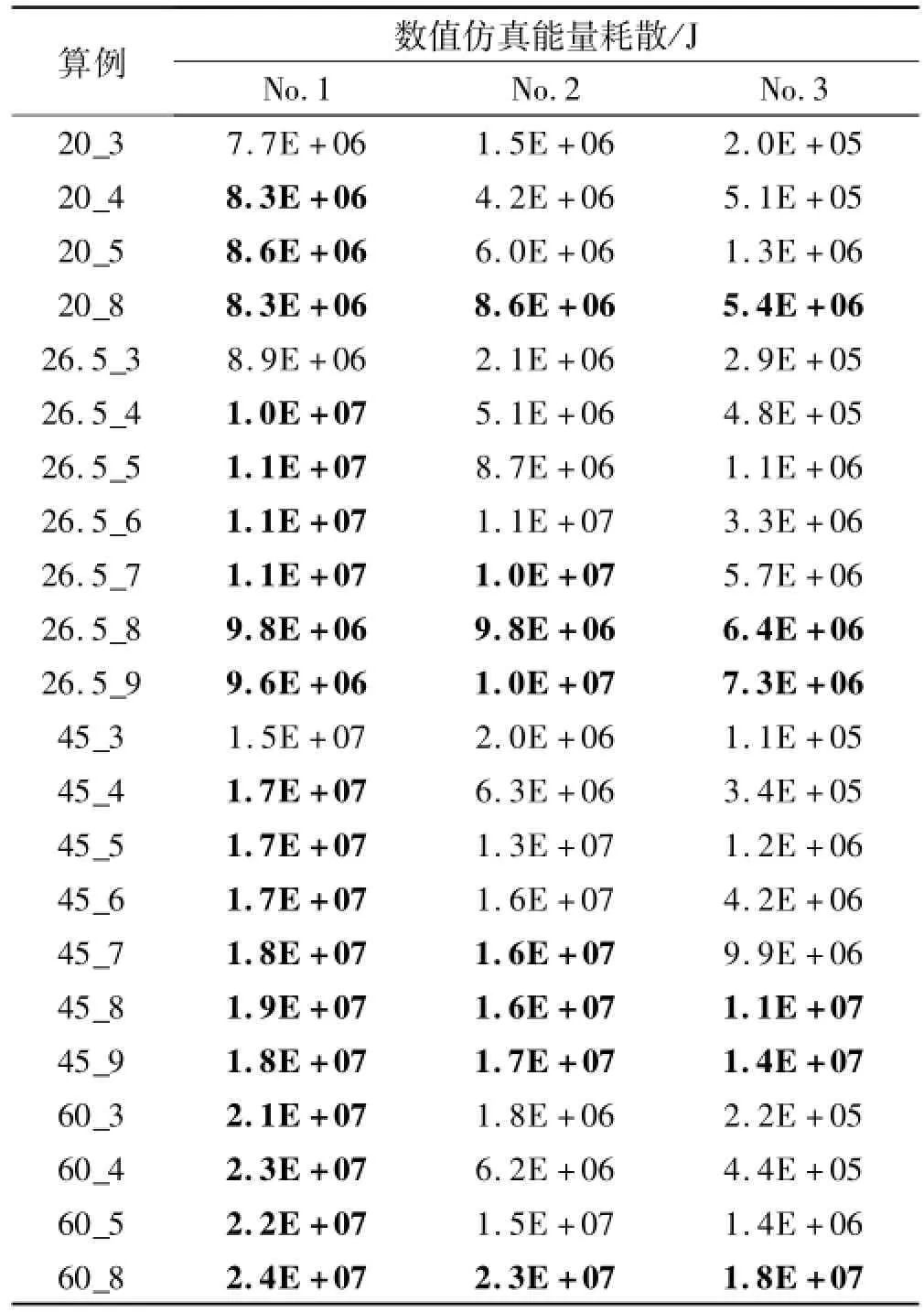
表5 同一纵桁上3根骨材的能量耗散数值仿真结果Tab.5Numerical energy dissipation of three different stiffeners in vertical direction on a girder

表5中加粗的数字表示与礁石完全接触变形的纵骨能量，未加粗的数字为波及变形产生的纵骨能量。可见，1号纵骨变形能量基本上为纵骨完全接触变形产生的，2、3号纵骨变形大部分为未接触礁石而由能量传递产生的波及变形产生的。由1号纵骨变形能结果可见，骨材在同一角度不同撞深时的能量耗散变化趋势不明显。小撞深时，随撞深增加而纵骨能量增加，当增加到一定程度时，撞深继续增加而能量反而有减小的趋势。但总体来说能量变化不大，基本稳定在一个值附近。观察0.8Hb，0.9Hb情况下三种纵骨都达到完全接触变性，同一角度下三者的值比较接近，第三号纵骨变形值略小。这主要是由于垂向新的变形周期尚未完全形成，横向伸展尚未达到最大。

纵桁的纵骨中有一些并未与礁石发生直接接触，但由于纵桁变形的能量传递效应，这类纵骨也会发生间接变形。图13中给出了算例45＿5中三种不同高度下的骨材能量耗散随撞深的变化趋势。

图13 45＿5中三根不同位置纵骨数值能量－变形长度曲线Fig.13 Numerical energy dissipation-crushing length curves of three vertically different stiffeners for case 45＿5

由上图可见，骨材由于能量传递产生的波及变形，其能量耗散与完全碰撞下模态相同，仍保持线性变化。由图3观察可得二者的变形周期亦保持一致。唯一的区别是变形的横向最大伸展在不断缩小，因其整体能量减小，如表5所示。波及变形的能量耗散详细变形机理有待进一步研究。

5.2 纵骨理论公式数值验证

图7中的新的纵桁变形模型上下对称，然而随着撞深的增加，在垂直方向上还可能会出现更多的变形周期，因而H0的取值很重要。以上理论不能给出H0的闭式解析解，基于数值仿真给出经验解为：

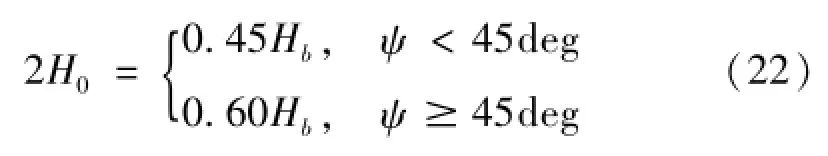
当D＜＝2H0时，直接代入理论公式求解。当撞深增加到D＞2H0时，应将D换算到2H0范围之内，再代入理论公式，具体换算方法如下：设Hs为纵骨由下而上的垂向高度位置，当D－Hs＜H0时，则2H＝H0＋D－Hs；当D－Hs≥H0时，则说明该纵骨跨越至少两个不同垂向变形周期的纵骨，其横向伸展必然会达到最大值，则整体的变形的能量将不再发生变化，此时即2H＝2H0。根据以上说明得到理论解和数值解的对比结果如表6所示。

其中误差的定义为：

误差＝（E理论－E数值）／E数值×100%（23）

由表6可见，不同垂向位置的纵骨的理论模型能量耗散结果与数值仿真的接过符合情况良好：能量误差大部分处于±10%以内，最大误差不超过30%。在图14给出了算例45＿5中1号骨材完全接触下的能量耗散曲线的数值仿真与理论计算数值随撞深变化的情况。

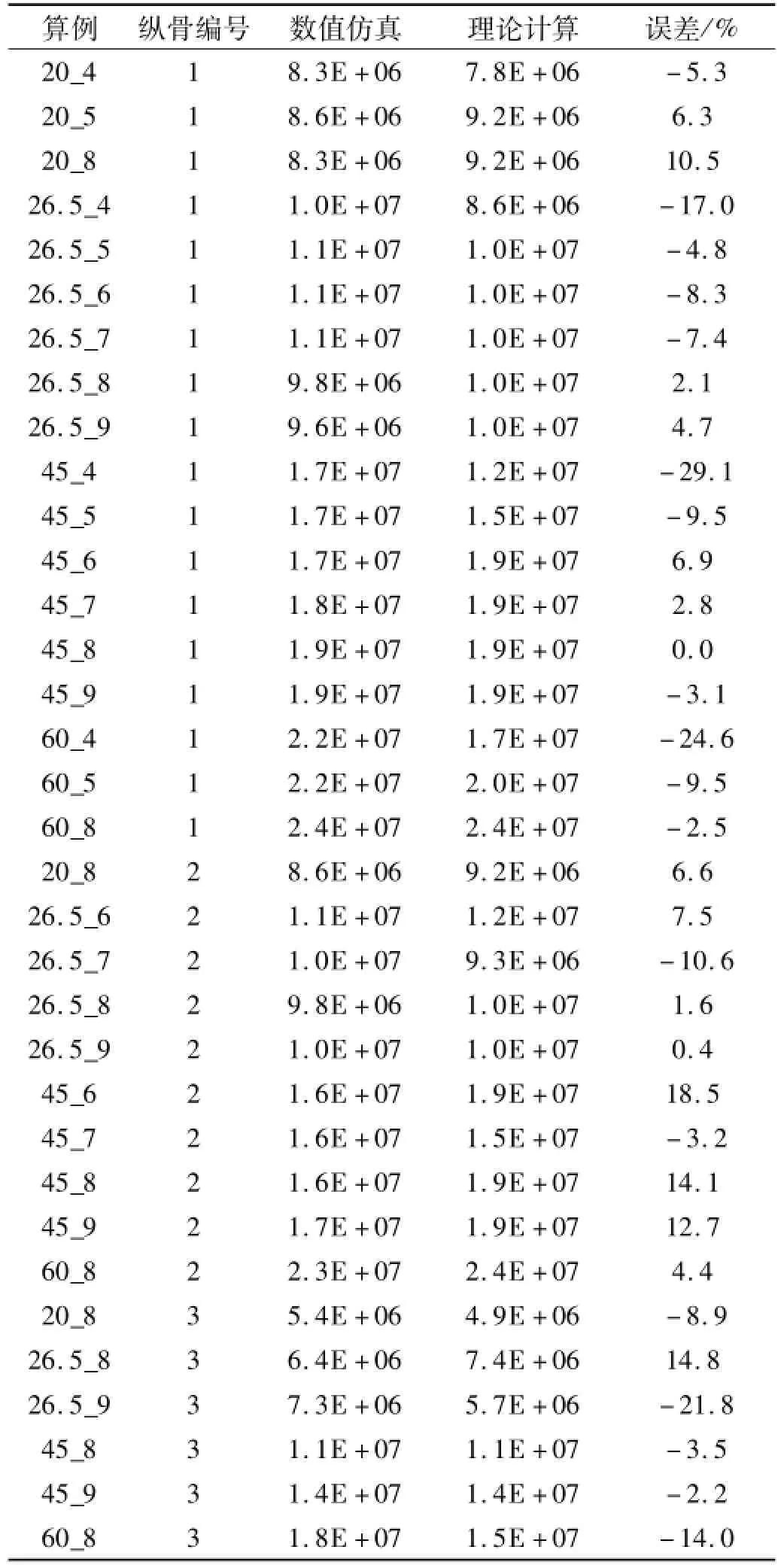
表6 完全变形骨材能量耗散的理论解的数值验证Tab.6 Theoreticalenergy dissipation of fully contacted and deformed stiffeners

图14 45＿5中1号骨材理论和数值能量随撞深变化曲线Fig.14 A comparison of numerical and theoretical energy versus crushing lengthfor stiffener No.1，Case 45＿5

由图14可见骨材的能量耗散随撞深变化基本上呈线性增加，新的理论模型和解析计算公式很好的捕捉到了这种趋势，二者吻合得较好。

6 结 论

本文主要研究船舶搁浅于台型礁石时双层底纵桁上骨材的变形和能量耗散机理。研究在分析现有的纵桁变形的理论模型的基础上，分析了现有模型的不足，并提出新的纵桁变形模型基于新纵桁变形理论模型并结合数值仿真技术计算结果，提出了纵桁骨材变形的理论模型。

礁石在双层底中滑移时，纵桁上骨材发生稳定的变形，能量耗散方式主要有三种：纵骨的弧形状变形的弯曲能量、纵骨的弧形状变形的膜拉伸能量和纵骨在垂向被礁石挤压弯曲的能量，其中，膜拉伸吸收能量最多。由于肋板与纵桁的交叉结构提升交叉处局部的强度和刚度，使得不同角度和撞深下的纵骨变性周期趋于相同，为肋板的间距。纵桁和其上的纵骨由于礁石挤压，局部形成倾斜的圆弧状的变形，使得在同一撞深下不同垂向位置的骨材完全变形后的变形的最大横向延伸距离基本相同。

应用塑性理论对纵骨变形模型进行分析，得到完全碰撞变形时的能量耗散和搁浅力。数值仿真结果显示同一位置处的纵骨在完全变形下数值随撞深变化趋于稳定，但对于不同位置的纵骨，同一撞深完全变形后的能量有差异。理论模型通过垂向周期理论很好的解释这种现象，理论解和数值结果吻合良好。

由于能量传递，未与礁石直接接触的纵骨会发生波及变形，其能量耗散模式仍保持线性，变形模态和周期与完全碰撞时保持一致，但变形的最大横向伸展逐渐减小，有关机理有待进一步研究。

［1］Hong L，Amdahl J.Plastic mechanism analysis of the resistance of ship longitudinal girders in grounding and collision［J］.Ships and Offshore Structures，2008，3（3）：159－171.

［2］Alsos H S，Amdahl，J.On the resistance of tanker bottom structures during stranding［J］.Marine Structure，2007，20（4）：218－237.

［3］Hong L，Amdahl J.Rapid assessment of ship grounding over large contact surfaces［C］.In：Proceeding of 5th InternationalConference on collision and grounding of ships；2010.June 14th－16th，Espoo，Finland，2010.

［4］Paik J K.On Qusai-Static crushing of a stiffened squared tube［J］.Journal of Ship Research，1996，40（3）：258－267.

［5］Hu ZQ，Amdahl J.A study on the effectofplate stiffeners of double bottom during ship grounding with large contact surface［C］.OMAE2011－49056 June，2011，Rotterdam，THE NETHERLANDS.

［6］刘 毅，王 晋，胡志强.船舶搁浅于台型礁石中的等效板厚法的研究［J］.工程力学，2013，30（8）：287－293.

LIU Yi，WANG Jin，HU Zhi-qiang.Investigation on smeared thicknessmethod for ship grounding over obstacles with large contact surfaces and trapezoidal cross section［J］，Engineering Mechanics，2013，30（8）：287－293.

［7］Amdahl J.Energy absorption in ship-platform impacts［PhDthesis］.［Trondheim（Norway）］：Department of Marine Technology，Norwegian University of Science and Technology，1983.

［8］Simonsen B C.Ship grounding on rock－I.Theory［J］.Marine Structures，1997（10）：519－562.

［9］Midtun，Amdahl J.Analysis of tankers during grounding and collision［Master thesis］.［Trondheim］：Department of Marine Technology，Norwegian University of Science and Technology，2006.

［10］Bo CerupSimonsen，Hanson Ocakli.Experiment and theory on deck and girder crushing［J］.Thin-Walled Structures，1999，34：195－216.

［11］Yu Z L，Hu Z Q.Plastic mechanism analysis of structural performances for stiffeners on outer bottom plate during shoal grounding accident［C］.ICCGS2013，June 17th－19 th，Trondheim Norway.

［12］Ohtsubo H，Wang G.An upper-bound solution to the problem of plate tearing［J］.Journal of Marine Science and Technology，1995，1：46－51.

［13］Hu Z Q，Amdahl J，Hong L.Verification of a simp lified analytical methodfor predictionsof ship groundings over large contact surfaces by numericalsimulations［J］.Marine Structures，2011，24：436－45.

Collapsemechanism of longitudinalweb girder attached stiffeners in a shoal grounding scenario of a double bottom tanker

YU Zhao-long1，HU Zhi-qiang1，2，WANGGe3，JIANG Zhe4
（1.State Key Lab of Ocean Engineering，Shanghai Jiaotong University，Shanghai200240，China；2.State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116023，China；3.American Bureau of Shipping，Singapore；4.CNOOC Research Institute，Beijing，China）

Plastic theory and numerical simulation were used to discuss deformation patterns and collapse mechanism of longitudinal web girder attached stiffeners in a shoal grounding scenario of a double bottom tanker.Numerical simulation code LS＿DYNA was used to calculate the deformation patterns and energy dissipation，and a mathematicalmodel of a progressively deforming stiffener was built.With the plastic theory，the deformation energy and themean grounding resistances were solved，and these results were verified with the numerical simulation method.The analytical calculation formulas obtained could be used to calculate and assess the crashworthiness of a ship during its design phase.

shoal grounding；longitudinal web girder attached stiffeners；analytical calculation；numerical simulation；deformation energy

U661.7

A

上海交通大学海洋工程国家重点实验室青年创新基金课题（GKZD010056－12）；ABSCOTC＆SJTU合作项目

2013－01－17 修改稿收到日期：2013－03－23

于兆龙男，硕士生，1989年生

胡志强男，副教授，1975年生