基于振动模态分析的钢轨中超声导波传播特性数值计算方法
何存富,刘青青,焦敬品,刘 飞,吴 斌
(北京工业大学机械工程与应用电子技术学院,北京 100124)
其中:级数中的每一项代表了一个在空间具有固定模式并按一定频率振动的驻波。可以看出,振动解利用
基于振动模态分析的钢轨中超声导波传播特性数值计算方法
何存富,刘青青,焦敬品,刘 飞,吴 斌
(北京工业大学机械工程与应用电子技术学院,北京 100124)
针对钢轨等复杂异型波导结构中超声导波频散特性难于求解的问题,通过振动模态分析提取出钢轨中超声导波传播特性。基于振动特征频率和波动解互相转化的原理,将振动模态分析获得的特征频率解,转换成波动解,进而提取出钢轨的频散特性。同时,还可以由结构振动分析中获得的变形信息,计算出超声导波的波结构。通过对计算出的钢轨中低阶超声导波模态频散特性和波结构分析,选择出适合钢轨无损检测的超声导波模态类型和频率范围,为后续专用超声导波传感器设计和检测实验提供理论支持。
模态分析;特征频率法;钢轨;超声导波;频散特性;波结构
高速铁路由于具有高速、大容量等优势,已经成为现代社会最重要的交通运输方式之一。随着我国高速铁路运营里程的跨越式发展以及客运高速化、货运重载化的发展,对高速铁路运输的安全性要求日益提高。特别是“7·23”动车追尾特大交通事故后,高速铁路运输的安全性更是备受人们关注。
作为高速铁路运输系统的重要组成部件,轨道具有引导机车前进、承受机车荷载以及将其传递至轨枕上的功能。由于自身材质缺陷以及长期受到各种外力及环境腐蚀综合作用,在轨道上会产生局部损伤甚至宏观断裂,从而导致列车出轨、倾覆等重大行车安全事故,造成人员伤亡和财产损失。因此,需要利用各种无损检测技术对钢轨的损伤状态进行检测。目前,常见的钢轨检测方法有超声波法、轨道电路、应变片检测法、光纤断轨检测法等。这些常规方法还不能满足现代轨道安全评价的需要,迫切需要发展高效、快捷的轨道无损检测新技术。作为一种新型无损检测技术,超声导波由于具有传播距离远、检测效率高等优点,对于钢轨大范围缺陷检测具有特殊优势,因此,钢轨超声导波检测技术也是目前国内外无损检测领域研究的热点问题。
由于超声导波的检测效果很大程度上取决于所选超声导波模态的传播特性。因此,对结构进行超声导波检测时,首先需要根据结构中超声导波的传播特性,如频散、波结构、衰减及可激励性,选择合适的超声导波模态类型和频率范围。对于规则截面波导(如板、杆、管)中超声导波的传播特性,其数值计算方法已经很成熟[1-5],且已有商用的数值分析软件[6]。但对于钢轨等异型截面波导中超声导波传播特性的研究,商用软件无法完成其分析计算。因此,异型截面波导中超声导波传播特性研究目前仍是超声导波研究领域的难点和热点问题。
国外很多学者[7-8]开展了异型截面波导中超声导波传播特性研究。例如,Rose等[9]利用半解析有限元的方法对任意截面波导中超声导波的传播问题进行了研究,计算出100 kHz频率范围钢轨中主要导波模态的相速度、群速度频散曲线,并在轨头踏面、轨头侧面进行了超声导波试验验证。同样采用半解析有限元方法,Lee等[10]采用半解析有限元的方法对钢轨中瑞利波及高频兰姆波传播特性进行了研究,并通过试验证明其对轨头下方的横向裂纹检测具有很好的敏感性。Coccia等[11]采用半解析有限元对不同激励条件下钢轨轨头中导波传播特性进行了研究,结果发现,对称激励时,能量主要集中在轨头踏面;非对称激励时,能量集中于轨头侧面。Hesse等[12]采用半解析有限元法对钢轨中表面波传播特性进行了理论分析。
综上所述,对于任意截面波导(包括钢轨)中超声导波传播特性的计算方法较单一,多采用半解析有限元计算频散特性,然后结合其他方法仿真或实验进行验证。针对以上研究现状,基于结构振动解与波动解的互化原理,本文利用振动模态分析的方法进行钢轨中超声导波传播特性的计算。
1 波动特性的振动求解原理
在给定扰动源及边界条件、初始条件下,弹性体的动力响应有波动解和振动解两种形式。介质中扰动质点间的弹性力逐渐传播的过程,称为弹性波。对于有界介质,由于扰动在其边界上来回反射,使得整个物体在其平衡位置附近呈现出一种周期性振荡现象,称为弹性体的振动。弹性波和弹性体的振动之间存在着本质的内在联系,可以看作是同一物理问题的不同表现形式。即扰动一开始总是以行波的方式将能量传播出去,而当物体有界时,由于行波的来回反射,最终使物体处于定常的运动状态,则表现为振动现象。弹性体的振动是波动过程的一种特殊形式。振动解可表示为无穷级数形式:无穷多个驻波的迭加描述了行波的传播,而驻波是由相同频率的简谐行波迭加得到。因此,通过傅里叶级数可以将波动解与振动解联系起来[13]。波动特性可以通过以下振动分析求解得到。
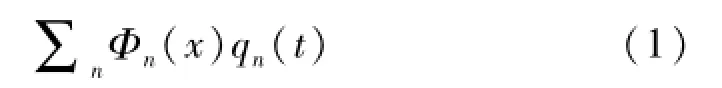
其中:级数中的每一项代表了一个在空间具有固定模式并按一定频率振动的驻波。可以看出,振动解利用
弹性体振动方程可以表示为:
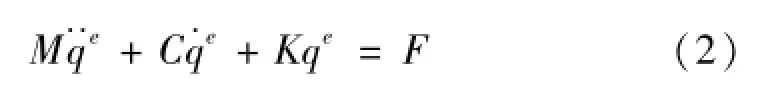
其中:M为质量,C为阻尼系数,K为弹性系数。
利用特征频率法对弹性体振动方程进行动力学求解,得到不同特征模态的振型Φ。通过对不同频率下不同特征模态的振型分析,可以计算出不同频率下该模式波的波数,从而得到该模式波的相速度

其中:cp为相速度,L为模型长度,k为波数。
进而求得其群速度

cg为群速度,Δf为频率差,Δk为波数差。
因此,利用振动解与波动解互化原理,通过对结构的振动模态分析,可以计算出任意截面波导的相速度及群速度频散特性,同时,还可以由结构振动分析中获得的变形信息,计算出超声导波的波结构。下面以钢轨异型截面波导为例,说明基于振动模态分析对任意截面波导中超声导波传播特性计算的有效性。
2 钢轨振动模态的有限元模型
基于COMSOLMultiphysics有限元软件平台,进行钢轨振动模态分析。参考GB 2585-2007标准[14],对60 kg/m钢轨进行有限元分析,轨底宽为150 mm,钢轨高度为176mm,轨头宽为73mm。由于结构的对称性,在计算钢轨中对称模态导波传播特性时,可以对其有限元分析模型进行简化,取钢轨的一半进行分析,模型如图1所示。其中,x方向为钢轨横截面的宽度方向,y方向为钢轨横截面的高度方向,z方向为钢轨长度方向。

图1 钢轨有限元分析模态Fig.1 Rail finite element analysismode
建立钢轨模型后,需要对其进行参数设置,主要包括材料属性、边界条件、网格划分、求解方式等。其中的材料性能参数设置主要包括:钢轨密度为7 824 kg/m3,杨氏模量为2.09×1011Pa,泊松系数0.29,热膨胀系数为1.21×10-51/K。有限元分析网格划分中设定的最大单元尺寸为0.000 3,网格单元层数为250层。求解方式选择特征频率求解,设定分析的特征频率范围为0~50 kHz。
3 结果分析
图2和图3给出50 kHz低频段范围内,几个典型模态的振型云图。从图2可以看出,随着频率的增大,振动从遍及整个截面逐渐过渡为集中在截面的局部区域,振动趋向复杂。
从图2(c)和图3中I~Ⅴ几种不同模态在46 kHz附近的振动云图可以看出,模态Ⅰ、Ⅱ、Ⅳ、Ⅴ振动主要集中在轨底部分,模态Ⅲ振动主要集中于轨头部分,且模态振动幅度有差别。

图2 模态Ⅰ振型图Fig.2 Shapes ofmodalⅠ

图3 模态振型图Fig.3 Modal shapes
3.1 频散特性
在模态分析基础上,根据不同频率下不同特征模态的振型,计算出不同频率下该模式波的波数。图4给出通过模态分析获得50 kHz频率范围内对称模态导波的波数-频散曲线。
根据式(2)及式(3),可进一步计算得到50 kHz频率范围内钢轨的相速度及群速度频散曲线,结果如图5和图6所示。
可以看出,随着频率的增加,钢轨中超声导波模态的数量急剧增加,且不同模态的导波均存在频散现象。因此,在进行钢轨超声导波检测参数选择时,需要考虑超声导波的这些传播特性,通过探头设计及检测参数优化避免多模态激励,并避开频散严重的检测频带。
为清晰反映图2~3中五种模态导波的频散特性,图7给出该五种模态导波的群速度频散曲线。其中,模态Ⅰ为粉色圆点曲线,模态Ⅱ为天蓝色圆点曲线,模态Ⅲ为红色圆点曲线,模态Ⅳ为绿色圆点曲线,模态Ⅴ为蓝色圆点曲线。

图4 钢轨中超声导波的波数频散曲线Fig.4 Wavenumber dispersion curves of ultrasonic guided wave in rail

图5 钢轨相速度频散曲线Fig.5 Phase velocity dispersion curves of rail

图6 钢轨群速度频散曲线Fig6.Group dispersion curves in rail
3.2 波结构
根据不同频率下各模态的位移分析,可以得到不同频率下各模态导波的波结构。图8~图12给出46 kHz附近Ⅰ~Ⅴ五种模态导波的波结构。对比可以发现,模态Ⅰ、Ⅱ、Ⅳ、Ⅴ的位移主要集中在轨底部位,而模态Ⅲ的位移集中在轨头部位。对比模态Ⅰ、Ⅱ、Ⅳ、Ⅴ沿不同方向位移分布可知,在轨底部位,模态Ⅳ沿导波传播方向位移较大,且在轨底部分分布较均匀,因此,该频率的模态Ⅳ在轨底中传播能力强,对整个轨底部分的缺陷具有较高灵敏度,适合轨底无损检测使用。
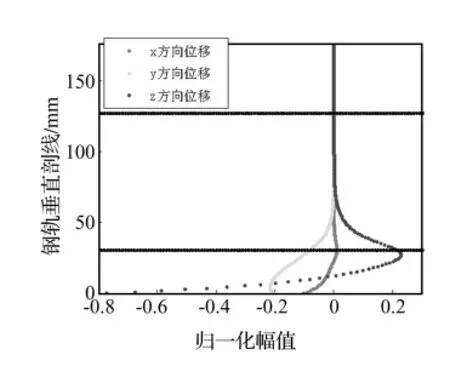
图8 在46.4 kHz处模态Ⅰ的波结构Fig.8Wave structure of modalⅠat 46.4 kHz
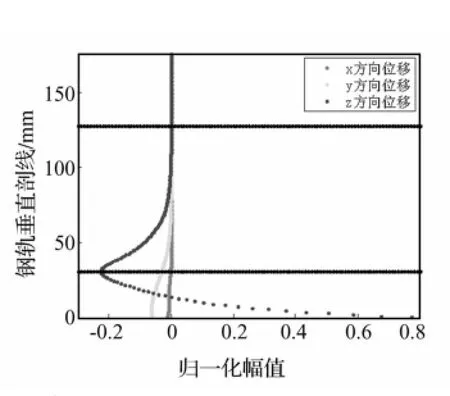
图9 模态Ⅱ在46.6 kHz时的波结构Fig.9 Wave structure of modalⅡat 46.6 kHz

图10 模态Ⅲ在46.3 kHz时的波结构Fig.10 Wave structure of modalⅢat46.3 kHz

图11 模态Ⅳ在46.2 kHz时的波结构Fig.11 Wave structure of modalⅣat46.2 kHz
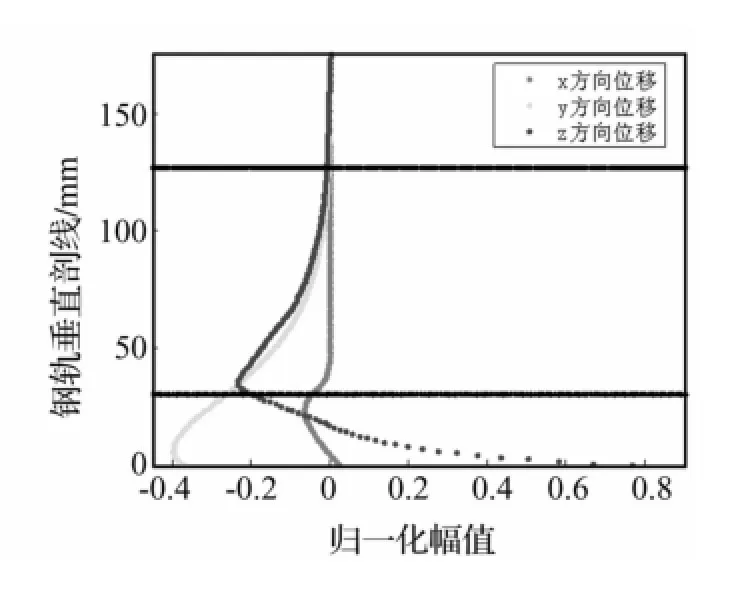
图12 模态Ⅴ在46.5 kHz时的波结构Fig.12 Wave structure of modalⅤat46.5 kHz
4 结 论
利用振动模态分析法,本文实现钢轨异型截面波导中超声导波频散和波结构等波动特性计算。并在低频50 kHz范围内,对五种典型模态导波的频散特性和波结构进行了对比分析。研究发现,在46 kHz附近,各模态导波频散相对较小,且Ⅰ、Ⅱ、Ⅳ、Ⅴ模态位移主要集中在轨底,而其中的中模态Ⅳ在轨底中传播能力最强,且在轨底部位具有较均匀的位移分布,适合于轨底部位的无损检测。模态Ⅲ的位移集中在轨头部位,适合于轨头部位的无损检测。后续将基于理论分析结果,利用选定的导波模态类型和频率范围,开展轨底和轨头部位的无损检测实验研究。
[1]郑祥明,赵玉珍,史耀武.兰姆波频散曲线的计算[J].无损检测,2003,25(2):66-68.
ZHENG Xiang-ming,ZHAO Yu-zhen,SHI Yao-wu.Calculation for Lamb wave dispersion curves[J].NDT,2003,25(2):66-68.
[2]刘增华,何存富,吴 斌.单层板频散曲线的矩阵表示及Matlab实现[J].无损检测,2005,27(5):225-227.
LIU Zeng-hua,HE Cun-fu,WU Bin.Matrix expression for dispersion curve of single plate and its implementation by Matlab[J].NDT,2005,27(5):225-227.
[3]阎 石,张海凤,蒙彦宇.Lamb波频散曲线的数值计算及试验验证[J].华中科技大学学报(城市科学版),2010,27(1):1-4.
YAN Shi,ZHANG Hai-feng,MENG Yan-yu.Numerical calculation and experimental validation for Lamb wave dispersion curves[J].J.of HUST,(Urban Science Edition)2010,27(1):1-4.
[4]何存富,李隆涛,吴 斌.超声导波在管道中传播的数值模拟[J].北京工业大学学报,2004,30(2):129-133.
HE Cun-fu,LI Long-tao,WU Bin.Numerical simulation of guided ultrasonic wave transmitted in pipe[J].Journal of Beijing University of Technology,2004,30(2):129-133.
[5]何存富,李隆涛,吴 斌.空心圆柱体中的周向超声导波[J].机械工程学报,2004,40(8):7-12.
HE Cun-fu,LI Long-tao,WU Bin.Guided circum ferential waves in hollow cylinders[J].Chinese Journal ofMechanical Engineering,2004,40(8):7-12.
[6]Lowe M.Matrix techniques formodeling ultrasonic waves in multilayeredmedia[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1995,42(4):525-542.
[7]Bray D E,Egle D M.Rayleigh wave dispersion in the coldworked layer of used railroad rail[J].Journal of the Acoustical Society of America,1987,64(3):845-851.
[8]Hirao M,Kyukawa M,Sotani Y,et al.Rayleigh wave propagation in a solid with a cold-worked surface layer[J].Journal of Nondestructive Evaluation,1981,2(1):43-49.
[9]Hayashi T,Song W J,Rose J L.Guided wave dispersion curves for a barwith an arbitrary cross-section,a rod and rail example[J].Ultrasonices,2003,41(3):175-183.
[10]lee CM,Rose JL,Cho Y.A guided wave approach to defect detection under shelling in rail[J].NDT&E International,2009,42(3):174-180.
[11]Coccia S,Bartoli I,Marzani A,et al.Numerical and experimental study of guided waves for detection of defects in the rail head[J].NDT&E International,2011,44(1):93-100.
[12]Hesse D,Cawley P.Surfacewavemodes in rails[J].Journal of the Acoustical Society of America,2006,120(2):733-740.
[13]杨桂通,张善元.弹性动力学[M].北京:中国铁道出版社,1988:1-15.
[14]GB 2585-2007.铁路用热轧钢轨[S].中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会,2008.
Propagation characteristics of ultrasonic guided wave in rails based on vibration modal analysis
HE Cun-fu,LIU Qing-qing,JIAO Jing-pin,LIU Fei,WU Bin
(College of Mechanical Engineering and Applied Electronic Technology,Beijing University of Technology,Beijing 100124,China)
Aiming at difficult problems to solve the dispersion characteristics of ultrasonic guided wave in complex waveguide structures,such as,rails,here the vibration modal analysis method was used to extract the propagation characteristics of ultrasonic guided wave.Based on the principle that vibration characteristic frequencies and wave solutions can convert each other,the solutions of characteristic frequencies obtained with vibration modal analysis were converted into wave solutions,and then the dispersion characteristics of railswere extracted.Deformation information was gained from vibration analysis of a structure,and with it the wave structure of ultrasonic guided wave was calculated.The dispersion information and wave structure information of lower ordermodes of ultrasonic guided wave were analyzed,the modal type of ultrasonic guided wave and its frequency range were selected,all of them provided a theoretical support for designing special ultrasonic guided wave sensors andmeasuring tests.
modal analysis;method of characteristic frequencies;rail;ultrasonic guided wave;dispersion characteristics;wave structure
TB553
A
国家自然科学基金项目(51235001,11272017);北京市自然科学基金项目(1122005)
2012-12-12 修改稿收到日期:2013-03-19
何存富男,博士,教授,1958年7月生

