电磁轨道炮发射过程的轨道变形研究

雷 彬，李 鹤，李 军，李治源，朱仁贵

电磁轨道炮发射过程的轨道变形研究

雷 彬1，李 鹤1，李 军2，李治源1，朱仁贵1

电磁轨道炮是一种利用电磁能驱动电枢滑动至超高速的新概念动能武器，具有初速高、射程远、可控性强、低发射特征等优点，在未来军事领域具有广阔的应用前景［1］。电磁轨道炮在发射过程中，轨道副上由于流过反向的脉冲大电流，会产生相互排斥的作用力。随着电枢的不断向前滑动，轨道上会产生类似梁的横向挠度变形。典型轨道炮结构包括轨道、绝缘支撑体和紧固部件，轨道变形会引发紧邻部件的相应变形，降低支撑强度，缩短轨道炮寿命。

对于移动载荷引发的轨道变形，学者们［2－3］大都将轨道简化为弹性基底上的悬臂梁或简支梁模型来求解其动力学响应。对于这一类问题，解析求解过程已经比较成熟，解析方法也多种多样［4－6］。在试验测量方面，Johnson等［7］利用光纤布拉格光栅应力传感器（fiber Bragg grating strain sensors）测量了轨道发射时的动态应变，发现电枢的临界速度值低于伯努利－欧拉梁理论模型的预测估算值，并提出求解结构动力响应，必须考虑电枢的磨损，因而求解的关键在于确定移动载荷的精确值。

本文将在轨道通用动力学方程的基础上，根据实际发射时的电流数据，确定电枢速度和位移的变化，考虑电枢的磨损，求解精确的动力响应值，并对比由此带来的差异大小。

1 弹性梁模型与移动载荷

轨道的两端自由弹性基础梁模型如图1所示，轨道上受力包括电枢对其施加的作用力Fa（t）和另一侧轨道的斥力，其集度用q（t）表示。

对于两端自由的弹性梁，移动载荷下轨道横向变形ω（x，t）的通用动力学控制方程就可以写为：

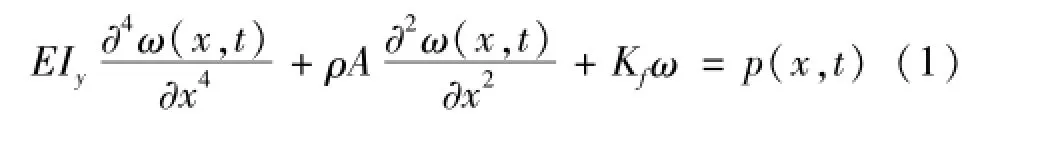
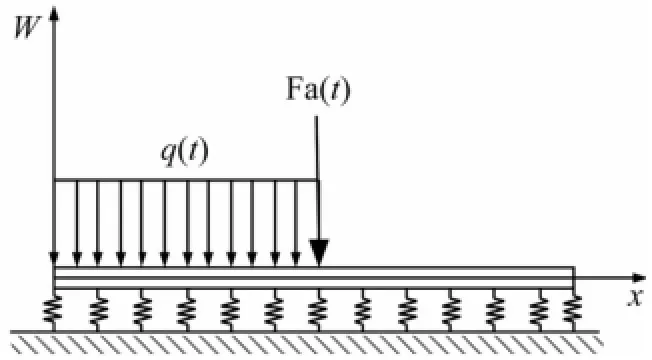
图1 轨道的弹性基础梁模型ig.1 Elastic foundation beam model of rail

其中：E为轨道材料的杨氏模量，Iy是轨道横截面惯性矩，，这里，b为轨道宽度，h为轨道厚度；Kf是弹性基础的弹性系数；A是轨道的横截面面积；对于矩形截面轨道A＝hb；ρ代表轨道材料密度，p（x，t）是轨道上施加的载荷，t代表时间。

对式（1）进行傅里叶和拉普拉斯系列变换后，可以将关于轨道位置和时间的挠度曲线表示为［8］：

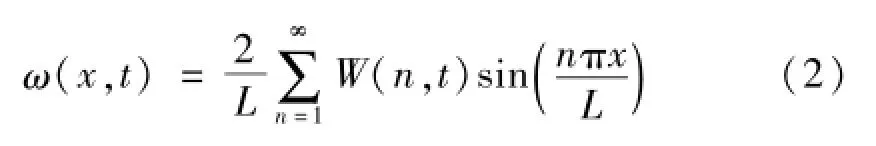
式中：L是轨道的长度，n为半波数。

其中：l（t）是电枢距离起始位置的距离，δ［x－l（t）］和H［x－l（t）］分别是Dirac函数和Heaviside函数。电枢侧翼在滑动中不断磨损，设电枢的磨损系数为常数k，则k可以定义为，其中l′是电枢的有效磨损距离。电枢对轨道的实际作用力也随着时间不断减小，可以表示为：

Fa（t）＝Fa（1＋k）（8）

轨道上的斥力集度可以表示为［8］：

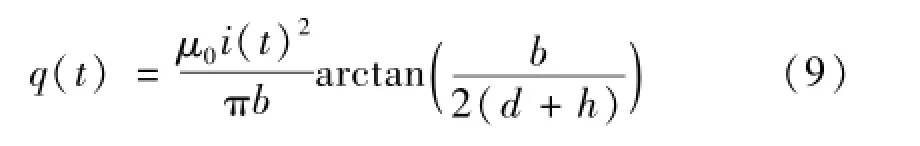
其中：μ0是真空磁导率；i是脉冲电流值；d是轨道间距。

2 电枢运动参量计算

对于轨道的挠度变形计算，采用的轨道发射系统参数为L＝6 m，b＝0.04 m，h＝0.01 m，d＝0.03 m，ρ＝8 300 kg／m3，Kf＝5.5×109N／m，E＝114 GPa。枢轨间不发生烧蚀的情况下，电枢对轨道的作用力可以按照“每安培一克”的经验法则近似表达理想的接触压力［9］，设Fa＝3 000 N，l′＝L。图2是实际发射试验中，用示波器采集到的电流数据拟合波形，电枢在轨道中滑动4.5 ms后出膛。从图中可以看出，发射过程持续4.5 ms，电流的峰值约300 kA，平台区间约2.5 ms。

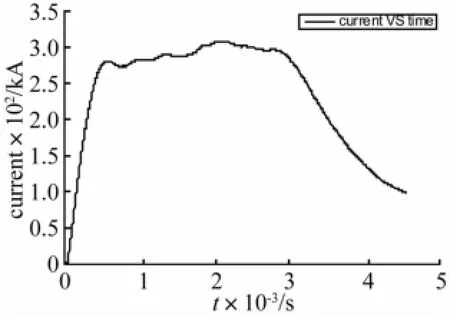
图2 发射过程轨道电流波形Fig.2 Breech current during electromagnetic launch

电枢的运动速度依赖于电流产生的推力，可以描述为：

其中：L′是轨道的电感梯度，m为电枢质量。电枢在轨道上滑动距离随时间的关系可以写为：

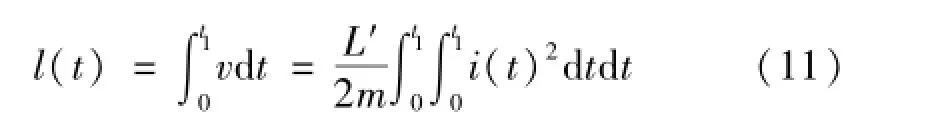
图3中黑实线和虚线分别是电枢的运动速度和滑动距离，可以看出，拟合计算的速度数值比实际测量值（图中的点）高一些，这是因为在计算的过程中，没有考虑电枢的摩擦和空气阻力等带来的影响。由于发射过程只有ms量级，数据采集处理过程中标定的时间会出现一定的误差，而且电流波形的测量和用Matlab进行的曲线拟合（图2）也都存在一定的取舍。因此，图3中标记的测量值点都在拟合曲线上下浮动。但是，拟合值与试验测量值所表述的电枢速度和位移变化趋势一致，因此，拟合曲线可以用于下一步的计算。

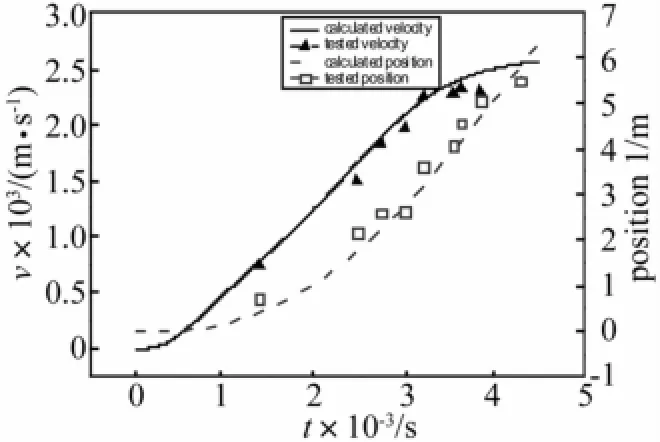
图3 发射过程电枢速度和位置随时间的变化Fig.3 Armature velocity and position profile VS time

3 计算结果及分析

将图3所示的电枢速度、滑动距离和第二节中的轨道结构和材料参数等数值代入第一节的公式，采用MATLAB编写计算程序，对轨道的变形进行数值计算，可以求得轨道上各点随时间和滑动距离的变化情况如图4所示。从图中可以看出，轨道上接近炮尾部分的变形要大于接近炮口部分的，且轨道上的变形出现一定的震荡。更详细直接的观察还需要借助二维图示。

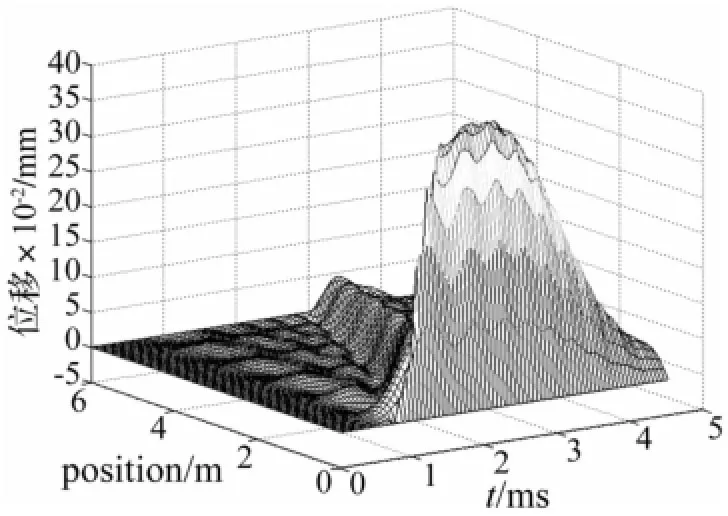
图4 轨道振动随时间的和滑动距离的三维图Fig.4 Rail deformation along with sliding distance and launch time

为了对比分析接触压力及电枢磨损对轨道变形带来的影响，分别计算了有电枢的接触压力和磨损情况下，轨道中点（x＝3 m）处，变形随时间的变化，其结果如图5所示。为了便于区分，对曲线进行符号标记，由于计算步长太短，所以对数据间隔采样来标记。可以看出，当考虑电枢的接触压力后，变形幅值要高于轨道单独斥力作用下产生的幅值；有磨损系数时，接触压力产生的变形要小于无磨损情况下的，而这是较准确地反映轨道变形的曲线。在2 ms之前，轨道中点受到移动载荷的作用很小，变形幅值也很小。在此之后，电枢的压力首先对轨道中点产生作用，产生一个小幅值的振荡。结合图3，可以看到在3.1 ms左右，电枢到达轨道中点，电枢压力和轨道斥力共同作用，在轨道上产生一个较大幅值的变形。在发射结束时刻，由于磨损增加，电枢压力逐步减小，因此曲线逐渐向一起靠拢。相对于轨道斥力单独作用，考虑电枢压力后，轨道中点的变形峰值约提高67%。当计入电枢的磨损后，其变形峰值提高约30%。

考虑电枢的初始预应力和磨损带来的作用力变化应该是更贴近实际的振动情况，在此作用力下，对不同时刻和不同位置时的振动情况进行了计算如图6和图7所示。

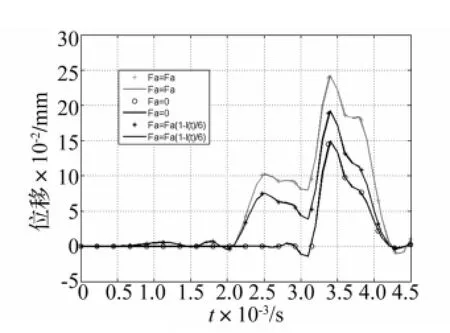
图5 不同载荷下轨道中点变形变化Fig 5 Deformation of rail center point under different loads

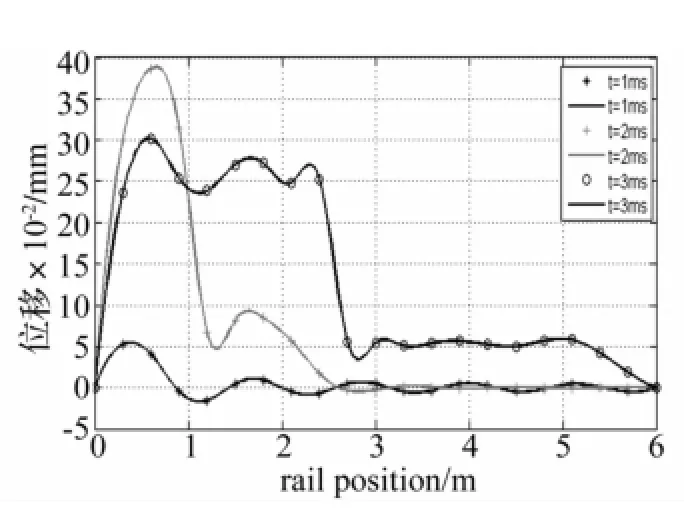
图6 不同发射时刻的轨道变形Fig 6 Deformation of rail under different launch time

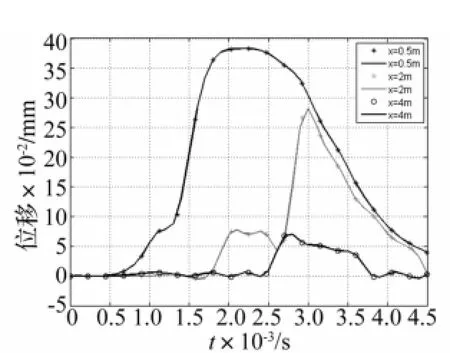
图7 不同位置处轨道随时间的变形Fig 7 Rail deformation along with time under different position

图6所示是不同时刻，轨道各点的变形变化。在t＝1 ms时刻，电枢大约在1 m的位置，速度很低，从炮尾至炮口，轨道出现幅度很小的衰减正弦波，第一个波长约1.5 m。在t＝2ms时刻，受电枢压力和轨道斥力作用，距离炮尾1m的轨道中出现了很大幅度的变形，在1.5m以后变形幅值明显减小。在3 ms时刻，距离炮尾1m内的轨道振幅下降，但是中等幅值的变形延续至轨道的3 m处。这是由于在电枢滑动的2 ms以前，轨道受到瞬间的冲击力比较大，所以变形较大。在3ms时，随着电枢的向前滑动，轨道中的动力波也向前传播，出现图6中黑圈线前半部分所示的波动。结合图2和图3可以看出，轨道响应幅值的大小跟电枢在轨道上的位置和流过相应轨道的电流强度密切相关。电枢滑动到3m以后，电流开始衰减，轨道间相互斥力的分布载荷q也相应减小，因此，前段轨道受到响应的幅值和持续时间均要高于后段轨道的。

图7所示是不同位置处，轨道各点随时间的变形情况，0.5m处的变形贯穿整个发射过程，其变形波形类似于正弦波的前半个周期，在大约2ms时达到最大值，在2.5 ms后开始衰减。这是因为此处轨道在整个发射过程中，一直承受电流产生的轨道斥力作用，轨道向外变形过程又受到绝缘支撑体的约束，在2～2.5ms区间达到近似平衡；随后，随着电流波形开始衰减，但是振动的衰减比电流提前，这一方面是由于此处动力波的传播不断卸载能量，另一方面是计算中的近似取值和计算误差造成的。2m和4m处发生明显变形的时刻相应地都向后延迟了，而且位置越靠近炮口其变形幅值越小。在发射结束时刻，各个点的变形都接近0 mm，轨道斥力和电枢压力突然消失，轨道各点开始自由变形并逐渐衰减至零。在这里可以明显地看到轨道的变形严重依赖于电枢的运动位置和电流波形的变化。炮尾部分轨道的变形要大于炮口部分轨道，这是因为一方面，炮尾部分受到电流作用时间更长，另一方面，3 ms后，电流开始衰减，后段轨道受到的斥力载荷要小一些。

综合上述计算结果，可以看出轨道炮发射过程中，轨道的变形幅值呈现一定的震荡。在重复或者连续发射时，这种变形也可能会对轨道炮发射结构和寿命产生严重的影响。

4 结 论

（1）轨道中点的变形研究表明：不同压力条件下，轨道上的变形是不同的，为了获得更为精确的变形值，需要考虑电枢压力和电枢的磨损。

（2）电枢滑动到某一位置时，在轨道斥力和电枢压力作用下，电枢滑过区域的轨道变形要远大于电枢未到达的区域。

（3）在发射过程中，轨道上最大的变形峰值出现在炮尾一段，而且轨道位置越接近炮口，变形峰值越小。因此，电磁轨道炮发射过程中，需要对炮体结构的尾部支撑体进行重点加强。

［1］吕庆敖，雷 彬，李治源，等.电磁轨道炮军事应用综述［J］.火炮发射与控制学报，2009（1）：92－96.

LÜQing-ao，LEI Bin，LI Zhi-yuan，et.al.Summary of Electromagnetic Railgun Military Application.［J］.Joutnal of Gun Launch＆Control，2009（1）：92－96.

［2］Tzeng T，Sun W.Dynamic response of cantilevered rail guns attributed to projectile／gun interaction-theory［J］.IEEE Transactions on Mabnetics，2007，43（1）：207－213.

［3］刘郑国，田福庆.电磁轨道发射装置结构动力学特性分析［J］.船舶力学，2010，14（10）：1158－1164.

LIU Zheng-guo，TIAN Fu-qing.Structure dynamic characteristic analysis of electromagnetic rail launcher［J］.Journal of Ship Mechanics，2010，14（10）：1158－1164.

［4］刘 文，李 敏，白象忠，等.电磁炮发射轨道受指数函数磁压力的变形计算［J］.哈尔滨工业大学学报，2010，42（8）：1336－1340.

LIU Wen，LI Min，BAI Xiang-zhong，et.al.Deformation calculation of electromagnetic Launcher＇s rail subjected to exponentialmagnetic pressure［J］.Joutnal of Harbin Institute of Technology，2010，42（8）：1336－1340.

［5］陈铁宁，白春艳，张益男，等.电枢运动引起电磁发射轨道的动态响应［J］.动力学与控制学报，2010，8（4）：360－364.

CHEN Tie-ning，BAI Chun-yan，ZHANG Yi-nan，et.al.Dynamic respnse of electrmagnetic railgundue to armature movement［J］.Joutnal of Dynamics and Control，2010，8（4）：360－364.

［6］田振国，白象忠，杨 阳.电磁轨道发射状态下导轨的动态响应［J］.振动与冲击，2012，31（2）：10－14.

TIAN Zhen-guo，BAI Xiang-zhong，YANG Yang.Dynamic response of rail under a launching state of an electromagnetic rail［J］.Joutnal of Vibration and Shock，2012，31（2）：10－14.

［7］Johnson A J，Haran T，Moon F C，et al.Stress wave measurements in an electromagnetic launcher［C］.2008 14th Symposium on Electromagnetic Launch Technology 2008：1－6.

［8］Daneshjoo K，Rahimzadeh M，Ahmadi R，et.al.Dynamic response and armature critical velocity studies in an electromagnetic railgun［J］.IEEE Transactions on Magnetics，2007，43（1）：126－131.

［9］Marshll R A，Wang Y.Railguns：their science and technology［M］.Beijing：China Machine Press，2004.

（1.军械工程学院弹药工程系，石家庄050003；2.北京特种机电研究所，北京 100012）

电磁轨道炮发射电枢过程中，移动载荷对轨道的作用会引发轨道挠度变形。依据试验电流波形数据确定电枢速度和滑动距离，根据弹性梁的动力学响应方程，考虑电枢的作用力及磨损，求解了轨道的挠度幅值。对比了电枢作用力和轨道斥力对轨道变形幅值的影响，获得了轨道的挠度变化随轨道位置和发射时间的变化曲线，为进一步分析轨道炮寿命和绝缘支撑体结构设计提供参考依据。

电磁轨道炮；轨道变形；移动载荷；接触压力

Rail deformation during launching of an electrom agnetic railgun

LEIBin1，LIHe1，LIJun2，LIZhi-yuan1，ZHU Ren-gui1
（1.Department of Ammunition Engineering，Ordnance Engineering College，Shijiazhuang 050003，China；2.Beijing Institute of Special Electromechanical Technology，Beijing 100012，China）

In the launching armature of an electromagnetic（EM）railgun，themoving loads due to the armature's sliding can cause the rail's dynamic response.Here，based on the basic theory of an elastic beam，amodelwas developed to investigate the rail's dynamic response.According to the armature velocity and its sliding distance determined with current data obtained from launching tests，the rail deflection curre under moving loads was gained.The deformations of the rail with varying of rail position and launching time were obtained，and the effects of rail repulsion and armature contact force on the rail's deformationswere compared.These results provided a reference for further design of supporting structures and further analysis of EMrailgun life length.

EMrailgun；rail deformation；moving loads；contact pressure

TJ399

A

十二五军队预先研究项目

2012－12－12 修改稿收到日期：2013－03－11

雷 彬男，博士，教授，博士生导师，1962年9月生