Mecanum万向轮滚子外轮廓曲面变形补偿设计

张学玲，侍才洪，康少华，胡军中

（1.军事交通学院，天津 300161；2.浙江美科斯叉车有限公司，浙江 杭州 311400）

对于需要自由运动或精确定位的设备，如大型设备拆卸，安装及检修升降机、机器人、叉车等，安装Mecanum万向轮，可以通过对4个万向轮旋转方向的控制，实现车辆在2D平面内的任意运动，即纵向、横向与旋转3个自由度的运动.Mecanum万向轮的结构大致相似，多数文献对其运动的控制进行了研究［1－3］.但由于 Mecanum万向轮结构较复杂，按照传统理论计算设计的结构，运行中由于受工作载荷作用会变形，使得行走过程发生振动，运动平稳性难以保证，进而影响车辆的运行可靠性.本文针对这个问题，研究运行中载荷对滚子变形的影响，对滚子廓线进行变形补偿，使外廓设计更精确合理.

1 Mecanum万向轮结构设计

1.1 Mecanum万向轮整体结构设计

Mecanum万向轮为复合结构，如图1a所示.主体部分为主动旋转的中心车轮骨架，围绕外缘均布安装若干自由随动滚子，其轴线与主体骨架垂直于轴线的中心平面成45°角.这种结构使滚子滚动时可以产生沿着轮体中心轴线和垂直于轴线的力，实现万向运动的功能.为保证运行时的平稳，Mecanum万向轮的布置方式在前视基准面的投影为圆，如图1b所示，右视基准面的投影为近似矩形，如图1c所示.

由于运行中滚子受载变形，会使其在前视基准面的投影不为圆，尤其在两个滚子交替接地过程中，会出现较大的振动现象.为增大滚子与地面的摩擦系数，在滚子外壳压制有橡胶层.由于橡胶材料的弹性大，受力更易产生变形，因此，需要对滚子进行变形补偿，使其在负载运行时尽量保持圆柱形状.

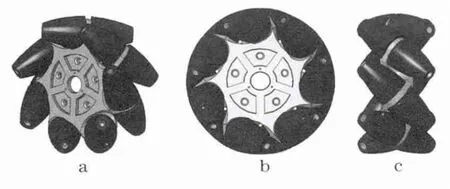
图1 Mecanum轮的结构Fig.1 Structure of mecanum wheel

1.2 Mecanum万向轮滚子廓线设计

正确设计滚子的轮廓曲线，使轮体在前视基准面的投影为圆，这是Mecanum万向轮精度的基础.由于轮体外廓的包络线为圆柱，则滚子的母线可视为绕主体骨架轴线的螺旋线［4］.若Mecanum轮的半径为R，滚子半径为r，滚子长度为Lr，滚子轴与主体骨架垂直于轴线的中心平面角度为γ，则滚子的轮廓面母线为半径R的圆柱体与成γ角度的平面的交线中的一段，如图2所示.图2中，φ为滚子在前视投影面对应的角度，lw为Mecanum轮厚度.

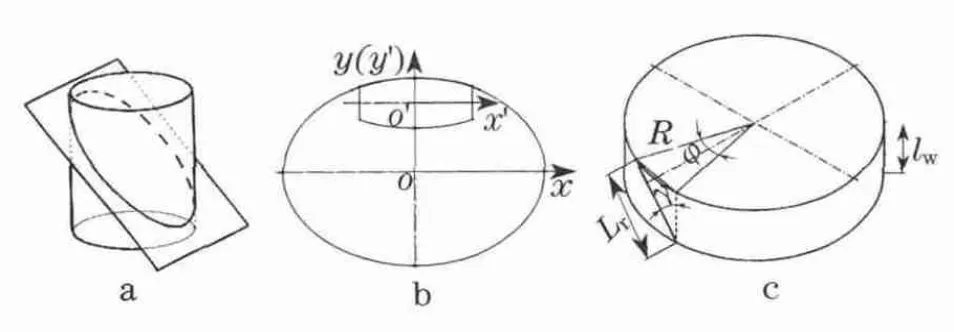
图2 滚子母线轮廓曲线Fig.2 Outline curve of roller generatrix

如图2a所示，在坐标系xO′y内，椭圆曲线即滚子的母线方程可写为

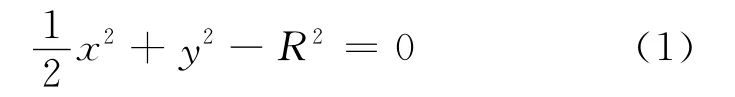
以滚子中心为坐标原点，即在坐标系xO′y内，如图2b所示，该滚子的母线方程可写为

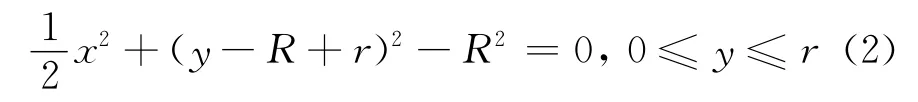
设Mecanum轮共有n个滚子组成，φ＝2π／n，如图2c所示.为使投影圆连续，滚子需要足够长度，则滚子的最小长度Lrmin为

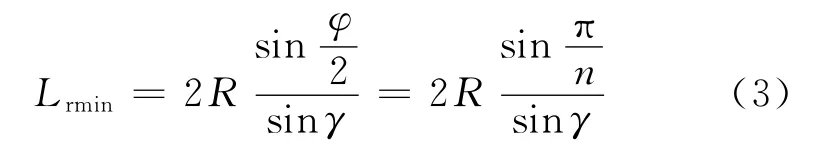
为保证行走平稳，需使轮体各滚子间的重合度大于1，一般取滚子长度Lr范围为：Lrmin≤Lr＜重合度ε表示为

则相邻滚子在末端同时与地面接触的长度l为

根据式（2）可以计算出滚子的外轮廓母线的坐标值.然后根据滚子长度Lr在曲线上截取滚子所在区段，即设计的滚子外轮廓曲线.按照滚子的支撑固定位置，万向轮结构分为中间支撑与两端支撑两种.两端支撑的滚子可以采用整体滚子，中间支撑的滚子则必须采用二分式滚子，从中间分开并留出安装空间.本文采用滚子中间支撑结构，滚子外廓母线曲线数据如表1中的第2，3列（理论廓线x坐标，理论廓线y坐标）所示，该数据可用于滚子的设计和加工.以此数据设计的滚子如图3所示.

图3 滚子理论计算廓线Fig.3 Theoretic contour of roller

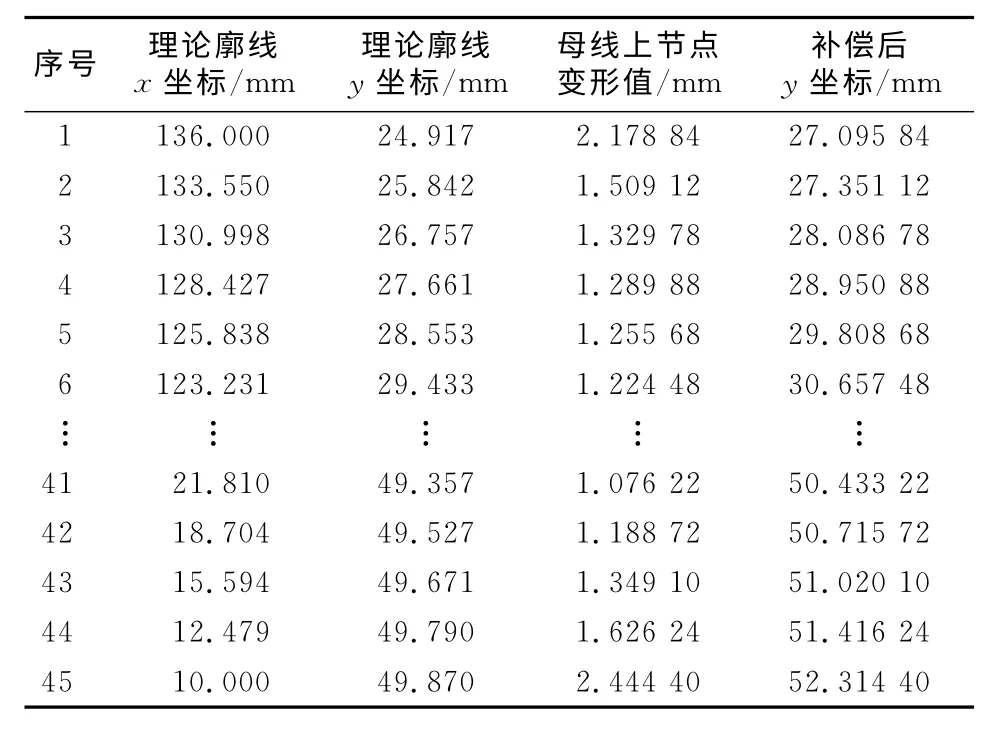
表1 滚子廓线坐标值Tab.1 Partialcoordinates of roller profile

2 Mecanum万向轮滚子轮廓补偿

滚子外壳采用橡胶材料，与钢内核套接.车辆行走时滚子受到地面压力和摩擦力的作用，橡胶外壳产生变形，引起运行不平稳或振动，因此，需要对滚子外壳轮廓进行变形补偿［5－7］.

2.1 滚子外壳受载荷变形仿真计算

以滚子橡胶外壳为对象，基于有限元方法对其进行非线性变形仿真计算.由于模型对称，建立一半几何模型.采用SOLID185单元，材料为各向同性的高弹性橡胶材料，弹性模量为6 900MPa，泊松比为0.49.参数C01和C10根据材料试验求取.边界条件为：在胶外壳与钢内核接触面加约束，与地面接触部分加载荷，即沿滚子母线方向分段依次加载.载荷值大小为车辆满载时，单个Mecanum轮受到的重力以及地面摩擦力，载荷方向为径向的重力和切向的摩擦力［8］.图4所示为有限元模型及边界条件.经非线性计算，可得到一系列滚子的不同位置与地面接触时局部受载的变形结果，如图5所示.从变形值可以看出，滚子两端的变形量较大，为中部变形量的2倍左右.

图4 滚子橡胶外壳模型及边界条件Fig.4 Finite element model and boundary condition of rubber roller cover

图5 滚子不同位置与地面接触时的变形结果Fig.5 Displacement contours while roller contact ground with different position

把分段载荷同时加载，可以视为单个滚子滚过地面这一段时间段内，滚子外壳变形量的整体效果.这时得到滚子外壳整体变形图，如图6所示.变形与分段加载时结果近似.

橡胶材料受挤压变形小于受拉和剪切，在滚子中部局部受载时，由于四周材料的挤压，变形量不大，而在两端，材料在压力作用下向两侧移动，使得变形量较大.

3.2 滚子外廓补偿

在滚子外壳变形量较大的地方适当加厚材料，可以补偿滚子受载造成的变形.在滚子的理论外轮廓母线曲线上叠加上变形量曲线即为补偿后的滚子外轮廓母线.为便于叠加，要使理论轮廓坐标计算点与变形仿真节点一一对应，为此可以使用插值方法.本文采用理论轮廓母线分段步长与仿真模型的母线分段步长一致的方法.根据仿真计算结果，提取滚子外壳外表面母线上各节点的变形值（母线上的节点即图4中的网格节点），如表1中第4列（母线上的节点变形值）所示.变形曲线如图7所示.

图6 滚子外壳整体变形图Fig.6 Deformation contour of roller cover

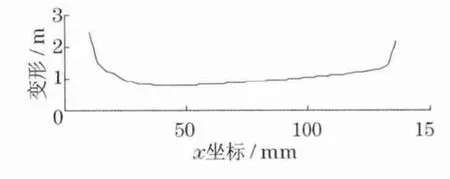
图7 滚子外壳变形值随x坐标曲线Fig.7 Deformation curve of roller cover to x axis

图7所示曲线可以作为滚子橡胶外壳母线的变形补偿理论曲线.表1中第3列与第4列叠加即为补偿后的滚子轮廓母线.但考虑到实际情况，要对补偿值作下述修正处理：①由于滚子重合度大于1，滚子末端接触地面同时，有2对滚子与地面接触受力.本文设计的Mecanum轮滚子重合度为1.27，为使相邻滚子接地过渡平稳，避免滚子交替时引起振动，在轴向截面上，将滚子细端补偿用坡度曲线过渡，过渡部分长度为重合部分的一半，如图8所示.这样，细端部与地面接触时会逐渐过渡地进入接触.②滚子中部变形变化不大，为避免滚子直径整体增大，可将最小变形补偿定为0，以此为基准点，向上补偿.

修正后，滚子外廓母线曲线与原曲线的对比如图9所示.

图8 滚子两端补偿示意图Fig.8 Compensation sketch map on roller ends

图9 滚子外壳轮廓补偿前后曲线Fig.9 Original and Compensation Curves of Roller Cover

3.3 补偿后滚子橡胶外壳的仿真计算

外壳受力方向垂直于法面，滚子轮廓补偿后，由于外廓曲线改变，受力方向稍有改变，且细端端部受力变小.经仿真计算，其变形如图10所示.可以看出，对变形较大的地方进行厚度补偿.与图6比较可知，补偿轮廓后滚子外壳受载变形后更接近于理论弧线，要合理得多.

图10 滚子外廓补偿后仿真云图Fig.10 Deformation Contour of Compensated Cover

3.4 滚子橡胶外壳变形量与壳体厚度、载荷的关系

滚子橡胶外壳的变形量与很多因素有关，上述补偿计算在特定的条件——壳体厚度15mm和满载25kN下给出.如果载荷或者外壳厚度设计变化，则外壳变形量要相应变化，对外壳的补偿量也要做相应改进.以下对外壳不同厚度、受不同载荷时进行仿真.只在外壳大端局部加载时，计算大端的最大变形.图11，12为滚子橡胶外壳变形量与壳体厚度、载荷的关系曲线.

图11 橡胶外壳变形量与载荷关系曲线Fig.11 Roller cover deformation curve to load

图12 橡胶外壳变形量与壳体厚度关系曲线Fig.12 Roller cover deformation curve to cover thick

从图11和12可以看出，橡胶外壳变形量与载荷呈线性关系，而与外壳设计厚度呈非线性关系.当载荷或外壳厚度改变时，可以根据插补方法选取适当的补偿量，提高精度.另外，外壳变形量还与材料、外壳形状等有关，具体设计时都应该加以考虑.

3 滚子变形试验

对设计的滚子进行试验测试，分别测量滚子不同部位加载后的变形.图13为滚子变形试验图，图14为不同部位的测试变形量.可见，在同样载荷条件下，两端的变形要大于中部变形，与仿真结果一致.但由于Mecanum轮结构复杂，安装后不便测试，试验条件和仿真条件有差别，如试验测试时加载面积小、载荷方向垂直于轴线等，使得试验数据与仿真结果不能定量对比.

图13 滚子变形试验图Fig.13 Test of roller deformation under load

图14 滚子外壳不同部位的变形量测试结果Fig.14 Measured deformation of cover on different position

5 结论

本文采用的Mecanum轮滚子轮廓补偿法逻辑清晰、科学合理.试验测试证明该设计有效，已经应用于全向移动平台的Mecanum轮设计.文中滚子外廓补偿是在特定的条件下计算得出的，当与本文条件不符时，可以采用文中提出的方法作适当修正，以设计出满足自身精度要求的滚子外壳.

［1］SALIH J E M，RIZON M，YAACOB S，et al.Designing omnidirectional mobile robot with mecanumwheel［J］.American Journal of Applied SciencesⅢ，2006（5）：1831－1835.

［2］WOODS B.Omni－directional wheelchair［D］.Perth：University of Western Australia，2006.

［3］DOROFTEI I，GROSU V，SPINU V.Omni－directional mobile robot－design and mecanum wheel designbioinspiration and robotics：walking and cimbing robots［M］.Vienna：I－Tech Education and Publishing，2007.

［4］DOROFTEI I，GROSU V，SPINU V.Omni－directional mobile robot－design bioinspiration and robotics：walking and climbing robots［M］.Vienna：I－Tech Education and Publishing，2007.

［5］FENELLI N，MULLOWNEY R.Omni－directional wheels and methods and vehicles employing：US，US2005／0183896A1［P］.2004－12－30.

［6］FIEGELl O，BADVE A，BRIGHT G，et al.Improved mecanum wheel design for omni－directional robots［C］.Berlin：Springer，2002.

［7］DICKERSON S，LAPIN B.Control of an omni－directional robotic vehicle with mecanum wheels［C］.Piscataway：IEEE，2006.

［8］KANG S H，ZHANG X L，XIE Y.Mechanics analysis of onidirectional mecanum－weel based on FEM ［J］.Applied Mechanics and Materials，2013，271：1012－1016.