地质钻机定点钻孔加载稳定性评价方法
黄子斋,赵静一,李见卿,唐 园,郭传新
(1.燕山大学 机械工程学院,河北 秦皇岛 066004;2.北京建筑机械化研究院,北京 100007)
定点钻孔是通过钻机钻进使钻具到达指定目标点位置以完成修复或改良施工的工法,主要用于对坝体、防渗墙和边坡等混凝土或岩土介质所产生的内部裂隙进行定点钻孔,成孔后通过灌注混凝土对裂隙进行修复或改良地质.随着地质探测技术的不断发展,现阶段已可实现对内部结构和裂隙的精确探测并可检测和引导钻具到达指定位置,如图1所示.定点钻孔具有工法简便、破坏区域小、成本经济和快速准确等优点,得到越来越多的重视和运用.由于对成孔质量和偏斜有着较高精度要求,一般采用定载定速钻进,即固定加载力和钻头转速.这对施工钻机的性能提出了较高的要求.

图1 定点钻孔修复裂隙Fig.1 Fixed-point drilling to repair fracture
现阶段,在钻孔前需对使用一定时间后的工程钻机的加载稳定性进行评估.通常做法为:钻孔前对相近介质试钻,将钻机设置为该项定点钻孔施工的设计载荷和转速,然后对载荷压力值进行检测,压力波动较大的设备为不合格.该方法由于缺乏必要的理论模型使评价存在较大的不确定性.鉴于此,本文提出一种具有科学性和可操作性的钻机定点钻孔载荷稳定性评价方法,不仅能对钻机在施工前进行性能评估,还可对某段时间内的钻进过程进行加载性能监测,有着较好的实际工程意义.目前,对加载性能的研究较多,并取得一定成果,主要研究方向有加载性能的试验仿真和数值模拟[1-2],还有定性分析液压系统的故障失效[3].但对定点钻孔载荷稳定性评价方法的研究较少,尚无可直接借鉴的模型和方法.
本文根据岩土钻掘工程学原理,结合模糊数学理论建立系统性能模糊化分析的数学模型,给出一定速度和载荷控制下的载荷稳定性隶属函数.同时,采用工程数据采样及数理统计的分析方法对样本进行处理,并针对具体工程实际建立数据样本,运用MATLAB软件进行数据处理和求解,最终得到一定寿命条件下满足某工况要求的性能函数,以研究工程钻机定点钻孔载荷稳定性的模糊化分析评价方法.
1 裂隙修复钻孔工程学原理与加载系统
在定点钻孔工况下,所钻介质相对均匀,载荷与钻进速度往往处于Ⅲ区(体积破碎区),以使其保持较高的钻进效率[4].为了保证能够准确到达所要灌注修复的裂隙处,根据阿里莫夫静载荷与钻进速度的曲线关系,施工钻进应保持一定载荷,以保证孔的垂直度和孔内质量[5].如果施加载荷压力过大或不稳,钻进时极易发生偏移和孔内塌陷,使钻头偏离原定方向而不能到达裂隙,如图2所示.
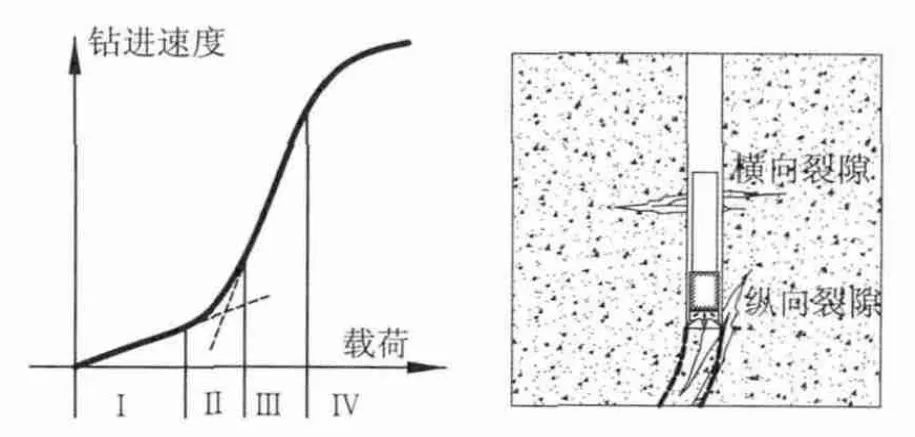
图2 钻进速度与加载曲线与钻孔中的裂隙Fig.2 Drill speed and pressure curve and fracture

图3 钻进加载系统与LUDV原理Fig.3 Drill hydraulic system and LUDV
钻进加载系统(如图3)由变量泵1、旋转马达控制单元2、高性能加载油缸(或马达)3、压力控制单元4和负载独立流量分配阀控单元5组成.旋转马达控制单元能够输出稳定转速和大扭矩;加载油缸或马达拖链进给提供钻进所需的载荷;压力控制单元对载荷进行无级有效的精确控制.采用液压LUDV(Load Independent Flow Distribution)独立流量分配技术使系统的加载压力与负载无关而保持一定的钻进速度.
2 加载性能数学模型
2.1 加载性能模糊化数学模型
施工过程中钻进速度或是加载力变化是分析钻进系统性能的关键.影响性能的因素较多,最主要的因素是系统设计的匹配以及系统磨损而导致的泄漏等.这些因素使钻进系统无法处于优良性能区间运行,不能满足较高的施工要求[6].
加载性能分析时并不能精确判定某一状态为优良还是较差.对工况要求的满足问题因施工设计的差异有所不同,一般的性能描述方法是“0,1”的关系,即满足或不满足.在实际应用中,性能对要求的符合程度具有较大的模糊性,取值可在0~1之间.另外,过渡区间的描述具有较大的模糊性,准确定义较困难,所以运用模糊理论的研究方法更加符合实际[7-8].
可设载荷稳定状态的固有特性为模糊量,令Э(0,+∞)为模糊子集;用(x)表示固有载荷稳定状态的模糊子集的隶属函数,则该载荷稳定状态的模糊性能概率可由式(1)确定:
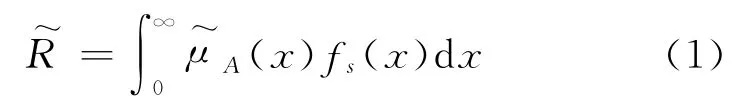
式中:fs(x)为系统工作H0小时后随x变化的压力分布函数.
2.2 隶属函数的分析与确定
如图4所示,静载荷处在Ⅲ区(体积破碎区)时,载荷与钻进速度可视为成线性比例关系,即若设定某一钻进速度,其必定有且只有唯一对应的载荷.由此,根据模糊数学理论,建立钻进载荷变化对系统性能影响的模糊化关系,运用待定系数法确定该隶属函数(x).由于其优良线性特性,可选取三角型分布形式为性能模糊隶属函数.
当静载荷值为F0时,钻进速度达到最佳速度v0,此时成孔质量最好,加载性能为最佳状态,记为1.实际工程中很难较精确得到最优加载力F0,可采用节点法解决:一般情况下工程设计方将预先给出一个较优加载力范围(F1~F2),其相对应的加载系统压力为(p1~p2).确定(p1~p2)为钻进性能的优良压力范围,并设定为优良性能区间的两个过渡模糊点.设优良性能区间隶属度应不小于“0.9”,即得到“大约0.9”的节点.一般情况下:
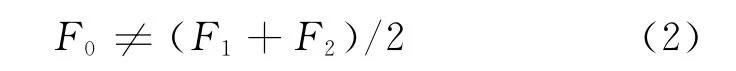
F0不一定是(F1~F2)的中点值,所以隶属函数还不能确定,需要其他条件.
因此,以“跨越点”——隶属度为“0.5”的点,其对应的加载系统压力值为(p3,p4).设定钻进速度由预设状态“相”变化到速度改变且稳定“相”的相邻两相的中间值为“大约0.5”的节点[8],如图4中的分布曲线1所示.可在未确定隶属度为1的F0节点的情况下,得到性能三角型分布的模糊隶属函数.三角型分布模糊隶属函数并不是固定不变,需要为适应不同地层的施工要求预设相应的最优加载范围(F1~F2).随着其对应的最佳载荷值F0的不断增大,隶属函数也在不断变化,如图4中曲线1,2,3所示.但其a1,a2临界点所确定的压力区间则基本处于第Ⅲ区的压力范围内.
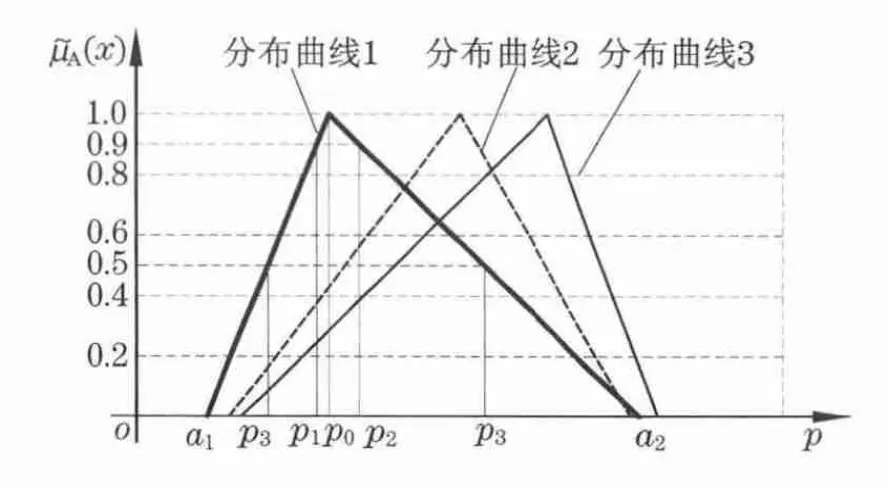
图4 隶属函数分布曲线Fig.4 Distribution curve of membership function
已知(p1,p2,p3,p4),由此可得到隶属函数(x):
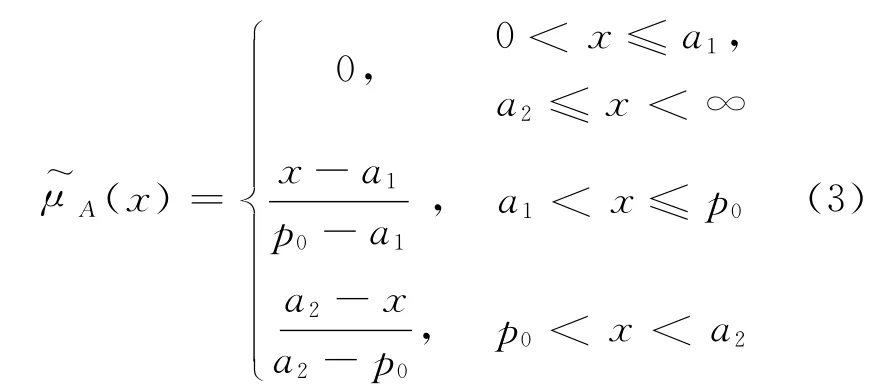
其中,由直线方程

式中:δ为曲线1上a1p0段斜率.
可得:
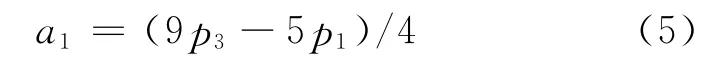
同理可得:

可计算得出:

将式(4)—(7)带入式(3),整理得节点法模糊隶属函数(x):
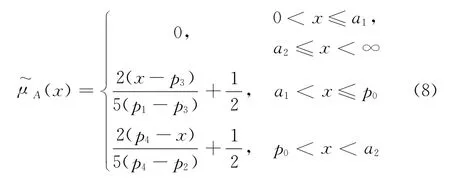
由式(8)可知,在节点法所确定的隶属函数中,参数仅有(p1,p2,p3,p4),该方法使计算大大简化,并且更为重要的是其参数值也较容易得到.
2.3 对样本数据的概率分布处理
要描述某工作时期钻进载荷的稳定性是否满足此次施工工况的要求,应选取相应的试验钻孔时间区间.样本设计及数据的采集方案为:
(1)在岩土钻机液压钻进系统无故障维修条件下工作H0小时后,进行时长为t的压力信号数据采集.测压点位于加载油缸的进出油口,以减小管路损失和干扰,确保数据的有效可靠.
(2)根据实际情况及数据采集设备的要求确定采样频率M.
(3)采用多样本数据方法,提高样本准确性.在同一施工地点,选取相邻的n个施工孔进行数据采集,得到n组样本数据S,建立压力波动图,如图5所示.压力波动图可以直观地表示出样本数据的异常情况以及可初步辨别样本的有效性.
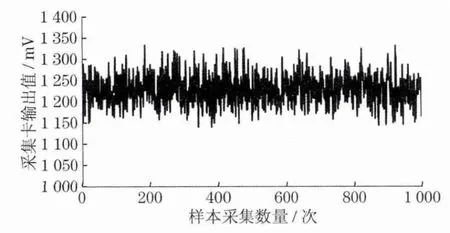
图5 钻进压力波动图Fig.5 Pressure fluctuations in drill
仅根据压力波动图是无法进行实际操作的,要得到可进行计算的分布函数fx(x),需要运用数理统计学方法对样本数据进行数据处理.其具体方法如下:
(1)频数计算.结合n个数据样本制作n行矩阵,其中n组样本空间数据个数应一致,对矩阵进行频数计算,以频数图的方式表示出来.
(2)参数估计.由频数图初步估计样本数据近似服从某一分布规律形式.经过统计计算得到分布函数的参数估计以及置信水平下的参数置信区间.
(3)对计算得到的分布函数的参数作某种假设,根据样本观察值,检验假设是否正确以及决定是否接受假设.
如果“假设结果”为“不能拒绝假设”,所估计的分布函数参数则具有较高的合理性,进而得到分布函数的计算表达式,即所测时间节点处的系统压力波动的分布函数fx(x).
以图5样本数据为例,其经过数据处理可得到一个样本矩阵S(x),每组有2 000个数据,共10组:

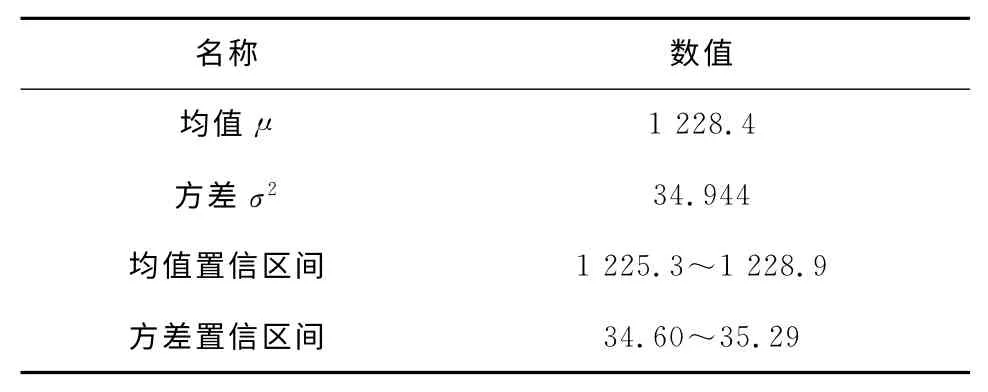
表1 计算值Tab.1 Calculated
图6为其频数图.根据图6可初步确定,分布函数fs(x)大致服从正态分布.由此,将所得数据即数据矩阵按正态分布的计算方法进行参数估计.运用MATLAB软件计算得到数据样本矩阵的均值μ、方差σ2及α=0.05的置信区间,如表1所示.其中α=0.05为一般置信区间标准,在解决实际工程问题时,往往由设计者根据实际需要进行调整,一般为0.08~0.01之间.进行方差为未知条件下均值的假设验证,检验结果布尔变量h=0,表示不拒绝零假设,即提出均值为1228.4的假设是合理的;α=0.05的置信区间为[1 225.3,1 228.9]完全包括1 228.4,精度较高;sig=1,≥0.5,不能拒绝零假设.因此,某型钻机使用时间约为1 800h,后其钻进系统的压力波动分布函数为
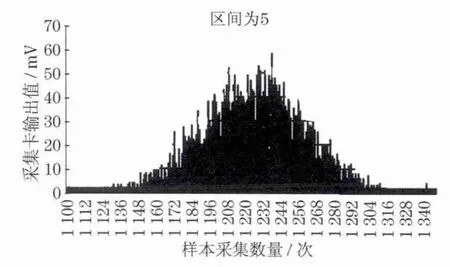
图6 数据频数图Fig.6 Frequency chart for data

3 算例计算
某型钻机使用时间约为1 800h,对某农业水库坝体进行钻孔加固施工.孔深约20m,倾角25°,成孔垂直精度≤±5°.须评定定点钻孔加载载荷稳定性是否处于优良状态,对其样孔试验钻孔进行数据采样.已知参数为使用时间H0=1 800h;压力值p1=17.5MPa;压力值p2=19.2MPa;压力值p3=15.8MPa;压力值p4=22.7MPa;单次采样时间T≈20min;采集组数n=10.
压力传感器输出电流为4~20mA,压力量程为0~60.0MPa,分辨率为12位,输入范围为0~20mA,输出值0~409 6,最高采样频率500Hz.转化公式为
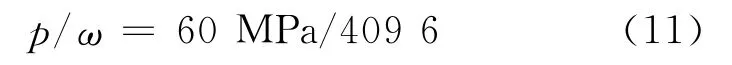
式中:ω为压力值,p为采集卡输出值.
将(p1,p2,p3,p4)=(1 194,1 131,1 079,1 549)代入(3)~(10)式,然后代入式(1),联合分段积分可得:
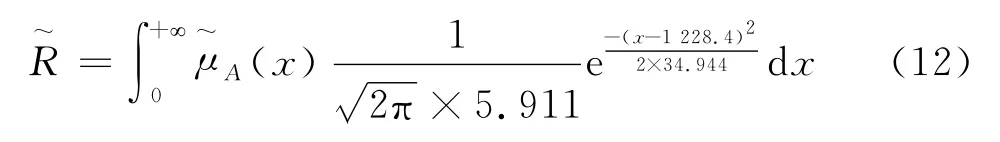
计算得=0.920 3.即载荷性能此时处于优良性能状态的概率为0.920 3.工况要求性能优良概率高于0.90,即满足.因此该型钻机钻进加载系统在使用约1 800h后,其性能状态对于所要完成的施工工况可视作满足要求.
4 结 论
(1)地质钻机定点钻孔的载荷稳定性是一个相对性问题,受钻机工作寿命、地质条件以及工况要求等因素影响,其计算模型应体现该因素的实时性.其次,模糊分析法解决了钻进系统是否处于优良性能这一模糊概念的数值量化问题.由已知数据确定隶属函数,不需要知道隶属函数的极值条件,大大简化了计算.
(2)实例计算分析验证了性能模糊化计算方法行之有效且直观、简便.通过其性能数值,为其节能技术改进设计提供了数据参考.采样区间、模糊点取值、置信区间和采样组数的设定值会对最终结果产生影响,需要在实践过程中不断完善.
(3)本文以加载力的变化情况为研究对象,该方法对地质钻机定点钻孔载荷的稳定性提出了新的评价模型,具有较强的可操作性,具有现实工程意义.由于是对定点钻孔的载荷稳定性评价方法的初步探索,在精确性上还有待于进一步研究.
[1]张锐,王龙鹏,孙保山,等.基于AMESim的多变幅工程钻机负载敏感回转回路仿真分析[J].煤矿机械,2013,34(6):104-105.ZHANG Rui,WANG Longpeng,SUN Baoshan,et al.Simulation analysis on load sensing rotating system of multi-luffing engineering drilling rig based on AMESim[J].Coal Mine Machinery,2013,34(6):104-105.
[2]胡志坚.钻机负载自适应液压控制系统的研究[D].长春:吉林大学,2007.HU Zhijian.Research on load self-adaptive hydraulic control system of rill rig[D].Changchun:Jiling University,2007.
[3]刘英杰,徐兵,杨华勇,等.液压系统负载传感功率匹配与比例控制研究[J].农业机械学报,2010,41(5):182-187.LIU Yingjie,XU Bing,YANG Huayong,et al.Strategy for flow and pressure control of electro hydraulic proportional separate meter in and separate meter out control system [J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(5):182-187.
[4]MCMANUS K J,ALABASTER D.Constant force shaking of a group of four drilled shafts[J].Journal of Geotechnical and Geoenvironmental Engineering,2004,130(2):123-128.
[5]鄢泰宁.岩土钻掘工程学[M].北京:中国地质大学出版社,2001.YAN Taining.Rock and soil drilling and digging engineering[M].Beijing:China University of Geosciences Press,2001.
[6]MCGRAY S.Soil Nailing:DOTs warm up to new technology[J].Better Roads,2003,73(3):72-74.
[7]李士勇.工程模糊数学及应用[M].哈尔滨:哈尔滨工业大学出版社,2004.LI Shiyong.Engineering and application of fuzzy mathematics[M].Harbin:Harbin Institute of Technology Press,2004.
[8]程学进,董玉革,高亮.模糊可靠性分析的等效正态隶属函数法[J].农业机械学报,2006,37(4):111-114.CHENG Xuejin,DONG Yuge,GAO Liang.nalytical method of fuzzy teliability based on equivalent normal membership function[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(4):111-114.

