基于B样条曲线的电脑横机三角优化设计
伍 仲,俞淼轩,王国庆,方 园
(1.浙江理工大学材料与纺织学院,杭州310018;2.绍兴金隆针织机械有限公司,浙江绍兴312030)
基于B样条曲线的电脑横机三角优化设计
伍 仲1,俞淼轩2,王国庆2,方 园1
(1.浙江理工大学材料与纺织学院,杭州310018;2.绍兴金隆针织机械有限公司,浙江绍兴312030)
针对电脑横机三角的轮廓曲线大多由直线和圆弧连接而成,造成三角和织针使用寿命低、机器速度受到受限、整机稳定性差等问题。在运用ANSYS/LS-DYNA对织针和三角进行动力学分析的基础上,采用B样条曲线对原有三角轮廓曲线进行优化设计。优化设计后,三角和织针相互间的冲击作用明显降低。
横机三角;ANSYS/LS-DYNA;B样条曲线;曲线优化
0 引 言
电脑横机作为精密的机电一体化设备,三角是其成圈机构的重要组成部分。三角被嵌放在机头上,随着机头的移动,并带动针槽中织针上下运动,完成编织[1]。因此,三角和织针可以看做是特殊的凸轮机构。在凸轮机构中,凸轮的轮廓直接决定着从动件的运动轨迹、相互作用力大小。因此,为了保证凸轮机构的精确性和稳定性,凸轮的轮廓曲线必须进行有效的设计[2]。现在大部分的横机三角轮廓曲线多由直线-圆弧构成,这样的三角加工简单,但在运动过程中,织针和三角的相互冲击较大,从而引起织针使用寿命低下、横机速度受到限制、横机整机稳定性差等缺陷[3]。为了改善横机的上述缺陷,必须对横机三角轮廓曲线进行重新设计。
与凸轮的轮廓曲线设计类似,对于三角轮廓曲线设计的优化,主要是根据织针的运动与三角的受力特征,选取合适的运动节点,将这些节点通过合适的曲线连接起来,获得动力学特性优异的复合曲线,从而设计出合理的三角[4]。现在对于横机三角轮廓曲线的研究,主要是通过使用合适的曲线,如摆线、多项式曲线等,对原有的直线-圆弧三角进行修正,使织针能够具有更加优良的动力学性能。LS-DYNA作为模拟机构瞬态动力学软件,能够有效地模拟运动过程中横机三角与织针之间的相互作用,并能得到有限元模型和相应的实验数据,为横机三角的设计提供良好的力学分析基础。而B样条曲线具有几何不变性、凸包性、保凸性、变差减小性、局部支撑性等许多优良性质,它能控制曲线通过一系列的空间点,来决定曲线的外形,从而获得具有优良动力学性能的三角轮廓曲线。
1 基于ANSYS/LS-DYNA的横机三角动力学分析
横机三角与织针之间的相互作用是典型的非线性接触-碰撞问题,可以利LS-DYNA强大的非线性动力分析功能来进行三角与织针之间的动力学分析。
1.1 基于ANSYS/LS-DYNA建立横机三角有限元模型
横机的三角主要由起针三角、横档三角、压针三角构成,三角的轮廓曲线大致就是织针的运动轨迹,图1是常见的横机三角。

图1 常见电脑横机三角
为了使用ANSYS/LS-DYNA对横机三角进行仿真模拟,首先要建立三维模型。建模采用自下而上的步骤进行,即通过底层的图元构造上层模型,最终构成关键点(key point)-线(line)-面(area)-体(volume)的层次关系。建模过程中需要使用ANSYS程序提供的完整的布尔运算,进行相加、相减、相交、分割等建立实体模型。最终建立的三维模型如图2所示。
1.2 三维模型ANSYS/LS-DYNA结果分析
建立三维模型后,需将这个模型导入到LS-PREPOST中,进行后处理分析。通过LS-PREPOST的后处理,可以得到图表等方式,直观描述三角和织针之间在接触-碰撞过程中的相互作用,如接触-碰撞过程中的应力-应变曲线、位移、速度、加速度等都可以用图表等直观描述。图3是织针的运动状态曲线。
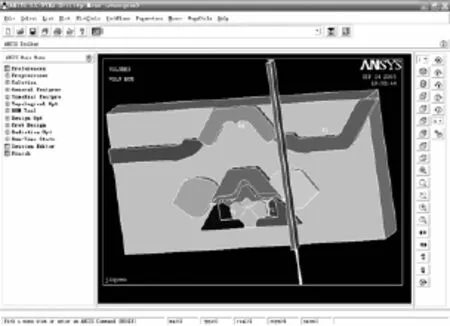
图2 横机三角三维模型
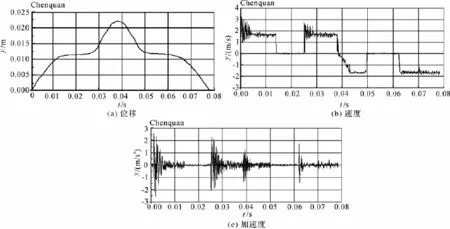
图3 织针运动状态曲线
从图3(a)可以看出,织针的位移曲线与三角的轮廓曲线是一致的,说明织针按照三角轨道运动,织针与三角之间存在接触和碰撞。由图3(b)和图(c)可以发现,织针运动到三角的直线和圆弧过渡区域,如0~0.005 s、0.025~0.3 s、0.035~0.04 s等时间段内织针的速度和加速度都发生了比较剧烈的波动。根据物理学原理,此时织针和三角之间会产生很大的冲击应力以及剧烈的振动作用,从而造成三角和织针使用寿命低、机速提升受限、整机稳定性差等问题。因此,由直线和圆弧连接而成的三角的设计是不合理的。
2 非线性三角的优化设计
基于直线-圆弧曲线三角存在较大的缺陷,有必要开展对非线性成圈三角的研究。非线性成圈三角设计原理是根据织针在成圈过程中的工艺要求和受力特点,综合考虑织针的运动轨迹和织针与三角之间的相互作用力,建立相应的数学模型来优化三角曲线的设计。由于一般非线性三角和针踵冲击点的斜率总是比较小的,使得冲击强度也将相应的较小,它能使织针具有平稳而连续的加速度,或者将其变化限制在一个极小的范围内,从而减少了织针的断裂,降低了三角磨损,为提高横机的效率创造了有利条件。
采用曲线对三角轮廓设计进行优化,同直线-圆弧组合曲线一样,是根据织针的运动与三角的受力特征进行分析和比较,将不同特性的曲线与直线连接组成复合曲线。常见的几种曲线有:摆线曲线、双谐曲线、多项式曲线、简谐曲线等等,使它们同直线相组合,形成组合曲线,通过优化设计来获得动力学特性优异的复合曲线,从而设计出合理的成圈三角。本文采用直线-B样条曲线对三角曲线进行优化设计。
2.1 基于B-样条曲线的非线性三角优化设计
2.1.1 样条函数的定义
在计算机辅助设计系统中,一般控制曲线通过一系列的空间点,来决定曲线的外形,这些曲线叫自由曲线或Bezier曲线。Bezier曲线有很多缺点,如曲线或曲面不能作局部修改、曲线或曲面的拼接比较复杂等。为了有效控制和设计这些曲线,Gorden等将Bezier的基函数换成样条函数,从而构造了等距离节点的样条曲线,也称为均匀B样条曲线。
B-样条曲线是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是Bezie曲线的一种一般化,可以进一步推广为非均匀有理B样条(NURBS),使得我们能给更多一般的几何体构建精确的模型。B样条曲线曲面具有几何不变性、凸包性、保凸性、变差减小性、局部支撑性等许多优良性质,是目前CAD系统常用的几何表示方法。
B样条曲线的方程定义为:
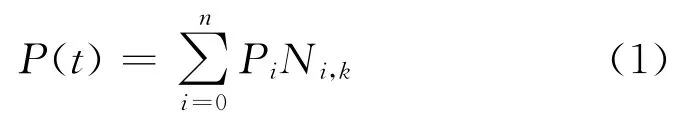
式中:Pi(i=0,1,…,n)是控制多边形的顶点;Ni,k(t)(i=0,1,…,n)称为k阶(k-1)次B样条基函数。
B样条基函数是一个称为节点矢量的非递减的参数t的序列所决定的k阶分段多项式,也即为k阶(k-1次)多项式样条。一般用下式定义节点矢量
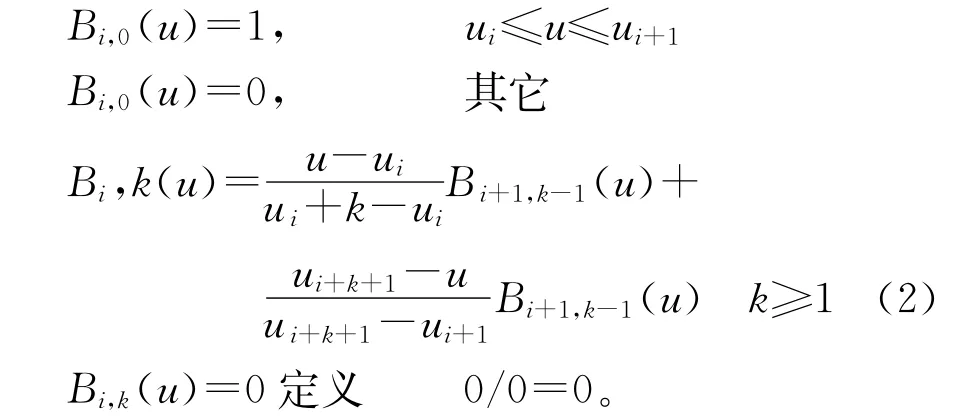
此时若令k=3则为三次均匀样条曲线的表达式。此时曲线通过一个控制点,并与首、末边相切。
2.1.2 横机三角的优化设计
为了对横机三角重新进行曲线设计,首先要考虑织针在成圈过程中的工艺要求和受力特点,使设计后的曲线依然能保证织针正常工作。此外还要考虑织针与三角之间的相互作用力,使织针在最佳的运动条件下运行,具有平稳而连续的加速度,或者使其加速度在较小的范围内变动,从而降低织针与三角的相互冲击,提高横机稳定性。
以起针三角和顶针三角的过渡段为例,对三角的轮廓曲线进行重新设计。曲线重新设计开始后,首先要根据三角的工艺条件确定控制点。可以根据织针在成圈过程中的位移值,得到数据点xi(i=0,1,2…,n),这些数据点一般是不均匀的,必须进行参数化,可以采用弦长参数化,即:
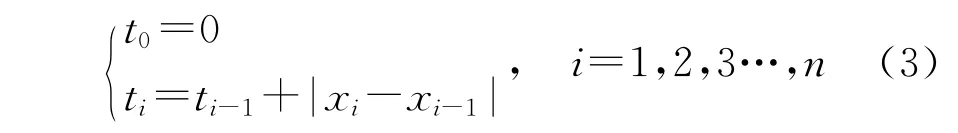
然后将这些参数化结果运算:
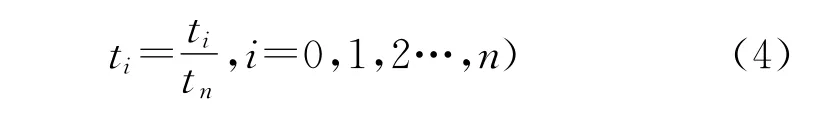
则[to,tn]=[0,1],此时非均匀样条曲线可以写成如下表达式:
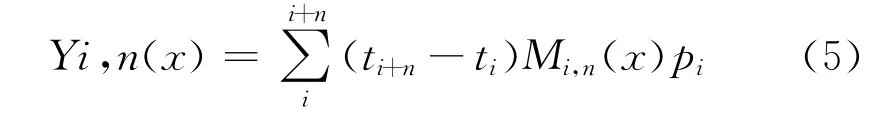
式中:i为第i段曲线,Pi为控制点。
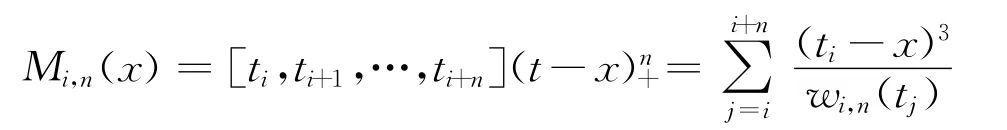
将工艺点参数化后,B样条曲线的表达式可以写成如下形式:
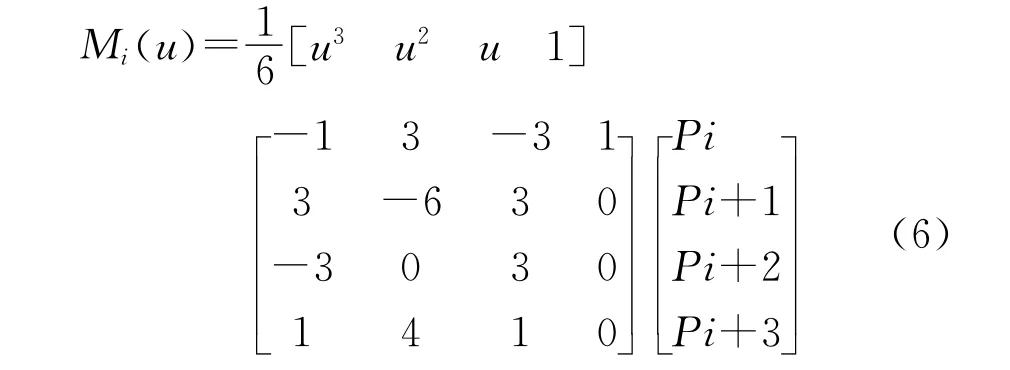
式中:u是参数且u∈[0,1];i是第i段曲线,i=0,1,2…,n-3;Pi为第i个控制点。
得到控制点后,可以有不同方法生成样条曲线,如图4中(a),(b)所示。在图(a)中是常规地将各个控制点带入到基函数中得到曲线。而在图(b)中是将控制点所构成的多边形的各条边等分,然后将中点连接并使之依次通过首末控制点。图(a)和(b)所构成的曲线是等价的。从上述构造方法可以看出通过控制首末点以及首末点的切线方向就可以控制样条曲线的形状。
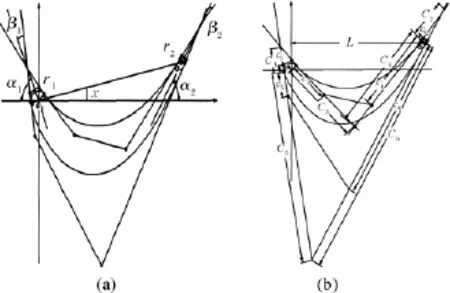
图4 生成B样条曲线
在顶针三角和压针三角的过渡段曲线重新设计中,主要是将原来的两条直线过渡段替换为B样条曲线过渡段。首先根据织针的工艺要求找到织针的若干个工艺运动点,并将这些点参数化,得到了控制点V0,V1,V2,V3……(见图5),根据B样条曲线的生成方法,得到B样条曲线的端点P0,P1,P2,P3……,将这些端点连接就得到了B样条曲线过渡段。图5是选取四个工艺点时,生成的B样条曲线,通过控制V0V1和V2V3所在直线的斜率或者增减控制点的数量,就可以控制B样条曲线的形状。
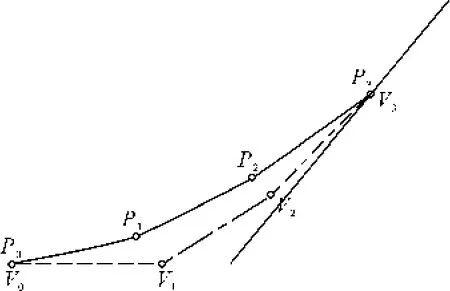
图5 起针三角和顶针三角过渡段曲线设计
此时每一段的表达式如下:
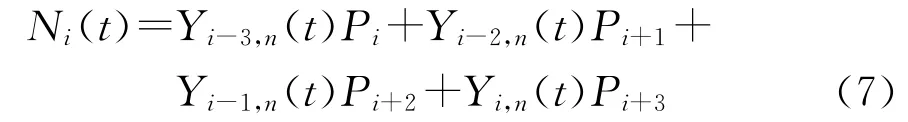
式中:t为参数化后的工艺点;Y(t)为样条曲线基函数。
通过对上述每一段的曲线求导,可以得到织针在这一段上的加速度,从而初步验证曲线设计是否合理。求导递归公式如下:
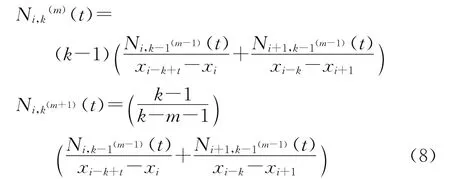
得到曲线后按照1.1所述方法进行有限元建模,并对模型进行后分析,得到相应的数据参数,将它们与直线-圆弧三角模型进行对比。对比内容主要是织针运动的轨迹能否达到成圈要求,织针速度和加速度的变化在连接段是否有显著地趋缓等。如果达到要求则这条曲线就是可行的三角轮廓曲线;若达不到要求则需对曲线进行重新设计,直到达到设计要求为止。
2.2 改进后的结果分析
通过对曲线进行重新设计,得到相应的直线-B样条曲线三角轮廓曲线,并建立三维模型。为了对改进后织针的运行状态进行分析,将改进后的三角建立三维模型并进行仿真分析,得到了织针在改进后三角作用下的位移、速度和加速度的变化情况。
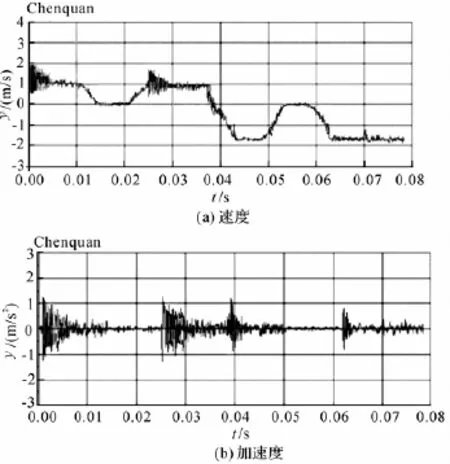
图6 改进后织针运动状态
图6是改进后织针的运动状态曲线。由图(a),(b),可以发现织针在0~0.005 s、0.025~0.03 s等时间段内,即各三角连接过渡区域内,织针的速度、加速度变化趋缓,表明改进后的三角可以有效降低织针的冲击应力和振动。
以起针三角和顶针三角过渡段为例,图7所示为直线-圆弧顶针三角DM直线段。
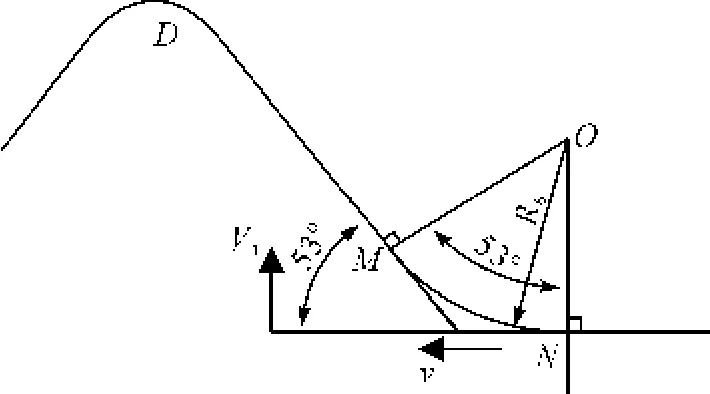
图7 改进后的顶针三角
假设针踵在M点处与顶针三角接触,成圈编织过程分析时取三角在水平方向的速度为恒速1.2 m/s,三角角度为53°,所以可得:
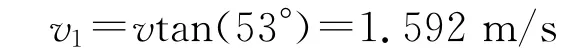
设此时织针的应力为σ,则:
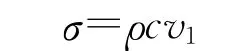
式中:ρ为织针的密度(7.85×103kg/m3),c为应力波在介质中的传播速度(5 200 m/s)。
则织针在这段上的最大冲击应力为
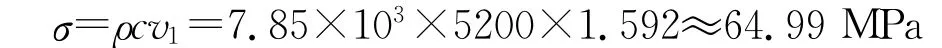
在改造后的三角中,通过选取若干工艺点,并将这些点参数化,得到了若干控制点(如图5中的曲线所示),然后通过B样条曲线构造方法得到了MN段曲线,即用MN段样条曲线代替了原有三角的折线,通过测量,MN段上的最大三角角度为30°,此时最大速度为:

则织针在这段上的最大冲击应力为,
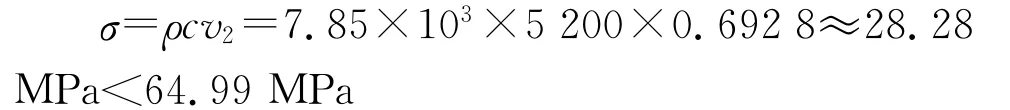
可以发现织针的最大冲击应力下降了60%左右。
同理在各三角的连接区域,通过使用B样条曲线重新设计轮廓曲线,能使织针的速度和加速度都有较大的趋缓,此时织针和三角之间的冲击、振动都会趋缓,说明使用B样条曲线设计后的三角的动力学特性是优于直线-圆弧三角的。
3 结 论
a)采用B样条曲线对直线-圆弧三角轮廓曲线重新设计,织针的运动状态曲线和原有的运动状态曲线基本一致,说明使用B样条曲线对直线-圆弧三角轮廓曲线重新设计是可行的。
b)采用B样条曲线对直线-圆弧三角轮廓曲线重新设计后,织针在0~0.005 s、0.025~0.03 s等时间段内,即各三角连接过渡区域内,织针的速度、加速度变化趋缓,如在起针三角和顶针三角过渡段,织针的最大冲击应力下降了60%左右,说明重新设计后的三角轮廓曲线,可以有效降低织针在各三角过渡区域的冲击应力和振动作用,这有利于解决横机三角和织针使用寿命低、机速提升受限、整机稳定性差等问题。
[1]方忆湘,刘文学.基于几何特性的三次均匀B样条曲线构造描述[J].工程图学学报,2006,(2):96-102.
[2]刘延柱,薛 纭,陈立群.弹性细杆平衡的动态稳定性[J].物理学报,2004,53(8):2424-2428.
[3]刘正芹.横机退圈过程的力学分析[J].青岛大学学报,2001,16(2):29-31.
[4]彼得·艾伯哈特,胡斌.现代接触动力学[M].南京:东南大学出版社,2002:215-217.
[5]张胜民.基于有限元软件ANSYS 7.0的结构分析[M].北京:清华大学出版社,2003:369-371.
[6]万小朋,龚 伦,赵美英,等.基于ANSYS/LS-DYNA的飞机机翼前缘抗鸟撞分析[J].西北工业大学学报,2007,25(2):285-288.
[7]李艳霞.针织机三角的计算机优化设计[D].天津:天津工业大学,2002.
[8]Jeong K Y,Kim Y B,Dynamic modeling of the latch Needle cam system of weft knitting machines[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2003,217(2):219-227.
[9]Duana Y,Keefeb M,Bogettic T A,et al.Finite element modeling of transverse impact on a ballistic fabric[J].International Journal of Mechanical Sciences,2006(48):33-43.
Optimal Design of Cam of Compute Flat Knitting Machine Based on B-spline
WU Zhong1,YU Miao-xuan2,WANG Guo-qing2,FANGYuan1
(1.College of Materials and Textiles,Zhejiang Sci-Tech University,Hangzhou 310018 China;2.Shaoxing Jimlong Machinery Manufacturing Co.,Ltd,Shaoxing 312030,China)
In allusion to such problems as short service life of cam and knitting needle,limited machine speed and poor machine stability caused by the situation that the profile curve of cam of computer flat knitting machine is mostly connected by straight line and arc,this paper conducts optimal design of the original profile curve of cam using B-spline on the basis of conducting kinetic analysis on knitting needle and cam by using ANSYS/LS-DYNA. After optimal design,the mutual impact effect of cam and knitting needle greatly reduces.
cam of flat knitting machine;ANSYS/LS-DYNA;B-spline;curve optimization
TS183.42
A
(责任编辑:张祖尧)
1673-3851(2014)01-0024-05
2013-07-05
伍 仲(1988-),男,湖南长沙人,硕士研究生,主要从事针织机械研究。通信作者:方 园,E-mail:fyuan123@126.com

