煤液化多相流输送管道冲蚀磨损分布预测及分析

偶国富，龚宝龙，李伟正，包金哲，金浩哲

（浙江理工大学流动腐蚀研究所，杭州310018）

煤液化多相流输送管道冲蚀磨损分布预测及分析

偶国富，龚宝龙，李伟正，包金哲，金浩哲

（浙江理工大学流动腐蚀研究所，杭州310018）

针对煤化工中多相流管道系统的冲蚀磨损问题，运用Fluent软件构建流体动力学模型，获得磨损速率与管道位置的关系，用来预测磨损减薄的主要区域。数值计算结果表明：随着管道直径的增加，其最大磨损速率降低；曲率半径为3倍公称直径时，弯头的磨损率较小且均匀；颗粒形状越接近于球形，磨损率越低；当磨损颗粒粒径小于200μm时，磨损率随着粒径的增大而增大，当粒径超过200μm，磨损率几乎不再变化。对原管道系统进行设计改造，提出了一种结构优化改进方案，计算模拟结果显示优化方案可使其磨损率减小为约原来的1/2。

煤化工；多相流管道；冲蚀磨损；失效分析

0 引 言

能源是社会发展的基础和重要因素，充足的能源供应是实现经济可持续发展的关键。近年来，由于能源、化工品的需求日益增大，石油市场上供需矛盾日益尖锐。发展现代煤化工已成为国家能源战略安全的重要组成部分［1］。

煤液化工艺过程多变、工况苛刻、介质复杂，且处于高温、高压环境之下，整个输运系统呈现出较为复杂的流变特性［2］。由于输送的物料有固体颗粒存在，会使管道系统产生严重的磨损，长时间运行之后容易磨损破裂，严重威胁了企业的长周期安全生产［3-4］。煤液化管道系统由于尚无完备的设计规范和选材导则，工程上一般通过增加管道壁厚和提升管道材质来提高管道的安全运行系数，但仍难以保障其长周期稳定运行［5］。

本文针对煤液化加氢反应器至热高压分离器之间的典型含固多相流管道的冲蚀磨损问题，对管道系统进行几何建模和仿真分析，探讨其磨损分布规律。通过改变管道结构及固体颗粒特性等，模拟分析影响其磨损的主要因素，提出多相流管道系统的结构优化方案，可为现场管道结构改造提供参考。

1 多相流管道计算模型

1.1 几何模型和边界条件

煤液化加氢反应器至热高压分离器管道系统从反应器顶部开始，然后延伸到分离器顶部结束。该管道系统共包括7个直管段、4个90°弯管、1个22.5°弯管、1个45°弯管，管道外径为610 mm，壁厚为77 mm，弯管曲率半径均为4倍管道公称直径。其结构尺寸如图1所示。利用Fluent的前处理软件Gambit建立管道的三维模型并划分网格，网格结构如图2所示。

煤粉密度为1 550 kg/m3，粒径为75μm，煤粉规整度主要由颗粒形状系数表示，在0.3～1内选取。入口边界条件设置混合相的湍流强度为2.82%，湍流尺度为0.031 92 m，气相速度为5.17 m/s，液相速度为3.75 m/s，设定液相为第二相，相分率为5.19%，固体颗粒相作为离散相加入流场，起始位置设置于入口端面处，且均匀分布在入射面上，质量流量为10.07 kg/s，入射速度为0；出口处边界条件设置混合相的湍流强度和湍流尺度与进口处的相同；壁面边界条件选用标准壁面函数法和无滑移边界条件；气、液相的密度分别为36.24 kg/m3和826.2 kg/m3，动力粘度为1.3×10-5kg/（m·s）和2.95×10-3kg/（m·s）。

图1 管道系统结构

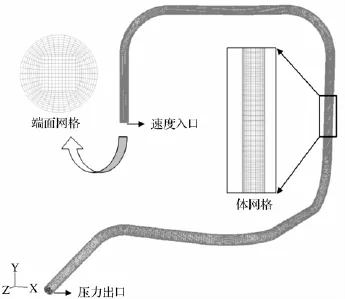
图2 管道网格划分

1.2 基本控制方程

磨损预测的数值计算分三个步骤：首先计算连续相的流场，接着等流场稳定之后再加入颗粒，对颗粒的运动轨迹进行追踪，最后利用颗粒对壁面的冲击反弹关系来计算磨损率。由于本文计算的流场中颗粒相所占的体积百分比较小，所以忽略颗粒与颗粒间的相互作用力。计算所采用的连续性方程和动量方程如下：

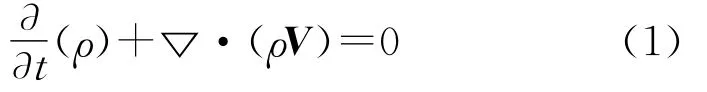
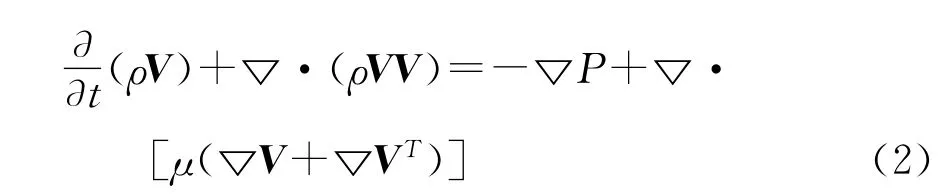
其中ρ是连续相密度，V是速度矢量，▽·（ρV）代表质量通量ρV的散度，μ为介质动力粘度。

1.3 颗粒轨迹模型

采用颗粒作用力平衡方程来计算颗粒轨道，方程表达式如下：

其中FD、FP、FB、FA分别代表曳力，压力梯度力，浮力和附加质量力［6］。

1.4 磨损模型

颗粒冲击管道壁面的过程中伴随着能量损失，这影响了颗粒的反弹轨迹。通常采用冲击-反弹系数来描述这一现象。本文选取Forder等［7］通过实验总结的冲击-反弹恢复系数的公式：

其中θ是颗粒的冲击角度，eN和eT分别代表法向和切向的冲击-反弹恢复系数。

离散相颗粒对管道壁面的磨损率定义式为［8］：

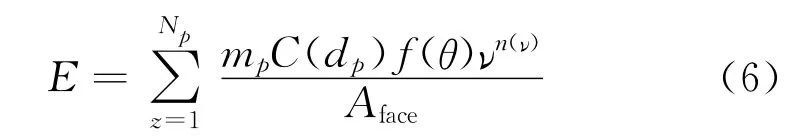
其中E为冲蚀磨损率kg/（m2·s），mp为颗粒的质量流量，θ为颗粒对壁面的冲击角，f（θ）是冲击角度的函数，v是颗粒冲击速度，n（v）是速度指数，C（dp）是关于颗粒直径的函数，Aface是受冲击磨损的表面积。

2 计算结果分析

2.1 磨损速率分布

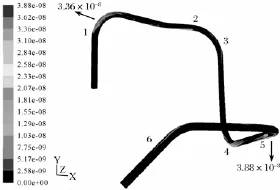
图3 管道壁面磨损分布

计算所得的磨损率分布图如图3所示。由图3可见，磨损率较大的部位主要是管道弯头处，这是由于固体颗粒在跟随管内介质运行至弯头处受到离心力的影响，对弯头处内凹侧面产生冲蚀磨损作用。图3中弯管5处的磨损率最大，实际运行时，对该处管道的壁厚应该重点进行检测。图4和图5分别为弯管1和弯管5处的局部放大图，图中的箭头指向代表介质的流动方向。

图4 弯管1处壁面磨损分布局部放大

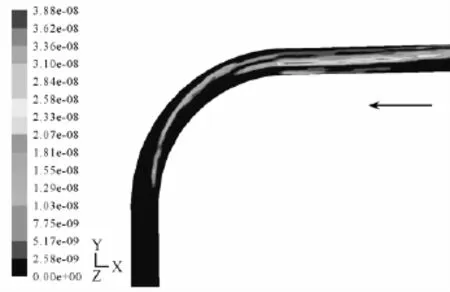
图5 管道5处壁面磨损分布局部放大

2.2 磨损影响因素的分析

含固多相流管道的冲蚀磨损受众多因素影响，如管道半径、曲率半径、颗粒形状系数、颗粒特性等。下文对这些影响因素分别进行分析，为上文所计算管道的优化方案提供理论参考。为了便于描述问题，本文选取弯管1处及与其相连的直管段进行分析。

2.2.1 管径的影响

对DN550、DN650、DN700的管道进行数值计算，取与上述DN600管道相同的介质流量。并将所得的磨损率分布情况与DN600模型的磨损率分布进行对比。管道在弯管1处的磨损率分布情况见图6。计算结果表明，随着管道直径的增大，其最大磨损率逐渐降低。且DN550的管道在弯头处的磨损区域比其它弯管的大，这是由于当介质流量不变时，其管径较小，颗粒在管内的分布密度较大且速度也大，从而加大了颗粒对管道壁面的冲蚀磨损作用。

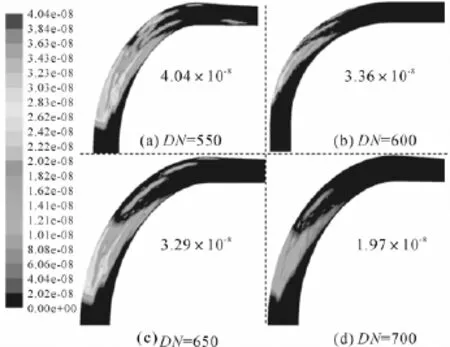
图6 不同管径在弯管1处的磨损速率

2.2.2 曲率半径的影响

曲率半径是影响管道弯头磨损的一个重要因素。在役管道的曲率半径为4，现分别将其曲率半径改成2、3、5和6倍管径（D g）进行数值模拟，各自的磨损分布情况如图7所示。从图7中可知，当曲率半径较小时，其最大磨损率数值较大，这是由于弯管路径较短，油煤浆流动方向改变剧烈，使得弯头外壁和侧壁区域颗粒速度迅速增大，且容易造成颗粒聚集，导致磨损率变大。从图7中还可以发现，随着曲率半径的增大，弯管路径变长，油煤浆流动方向趋于平缓且与弯管处的接触区域范围变大，所以造成弯头处的磨损分布区域加大。综合考虑上述因素，发现在本工况下，R/D=3时，该处弯头的最大磨损率较低，且磨损分布范围较为均匀，有利于延长管道的使用寿命。

图7 不同曲率半径在弯管1处的磨损速率

2.2.3 颗粒规整度的影响

Levy等［9］利用不同形状的颗粒对多种金属材料的冲蚀磨损性能进行研究，发现颗粒形状对材料的磨损率有着重要影响。

对固体颗粒选取4种形状系数k=0.3、0.5、0.7、1进行计算，研究不同规整度的颗粒对弯管磨损率的影响。该管段的磨损分布情况及最大磨损率值如图8所示。由图8可知，在不同规整度的颗粒冲蚀下，该弯管处的磨损分布大致相同，基本分布于管道入口处的内凹壁面。这是由于颗粒受到离心力的影响，致使其偏离介质主流方向，对弯管外壁面产生冲蚀磨损作用。图8还可以发现随着颗粒形状系数的增大，其最大磨损率数值变小。这是因为颗粒形状系数越大，其形状越接近于圆球状，所带有的棱角较少，故而对材料壁面的冲蚀磨损作用减小。

图8 不同颗粒形状系数在弯管1处的磨损速率

2.2.4 颗粒粒径的影响

国内外许多学者曾对颗粒粒径大小对材料的磨损率影响做过研究，发现在一定粒径范围内，随着粒径的增大，材料的磨损率也增大，当粒径超过某一极限值时，粒径对磨损率的影响变小［10］。

本文选取10、74、100、150、200、300μm 6种直径的颗粒进行数值计算，结果见图9。由图9可知，颗粒直径不同，其对弯头内凹造成的磨损分布也不同：粒径较小时，其对弯头外壁面的磨损作用较小，且主要分布在入口处；当粒径逐渐增大，其对弯头处的磨损从入口处逐渐向弯头出口处发展，并布满整个弯头区域。统计该弯头处的最大磨损率值，示于图9中，发现随着粒径的增大，其最大磨损率也增大，当粒径大于200μm时，粒径大小对磨损率最大值几乎没有影响。这主要是因为粒径较小的颗粒所具有的动能较小，其对材料基本不能形成犁削型破坏。另外，当颗粒直径增大到一定程度时，材料受冲蚀的面积也增大，所以单位面积上的磨损率降低。

图9 不同颗粒粒径在弯管1处的磨损速率

2.3 结构优化方案

煤化工过程中由于工艺要求及现场设备布局条件的限制，在管道系统改造时应尽量避免大范围的结构变动。含固多相流管道系统的基本优化思想是，在不改变原有设备系统布局的前提下，通过改变管道走向、管道直径、曲率半径等来减轻管道的磨损情况，而且应该尽量减少弯管数量、缩短管道路径。

图10中虚线部分为原有管道系统布局，实线则为改造后的布局。从图10中可以发现，改造后管道的弯头数量减少了2个，且管道系统的总长度也比改造前的短。根据上文的研究，在保持原有的工况条件不变的情况下，把弯头处的曲率半径变为3倍的管道公称直径有助于降低管道的磨损。

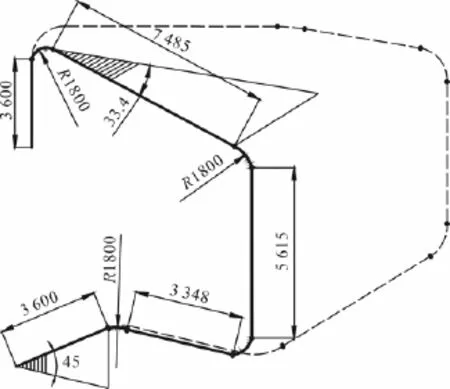
图10 经改造的管道系统结构

图11为改造后的管道磨损率分布。从图11可见，其磨损率最大值仅为1.58×10-8kg·m-2·s-1，次大值为5.27×10-9kg·m-2·s-1，这比原结构中的磨损率最大值降低了约1/2。且改造后的磨损区域分布比较集中，易于实行壁厚的在线监控。

图11 改造后管道系统的磨损分布

3 结 论

a）颗粒对管道磨损相对严重的位置主要处于弯管的内凹侧面部，但是由于管道的走向不同其确切位置又各不相同，在弯管4的底部相对磨损速率达到最大。b）随着管道直径的增加，其最大磨损速率降低；在实际运行工况条件下，弯头曲率半径为3倍公称直径时，弯头的磨损率较小且分布均匀；c）冲击颗粒形状越接近于球形，磨损率越低；当冲击颗粒粒径小于200μm时，磨损率随着粒径的增大而增大，当粒径超过200μm，磨损率几乎不再变化。d）对原煤液化管道提出了一种优化改进方案，经计算模拟有望使管道最大磨损率减小1/2。本文研究对现役管道系统进行在役检验布点及结构优化有参考意义，且具有一定的工程应用前景。

［1］刘鸿亮，曹凤中.煤化工产业的发展与环境资源约束［C］.中国化工学会煤化工专业委员会.2008中国煤炭加工与综合利用技术、市场、产业化发展战略研讨会论文集，2008：158-161.

［2］Li J，Yang J L，Liu Z Y.Hydrogenation of heavy liquids from a direct coal liquefaction residue for improved oil yield［J］.Fuel Processing Technology，2009，90（4）：490-495.

［3］Peter N，Alan S，Rui H C.Coal liquefaction，Shenhua Group，and China's energy security［J］.European Management Journal，2004，22（2）：150-164.

［4］董刚，张九渊.固体粒子冲蚀磨损研究进展［J］.材料科学与工程学报，2003，21（2）：307-312.

［5］Wang ZC，Shui H F，Gu X P.Study on the hydrothermal treatment of shenhua coal［J］.Fuel，2008，87（4）：527-533.

［6］Chen X H，Brenton S M，Siamack A S.Application and experimental validation of a computational fluid dynamics（CFD）-based erosion prediction model in elbows and plugged tees［J］.Computers&Fluids，2004，33：1251-1272.

［7］Forder A，Thew M，Harrison D.A numerical investigation of solid particle erosion experienced within oilfield control valves［J］.Wear，1998，216：184-193.

［8］Fluent Inc.Fluent 6.0 User's Guide.［M］.Lebanon：New Hampshire，USA，2001.

［9］Levy A，Chik P.The effects of erodent composition and shape on the erosion of steel［J］.Wear，1983，89：151-162.

［10］Chacon N J G，Martinez V A，Almeraya C F，et al. Some remarks on particle size effects on the abrasion of a range of Fe based alloys［J］.Tribology International，2010，43：1307-1317.

Prediction and Analysis of Erosion Wear Distribution in Multiphase Flow Pipeline with Coal Liquefaction

OU Guo-fu，GONGBao-long，LI Wei-zheng，Bao Jin-zhe，JIN Hao-zhe
（Institute of Flow Induced Corrosion，Zhejiang Sci-Tech University，Hangzhou 310018，China）

In allusion to the problem of erosion wear of multiphase flow pipe system in coal chemical industry，this paper uses Fluent software to establish fluid dynamics model and obtains the relationship between wear rate and pipeline position for predicting the main area where wear reduces.The result of numerical calculation shows that，with the increase of pipe diameter，its maximum wear rate reduces；when the radius of curvature is three times of nominal diameter，the wear rate of elbow is low and uniform；when the particle shape is closer to sphere，wear rate is lower；when the size of wear particle is less than 200μm，wear rate increases with the increase of particle size；when the particle size exceeds 200μm，wear rate hardly changes.This paper transforms the design of the original pipe system and puts forward a structural optimization improvement program.The computational simulation result shows that the optimization program can make its wear rate decrease by 1/2 of the original one.

coal chemical industry；multiphase flow pipeline；erosion wear；failure analysis

TQ0558；TH117.1

A

（责任编辑：张祖尧）

1673-3851（2014）03-0247-05

2013-09-22

国家自然科学基金项目（U1261124）；国家科技支撑计划（2012BAK13B03-02）；浙江理工大学研究生创新研究项目（YCX12027）

偶国富（1965-），男，江苏太仓人，博士，教授，主要从事流动腐蚀预测及特种装备安全保障技术研究。

金浩哲，电子邮箱：haozhe2007@163.com