一类非线性抛物型方程反问题的中心差分正则化算法

张海丽，葛美宝，徐定华

（1.同济大学浙江学院，浙江嘉兴314000；2.浙江理工大学，a.科学与艺术学院；b.理学院，杭州310018）

一类非线性抛物型方程反问题的中心差分正则化算法

张海丽1，葛美宝2a，徐定华2b

（1.同济大学浙江学院，浙江嘉兴314000；2.浙江理工大学，a.科学与艺术学院；b.理学院，杭州310018）

大量线性与非线性抛物型方程反问题以各种不同形式出现在不同应用背景下，这类方程的研究有重要的应用价值，但是非线性抛物型方程反问题存在不适定性，文中利用半中心差分法思想设计了稳定的数值算法求解反问题，研究了一类半线性抛物型方程逆时反问题的数值算法并进行数值模拟。数值模拟结果与精确解相吻合，说明了算法的有效性。

非线性抛物型；反问题；半中心差分；数值模拟；爆破时间

0 引 言

本文研究非线性抛物型方程的混合问题：

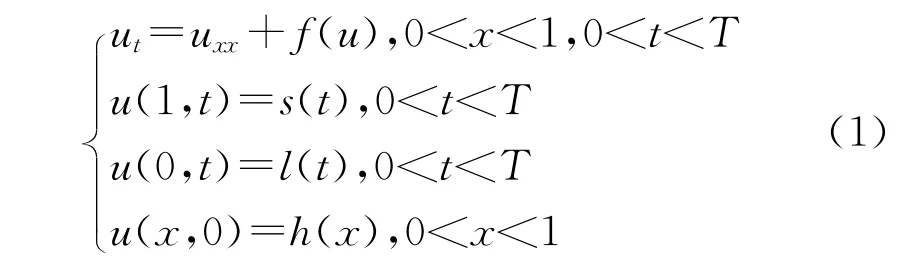
若给定源项f（·）、边界条件和初始条件s（t），l（t），h（x），定解问题（1）的求解称为正问题。根据抛物方程理论，在适当条件下，上述问题的解存在且唯一。若已知测量数据g（x）≡u（x，T）｜x∈［0，1］决定u（x，t），0＜x＜1，0≤t＜T的值，该问题称为逆时反问题。这类反问题有着非常重要的应用价值，引起了国内外反问题研究者的广泛关注和研究［1-7］。文献［4］利用中心差分法求解了一类含有源项的热传导方程的逆时反问题，结果表明数值解与精确解反演良好。本文利用文献［5］中提到的中心差分方法进行了数值模拟，模拟结果表明了该方法的有效性。对于上述问题，由于g（x）是有误差的观测数据，即使对于g（x）的微小误差也会引起解u（x，t）发生巨大变化。于是本文利用半中心差分正则化方法［5］的思想将此问题进行处理。

1 中心差分正则化方法

通过中心差分代替uxx，于是方程（2）近似变形为

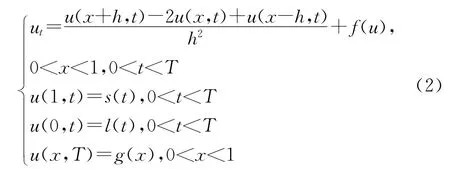
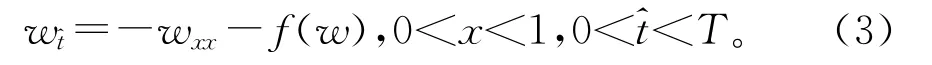
利用二阶中心差分，在xi处用差商的形式代替微分wxx，则（3）变形为

又由方程（2）中的边界条件可得出：

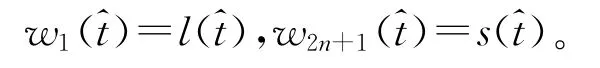
这时，方程（4）加上初始条件就会得到如下形式：

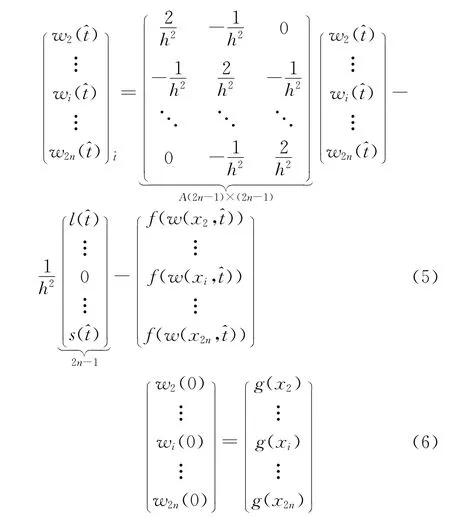
该问题是个带有初始条件的非线性的常微分方程组，通常情况可利用龙格库塔方法进行数值求解。但是根据三对角矩阵特征值的计算公式可知，上面矩阵A的特征值为（正整数集）。于是可知方程（5）的数值求解方法是不稳定的。故作变换：

其中a＞0为压缩因子。公式（4）变成为如下形式

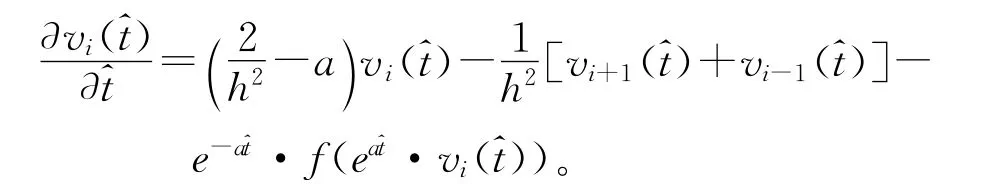
类似可得

2 数值模拟

2.1 正问题的模拟

考虑下面的正问题：

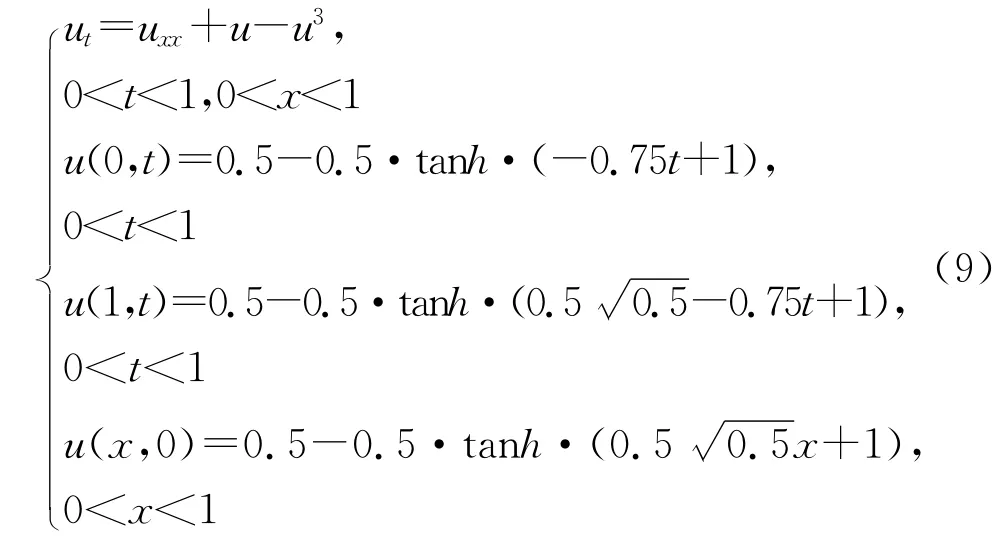
令x1=0，xi=（i-1）h，i=2，…2n，x2n+1=0，，其中，空间步长h=，时间步长τ=。经过剖分离散，这时显式的差分格式为：当满足步长比，该差分显格式具有稳定性。先将空间与时间经过剖分，获得网格m=101

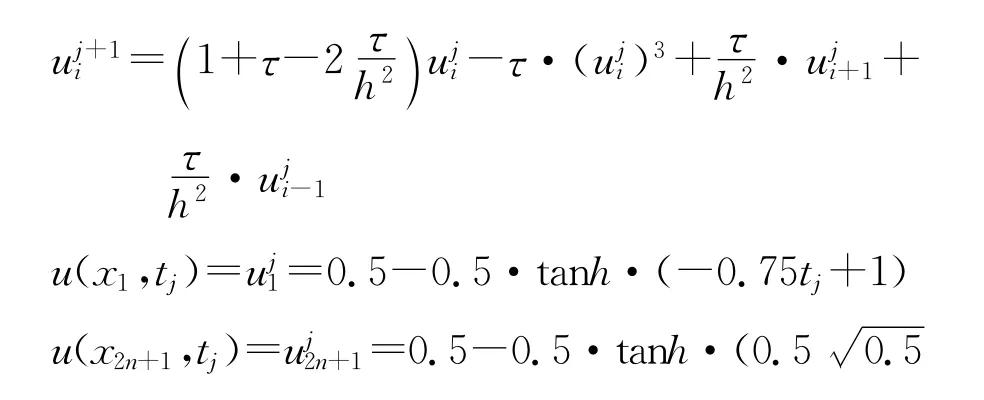
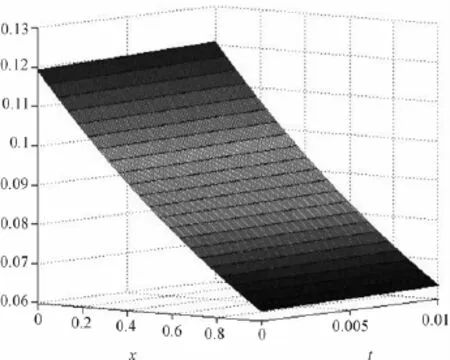
图1 正问题的精确解

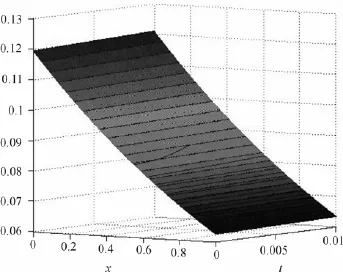
图2 正问题的数值解

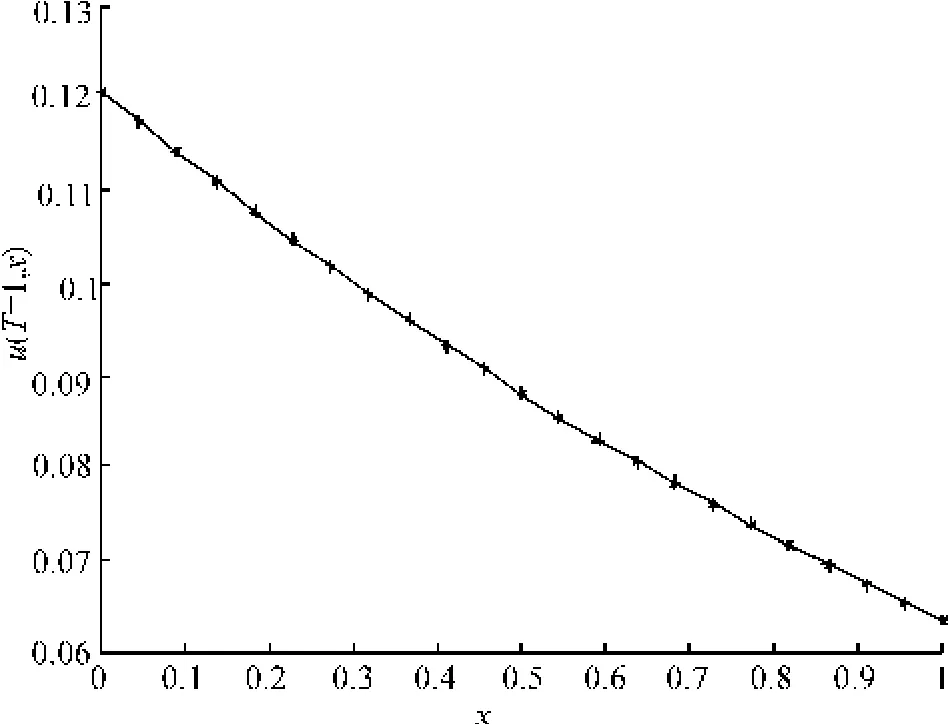
图3 T=0.01的精确解与数值解

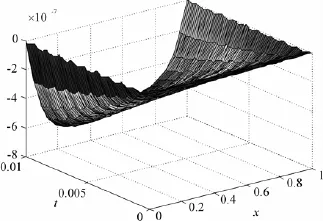
图4 精确解与数值解的误差

2.2 逆时反问题的模拟

通过中心差分正则化方法可进行逆时的反演，并结合上面算例正问题的模拟结果进行比较。采用终值时刻去反演初始时刻，即由u（x，T）的测量数据去反演u（x，0）时刻的值。

仍采用以上剖分，选择空间步长h=0.1和m=100。发现取b=4.6算法结果相对比较好，这也与矩阵稳定性的分析结果相吻合。数值模拟结果如图5和图6所示（实线代表精确解，星线代表数值解）。行、n=11列数据。此时正问题的精确解与数值解如图1和2。

选择时间的最后一行的数据，即g（x）=u（x，T=0.01）时的精确解和数值解进行比较，发现数值解与精确解之间的误差很小。模拟结果如图3和4所示（实线代表精确解，星线代表数值解）。

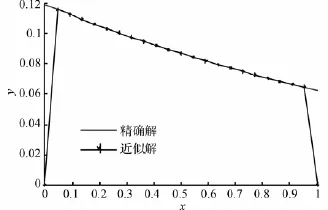
图5 精确解与数值解

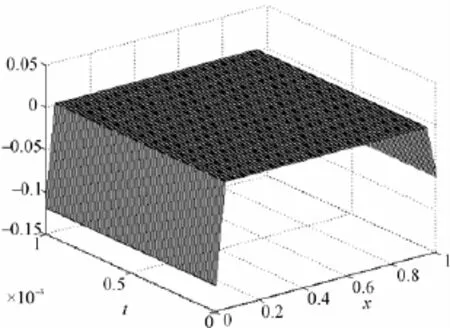
图6 精确解与反演解的绝对误差（T=0.001的情形）

如果分别取n=11和m=50，发现取b=2结果比较好，见图7和图8中的数值解与精确解非常吻合。

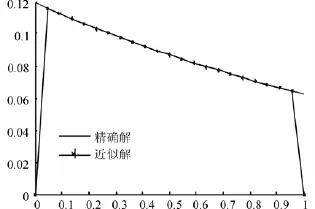
图7 精确解与数值解

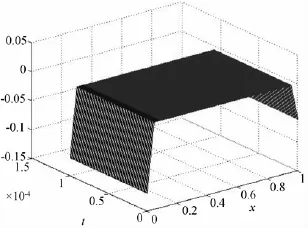
图8 精确解与数值解的绝对误差（T=0.000 1的情形）

3 结 论

本文利用了半中心差分的正则化方法对一维半线性抛物型方程的反问题进行了数值模拟，结果验证了该算法的有效性。算例中终值时刻T取值较小，这与正问题的解爆破时间有关系，这是由于随着时间增加，方程解发生了爆破，结果见图9-图12。故终值时刻T的取值不宜太大，否则会发生爆破。这也正是在实际计算中要求合理地选择探测数据获取时间的原因（取样时刻T）。

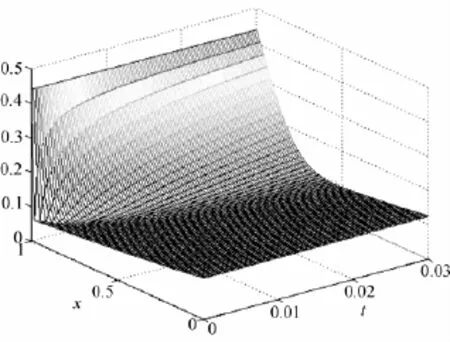
图9 T=0.03时刻的温度分布

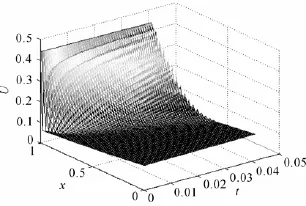
图10 T=0.04时刻的温度分布

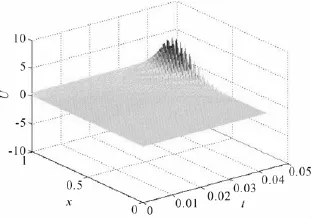
图11 T=0.042时刻的温度分布

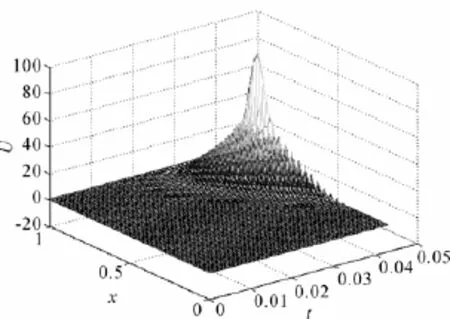
图12 T=0.042 7时刻的温度分布

本文空间步长选取非常关键，它起到正则化参数的作用。同时参数b的选取也是很重要的，它对数值结果的稳定性有影响。关于此算法的理论证明和分析，下一步将继续进行研究。

［1］Hoang Q P，Duc T D.A nonlinearly backward heat problem：uniqueness，regularization and error estimate［J］.Applicable Analysis，2006，85（6-7）：641-657.

［2］Jarny Y，Ozisik M N，Bardon J P.A general optimization method using adjoint equation for solving multidimensional inverse heat conduction［J］.International Journal of Heat and Mass Transfer，1991，34（11）：2911-2919.

［3］Marbán J M，Palencia C.A new numerical method for backward parabolic problems in the maximum-norm setting［J］.SIAM Journal on Numerical Analysis，2002， 40（4）：1405-1420.

［4］葛美宝，徐定华.一类热传导方程逆时反问题的数值解法［J］.浙江师范大学学报，2011，34（1）：59-63.

［5］Xiong X T，Fu C L，Qian Z.Two numerical methods for solving a backward heat conduction problem［J］. Applied Mathematics and Computation，2006，179（1）：370-377.

［6］曾苏华，徐定华.一类非线性抛物型方程扩散系数及初始分布同时反演的变分伴随方法［J］.江西科学，2007，25（5）：598-602.

［7］Xu D H，Zhang H L.Uniqueness and stability estimates for a semilinearly parabolic backward problem，boundary value problems，integral equations and related problems［C］//Singapore：Proceedings of the 3rd International Conference，2011：140-153.

［8］Shidfar A，Fakhraie M，Pourgholi R，et al.A numerical solution technique for a one-dimensional inverse nonlinear parabolic problem［J］.Applied Mathematics and Computation，2007，184（2）：308-315.

Central Difference Regularization Algorithm for a Kind of lnverse Problems of Nonlinear Parabolic Equations

ZHANG Hai-li1，GE Mei-bao2a，XU Ding-hua2b
（1.Tongji Zhejiang College，Jiaxing 314000，China；2.Zhejiang Sci-Tech University，a.School of Science and Art；b.School of Sciences，Hangzhou 310018，China）

A large number of inverse problems of linear and nonlinear parabolic equations occur in different application contexts in various forms.It is extremely important to study on these equations，but inverse problems of nonlinear parabolic equations are ill-posed.This paper uses semi-discrete central difference method to design a stable numerical algorithm to solve inverse problems，studies a kind of numerical algorithm to solve inverse problems of semi-linear parabolic equations，and conducts numerical simulation. Results of numerical simulation are consistent with exact solutions，indicating that this algorithm is effective.

nonlinear parabolic；inverse problems；semi-discrete central difference；numerical simulation；blow up time

O175.26

A

（责任编辑：李启正）

1673-3851（2014）03-0320-05

2012-12-19

国家自然科学基金（NSFC11071221、NSFC10561001）；浙江理工大学科研基金（KY2012015）

张海丽（1982-），女，河北张家口人，助教，硕士，从事数学物理方程反问题的研究。