基于改进量子进化算法的作业车间调度研究

张建明

（浙江理工大学理学院，310018杭州）

基于改进量子进化算法的作业车间调度研究

张建明

（浙江理工大学理学院，310018杭州）

针对作业车间调度问题，以最大完工时间最小化为优化目标，提出了跳跃基因量子进化算法（JGQEA）。该算法在量子进化算法的基础上引入跳跃基因算子，同时采用动态调整量子旋转角策略以提高算法的搜索能力。通过仿真实验验证了算法的有效性，结果表明JGQEA优于QEA等几种进化算法。

作业车间调度；转换机制；量子进化；旋转角；跳跃算子

0 引 言

量子算法是以量子力学原理为基础，它最本质的特点是利用量子态的相干性和叠加性，以及量子比特之间的纠缠性，与经典算法最本质的区别在于量子并行性。因此，量子计算比经典计算在速度上会有指数级的提高。但基于量子力学原理的量子计算机还处于研制的初级阶段，因此，将量子计算与传统智能计算相结合的量子智能计算就运用而生。

1996年Narayanan和Moore提出了量子遗传算法（quantum genetic algorithm，QGA），并应用于解决TSP问题［1］，开创了量子智能计算研究的新方向。2000年，由Han等［2］将量子位和量子门的概念引入进化算法，并用组合优化问题验证了算法的有效性。2002年，Han等［3］在量子遗传算法的基础上，引入种群迁移机制，提出了量子衍生遗传算法（quantum inspired genetic algorithm，QIGA）。目前对QGA的改进方式主要包括算法结构、进化方式以及编码方法等，比如中国科技大学杨俊安等［4］提出了一种多宇宙并行量子遗传算法，属于算法结构的改进；西南交通大学的张葛祥等［5］提出的采用量子比特相位比较法更新量子门和自适应调整搜索网格策略，与西南交通大学的陈辉等［6］提出的混沌更新旋转门转角的量子遗传算法，都属于进化策略方面的改进；在编码方法上的改进有：清华大学王凌等［7］给出的基于二进制编码的混合量子遗传算法和基于实数编码的混合量子遗传算法，李士勇等［8-9］在求解连续优化问题时提出的基于实数编码和目标函数梯度信息的双链量子遗传算法，以及基于量子位Bloch球面的量子进化算法［10］等。最近，在利用QGA对生产调度问题的研究中，Gu等［11-12］引入了量子交叉、变异等操作，获得了不错的优化效果。以上各种量子智能算法都是传统智能算法与量子算法相结合的产物。而跳跃基因算子在遗传算法中的成功实践，使我们有理由相信，提供了基因在种群内的水平传递的跳跃基因，有可能在量子算法中有利于种群多样性的保持，从而提高算法的优化性能。因此，本文针对作业车间调度问题，以最大完工时间最小为优化目标，在量子遗传算法中引入跳跃基因算子，提出跳跃基因量子遗传算法，以提高算法的优化性能。

1 作业车间调度问题的描述及数学模型

Job-shop调度问题包括典型Job-shop调度和带并行机的Job-shop调度。Job-shop调度问题是先进制造与自动化及其他调度技术相关研究领域中的经典热点问题。

生产系统有n个工件需要在m台机器上加工，调度的任务是把工序分配给机器上某个时间段，调度的目标就是确定每个机器上工件的加工顺序和每个工件的开始加工时间，使得完成所有工件所需的时间Makespan最小（加工周期或其他指标达到最优）。典型Job-shop调度问题的数学模型描述为［13］：

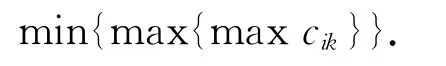
满足约束条件：

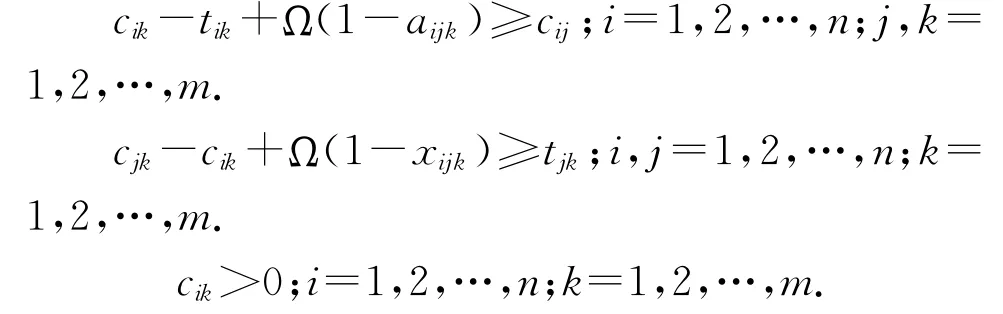
其中Ω是一足够大的正数，cik与tik分别表示第i个工件在第k台机器上的加工时间；aijk与xijk为：

2 基于作业车间调度问题的量子进化算法

本节在量子遗传算法的基础上，引入跳跃基因算子，以提高优良个体性能在种群进化过程中的有效传递；在量子个体更新的过程中，引进新的量子角的选择模式，以保持种群在进化过程中的多样性，防止早熟收敛。

2.1 编码机制

在量子进化算法中，一个量子比特位可以表示为

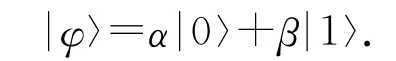
其中α，β为复数，且满足归一化条件｜α｜2+｜β｜2=1。一个具有l位的量子个体就表示为：

2.2 解码机制

对于车间调度问题，我们的目的是在满足工艺约束等条件下，合理安排各个工件在每台机器上的加工次序，使得最大完工时间等性能指标达到最优。而量子个体是通过概率幅对解的一种线性叠加态，因此，要通过解码机制，把线性叠加态的解解码为十进制的解。笔者在文献［10］中解码方法的基础上，提出以下解码方案。

第四步，将D（t）中的数按从小到大排序，最小的m个数表示第一个工件，接下来的m个数表示第二个工件，依次类推。在此过程中保持每个数在D（t）中的相对位置不变。因此，可以得到n个工件序号每个都重复m次的一个排列S（t）。S（t）中的第k次出现的数i将表示第i个工件的第k道工序。如果在D（t）中出现相等的数字，则位置序号较小的数代表工序号较小的工件。

解码流程图如图1所示。

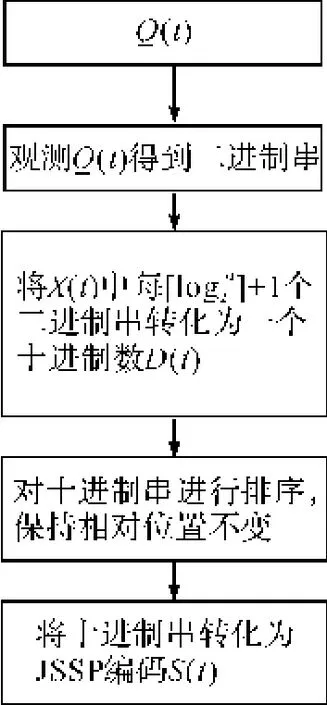
图1 编码及解码过程

以3个工件2台机器的3×2JSSP调度问题为例：则Q（t）为12位量子比特位的染色体，对Q（t）进行观测，若得到的12位二进制串X（t）=｛0，1，1，1，0，1，0，1，0，0，1，1｝，则D（t）=（1，2，1，1，0，2），因此，位置1与位置5表示工件1；位置3与位置4表示工件2；位置2与位置6表示工件3。因此，S（t）=（1，3，2，2，1，3），则位置1中的1表示第一个工件的第一道工序，位置5中的1表示第一个工件的第二道工序；位置3中的2表示第二个工件的第一道工序，依次类推。所以，任何一个量子个体都可以解码为一个可行调度，该方法的优点是解码方法简单，同时不会产生非法解。

2.3 量子旋转角

在QEA中，利用量子门进行量子个体的更新，而量子旋转门是被广泛采用的更新手段。在此过程中，量子旋转角的选择将起到至关重要的作用。对于旋转角，不仅要确定旋转角的大小还要确定旋转角的方向。旋转角θ和旋转方向可以通过表1得到，其中ri为当前量子个体第i个量子比特位所观测到的二进制编码（0或1）；bi为当前最优个体的第i位量子比特位所观测到的二进制编码；Δθi为旋转角的大小，控制算法收敛的速度；s（αi，βi）为旋转角的方向，保证算法的收敛；f（x）为适应度函数。比如，当ri=0，bi=1，f（r）＞f（b）时，为使当前解收敛到一个具有更高适应度的量子个体，应增大当前解取得0概率，即要使得｜αi｜2变大，此时，如果（αi，βi）在第一、三象限，θ应顺时针方向旋转；如果（αi，βi）在第二、四象限，θ应逆时针方向旋转，以增大｜αi｜2的值。因此，旋转角大小的选择对算法的收敛性能具有巨大的影响。在大部分量子进化算法或混合量子进化算法中，量子旋转角的大小总是通过查表给出，量子旋转角的大小往往是固定的。大小的选择通常也是根据具体问题由经验给出，与目标函数的本身没有太大的关系。尽管量子进化算法中个体的表示方式决定了量子种群比经典的进化算具有更强的多样性，但量子个体进化过程中αi逐渐向0或1收敛而使种群失去多样性。为了保持种群的多样性，使得进化更具有目的性，本文采用动态调整旋转角策略。在进化初期由于为了使每个解都有被搜索到的可能，旋转角θ应小一些，以提高种群的探索能力；在进化中期种群会逐渐失去多样性，因此应增大旋转角θ；在进化后期为了提高种群的开发能力，增加种群的局部搜索能力，应再次减小旋转角θ。因此，笔者采用第一代到（T为最大进化代数）代内旋转角线性增加；在代之后旋转角线性减少。即：

表1 量子旋转角

2.4 跳跃基因算子

目前，跳跃基因算子主要有两种形式：剪切粘贴置换与复制粘贴置换［14］。这两种置换又分为在同一染色体内的置换与染色体之间的置换。同一染色体内的剪切粘贴置换就是在染色体内随机产生一个剪切点和随机长度的跳跃基因，再随机产生一个新的粘贴点，将跳跃基因粘贴到新的粘贴点上，如图2（a）。染色体间的剪切粘贴置换是在两个不同的染色体上都随机产生一个剪切点和随机长度的跳跃基因，同时在每个染色体上随机产生一个新的粘贴点，然后将两个跳跃基因片段交叉粘贴到新的粘贴点处。染色体内的复制粘贴置换就是在染色体内随机产生一个复制点和随机长度的跳跃基因，再随机产生一个新的粘贴点，将跳跃基因复制到新的粘贴点上，如图2（b）。在染色体间的复制粘贴置换是在两个不同的染色体上都随机产生一个复制点和随机长度的跳跃基因，同时在每个染色体上随机产生一个新的粘贴点，然后将两个跳跃基因片段交叉复制到新的粘贴点处。本文采用在同一染色体内的剪切粘贴置换，并把这种引入跳跃基因算子的量子遗传算法称为跳跃基因量子进化算法（jumping genes quantum evolutionary algorithm，JGQEA）。

图2 同一染色体内的置换

针对JSSP的JGEQA伪代码为：

3 仿真结果与分析

为了验证JGQEA对JSSP的有效性，选取Muth与Thompson提出的经典的基准问题mt06、mt10及mt20［15-16］和由Applegate与Cook提出的经典的基准问题la01、la02、la03、la04、la05、la06、la21、la24、la33、la36及la38，与MA、GA、SGA、PSO及 QEA的优化效果进行比较。表2中JGQEA的测试参数为：种群规模为300，跳跃概率为0.1，最大代数为300。利用Matlab编程，测试环境为：Intel（R）Core 2 Duo 2.93GHz CPU，2G内存。表中OPT表示最优解，MA表示基因算法（memetic algorithm）［17］，GA表示遗传算法（genetic algorithm）［18］，SGA表示Nakan与Yamada提出的遗传算法［19］，PSO表示离子群算法（particle swarm optimization）［20-21］，QEA表示普通量子进化算法。从表2可知，尽管JGQEA不是所有问题中都得到最优解，但所得到的最优解好于GA、SGA、PSO、QEA等方法获得的最优解，在mt10、mt20、La38中所获的最优解较MA算法获得的最优解差。由此可以说明，JGQEA有较好的优化性能。在QEA与JGQEA的比较中可以发现，引入跳跃基因算子的JGQEA的优化性能比QEA都有所提高，这进一步说明跳跃基因算子可以改善算法的优化性能。为了比较不同的跳跃概率对算法收敛速度的影响，笔者以La06为例，选择不同的跳跃概论来比较它们的收敛速度，如图3所示。

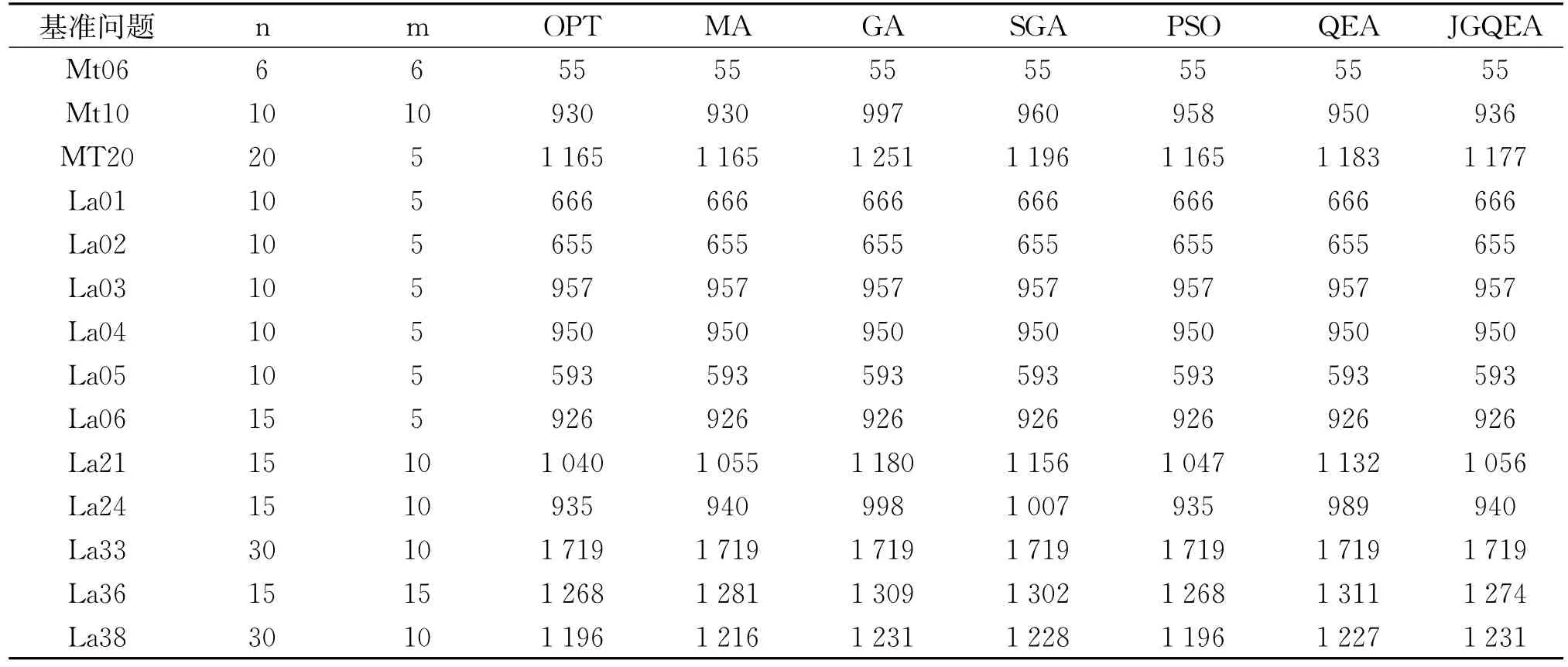
表2 最优结果比较

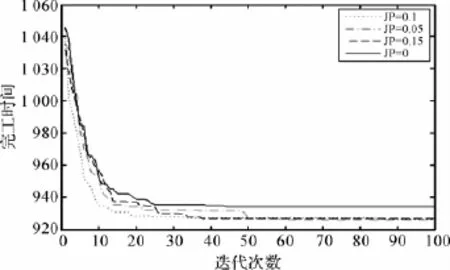
图3 不同跳跃概率下收敛速度比较（La06）

图4 对La06不同算法的比较

图3中，我们取A=0.03，C=0.01；种群规模为300，最大代数100，运行次数为10次；跳跃概率分别取0、0.05、0.1、0.15；竖轴表示运行10次完工时间的平均值，横轴表示运行代数。从图中可以看出，当选择一个恰当的跳跃概率时，算法的收敛速度会得到有效的改善，特别是在跳跃概率分别取0.05、0.1、0.15时，其收敛速度都优于跳跃概率为零的情况。在图4中，以La06为模拟对象，将JGQGA与POS、QGA、GA的优化性能做了比较，结果显示JGQGA比这几种算法在优化质量上都有所提高。其中JGQGA中相关参数为：种群规模300，最大代数150，A=0.03，C=0.01，跳跃概率为0.1。

4 结 论

本文提出了JGQEA用于解决JSSP问题。在JGQEA中采用动态调整量子旋转角的策略，同时引入跳跃基因，以改善量子种群的多样性，提高JGQEA的优化性能。对多个JSSP的基准问题以最大完工时间为优化目标进行优化调度，JGQEA所获地的最优值优于GA、SGA、PSO及QEA所获得的最优值，但是不及 MA所获得的最优值。这一方面说明，JGQEA具有良好的优化性能，另一方面也说明JGQEA的优化性能还有进一步改进和提高的要求。在优化目标方面，本文仅对最大完工时间作为优化目标对JGQEA的优化性能进行检验。实际的调度目标往往包括利润最大、库存最小、提前拖期惩罚最小等等的多目标调度，因此，如何将JGQEA用于JSSP的多目标调度具有非常重要的研究价值，这也是我们以后要重点研究的内容。

［1］Narayanan A，Moore M.Quantum inspired genetic algorithm［C］//IEEE International Conference on Evolutionary Computation.Iscataway，1996：61-66.

［2］Han K H，Kim J H.Genetic quantum algorithm and its application to combinatorial optimiza-tion problem［C］// IEEE International Conference on Evolutionary Computation.Lajolla，2000：1354-1360.

［3］Han K H，Kim J H.Quantum-inspired evolutionary algorithm for a class of combinatorial timization［J］.IEEE Transactions on Evolutionary Computation，2002，6（6）：580-593.

［4］杨俊安，庄镇泉，史 亮.多宇宙并行量子遗传算法［J］.电子学报，2004，32（6）：923-928.

［5］Zhang G，Gu Y，Hu L，et al.A novel quantum genetic algorithm and its application to digital filter design［J］.Intelligent Transportation Systems，2003，2：1600-1605.

［6］Chen H，Zhang J H，Zhang C.Chaos updating rotated gates quantum-inspired genetic algorithm proceedings of the international conference on communications［J］. Cuircuits and Systems，2004，2：1108-1112.

［7］Wang L，Tang F，Wu H.Hybrid genetic algorithm based on quantum computing for numerical optimization and parameter estimation［J］.Appl Math Comput，2005，171：1141-1156.

［8］Li P，Li S.Quantum-inspired evolutionary algorithm for continuous spaces optimization［J］.Chinese Journal of Electronics，2008，17（1）：80-84.

［9］李士勇，李盼池.基于实数编码和目标函数梯度的量子遗传算法［J］.哈尔滨工业大学学报，2006，38（8）：1216-1218，1223.

［10］Li P，Li S.Quantum-inspired evolutionary algorithm for continuous spaces optimization based on Bloch coordinates of qubits［J］.Neurocomputing，2008，72：581-591.

［11］Gu J，Gu X，Gu M.A novel parallel quantum genetic algorithm for stochastic job shop scheduling［J］.J Math Anal Appl，2009，355（1）：63-81.

［12］Gu J，Gu M，Cao C，et al.A novel competitive co-evolutionary quantum genetic algorithm for stochastic jobshop scheduling problem［J］.Comput Oper Res，2010，37（5）：927-937.

［13］张建明.基于改进量子进化算法的生产调度问题研究［D］.上海：华东理工大学，2013.

［14］Ripon K S N，Sam K，Man K F.A real coding jumping gene genetic algorithm（RJGGA）for multi-objective optimization［J］.Inf Sci，2007，177（2）：632-654.

［15］Muth J F，Thompson G L.Industrial Scheduling［M］. EngleWood Cliffs：Prentice-Hall，1963.

［16］Ripon K S N，Chi H T，Sam K.Multi-objective evolutionary job-shop scheduling using jumping genes genetic algorithm［C］//2006 International Joint Conference on Neural Networks.Vancouver，2006：3100-3107.

［17］Gao L，Zhang G，Zhang L，et al.An efficient memetic algorithm for solving the job shop scheduling problem［J］.Comput Indust Engin，2011，60：699-705.

［18］Ombuki B M，Ventresca M.Local search genetic algorithms for job shop scheduling problem［J］.Applied Intelligence，2004，21：99-109.

［19］Nakano R，Yamada T.Conventional genetic algorithm for job-shop problems［C］//Proceedings of the 4th International Conference on Genetic Algorithms（ICGA'91）.San Diego，1991：474-479.

［20］Kennedy J，Eberhart R C.Particle swarm optimization［C］//IEEE International Conference on Neural Networks，Perth，1995：1942-1948.

［21］Tasgetiren M F，Sevkli M，Liang Y C.A particle swarm optimization and differential evolution algorithms for job shop scheduling problem［J］.Inter J Oper Res，2006，3（2）：120-135.

A Novel Quantum Evolutionary Algorithm for Job-shop Scheduling

ZHANG Jian-ming
（School of Sciences，Zhejiang Sci-Tech University，Hangzhou 310018，China）

For job-shop scheduling，this paper proposes jumping gene quantum evolutionary algorithm（JGQEA）with the optimization objective of minimizing the makespan.This algorithm introduces jumping gene operator based on quantum evolutionary algorithm，and applies dynamic adjusting quantum rotation angle strategy to improve search capability of the algorithm.The effectiveness of the algorithm is verified by simulation experiment，and results show that JGQEA is superior to QEA and several other evolutionary algorithm.

job-shop scheduling；converting mechanism；quantum evolution；rotation angle；jumping operator

TP18

A

（责任编辑：康 锋）

1673-3851（2014）03-0310-06

2013-12-30

国家自然科学基金（10871181）

张建明（1972-），男，陕西延川人，博士、副教授，主要从事微分方程分支问题及智能计算方面的研究。