蒙特卡洛法在位标器公差分析中的应用

陈振中， 彭思平， 刘元云， 顾网平

（上海无线电设备研究所，上海 200090）

蒙特卡洛法在位标器公差分析中的应用

陈振中， 彭思平， 刘元云， 顾网平

（上海无线电设备研究所，上海 200090）

位标器作为导引头的关键组件，对整个制导系统精度的提升起着重要作用。以位标器的装配过程为研究对象，介绍了蒙特卡洛方法在装配公差分析中的应用；讨论了蒙特卡洛方法在位标器不同公差特性条件下的适应程度；为蒙特卡洛方法在位标器公差分析中的应用提供了技术指导，有效地保证了其在公差分析中的精度。

蒙特卡洛；位标器；公差分析

0 引言

位标器安装于制导系统的头部，它是制导系统的关键组件。位标器的用途包括：空间稳定、角位置预定、空间角扫描、目标角度跟踪等[1]，它的装配精度是制约导引头系统制导精度的关键。

位标器具有结构复杂，零部件较多的特点，因此在其装配过程中极易出现累计装配误差较大的情况。当封闭环装配间隙过大，则需要加装垫片；当封闭环装配过盈量较大，则需要对组成环零件进行修磨；为了使位标器达到较高的装配精度，要求装配人员必须进行反复修配，因而造成了大量人力物力的浪费。

因此，针对位标器的复杂装配结构，提出一套准确的公差分析技术，可以有效地控制位标器累计装配误差，提高位标器的装配效率，降低制造成本。

公差分析方法大致分为两类：极值法和概率法。极值法要求装配过程完全互换，该方法只考虑公差的极限上下偏差，因而对公差的分析过于保守。概率法包括方和根法、田口实验法、卷积法和蒙特卡洛法[2]，其中，蒙特卡洛方法最为精确。

本文将首先介绍蒙特卡洛公差分析方法的基本原理及其在应用过程中的特点，然后将蒙特卡洛方法应用于位标器公差分析的实例当中，并分别对不同公差特性的情况进行讨论，最后给出结论。

1 蒙特卡洛公差分析

1.1 蒙特卡洛思想

蒙特卡洛方法的思想：通过随机模拟某一不确定性事件，产生大量样本，然后对样本的响应值进行概率统计，进而获得该不确定事件的参数评价，如均值、方差、概率等[3]。

蒙特卡洛是以大数定律为依据，它的收敛性已经得到了证明。蒙特卡洛的应用范围非常广泛，如数学积分、物理过程模拟、风险评估等。以求解积分为例，可表示为

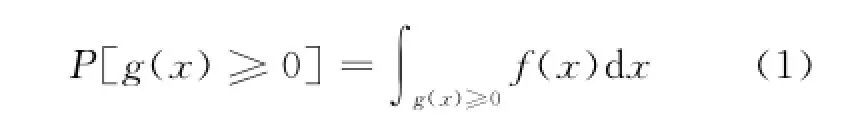
式中：f（x）为积分概率；g（x）≥0为积分区域。

采用蒙特卡洛模拟方法，可通过随机抽样进行求解，可表示为

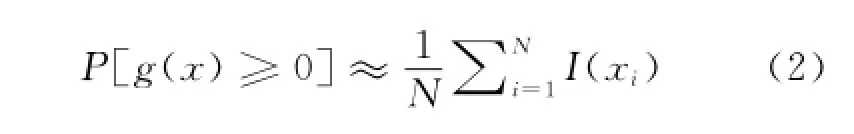
式中：xi为随机样本；N为随机抽样的数量；I（xi）为指示函数，具体计算如式（3）所示：

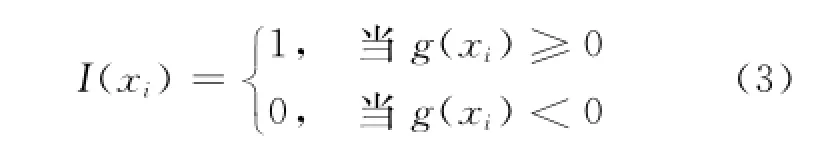
从式（2）中可以看出，蒙特卡洛方法需要进行大量的随机模拟，模拟的精度与样本数量N有直接的关系，所以蒙特卡洛方法的计算成本较高。然而，随着计算机技术的快速发展，蒙特卡洛方法的计算成本劣势逐渐淡化，而其高精度的求解效果逐渐受到重视。

1.2 蒙特卡洛公差分析方法

从上节内容可知，蒙特卡洛方法的核心思想即随机数的产生。在各种计算机编程语言中均有随机数或者伪随机数的生成方法，这些方法足以满足工程的需要，如VB中的Rnd（），Excel中的RAND（），Matlab中的rand（）。

通常在编程语言中，随机数发生器所产生的样本RU服从（0，1）区间上的均匀分布；而在公差分析中，零件的尺寸存在多种分布类型，因而需要将随机样本RU由均匀分布转换为其它类型的分布。标准正态分布RN的转换公式可表示为[4]

由均匀分布随机数RU转换为常见的分布类型随机数的方法如表1所示[5]，其中µ，σ，λ，a，b，c分别是不同分布类型的参数。

表1 常见随机分布类型转换公式

蒙特卡洛公差分析的流程如图1所示，具体步骤如下所示。

（1）确定各个组成环的尺寸和公差

包括公差的上下偏差、分布类型、中心偏移系数等，对于不同零部件的公差类型，可以根据测试或者历史数据进行评价。然而由于材料、尺寸、加工方式的不同，很难找到一种统一的评价方法，在实际操作中公差分布类型往往依据经验或假设进行选择。

（2）生成组成环尺寸的随机数

生成（0，1）上服从均匀分布的随机数，然后依据组成环的公差类型进行转换，常见的转换公式如表1所示。随机数可以逐个生成，如图1所示，直至达到抽样次数要求；也可以一次性生成，在Matlab中可以一次性生成106～107个样本，而且直接支持各种分布类型的随机数。

图1 蒙特卡洛公差分析方法流程

（3）分析计算封闭环尺寸均值和方差

求解公差分析函数，并对封闭环公差进行统计处理。

在蒙特卡洛方法中，封闭环样本的均值和标准差分别等于封闭环的均值和方差[6]，封闭环样本为Ai，i=1，…，N，则封闭环均值Aaυ求解方法：

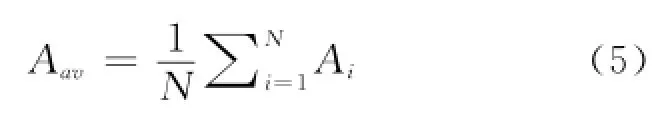
封闭环标准差σ求解方法为

封闭环公差带T求解方法，如式（7）所示。在公差分析中，公差带置信水平通常为99.73%，也即6σ区间。

封闭环尺寸上下偏差Amin，Amax的求解方法为

1.3 蒙特卡洛公差分析的几点讨论

蒙特卡洛方法通过大量随机抽样，可以实现封闭环尺寸的精确模拟。然而现有方法对所获得的封闭环模拟尺寸的统计处理过程存在一定的误差，从而造成了蒙特卡洛公差分析的结果缺乏精度，具体体现在以下几个方面：

（1）随机数设计空间的变化

随机数生成器通常建立在（0，1）区间均匀分布基础之上，然后再根据各组成环的分布类型进行转换，具体公式如表1所示。然而经过转换后，个别分布类型如正态分布的参数设计空间变为（-∝，＋∝），而实际的组成环尺寸必须位于公差带以内，即服从截尾分布。所以，必须将位于组成环公差带之外的随机样本去除。

（2）组成环公差中心偏移的影响

现有的方法通常以公差带、上下偏差以及分布类型等参数对组成环尺寸公差进行描述，并假定组成环的置信水平为99.73%。然而即便上述参数均为已知的情况下，依然不能确定组成环公差的具体分布参数。假设某服从正态分布的组成环公差中心为µA，则依据公差的置信水平99.73%可知

从式（9）可知，当组成环公差中心发生偏移时，组成环尺寸的标准差σA也将随之发生变化，因而在确定组成环分布参数时，必须考虑公差中心偏移量的影响。

（3）封闭环公差分布类型的选择及处理

当组成环尺寸都服从正态分布，且公差函数为线性时，封闭环尺寸也将服从正态分布，此时，封闭环的公差处理采用式（5）～式（8）是准确的；当组成环尺寸存在多种分布的情况，且组成环数量较多时，则封闭环近似服从正态分布。然而，现有的方法很难判断组成环数量是否足够多，更无法判断假设封闭环服从正态分布所带来的具体影响。因此，现有的方法对封闭环尺寸均采用正态分布，上下偏差采用3σ准则必然存在一定的误差。

2 位标器公差分析

位标器某装配尺寸链如图2所示，其中组成环为A1，A2，A3，A5，A6，A7，封闭环为A4。组成环尺寸及其公差如表2所示。

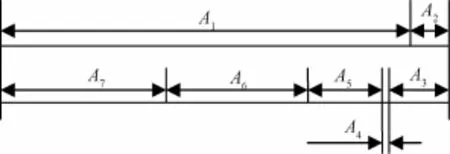
图2 位标器装配尺寸链

本文将分以下几种情况采用蒙特卡洛方法进行公差分析：

a）情况1：组成环尺寸均服从正态分布，且尺寸中心位于公差带中心无偏移；

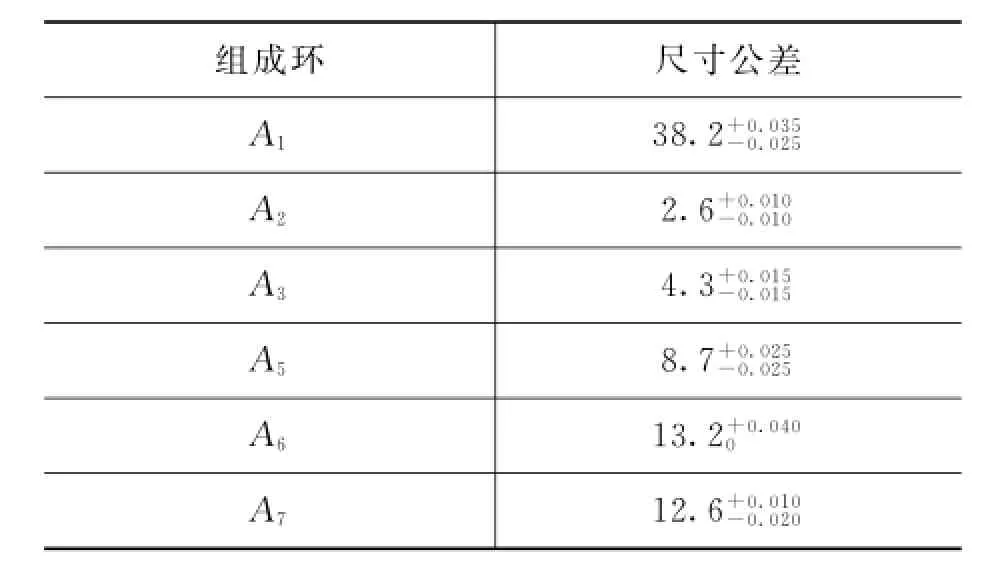
表2 位标器组成环尺寸及其公差

b）情况2：组成环尺寸均服从截尾正态分布（将公差带之外的随机样本进行过滤），且尺寸中心位于公差带中心无偏移，组成环置信水平为99.73%；

c）情况3：组成环尺寸均服从正态分布，且尺寸中心存在偏移：µA1=38.206，µA2=2.601，µA3=4.301，µA5=8.706，µA6=13.221，µA7=12.596；

d）情况4：组成环尺寸均服从均匀分布，且均匀分布上下界分别为公差带的上下偏差；

e）情况5：组成环尺寸A1，A2，A7服从截尾正态分布，置信水平为99.73%，且中心偏移：µA1=38.206，µA2=2.601，µA7=12.596；A3，A5，A6服从均匀分布，且均匀分布上下界分别为公差带的上下偏差。

本文采用Matlab软件进行仿真模拟，每种情况的抽样次数均为109，公差分析结果如表3所示。采用极值法在以上五种情况中得到的结果完全一样，而且过于保守；蒙特卡洛方法所获得结果差异较大，其中，“样本极限值”表示封闭环尺寸在所有样本中出现的最大最小值。

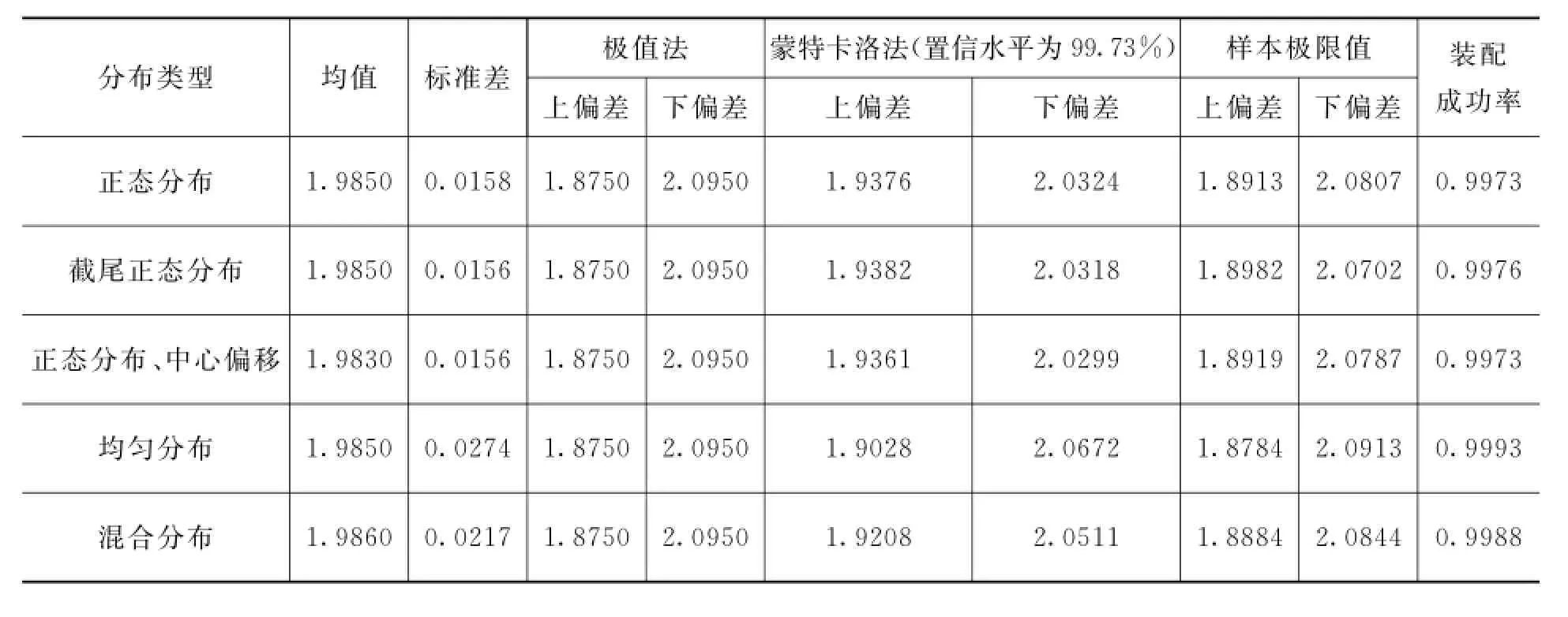
表3 位标器封闭环公差分析结果对比

“装配成功率”定义：在蒙特卡洛法抽取的所有封闭环样本中，位于公差带内的样本出现的频次。本文中蒙特卡洛方法与现有方法保持一致，即假定封闭环尺寸服从正态分布，且公差带置信水平为99.73%，因而“装配成功率”越接近“99.73%”，则表示蒙特卡洛方法越精确。

从表3中可以看出，第一种情况，组成环尺寸均服从正态分布，它的“装配成功率”为99.73%。因而对于该种情况，蒙特卡洛方法假设封闭环尺寸服从正态分布是准确的，如图3所示，封闭环尺寸的随机样本频次分布图与正态分布完全一致。

第二种情况组成环为截尾正态分布。它的标准差为0.0156，比第一种情况的标准差略微减小，公差带也有所缩减；“装配成功率”为99.76%，较正态分布有所提高。因此，当组成环尺寸服从截尾正态分布，则封闭环尺寸的公差带将有所缩减，且该公差带的选取具有保守倾向。如图4所示，封闭环尺寸的随机样本频次分布图与正态分布基本一致。

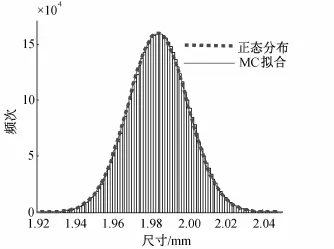
图3 组成环为正态分布

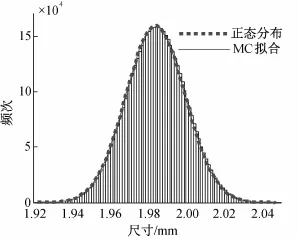
图4 组成环为截尾正态分布

第三种情况组成环尺寸服从正态分布，且尺寸中心具有一定的偏移量。从表3中可以看出，封闭环尺寸均值为1.9830，较第一、二种情况有所偏移，标准差0.156，较第一种情况略微减小，公差带为[2.0299，1.9361]，有明显的缩小。该种情况变化的原因是尺寸中心偏移后，尺寸标准差将减小，具体可由式（9）进行计算。然而，尺寸中心偏移并不影响“装配成功率”，且封闭环尺寸服从正态分布，如图5所示，封闭环尺寸的随机样本频次分布图与正态分布完全一致。

第四、五种情况，组成环尺寸分别为均匀分布和混合分布。从表3中可知，该两种情况封闭环的标准差明显增大，公差带范围随之增大，装配成功率也明显大于目标值99.73%，从图6、7中可以看出，封闭环尺寸的随机样本频次分布图相对于正态分布有明显的变矮变胖的趋势。因此，针对该两种情况，采用蒙特卡洛方法所计算的结果过于保守。

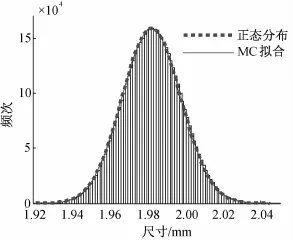
图5 组成环为正态分布、且中心偏移

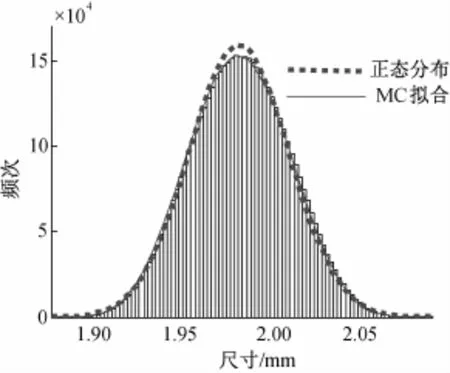
图6 组成环为均匀分布

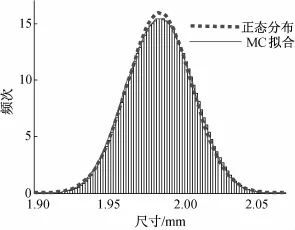
图7 组成环为混合分布

3 结论

本文以位标器装配公差为研究对象，介绍了蒙特卡洛方法在公差分析中的一般步骤，并探讨了蒙特卡洛方法在五种不同情况下的适应程度。

蒙特卡洛方法中，组成环尺寸样本如果按照无限区域的分布类型进行抽样，将与生产实际不相符；然而如果按照截尾分布类型进行抽样，则封闭环尺寸将不完全服从正态分布的假设。当组成环尺寸的分布类型具有多样化的情况，且组成环的个数不足够大时，封闭环尺寸公差的选取将会出现保守的趋势。以上这些情况，在位标器装配分析过程中，应该给与充分考虑，避免公差设计过于保守而引起制造成本的浪费。

[1] 杨晓东，马伯渊.雷达导引头位标器的滑模控制方法研究[D].成都：电子科技大学，2010.

[2] 王平，沈晓阳.公差分析中的统计公差方法综述[J].工具技术，2008，4（10）：43-47.

[3] Chen Zhen-zhong，Qiu Hao-bo，Gao Liang，et al. A Local Adaptive Sampling Method for Reliability-Based Design Optimization Using Kriging Model [J].Structural and Multidisciplinary Optimization，2014，49：401-416.

[4] 袁贵星，王平.蒙特卡洛模拟及其在公差设计中的应用[J].天津科技大学学报，2008，32（2）：60-64.

[5] 庞晓红.基于Excel的蒙特卡洛法及其在工程设计上的应用[J].漳州职业技术学院学报，2006，8（3）：20-23.

[6] 董银月，邱浩波，蒋平.基于蒙特卡洛方法和改进PSO算法的装配公差优化设计[D].武汉：华中科技大学，2011.

Monte Carlo Simulation and its Application in Position Marker Tolerance Analysis

CHEN Zhen-zhong， PENG Si-ping， LIU Yuan-yun， GU Wang-ping
（Shanghai Radio Equipment Research Institute，Shanghai 200090，China）

Position marker is an important component of the seeker；it has a critical impact on the accuracy of the guidance system.Focuses on the assembling process of the coordinator，introduces the application of the Monte Carlo simulation（MCS）method in assembling tolerance analysis and discusses the application of the MCS in several different tolerance conditions.This paper gives the guidance of the using MCSin coordinator tolerance analysis to avoid unnecessary error.

Monte Carlo；position marker；tolerance analysis

TJ765.232

A

1671-0576（2014）03-0055-06

2013-12-05

国家自然科学基金资助项目，编号51405302。

陈振中（1986-），男，博士，工程师，主要从事机械装配工艺与可靠性工作。