基于粗糙集－AHM的装备制造业企业创新能力评价指标权重计算研究

张晓明

(中国科学院大学，北京 100190)

一、引言

制造业是国民经济发展和国防建设的物质基础，是实现工业化和现代化的不竭动力，是增强国家综合实力的重要保障。一国是否具有高度发达的制造业体系，尤其是其机电工业是否发达已经成为衡量一个国家综合国力的重要标志。进入21世纪，随着科技进步的加速和竞争的加剧，创新对制造业竞争力的作用越来越明显，甚至起决定作用。提高我国制造业创新能力，是提高其国际竞争力的必由之路［1］。要实现我国从制造大国向制造强国的转变，必须通过制造业的创新，制造业的创新是我国制造业发展的根本［2］。高度关注制造业的技术创新现状，并努力提高其技术创新能力，这就首先要对装备制造业的创新能力进行科学、准确的评价。由于创新能力是一个综合性概念，很难用某个单项指标来衡量。国内外的学者对装备制造业企业的创新能力评价指标系统的研究，从不同的创新视角提出多种指标集［3-7］。在评价指标的研究上，目前主要有两种方法，一种是专家主观经验法，即通过专家问卷的方法为各指标进行打分确定;另一种方法是根据已有的样本数据，通过样本数据中抽取知识，获得各指标在评价中的重要性，从而确定指标的权重。指标权重是创新评价中的一个重点和难点。权重是指标本身属性的客观反映，其大小反映了综合评判中各参评因素的相对重要程度，其取值好坏直接影响到评价结果的可靠性和正确性。主观常用的权重计算方法主要有 AHP［8］、模糊统计［9］、二元对比排序［10］、多元回归［11］等。采用主观权重计算方法的主观随性大，容易受专家经验、知识的影响，常不能客观地反映实际情况［12-13］。一些学者提出基于客观数据的权重计算方法，如粗糙集［14］、均方差法［15］、因子分析法［16］、熵值法［17］等，虽然这些方面在一定程度上克服了受专家主观因素的影响，但却也容易受样本数据的选择影响，特别是当样本数据不够全面的情况，所获得的权重将严重偏离现实［18-19］。因此，本文提出一种基于粗糙集－AHM的企业创新能力评价指标确定的综合计算方法。该方法一方面利用粗糙集理论在处理不确定、不精确数据的优势，以及不需要先验信息，能够获得较为客观的指标权重信息;另一方面利用AHM又能够充分利用领域专家的经验、知识，获得专家对指标客观的重要性评价结果，克服AHP在评价时对一致性检验要求较高的不足。同时，文中构建一个线性加权函数对主、客观的指标权值进行综合，从而得到最后的评价指标权重。本文提出的基于粗糙集与AHM的装备制造业企业创新能力评价指标计算方法，也可以广泛应用于其它的评估中。

二、相关基础理论

(一)基于粗糙集理论的客观权重计算方法

粗糙集(Rough Sets)，理论是由波兰数学家Pawlak［20］于1982年提出的一种刻画不完整性和不确定性的数据分析工具，能够有效地分析和处理不精确、不一致和不完整的各种不完备信息，并从中发现隐含的知识，揭示潜在的规律［21-22］。

设信息系统S={U，A，V，f}，其中 U 为对象组成的有限集合，称为论域;A为属性的有限集合，A=C∪D，C为条件属性集，D为决策属性集;V=Ua∈AVa，Va是属性 a的值域;f:U ×A→V是总函数，使得 f(xi，a)∈Va，对于每个 a∈A，xi∈U。

在信息系统 S={U，A，V，f}中，设 P⊆A 为知识(即属性集)，且 P⊂Q，xi，xj∈U，定义二元关系IND(p)称为不可分辨关系，表示如下:

称xi和xj在S中关于属性集P是不可分辨的，当且仅当p(xi)=p(xj)对所有的p∈P成立，即xi和xj不能用p中的属性加以区别。

设X⊂U是个体全域上的子集，P⊆A，则X是关于P的下近似集，上近似集及边界区域分别为:

其中，U/P为U关于IND(p)的等价类。

在两个属性值C与D之间的依赖程度r(C，D)，可以定义

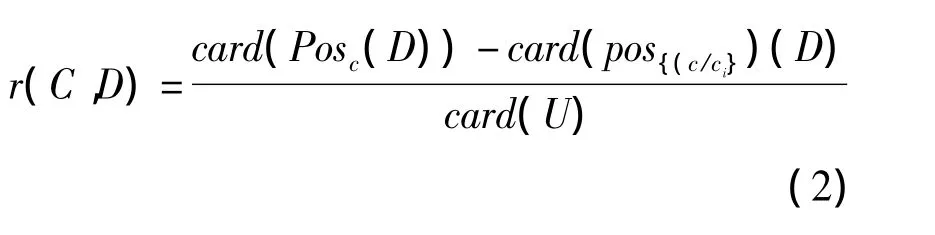
其中，card(U)表示集合U中元素的数量;POS{C/ci}(D)称为D的相对于{C/ci}的正区域，即U中所有属性根据{C/ci}进行划分后，仍可以准确地划分到D的等价类中的对象集合;card(POS{C/ci})(D)表示集合POS{C/ci}(D)中元素的个数。r(C，D)的值越大，则其对应的指标权重越大，反之越小。

(二)基于AHM的主观指标计算方法

层次分析模型AHM(Analytic Hierarchical Model)是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。它的特点是把复杂问题中的各种因素通过划分为相互联系的有序层次，使之条理化，根据对一定客观现实的主观判断结构(主要是两两比较)把专家意见和分析者的客观判断结果直接而有效地结合起来，且对判断矩阵的一致性要求很低，只要甲比乙强、乙比丙强，则甲比丙强，至于强多少没有具体要求。AHM与AHP方法较大的相似之处，但AHP对判断矩阵的一致性要求高，特别是当同层指标较多时，AHM的优势更为明显。在计算AHM中的比较判断矩阵μ=(μij)时，通常由AHP中的比较判断矩阵A=(aij)中导出［23-24］。

(三)评价指标综合权重计算函数构建

利用粗糙集与AHM方法可分别获得客观、主观两个方面的指标权重值，需要对其进行综合，以获得最后指标权重值，得到一组最终的评价指标权重。在本文的研究中，构建一个线性的加权函数计算评价指标的综合权重，如式(3)所示。

其中，wAi是指标客观权重值，wBi为指标主观权重值，u的取值根据具体情况而定，当决策倾向专家经验时，u∈［0，0.5］，而当决策倾向客观数据时，u∈［0.5，1］。最后计算所得到的 W权重，即为由主、客观权重综合计算所得到的最后指标评价中的权重。

三、实案分析

利用以上权重计算方法，研究我国装备制造业创新能力评价指标的权重。现以在A股上市公司中的装备制造业企业创新能力为研究对象，首先分别计算评价指标的主、客观指标权重值，然后对主、客观指标权重进行综合计算，最后获得装备制造业企业创新能力评价指标权值。

(一)客观重要度计算

为获得准确的样本数据，选择在我国A股上市的34家装备制造业企业为研究对象，并以2012年年报数据为基础，从中抽取评价指标的样本值，则可设样本集合U={x1，x2，…，x34}。条件属性参考并综合已有研究成果［25-28］，选择11个指标作为评价指标项，并构建指标集合C={政府科技经费补贴，年度净利润，技术人员占就业比重，R＆D投入金额，R＆D研发支出占营业收入比例，R＆D投入增长率，在研发新产品数量，新产品占销售产品的比重，当年申请专利数，科技研发获奖在同行业中的比例，有无核心产业链上的重组兼并活动}，简记为 C={c1，c2，…，c11}，D={创新能力高，创新能力低}。当样本数量并非远远大于条件属性数量时，为防止出现多数条件属性重要性为0值的情况，将条件属性和决策属性判断分为高、低两个级别。高时取2值，低时取1值，则可建立的一个决策判断矩阵，如表1所示。

1.计算各属性等价类

首先计算决策属性和条件属性集合的等价类。

U/IND(D)={{1，2，4，5，6，7，13，14，15，17，18，21，26，29，31，33，34}，{3，8，9，10，11，12，16，19，20，22，23，24，25，27，28，30，32}}

U/IND(C)={{1}，{2}，{3}，{4}，{5}，{6}，{7}，{8}，{9}，{10}，{11}，{12}，{13}，{14}，{15}，{16}，{17}，{18}，{19}，{20}，{21}，{22}，{23}，{24}，{25}，{26}，{27}，{28}，{29}，{30}，{31}，{32}，{33}，{34}}

然后，分别移去各条件属性，计算等价类U/IND(C-ci)。

U/IND(C-c1)={{1}，{2}，{3}，{4}，...，{31}，{33}}

U/IND(C-c2)={{1}，{2}，{3}，{4}，...，{33}，{34}}

U/IND(C-c3)={{1}，{2}，{3}，{4}，...，{31}，{34}}

U/IND(C-c4)={{1，21}，{2}，{3}，{4}，...，{33}，{34}}

表1 样本决策表示

U/IND(C-c5)={{1}，{2，26}，{3}，{4}...，{33}，{34}}

U/IND(C-c6)={{1}，{2，8}，{3}，{4}，...，{33}，{34}}

U/IND(C-c7)={1}，{2}，{3，31}，{4}，...，{33}，{34}}

U/IND(C-c8)={{1}，{2}，{3}，{4，29}，...，{33}，{34}}

U/IND(C-c9)={{1，13}，{2}，{3}，{4}，...，{32}，{33}}

U/IND(C-c10)={{1}，{2}，{3}，{4}，...，{33}，{34}}

U/IND(C-c11)={{1}，{2}，{3}，{4}，，...，{33}，{34}}

2.计算各属性的正域

POSC(D)={1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34}

POS{C/c1}(D)={1，2，3，4，5，6，7，8，9，10，11，13，15，17，18，19，20，22，23，24，25，26，27，28，29，30，31，33}≠POSC(D)

POS{C/c2}(D)={1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，27，28，29，32，33，34}≠POSC(D)

POS{C/c3}(D)={1，2，3，4，5，6，7，8，9，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，30，31，34}≠POSC(D)

POS{C/c4}(D)={2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，22，23，24，25，26，27，28，29，31，32，33，34}≠POSC(D)

POS{C/c5}(D)={1，3，4，5，6，7，8，14，9，10，11，32，12，13，15，16，17，18，19，20，21，22，23，24，25，29，30，31，33，34}≠POSC(D)

POS{C/c6}(D)={1，3，4，5，6，7，9，10，11，12，13，15，16，17，18，19，20，21，22，25，27，28，29，31，33，34}≠POSC(D)

POS{C/c7}(D)={1，2，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，21，22，23，25，26，27，28，29，30，32，33，34}≠POSC(D)

POS{C/c8}(D)={1，2，3，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，30，31，32，33，34}≠POSC(D)

POS{C/c9}(D)={2，3，4，5，6，7，8，9，10，12，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，29，30，31，32，33}≠POSC(D)

POS{C/c10}(D)={1，2，3，4，5，6，8，9，10，11，12，14，15，16，17，18，19，20，23，24，25，26，27，28，29，30，31，32，33，34}≠POSC(D)

POS{C/c11}(D)={1，2，3，4，7，8，10，11，12，13，15，16，18，19，20，21，22，23，24，25，26，27，28，29，31，32，33，34}≠POSC(D)

3.属性重要度计算

根据式(2)计算企业创新能力评价各属性的重要度，得到各属性的重要度，用K表示。

4.计算评价指标权重

对各指标的重要度值进行归一化处理，得到各评价指标的客观权重，用W表示，则每一个指标的权重如下:

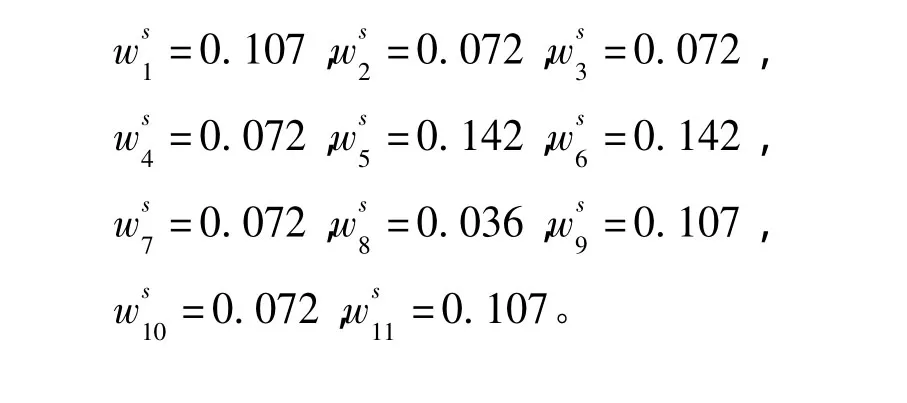
由计算结果可知，在客观权重定义中，R＆D研发支出占营业收入比例、R＆D投入增长率对企业创新能力影响最大，说明企业在创新上的投入是提升企业创新能力的重要因素，其中政府科技经费补贴和有无核心产品链上的重组兼并活动对企业创新影响也较大。

利用粗糙集对样本数据进行的权重计算，容易受样本选择影响，同时未能充分利用领域专家的经验与知识，难免不够准确。本文在客观权重计算的基础上，利用专家问卷打分，获得主观指标权重，在此基础上综合主、客观的权重值，得到一个综合的指标权重。

(二)主观权重计算

设计企业创新能力评价指标体系问卷，为了便于专家打分，设计二级指标，第一级为创新资源、创新投入和创新产出三个指标，二级指标包括上面选择的11个评价指标项，采用9标度法，由专家对两两指标进行重要性对比打分。共发放60份问卷，包括院校专家40份，企业家20份，共收回有效问卷56份。利用AHM方法对问卷数据进行主观指标权重的计算，根据AHM的权重计算过程与步骤。分别对一级指标与二级指标进行打分，计算总的贡献度，即为领域专家主观经验权重值。

1.一级指标权重的确定

一级指标创新资源的权重a1=0.21，创新投入的权重a2=0.41，创新产出的权重a3=0.38。

2.二级指标相对上级目录的权重计算

分别对每一个一级指标中的二级指标进行AHM的计算，可得到11个二级指标分别对上一级目标的评价权重，从c1到c11个指标的值用b表示，则分别为:

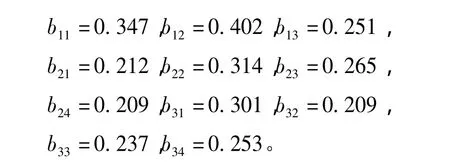
3.二级指标对总目标的贡献权重计算

接着计算11个指标在总评价中的权重值，计算公式为

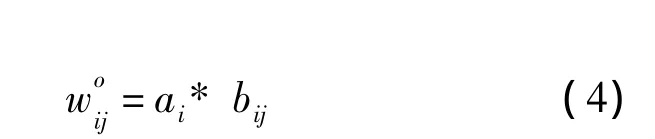
则最终得11个指标在企业创新能力评价中的主观权重如下:

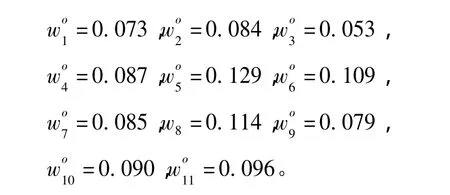
由此则获得了领域专家主观指标权重值，这由28个有效样本获得的指标权重，具有一定的代表性和科学性。

(三)确定组合权重

以上通过粗糙集与AHM分别获得主、客观评价指标的权重，为获得更为科学、合理的指标权重，需要对两组指标进行综合计算，以求得最终的指标权重。在本文的研究中，来自客观数据比较准确，所以对客观指标赋以较大的比重，这里用近似黄金分割点值0.62作为u的赋值，则指标综合算法如公式(5)所示。其中为客观指标权重为主观指标权重。最后得到的企业创新能力评价指标的权重如表2所示。

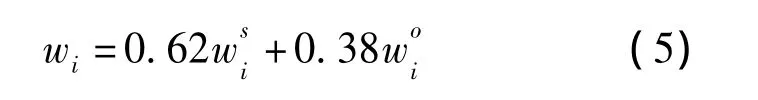
表2 企业创新能力评价指标权重

从综合权重可以看出，R＆D研发支出占营业收入比例指标影响因素最大，这说明资金的投入在企业创新中仍然是重要的因素，企业创新投入的资金越多，对创新的影响越大。R＆D投入增长率影响因素仅次于R＆D研发支出占营业收入比例，说明企业的持续创新能力的重要性。持续创新才能为企业提供源源不断的发展动力。这说明在我国装备制造业企业创新活动中，在创新体制，机制还不完全成熟的环境下，依靠资金投入仍然是企业创新活动的主要手段和方法。

四、结语

评价指标权重是评价是否科学、合理的重要因素。针对装备制造业企业创新能力评价指标体系构建过程单一，受主观因素影响大，且指标集信息冗余的问题，文中提出基于粗糙集理论与AHM相结合的方法，从主、客观两个方面对企业创新能力评价指标的权重进行了计算，并通过文中构建加权权重计算函数计算评价指标的综合权重。文中首先根据已有的研究成果，选择了11项装备制造业企业创新能力评价指标，然后从A股上市公司中选择34家上市公司2012年年报数据为基础，构建样本数据，并利用粗糙集理论计算各评价指标的客观权重。同时为了充分利用专家经验以克服客观赋中容易受样本选择的影响不足，通过专家问卷，并利用AHM方法对问卷数据进行主观权重的计算，最后对主、客观获得的权重进行综合，从而得到一个最终的装备制造业企业创新能力评价指标的权重。这一权重值与传统的基于单一主观或客观的权重确定方法，结果更为科学、合理。本方法的不足是当指标项较多时，需要较大的样本量才能得到客观指标权重值，同时主、客观指标权重在综合计算时的u值需要专家给出，易受人为因素的影响。以上两点不足，在后续研究中需要进一步加以改进。

［1］李京文，黄鲁成.关于我国制造业创新战略的思考［J］.中国软科学，2003(1):23-26.

［2］杨华峰，申 斌.装备制造业原始创新能力评价指标体系研究［J］.工业技术经济，2007(11):85-89.

［3］吴 雷，陈 伟.基于DEA的装备制造业技术创新能力的评价研究［J］.科技管理研究，2009(6):45-46.

［4］CHEN S W，WANG DH.Study on technological innovation ability evaluation of IT industry in China［C］.2006 IEEE International Conference on Management of Innovation and Technology，2006:230-234.

［5］GRUPP H，SCHUBERT T.Review and new evidence on composite innovation indicators for evaluating national performance［J］.Research Policy，2010，39(1):67-78.

［6］毕克新，张淑芳.基于产品创新能力的制造企业产品创新模型选择［J］.中国青年科技，2007(4):23-26.

［7］HUANG L H，LUO YF，ZHANG H，et al.Technology innovation ability analysis of beijing's manufacturing industry［C］.2006 IEEE International Conference on Management of Innovation and Technology，2006:195-201.

［8］吴殿廷，李东方.层次分析法的不足及其改进的途径［J］.北京师范大学学报:自然科学版，2004，40(2):264-268.

［9］单红梅.企业技术创新绩效的综合模糊评价及其应用［J］.科研管理，2002，23(6):120-124.

［10］鲍新中，张建斌，刘 澄.基于粗糙集条件信息熵的权重确定方法［J］.中国管理科学，2009，17(3):131-135.

［11］栾大龙，铉一民，姚彬，等.基于粗糙集——主成分分析的企业创新能力评价实证研究［J］.计算机工程与应用，2007，43(4):207-209.

［12］陶菊春，吴建民.综合加权评分法的综合权重确定新探［J］.系统工程理论与实践，2001，8(44):E4.

［13］毛定祥.一种最小二乘意义下主客观评价一致的组合评价方法［J］.中国管理科学，2002(5):95-97.

［14］张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京:科学出版社，2000.

［15］郭艳红.基于均方差分析法的北京市土地资源承载力评价［J］.资源与产业，2011，13(6):63-65.

［16］BARTHOLOMEW D J，KNOTT M，MOUSTAKI I.Latent Variable Models and Factor Analysis:A Unified Approach［M］.Wiley.com，2011.

［17］GRAY R M.Entropy and information theory［M］.Springer，2011.

［18］曹庆奎，任向阳，刘 琛，等.基于粗集——未确知测度模型的企业技术创新能力评价研究［J］.系统工程理论与实践，2006(4):67-72.

［19］刘希宋，李 玥.基于粗糙集理论的企业自主创新能力评价研究［J］.科技进步与对策，2008，25(1):135-138.

［20］PAWLAK Z.Rough set theory and its applications to data analysis［J］.Cybemetics and Systems，1998，29(1):661-688.

［21］HAN J W，KAMBER M.Data mining:Concept and Tech-niques［M］.Morgan Kaufmann Publishers ins，2001.

［22］李小霞，陈绵云.粗糙集理论中的决策表条件属性的简化［J］.华中科技大学学报:自然科学版，2003，31(8):85-87.

［23］李廉水，王桂芝，黄小蓉，等.气象灾害评估分析的AHM方法研究［J］.数理统计与管理，2011，30(2):201-205.

［24］李滨江.基于AHM方法的高技术项目全生命周期风险集成评价方法研究［J］.价值工程，2012，31(14):162-163.

［25］郑若谷.中国制造业产业自主创新能力评价［J］.当代财经，2010(1):89-95.

［26］杨振宇.创业板上市公司财务指标的统计分析［J］.科技创业月刊，2010(11):1-8.

［27］张梦露，张忠家.基于因子分析法的湖北省制造业技术创新能力评价研究［J］.科技进步与对策，2011，28(18):123-125.

［28］肖德云，树 华，戴 勇.我国制造业自主创新能力综合评价［J］.管理学报，2010，7(7):1008-1014.