如何加深对数学知识的理解和掌握

林丽芳

一、形象操作，激发探究兴趣

在教学《认识面积》一课时，我先从学生已有的知识经验出发，课件出示长方形、三角形、平行四边形等封闭平面图形，在各图中涂上不同的颜色，形成一个面，比较发现物体的各个面形状不同，大小也不尽相同。然后让学生从身边的生活事物中找物体表面，动手摸一摸，感受物体表面有大有小，不尽相同。这个导入，自认为有理有据，顺当得很。可上完课后反思，觉得是老师牵着学生走，学生学习的兴趣不高，学习面积的目的性、必要性没有体现出来。于是，第二次课时，我重新设计了一个情境：爸爸带小明去海边散步，沙滩上留下两行脚印，让孩子们猜一猜、连一连：“哪行脚印是爸爸的，哪行脚印是小明的？”，并说说你是根据什么来猜的；又设置了一个“打补丁”的情境，让学生帮助老奶奶选择一块合适的布料去打补丁。学生兴致勃勃，跃跃欲试，并能自主说出选择的理由，学习气氛截然不同。有了这一教学心得，在教分数加减法时，我给学生每人发一张纸，在这张纸上折出一个自己喜欢的分数，并涂上自己喜欢的颜色，展示作品，读出分数，并用这些分数提出有关分数加减计算的问题。学生思路宽了，活了。通过自主操作、自主提问、自主解答，人人学有价值的数学，培养了学生自主学习的兴趣。

二、表象操作，培养探究意识

数学教学是活动中的教学，为此，教师要根据不同的教学内容，尽可能地让学生折一折、剪一剪、摆一摆、量一量等。精心诱引教学《圆的认识》时，我让学生们剪下一个圆，师：同学们把你所剪下的圆对折，打开，换下个方向再对折，再打开，如此反复折几次，（学生动手操作）师：对折若干次后，你们发现了什么？生1：折痕相交一点，交点在圆的中心。生2：每条折痕一样长，交点把折痕分成了相等的两部分……师：你们有这么多的发现很好，这些折痕相交于圆中心的一点，我们把圆中心的这一点叫作圆心，圆心用字母O表示。师：你们发现圆心把每条折痕分成了相等的两部分，这是凭眼睛估计的，是否真的相等，请同学们拿出尺子量一量，并记录下你们所量的长度。（学生动手操作）发现两部分完全相等。师：请在你们的圆上任取一点，量一量圆心到这点的长度，多做几次，并记录下所量的长度。（学生动手操作，汇报所得数据）师：观察你们所量得的数据，从你们所量的数据中，有没有规律，如果有，这个规律是什么？生1：有规律，每组数据都相等。师：相等说明了什么？生：圆心到圆上任意一点的距离都相等。师：祝贺你们！你们所得出的结论是正确的，从圆心到圆上任意一点的距离都相等，我们把这条线段叫作圆的半径。半径用字母r表示。师：请同学们想一想，在同一个圆内，半径有多少条？它们都相等吗？生：有无数条，都相等。学生在教师的引导下，通过剪一剪、折一折、量一量、比一比的方法，自己发现规律，自己验证结论，主动获取知识，在自主探究知识的过程中培养了创新精神和实践能力。

三、变位操作，提高探究能力

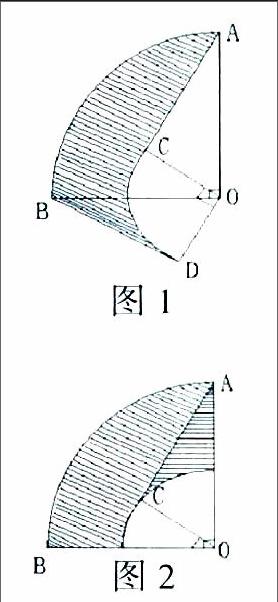
数学学科具有较强的抽象性，而小学生又是以具体形象思维为主。要解决好数学知识的抽象性与学生思维发展的具体性之间的矛盾，常常需要借助动手操作的方法。感觉的通道越多，思维的联系就越快。如图1所示：

要求图中阴影部分的面积。这是一个不规则图形，活像捉一只刺猬，无从下手，怎么办？让学生自主想想办法，有学生就说把这个图形分解成一个三角形和一个四分之一圆，把图中的三角形绕点O顺时针旋转90度，原图变成如图2：

已知线段OA的长度是3厘米，线段OC的长度是1 厘米，点拨后，学生就能通过自主操作活动，发现求阴影部分的面积的方法。学生学得轻松，又学得巧。

四、拓展操作，发展探究思维

手与脑的这种联系，要求教师在指导学生实践操作时，必须把操作与思维活动结合起来。动手操作是促进学生积极思维的重要手段，是新课程倡导的学习方式，小学数学学习过程中，学生在动手操作中能够发现一些数学问题，找到一些数学规律，直观地理解数学知识。

在一个边长是6米的房子的墙角上拴着一只羊，房子的周围是青草，拴羊的绳长4米，请你算一算这只羊能吃到的草的面积是多少平方米？初一看，这道题挺难，凭空想象，房子、墙角、草地、绳子、羊，好乱。不动笔墨不读书，动手画一画、拴羊的墙角看作圆心，拴羊的绳子长4米是半径，羊能吃到的草的面积本应是一个圆的面积，可是羊拴在墙角上，房子不长草，又是正方形，占据整圆的四分之一面积，因此，羊能吃到的草的面积只有圆的面积的四分之三。这样的探索空间较为适宜，学生既有兴趣又知道其中隐藏着秘密，同时明确怎样去探索，通过努力探索出其中的奥秘，很有成就感。长此以往，学生的探究意识增加，自主探究能力自然会提高。

（作者单位：福建泉州市永春县南湖小学）endprint