半群PO（X，Y，θ）的格林关系及正则元

罗永贵，瞿云云

（贵州师范大学数学与计算机科学学院，贵州贵阳550001）

半群PO（X，Y，θ）的格林关系及正则元

罗永贵，瞿云云

（贵州师范大学数学与计算机科学学院，贵州贵阳550001）

摘要：设X和Y是有限非空集合，PO（X，Y）表示从X到Y的所有部分保序映射构成的集合.取定θ∈PO（Y，X），在PO（X，Y）上定义运算◦，如：α◦β＝αθβ，则（PO（X，Y），◦）是一个半群，称为有限部分保序夹心半群，记为PO（X，Y，θ）.半群PO（X，Y，θ）的格林关系及其正则元被刻划了.

关键词：保序；夹心半群；部分映射；格林关系；正则元

设S是一个半群，a，b∈S，如果a和b所生成的主左理想相等，即S1a＝S1b，则称a和b在一个L等价关系中，记为aLb.如果a和b所生成的主右理想相等，即aS1＝bS1，则称a和b在一个R等价关系中，记为aRb.如果a和b所生成的主理想相等，即S1aS1＝S1bS1，则称a和b在一个J等价关系中，记为aJb.令H＝L∩R，D＝L∨R，则H和D也是半群S上的等价关系.这5个关系统称为半群S上的格林关系，它们对半群的代数结构起着非常重要的作用.在半群代数理论中［14］，有限半群上都有D＝L◦R＝R◦L和D＝J.对于格林关系及其正则元的研究目前已有许多结果［1-13］.

设S是一个半群，a∈S.如果存在b∈S使得aba＝a，称a是正则元.如果a2＝a，称a是幂等元.显然，幂等元是正则元.

设X和Y是同型的非空全序集，P（X，Y）表示从X到Y的所有部分映射构成的集合.若α∈P（X，Y）且对任意的x1，x2∈X，x1＜x2有x1α＜x2α，则称α是一个从X到Y的部分保序映射.用PO（X，Y）表示从X到Y的所有部分保序映射构成的集合.取定θ∈PO（Y，X），在PO（X，Y）上定义运算◦如下：α◦β＝αθβ，则（PO（X，Y），◦）是一个半群，称为部分保序夹心半群，记为PO（X，Y，θ）.特别地φ∈PO（X，Y，θ）.在不引起混淆的情况下，可以把α◦β，记为αβ.当X，Y是有限集且｜X｜≥1，｜y｜≥1时，称PO（X，Y，θ）为有限部分保序夹心半群.用εX表示X上的恒等变换，显然PO（X，X，εX）＝POX.设A，B是同型的非空全序集，记

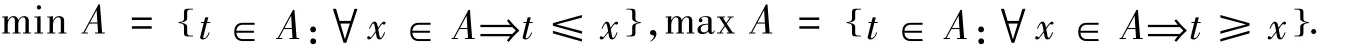
如果∀x∈A⇒x＜min B，∀y∈B⇒y＞max A，则称A＜B.因此，对任意的把α的上述形式称为α的标准表示.

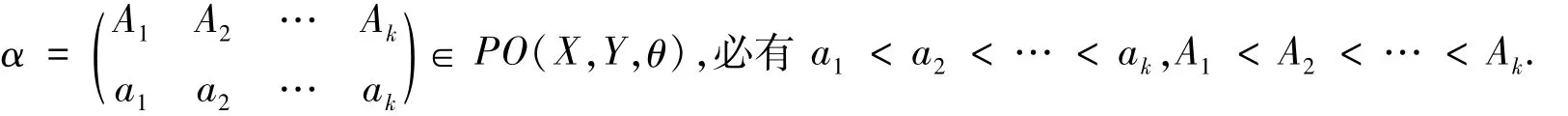
对于半群S上的格林关系“L”，“R”，“H”，“D”，“J”而言.S中的任意一个元素a与它本身总有这5个等价关系，即aLa，aRa，aHa，aDa，aJa是恒成立的.因此，在本文的讨论中要求X和Y是有限集且｜X｜≥2，｜Y｜≥2，｜imθ｜≥2.当讨论半群PO（X，Y，θ）中2个元素α，β是否具有这5个等价关系时，总是假设α≠β.用符号R（PO（X，Y，θ））表示PO（X，Y，θ）的所有正则元构成的集合，用符号E（PO（X，Y，θ））表示PO（X，Y，θ）的所有幂等元构成的集合.特别地φ∈E（PO（X，Y，θ））⊆R（PO（X，Y，θ））.用Lα，Rα，Hα，Dα，Jα分别表示α所在的L-类，R-类，H-类，D-类，J-类.

1 有限部分保序夹心半群PO（X，Y，θ）的格林关系及其正则元

在这里讨论有限部分保序夹心半群PO（X，Y，θ）的格林关系“L”，“R”，“H”，“D”，“J”的充要条件，同时给出了L非平凡和R非平凡的充要条件及其正则元和幂等元的等价条件.

定理1 设α，β∈PO（X，Y，θ），α≠β，则αLβ⇔imα＝imθα＝imθβ＝imβ.

证明 必要性：若αLβ⇒∃ξ，η∈PO（X，Y，θ）∍α＝ξ◦β＝ξθβ，β＝η◦α＝ηθα⇒imα⊆imθβ⊆imβ，imβ⊆imθα⊆imα⇒imα＝imθα＝imθβ＝imβ.

充分性：若imα＝imθα＝imθβ＝imβ，不妨设

令

其中，bi∈ai(θα)-1，ci∈ai(θβ)-1，i＝1，2，…，r.

易见，ξ，η∈PO（X，Y，θ）且ξθα＝ξ◦α＝β，ξθβ＝ξ◦β＝α，即αLβ.

定理2 设α，β∈PO（X，Y，θ），α≠β，则αRβ⇔kerα＝kerαθ＝kerβθ＝kerβ.

证明 必要性：若αRβ⇒∃ξ，η∈PO（X，Y，θ）∍α＝β◦ξ＝βθξ，β＝α◦η＝αθη.由（x，y）∈kerα⇒xα＝yα⇒xαθ＝yαθ⇒xαθξ＝yαθξ（即xβ＝yβ），即kerα⊆kerαθ⊆kerβ.再由（x，y）∈kerβ⇒xβ＝yβ⇒xβθ＝yβθ⇒xαθη＝yαθη（即xα＝yα），即kerβ⊆kerβθ⊆kerα.因此kerα＝kerαθ＝kerβθ＝kerβ.

充分性：若kerα＝kerαθ＝kerβθ＝kerβ，不妨设

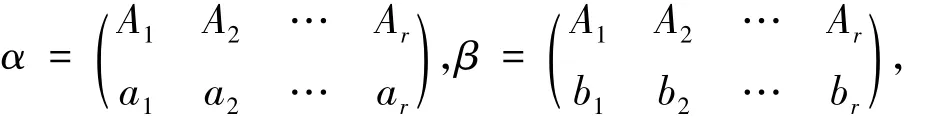
则

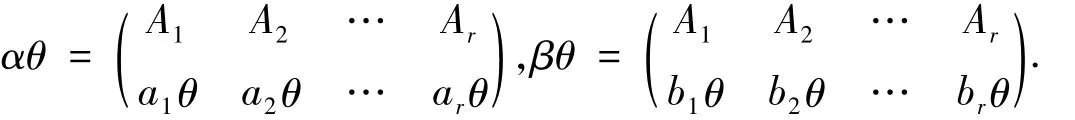
令

易见，ξ，η∈PO（X，Y，θ）且βθξ＝β◦ξ＝α，αθη＝α◦η＝β，即αRβ.

定理3 设α，β∈P（X，Y，θ），则αHβ⇔α＝β.

证明 由定理1，定理2，H＝L∩R及其α，β的标准表示可知该定理成立.

定理4 设α∈PO（X，Y，θ）＼{}φ，则

1）｜Lα｜≥2⇔imα＝imθα；2）｜Rα｜≥2⇔θ｜imα是单射；

证明 1）必要性：若｜Lα｜≥2⇒∃β∈PO（X，Y，θ），α≠β∍αLβ.由定理1可知imα＝imθα＝imθβ＝imβ，即imα＝imθα.

充分性：若imα＝imθα时，

易见，α≠β且imα＝imθα＝imθβ＝imβ.再由定理1可知αLβ，即｜Lα｜≥2.

如果存在某个｜Ai｜≥2(1≤i≤r)，不失一般性，可设｜A1｜≥2，令

如果｜Ai｜＝1(i＝1，2，…，r)，不失一般性，可设x∈X且max A1＜x＜min A2，令

易见，α≠β.再由定理1可知αLβ，即｜Lα｜≥2.

2）必要性：若｜Rα｜≥2⇒∃β∈PO（X，Y，θ），α≠β∍αRβ.由定理2可知kerα＝kerαθ＝kerβθ＝ker β，即kerα＝kerαθ，显然有θ｜imα是单射.

充分性：若θ｜imα是单射时，

易见，α≠β且kerα＝kerαθ＝kerβθ＝kerβ.再由定理2可知αRβ，即｜Rα｜≥2.

定理5 设α∈PO（X，Y，θ）＼{}φ，则α∈R（P（X，Y，θ））⇔imα＝imθα，θ｜imα是单射⇔｜Lα｜≥2且｜Rα｜≥2.

证明 若α∈R（PO（X，Y，θ））⇒∃β∈PO（X，Y，θ）∍α＝α◦β◦α＝αθβθα⇒imα⊆imθα，注意到imθαimα.于是imα＝imθα.∀aα，bα∈imα，若 ( aα)θ＝ (bα)θ，则aα＝aαθβθα＝ ( aαθ)βθα＝(bα θ)βθα＝bαθβθα＝bα，即θ｜imα是单射.

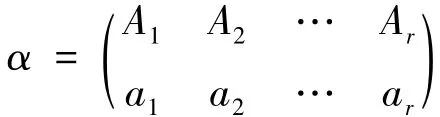
令

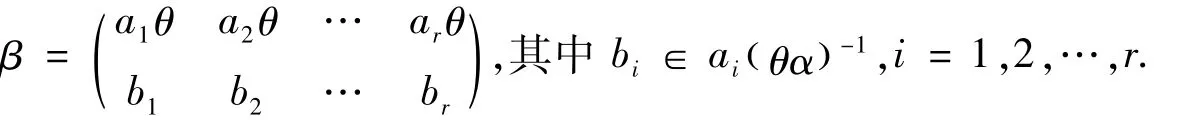
易见，β∈PO（X，Y，θ）且αθβθα＝α◦β◦α＝α，即α∈R（PO（X，Y，θ））.再由定理4可知imα＝imθα，θ｜imα是单射⇔｜Lα｜≥2且｜Rα｜≥2.

定理6 设α∈PO（X，Y，θ）＼{}φ，则

α∈E（PO（X，Y，θ））⇔θα｜imα＝εimα⇔∀z∈imα⇒zθ∈zα-1.

证明 若α∈E（PO（X，Y，θ））⇒α◦α＝αθα＝α，∀b＝aα∈imα⇒bθα＝aαθα＝aα＝b⇒θα｜imα＝εimα.

反之，若θα｜imα＝εimα⇒α＝αθα＝α◦α，从而α∈E（PO（X，Y，θ））.进一步可以验证α∈E（PO（X，Y，θ））⇔∀z∈imα⇒zθ∈zα-1.

定理7 设α，β∈PO（X，Y，θ），α≠β，则αDβ当且仅当下列条件之一成立：

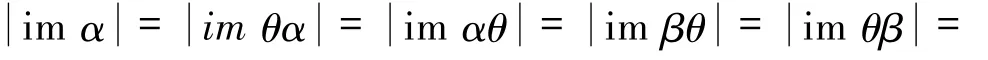
当ξ＝α，ξ≠β时，有αRβ.由定理2可知kerα＝kerαθ＝kerβθ＝kerβ.若imα＝imθα时，结论1）成立.若imα⊃imθα时，结论2）成立.

当ξ≠α，ξ＝β时，有αLβ.由定理1可知imα＝imθα＝imθβ＝imβ.

若kerα＝kerαθ时，结论1）成立.

充分性：2），3）的结论是平凡的.若α，β∈PO（X，Y，θ）且满足（1）的条件，不妨设

imα＝imθα＝imθβ＝imβ，kerα＝kerαθ＝kerβθ＝kerβ且ξ≠α，ξ≠β，

再由定理1，2可知αLξRβ，即αDβ.

引理1［7］在周期半群上D＝J.特别地，有限半群是周期半群，在任意有限半群上都有D＝J.

命题1 有限部分保序夹心半群PO（X，Y，θ）上有D＝J.

证明 由X，Y的有限性可知PO（X，Y，θ）是有限的，再由引理1可知在半群PO（X，Y，θ）上有D＝J.

2 半群RPO（X，Y，θ）的格林关系

这里主要讨论有限部分保序夹心半群PO（X，Y，θ）的所有正则元R（PO（X，Y，θ））构成了PO（X，Y，θ）的子半群.进而对其格林关系进行了研究.

定理8 R（PO（X，Y，θ））作成PO（X，Y，θ）的正则子半群.记为RPO（X，Y，θ）.

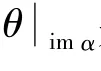
定理9 设α，β∈RPO（X，Y，θ），α≠β，则αLβ⇔imα＝imβ.

证明 必要性：由定理1.1的必要性的证明及其定理5可知必要性的证明是平凡.

充分性：若α，β∈RPO（X，Y，θ），α≠β且imα＝imβ.由定理5可知imα＝imθα＝imθβ＝imβ.进一步可以证明定理1的充分性证明中构造的ξ，η满足：ξ，η∈RPO（X，Y，θ），αLβ.

定理10 设α，β∈RPO（X，Y，θ），α≠β，则αRβ⇔kerα＝kerβ.

证明 必要性：由定理2的必要性的证明及其定理5可知必要性的证明是平凡.

充分性：若α，β∈RPO（X，Y，θ），α≠β且kerα＝kerβ.由定理5可知

kerα＝kerαθ＝kerβθ＝kerβ.进一步可以证明定理2的充分性证明中构造的ξ，η满足：ξ，η∈RPO（X，Y，θ），即αRβ.

定理11 设α，β∈RPO（X，Y，θ），则αHβ⇔α＝β.

证明 由定理9，10及其H＝L∩R和α的记法可知该定理成立.

证明 必要性：由定理1.7的必要性的证明及其定理5可知必要性的证明是平凡.

命题2 在半群RPO（X，Y，θ）上有D＝J.

证明 由X，Y的有限性可知PO（X，Y，θ）是有限的，再由定理8可知RPO（X，Y，θ）是PO（X，Y，θ）的子半群，于是RPO（X，Y，θ）是有限的，注意到引理1可知，在半群RPO（X，Y，θ）上有D＝J.

参考文献：

［1］梁国喜，罗永贵，游泰杰.有限部分夹心半群P（X，Y，θ）的格林关系及其正则元［J］.贵州师范大学学报：教育科学版，2011，52（6）：3-5.

［2］裴惠生，崔红村，金勇.夹心半群T（X，Y；θ）上的最小真同余［J］.数学进展，2004，33（3）：284-290.

［3］裴惠生，崔红村，金勇.夹心半群P（X，Y，θ）上α-同余［J］.数学学报，2004，47（2）：371-384.

［4］裴惠生，孙垒，崔红村，等.TE（X）的变种半群TE（X，θ）的若干性［J］.信阳师范学院学报，2004，17（2）：129-133.

［5］GREEN JA.On the structure of semigroups［J］.Ann.Math，1951，54：136-172.

［6］MAGILL JR K D，SUBBIAH S.Green′s relations for regular elments of sandwich semigroups，（I）general results［J］.Proc London Math Soc，1975，30（3）：194-210.

［7］MAGILL JR K D，SUBBIAH S.Green′s relations for regular elments of sandwich semigroups，（Ⅱ）semigroups of continuous function［J］.Austral Math Soc，1978，25（A）：45-65.

［8］MAGILL JR K D，MISRA PR.Homomorp hisims of sandwich semigroups and sandwich near rings［J］.Semigroup Forum，1993，47：168-181.

［9］MAGILL JR K D，MISRA PR，TEWARIU B.Symons′congruence on sandwich semigroups［J］.Czech Math J，1983，108（33）：221-236.

［10］PEI Hui-sheng.α-congruences on variants of S（X），（I）general results［J］.Joumal of Xinyang Teachers College，1996，9（2）：109-115.

［11］PEI Hui-sheng.α-congruences on variants of S（X），（Ⅱ）α-congruences［J］.Joumal of Xingyang Teachers College，1996，9（3）：217-225.

［12］PEI Hui-sheng，SUN Lei.Green′s relations for the variants of transformtion semigroups preserving an equivalence relation［J］.Communications in.Algebra，2007，35（6）：1971-1986.

［13］SCHEIN B M.Research problems［J］.Semingroup Forum，1970，1：91-92.

［14］HOWIE JM.Fundamentals of semigroup theory［M］.Oxford：Oxford univerify press，1995.

［15］王守峰.半群成群的几个充要条件［J］.云南师范大学学报：自然科学版，2012，32（6）：39-41.

（责任编辑 梁志茂）

中图分类号：O152.7

文献标志码：A

文章编号：1672-8513（2014）06-0434-05

收稿日期：2014-04-16.

基金项目：贵州省科学技术基金（黔LKS（2011）15；LKS（2012）2273）.

作者简介：罗永贵（1985-），男，硕士，讲师.主要研究方向：半群代数理论.

Green′s relations and regularity for the semigroup PO（X，Y，θ）

LUO Yong-gui，QU Yun-yun
（Department of Mathematics and Computer Science，Guizhou Normal University，Guiyang 550001，China）

Abstract：Let X and Y be nonempty finite set.Let PO（X，Y）be all partial order-preserving mapping from X into Y and letθ∈PO（Y，X）.The operation◦is defined byα◦β＝αθβ，for allα，β∈PO（X，Y）.Then（PO（X，Y），◦）is a semigroup and call order-preserving sandwich semigroups of all finite partial mapping from X into Y and so denote PO（X，Y，θ）.The Green′s relations and regularity for the semigroup PO（X，Y，θ）are characterized.

Keywords：order-preserving；sandwich semigroups；partial mapping；Green′s relations；regular element