稀疏随机矩阵有限等距性质分析

张 波 刘郁林 王 开



稀疏随机矩阵有限等距性质分析

张 波*刘郁林 王 开

(重庆通信学院DSP研究室 重庆 400035)

稀疏随机矩阵由于具有存储容量小、编码和重构复杂度低、易于更新等优良特性而适用于分布式应用。为确保稀疏随机矩阵可作为压缩感知观测矩阵，该文证明了稀疏随机矩阵的有限等距性质(RIP)。首先，证明了测量矩阵满足有限等距性质等价于其子矩阵的格拉姆矩阵特征值分布于1附近；在此基础上，证明了当测量值个数满足特定条件时，稀疏随机矩阵以接近于1的概率满足有限等距性质。仿真实验表明，稀疏随机矩阵在保证稀疏信号精确重建的同时，大大节约了测量和重建所需的时间。

压缩感知；稀疏随机矩阵；有限等距性质；测量矩阵

1 引 言

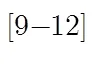
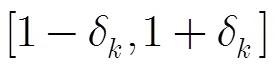
2 基本理论

2.1 压缩感知

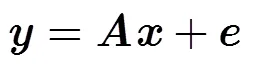
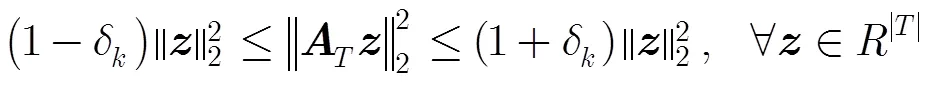
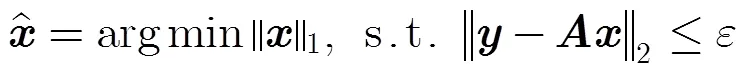
2.2 稀疏随机矩阵

3 有限等距性质的特征值分布条件

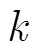
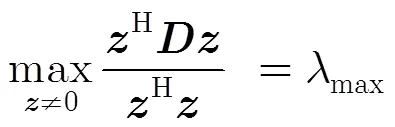
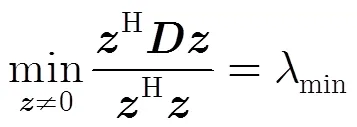
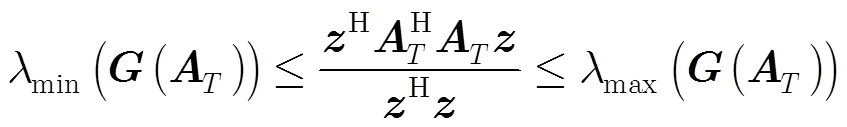
即

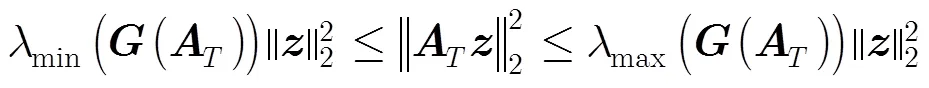
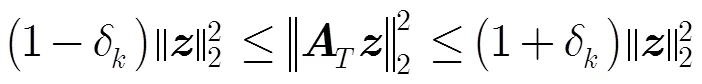
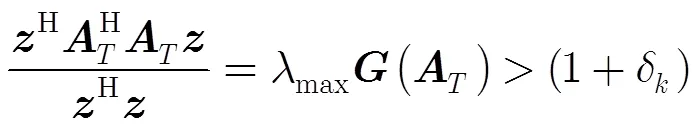
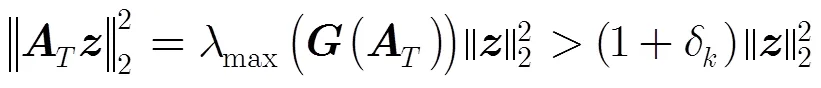
4 稀疏随机矩阵有限等距性质分析

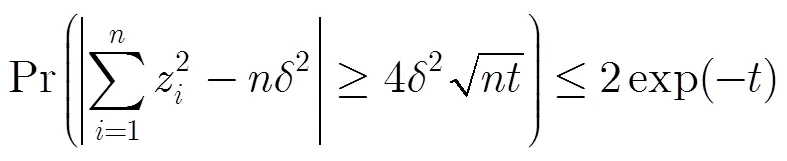
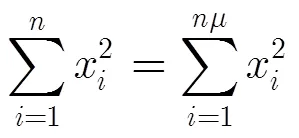
证毕

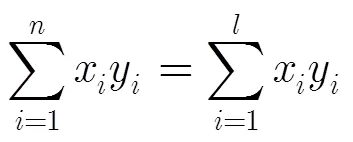
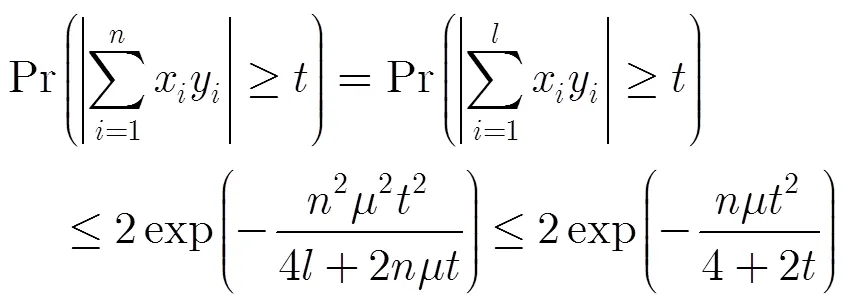
证毕

借助以上引理可证明稀疏随机矩阵满足有限等距性质。

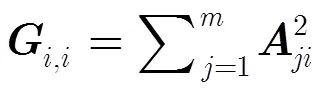
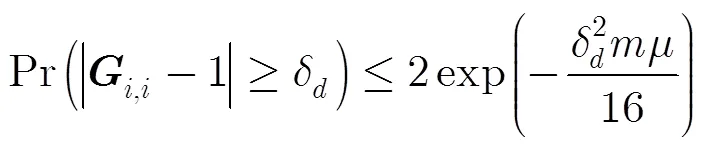
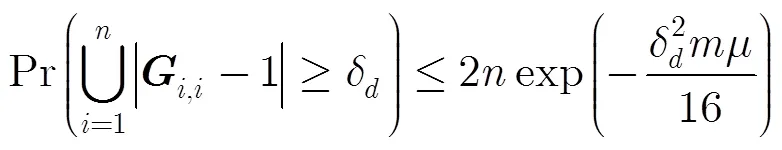
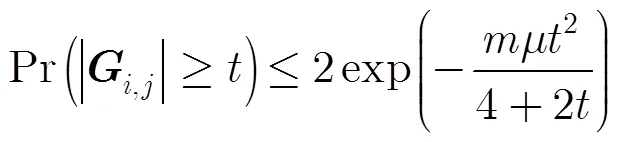
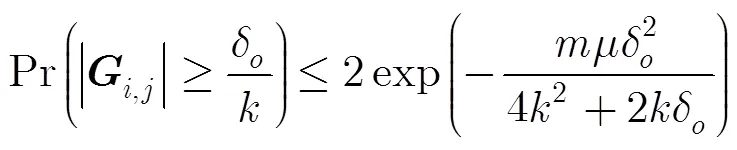
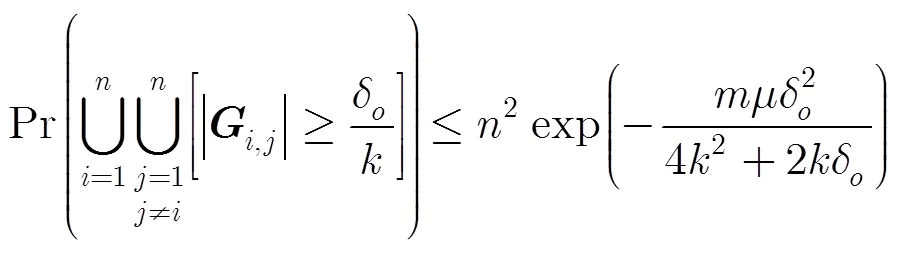
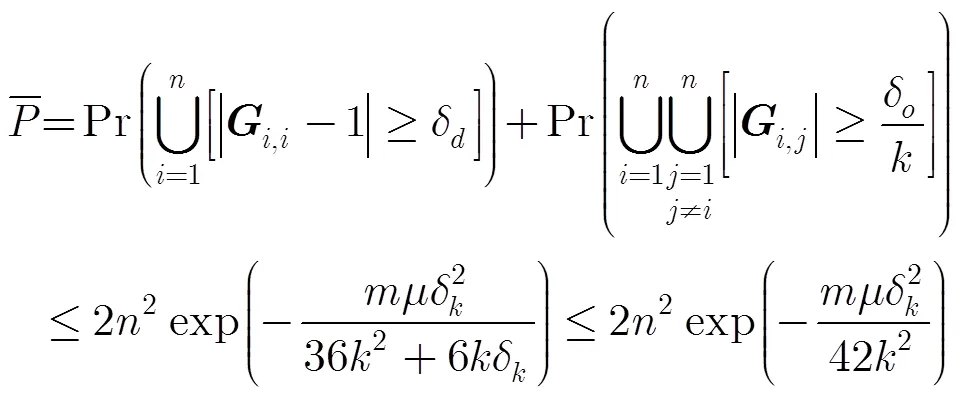
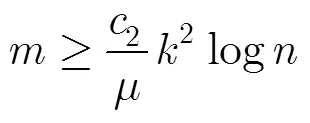
则有

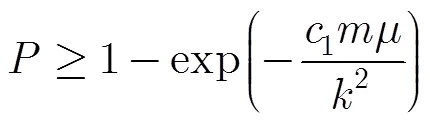
证毕

5 仿真实验

本节将通过仿真实验分析稀疏随机矩阵的性能，验证稀疏随机矩阵作为压缩感知观测矩阵的可行性和实用性。

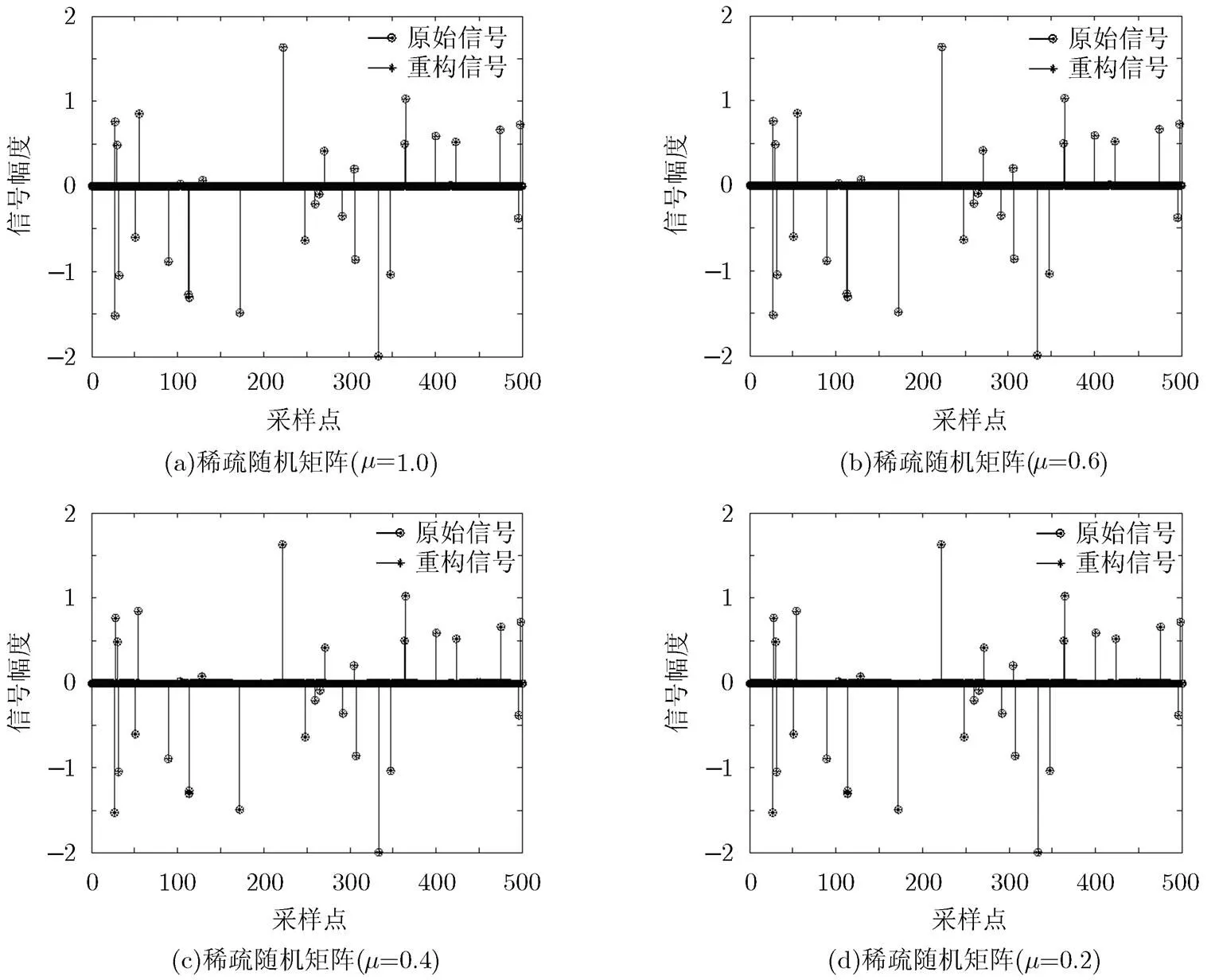
图1 1维稀疏信号重建

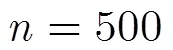
结合以上仿真结果可知：对稀疏随机矩阵加入大量零元素，可在略微增加精确重建所需的测量值个数的情况下，大大减少测量和重建时间，对于图像压缩传感、传感器网络数据压缩传感等实际应用具有重要的意义。

图2 重建成功率比较

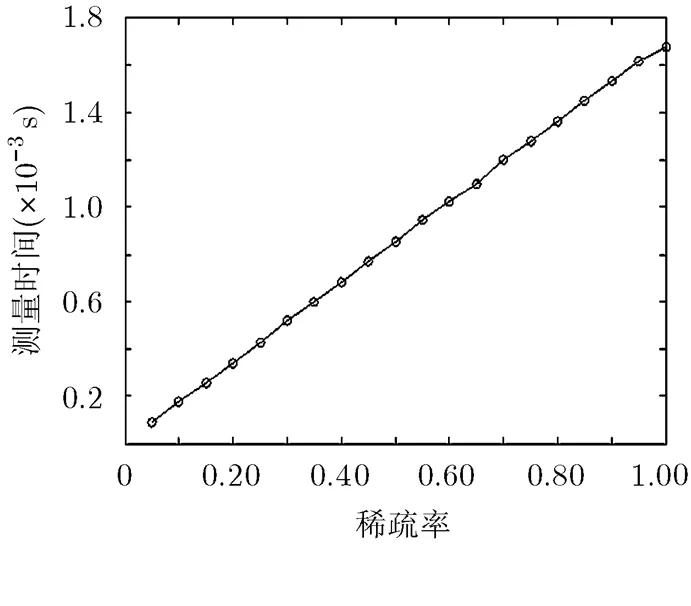
图3 测量时间随测量矩阵稀疏率变化情况

6 结束语

测量矩阵满足RIP是确保重构稀疏信号的充分条件。本文证明了稀疏随机矩阵满足RIP，为应用稀疏随机矩阵作为CS观测矩阵解决实际问题提供了理论指导。该证明分两步进行：首先，推导得到了测量矩阵满足RIP的特征值分布条件，将RIP的证明问题转化为格拉姆矩阵特征值分布范围的讨论问题；然后，证明了当测量值个数满足特定条件时，稀疏随机矩阵以接近1的概率满足RIP。下一步将以本文的结论为基础，针对WSNs的具体应用，深入研究适用于WSNs数据收集的稀疏测量矩阵设计问题。

[1] Donoho D L. Compressed sensing[J]., 2006, 52(4): 1289-1306.

[2] Candes E J and Tao T. Decoding by linear programming[J]., 2005, 51(12): 4203-4215.

[3] Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.

[4] CandesE J, EldarYC, NeedellD,.. Compressed sensing with coherent and redundant dictionaries[J]., 2011, 31(1): 59-73.

[5] Zhang T. Sparse recovery with orthogonal matching pursuit under RIP[J]., 2011, 57(9): 6215-6221.

[6] Haupt J, Bajwa W, Raz G,.. Toepitz compressed sensing matrices with applications to sparse channel estimation[J]., 2010, 56(11): 5862-5875.

[7] Luo J, Liu X, and Rosenberg C. Does compressed sensing improve the throughput of wireless sensor networks?[C]. IEEE International Conference on Communications, Cape Town, 2010: 1-6.

[8] Lee S, Pattem S, Sathiamoorthy M,.. Spatially-localized compressed sensing and routing inmulti-hop sensor networks[C]. Proceedings of the Third International Conference on Geosensor Networks, Oxford, 2009: 11-20.

[9] Wang Wei, GarofalakisM, and RamchandranK. Distributed sparse randomprojections for refinable approximation[C].IEEE International Symposium on Information Processing in Sensor Networks,Cambridge,2007: 331-339.

[10] Gilbert A and Indyk P. Sparse recovery using sparse matrices [J]., 2010, 98(6): 937-947.

[11] Wu K and Guo X. Compressive sensing with sparse measurement matrices[C]. Proceedings of the 73rd IEEE Vehicular Technology Conference, Budapest, 2011: 1-5.

[12] 孙晶明, 王殊, 董燕. 稀疏随机矩阵的观测次数下界[J]. 信号处理, 2012, 28(8): 1156-1163.

Sun Jing-ming, Wang Shu, and Dong Yan. Lower bounds on the number of measurements of sparse random matrices[J]., 2012, 28(8): 1156-1163.

[13] CandesEJ, RombergJ, and TaoT. Stable signal recovery from incomplete and inaccuratemeasurements [J]., 2006, 59(8): 1207-1223.

[14] CaiT T, WangL, and Xu G W. New bounds for restricted isometry constants[J]., 2010, 56(9): 4388-4394.

[15] Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]., 2007, 53(12): 4655-4666.

[16] 甘伟, 许录平, 苏哲, 等. 基于贝叶斯假设检验的压缩感知重构[J]. 电子与信息学报, 2011, 33(11): 2640-2646.

Gan Wei, Xu Lu-ping, Su Zhe,.. Bayesian hypothesis testing based recovery for compressed sensing[J].&, 2011, 33(11): 2640-2646.

[17] Liu Y L, Wang K, and He J W. Signal recovery by compressed sensing in IR-UWB systems[J]., 2012, 21(2): 339-344.

张 波： 男，1987年生，硕士，助教，研究方向为压缩感知、无线传感器网络.

刘郁林： 男，1971年生，教授，博士生导师，研究方向为盲信号处理、超宽带通信、无线传感器网络等.

王 开： 男，1984年生，硕士，讲师，研究方向为超宽带通信、压缩感知及其应用.

Restricted Isometry Property Analysis for Sparse Random Matrices

Zhang Bo Liu Yu-lin Wang Kai

(,,400035,)

Sparse random matrices have attractive properties, such as low storage requirement, low computational complexity in both encoding and recovery, easy incremental updates, and they show great advantages in distributed applications. To make sure sparse random matrices can be used as the measurement matrix, the Restricted Isometry Property (RIP) of such matrices is proved in this paper. Firstly, it is shown that the measurement matrix satisfies RIP is equivalent to the Gram matrix of its submatrix has all of eigenvalues around 1; then it is proved that sparse random matrices satisfy RIP with high probability provided the numbers of measurements satisfy certain conditions. Simulation results show that sparse random matrices can guarantee accurate reconstruction of original signal, while greatly reduce the time of measuring and reconstruction.

Compressed Sensing (CS); Sparse random matrix; Restricted Isometry Property (RIP); Measurement matrix

TN911.72

A

1009-5896(2014)01-0169-06

10.3724/SP.J.1146.2013.00023

2013-01-8收到，2013-10-21改回

教育部新世纪优秀人才支持计划(NCET-10-0873)，重庆市自然科学基金重点项目(CSTC2011BA2016)，重庆高校创新团队建设计划(KJTD201343)和重庆市基础与前沿研究计划项目(cstc2013jcyjA 40045)资助课题

张波 zhangboswjtu@163.com