基于Memetic算法的DNA序列数据压缩方法

谭 丽 孙季丰 郭礼华



基于Memetic算法的DNA序列数据压缩方法

谭 丽*孙季丰 郭礼华

(华南理工大学电子与信息学院 广州 510641)

该文提出一种基于CPMA(Collaborative Particle swarm optimization-based Memetic Algorithm) 算法的DNA序列数据压缩方法，CPMA分别采用综合学习粒子群优化(Comprehensive Learning Particle Swarm Optimization, CLPSO)算法和动态调整的混沌搜索算子(Dynamic Adjustive Chaotic Search Operator, DACSO)进行全局搜索和局部搜索。该文采用CPMA寻找全局最优的基于扩展操作的近似重复矢量(Extended Approximate Repeat Vector, EARV)码书，并用此码书压缩DNA序列数据。实验结果表明，CPMA比其它优化算法有很大的改善，对文中采用的大部分测试函数，其解都非常接近全局最优点；对于DNA基准测序序列，与文中所列的经典DNA序列压缩算法相比，基于CPMA算法的压缩性能得到了显著提升。

DNA序列压缩；Memetic算法；扩展的近似重复矢量(EARV)；粒子群优化(PSO)；动态混沌局部搜索

1 引言

DNA(DeoxyriboNucleic Acid)是由多个核苷酸头尾相连而成的生物大分子化合物，是储存、复制和传递遗传信息的主要物质基础[1]。随着人类DNA序列测定工程的快速发展，DNA序列数据压缩技术的研究已经成为人们关注的热点之一。如何在有限的存储资源内有效储存急剧膨胀的DNA序列数据，用较小的存储空间存放较大的DNA序列数据是计算机专家和生物学家面临的新课题。

由于DNA序列数据的特殊性，使用传统的压缩算法并不是很理想。由此出现了许多专门针对DNA序列的压缩算法，如GenCompress[2], DNApack[3], GeNML[4]等。这些算法大部分都属于基于替代的压缩算法，主要是利用了DNA序列数据中的冗余特性 (如直接重复、镜像、反转和互补回文)，使用了基于字典或其它更为简略的表达方式去替代存储匹配的DNA序列子串，以达到压缩的目的。然而DNA序列数据压缩算法的性能评价标准[5]表明，已有的DNA压缩算法存在耗时长，资源消耗大，压缩性能不稳定等问题。针对以上问题，纪震等人[6]于2010年首次将DNA序列数据的生物信息学特征和生物学含义引入到压缩处理中，打破了以往仅从数据构成特点入手的DNA序列压缩算法模式。文献[7]提出一种在线DNA压缩机算法(DNA Sequence Compressor, DNASC)，该算法从水平和垂直方向对DNA序列数据进行在线压缩，最大特点是基于替代和统计的混合算法。2012年，文献[8]又提出基于自配置单粒子优化的DNA序列压缩算法(Self-Configuration Single Particle Optimizer, SCSPO)，采用自配置结构的粒子群优化算法优化码书，然后利用此码书压缩DNA序列数据，从而达到较好的压缩效果；该算法成功地将智能优化算法应用于DNA序列数据的压缩过程。

本文借鉴SCSPO算法思想，提出了另外一种基于Memetic算法的DNA序列数据的压缩方法(Collaborative Particle swarm optimization-based Memetic Algorithm, CPMA)。CPMA算法将综合学习粒子群优化算法 (Comprehensive Learning Particle Swarm Optimizer, CLPSO)[9]作为全局搜索，同时设计出一种动态调整的混沌搜索算子(Dynamic Adjustive Chaotic Search Operator, DACSO)作为局部搜索，两者引入到Memetic算法框架协同进化，找出全局最优的基于扩展操作的近似重复矢量(Extended Approximate Repeat Vector, EARV)码书，用于DNA序列数据的压缩处理。

2 基于扩展操作的近似重复矢量(EARV)码书模型

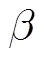
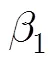
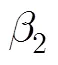
(3)字符串删除(Delete string)：记为(Ds, pos,len)，表示删除序列子串中从pos开始的长度为len的字符串。，采用ARV编码所需的编辑操作比特数目=len，则-= (len -2)´+5´len-3，因len>1，所以(-)>0，即<；

(4)字符交换(Exchange)：记为(, pos1, pos2)，表示交换序列子串中pos1位置和pos2位置的字符。=3+2´，采用ARV编码所需的编辑操作比特数目=2，则计算可得-=7>0，即<；

(5)反序(Inversion)：记为(Inv, pos, len)，其中pos为待反序串的起始位置，len为待反序串的长度。=3+2´，采用ARV编码所需的编辑操作比特数目=len，因len>1，有<。

从以上定义及分析可知，EARV比ARV编码所需的比特数更少。

假设有如下一段DNA序列：

图1中的EARV编码后的4个参数分别代表相对位置，重复模式种类，编辑距离和编辑操作。假设第1个碱基片段“AATCTG”在序列(*)中的绝对位置为1，在模式下对模式串“AACTG”的第3个位置前插入碱基“T”就可以得到碱基片段“AATCTG”，该近似重复矢量可表示为{1,,1,(Insc, 3,T)}；同样在序列(*)2绝对位置处的第2个碱基片段“GCCAA”，近似重复矢量标记为{2-1,,1,(, 2,C)}，表示模式串“AACTG”在镜像匹配下将第2个碱基替换为碱基“C”，2-1表示第2个碱基片段“GCCAA”相对于第1个碱基片段“AATCTG”的位置。序列(*)中其余3个近似片段的EARV编码过程类似。

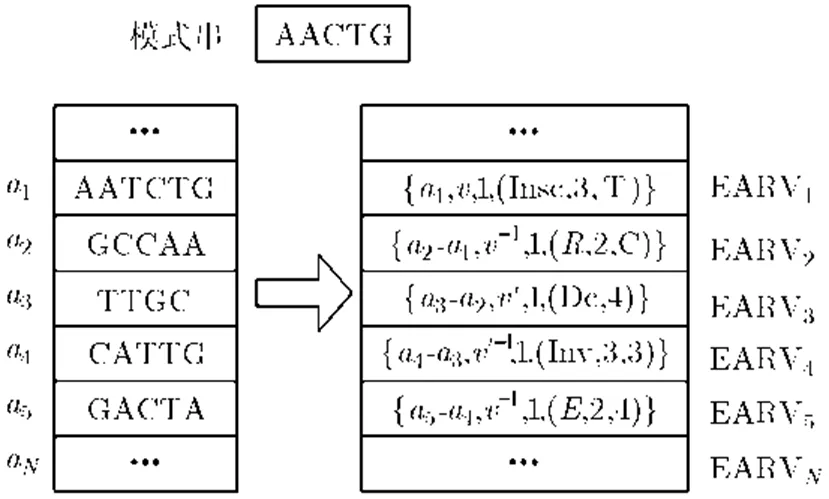
图1 EARV码书中的近似匹配实例

3 基于Memetic算法的DNA序列数据压缩方法

与单纯的进化算法相比，Memetic算法往往能以更少的计算代价，得到具有更高精确度的解，在解决复杂、高维、大规模问题时具有明显的优势[11]，近年来受到了国内外学者的重视。考虑到Memetic算法是基于种群全局搜索和个体局部搜索的混合方法，本文提出了一种基于CPMA的DNA序列数据压缩方法。

3.1 粒子编码和适应度函数的计算

将每个EARV按顺序连接，构造CPMA寻优粒子的位置矢量，对其进行粒子编码，如图2所示，其中,分别表示码书中EARV的长度和数量。

图2 使用EARV码书模型构造寻优第i个粒子

适应度函数的计算过程如图3所示，先将寻优粒子位置矢量离散切分为含有EARV的码书，接着用AGREP[12](Approximate Global search Regular Expression and Print out the line)近似搜索DNA原始序列中含有的EARV，最后将DNA序列数据的压缩率(Bit Per Base, BPB)作为CPMA的适应度函数值：

其中base表示待压缩的DNA序列中碱基个数，bit为编码这些碱基所需的比特数目。适应度函数值越小，说明对DNA序列数据的压缩率越低，即压缩性能就越好。

式(1)的bit计算如式(2)：

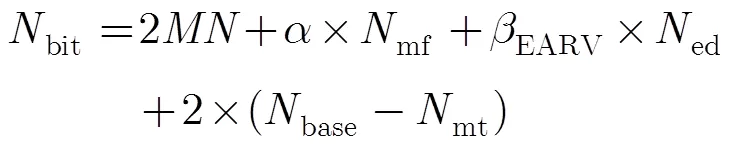
对式(2)进一步说明如下：

(1)存储编码所用的码书，需要(2) bit；

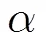
(3)ed表示编辑操作的个数。为描述一个编辑操作所需的平均比特数目，各编辑操作所使用的比特数目在第2节已做分析；

(4)mt表示与码书中的某模式串形成“匹配”的基本碱基个数。base-mt表示未形成“匹配”的碱基总个数，每个碱基的编码采用2 bit的基本编码。

初始化一粒子群，包含ps个粒子，一个粒子代表一个码书，维度为。则寻优粒子位置矢量离散切分为含有EARV的码书过程如下：

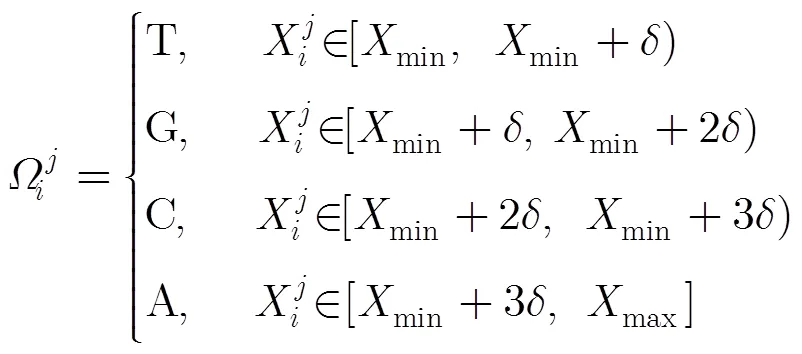
3.2 全局搜索

在CPMA算法中，采用CLPSO作为全局搜索策略，以保证粒子种群的多样性。CLPSO算法的速度和位置更新公式[9]如式(4)至式(7)：

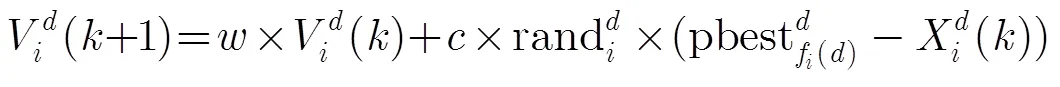
(5)

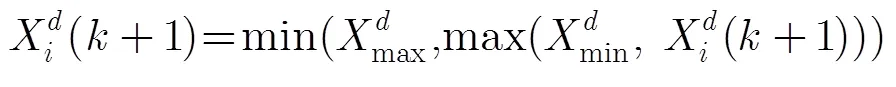
其中为粒子速度矢量，为位置矢量。变量为当前更新粒子的序号，为粒子的维数(0<<),为迭代次数；为惯性权重；rand为[0,1]范围内的均匀随机数；为学习因子；f()表示粒子在第维的学习对象。式(5)和式(7)分别控制粒子的速度和位置范围为[min,max], [min,max]。

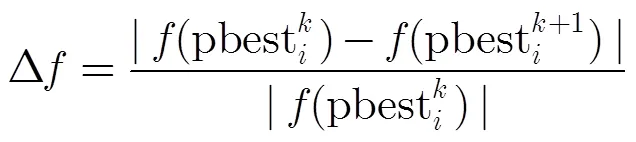
其中pbest和pbest+1分别表示第个粒子在和+1次更新后的局部最优位置。

依次考察粒子的第维速度值V，与停滞速度阈值V作比较，若V<V，则用混沌搜索算子(Chaotic Search Operator, CSO)对粒子进行局部搜索。为了从当前种群中挑选出合适的粒子进行局部搜索，本文采用DACSO的方法，在上一次的局部搜索过程中，若搜索出较多的更优粒子，则在下一次的搜索中，增加其搜索比重。本文中的局部搜索主要针对活泼粒子，采取的策略是：设定活跃系数ca和引入差值系数cd。这两个系数分别动态调整和混沌搜索次数，以使优秀粒子被赋予更多的搜索机会，使非优秀粒子减少搜索机会，以使局部搜索占用的计算开销更有意义。其中第个粒子的活跃系数ca定义为式(9)。

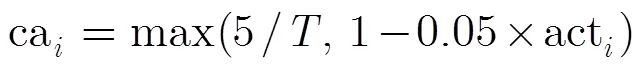
其中act表示上一次的局部搜索中粒子寻优成功的次数。

CPMA算法的具体步骤如表1所示。

3.3 局部搜索

考虑到将局部搜索策略应用到每一个粒子上进行搜索，会大大增加算法的运行时间成本，本文采用了DACSO的局部搜索方法。在DACSO中通过cd去动态调整混沌搜索次数，使其在较少的计算次数内获得更大的性能提升。差值系数cd定义为式(10)

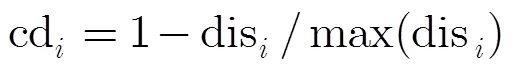
其中dis=|(pbest)-(gbest)。同时本文还引进动态收缩半径的机制，并在收缩区域内随机产生粒子来替代性能较差的粒子，如式(11)：

表1 CPMA算法的具体步骤

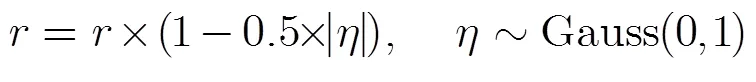
其中随着进化迭代次数的增加而动态地变小，其值越小说明DACSO的搜索范围越小；服从期望值为0，方差为1的高斯分布。设置混沌初始值cx1= rand(01)，混沌搜索半径的初值1=(max-min)/2，令=1, DACSO的局部搜索方法步骤如表2所示。

表2 DACSO的局部搜索方法步骤

整体上来说，CPMA算法根据式(8)从群体中选出备用粒子再进行局部搜索。随着迭代的进行，局部搜索DACSO的频率呈上升趋势，全局搜索CLPSO根据DACSO的反馈进行粒子间的信息交流，再将结果作用于式(8)，选定新一代即将进行局部搜索的粒子。

4 实验结果

4.1 参数设置

本实验将CPMA与其它4种PSO改进算法(CLPSO[9], CEPSO9[14], ISPO[15], SCSPO[8])分别对19个高维测试函数集[16]和11条DNA基准测序序列[17]进行实验。其中，19个高维测试函数具有不同的特点，如单峰或高峰函数、随着维度的增加是否更加容易被优化等；11条DNA基准测序序列来源于美国基因数据库(GenBank)，包含了不同物种不同功能的DNA数据片段，能够有效评估压缩算法对含有不同特征的DNA序列的压缩能力。我们设置各算法对19个高维测试函数分别在维度=100和=500各执行25次，且每次执行中函数的最大计算次数MaxFEs为5000´, 5种比较算法的参数设置如表3所示。

表3各算法的参数设置

算法参数 CLPSO[9]|ps|=10, w:0.9~0.4, c=1.49445, m=8 CEPSO9[14]|ps|=10, w=0.8, c1=c2=2 ISPO[15]J=30, a=150, p=10 SCSPO[8]|ps|=10, w=0.5, c1=c2=2, M=10, N=30 CPMA|ps|=10,fs=1E-6,Vs=1E-4,T=200,cnt=100

表3中，CPMA算法中的全局搜索CLPSO参数0,1,,的设置同文献[9]；实验中为更好地选择进行局部搜索的粒子，一般取f<1E-3；经考察测试函数在迭代中各粒子的变化趋势，发现连续不变或极小变化的次数一般小于1E+3所以<1E+3; CPMA算法中粒子各维速度的更新主要是在全局搜索CLPSO中进行，到进化中后期其值将变得非常小，V>1E-7则可改善CPMA在进化中前期LS搜索率过低的问题；cnt的取值在1E+2左右能较好地平衡全局和局部搜索。除此之外，粒子的位置搜索范围[min,max]设置见文献[16]。

4.2 19个高维测试函数

5种PSO改进算法在=100和=500下对19个高维测试函数的平均误差值对比结果分别见表4和表5。做“显著性水平”的判断是为了说明算法之间的差异是否属于机会变异，即是否具有统计上的显著差异，由此来帮助分析算法的性能。本文显著性水平测试是在各个函数上，将不同算法运行25次产生的适应值数据序列，进行双尾配对样本t检验(two-tailed paired t-test)，其中显著性水平因子= 0.05。表4和表5中符号“†”表示统计显著优胜值，其实验结果值小于近似零处理。

由表4和表5数据可知，与其它4种优化算法相比，CPMA算法在测试函数1,6,7,9～12,15,16,18和19上的平均误差值均取得最佳结果；相对CLPSO算法，CPMA算法在大部分测试函数上都能达到较好的结果(除3,5以外)，尤其在部分函数(1,6,7,10,15和19)的优化上达到或非常接近理论最优值，显示出局部搜索DACSO较好的性能，同时，在函数2,3,8,13和17上，两个算法的优化性能相当；CEPSO9算法是5种改进算法中优化效果最差的算法，其所有的平均误差值都远大于其它算法的优化结果，故CEPSO9算法应用于优化高维多模函数时有待进一步改进；SCSPO算法的平均误差值优化结果全部优于ISPO算法的优化结果，这主要是因为SCSPO算法是在ISPO算法基础上添加了自适应处理机制，从而使得高维多模函数的优化性能得以提升。但与CPMA算法比较，在19个高维测试函数中除了2,3,8,13,14和17以外，其优化性能都不及CPMA算法。配对t检验结果表明，相对其它算法CPMA在函数1,6,7,10,15和19上是统计显著的，具有统计学意义。

表4各算法在=100的平均误差值优化结果

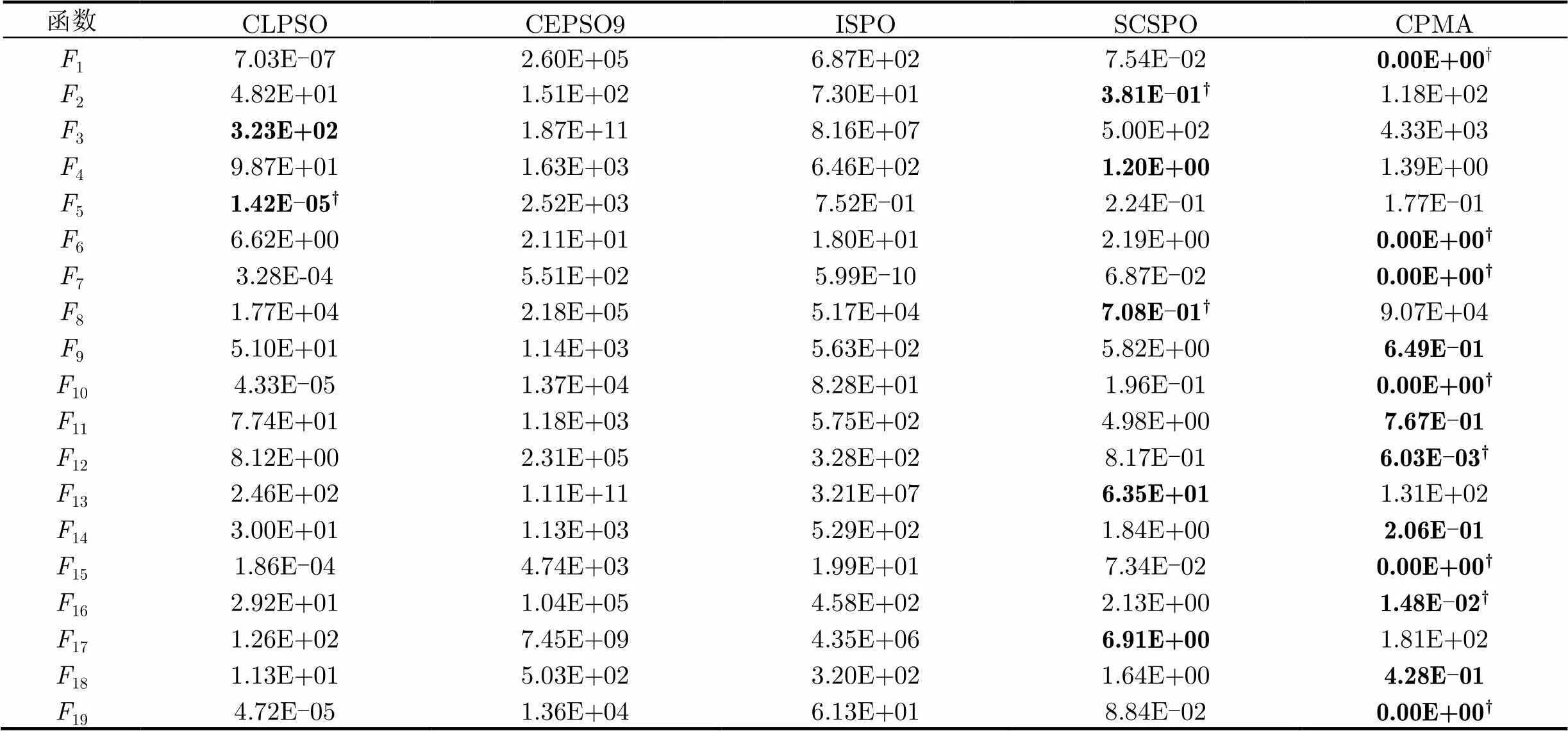
函数CLPSOCEPSO9ISPOSCSPOCPMA F17.03E-072.60E+056.87E+027.54E-020.00E+00† F24.82E+011.51E+027.30E+013.81E-01†1.18E+02 F33.23E+021.87E+118.16E+075.00E+024.33E+03 F49.87E+011.63E+036.46E+021.20E+001.39E+00 F51.42E-05†2.52E+037.52E-012.24E-011.77E-01 F66.62E+002.11E+011.80E+012.19E+000.00E+00† F73.28E-045.51E+025.99E-106.87E-020.00E+00† F81.77E+042.18E+055.17E+047.08E-01†9.07E+04 F95.10E+011.14E+035.63E+025.82E+006.49E-01 F104.33E-051.37E+048.28E+011.96E-010.00E+00† F117.74E+011.18E+035.75E+024.98E+007.67E-01 F128.12E+002.31E+053.28E+028.17E-016.03E-03† F132.46E+021.11E+113.21E+076.35E+011.31E+02 F143.00E+011.13E+035.29E+021.84E+002.06E-01 F151.86E-044.74E+031.99E+017.34E-020.00E+00† F162.92E+011.04E+054.58E+022.13E+001.48E-02† F171.26E+027.45E+094.35E+066.91E+001.81E+02 F181.13E+015.03E+023.20E+021.64E+004.28E-01 F194.72E-051.36E+046.13E+018.84E-020.00E+00†

表5各算法在=500的平均误差值优化结果

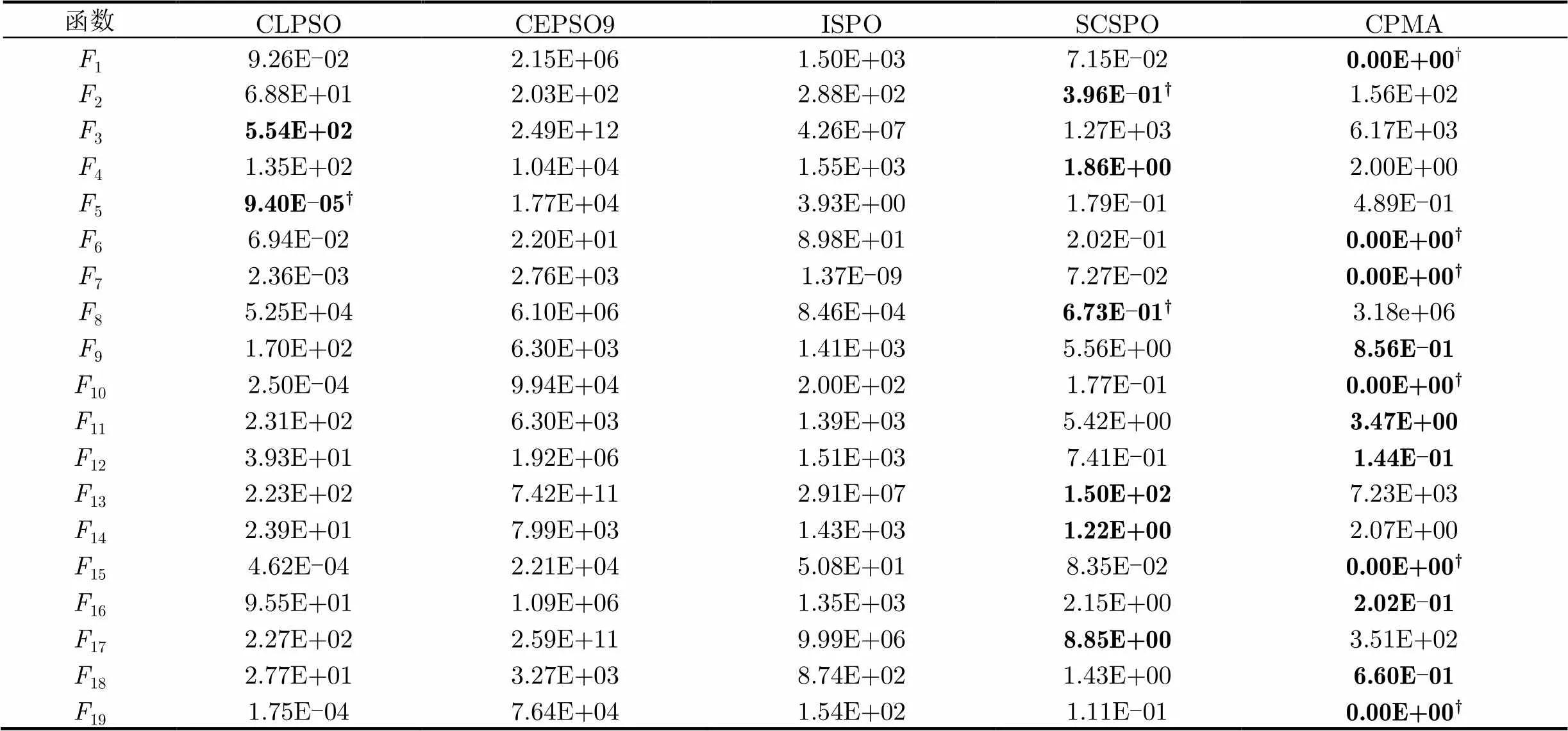
函数CLPSOCEPSO9ISPOSCSPOCPMA F19.26E-022.15E+061.50E+037.15E-020.00E+00† F26.88E+012.03E+022.88E+023.96E-01†1.56E+02 F35.54E+022.49E+124.26E+071.27E+036.17E+03 F41.35E+021.04E+041.55E+031.86E+002.00E+00 F59.40E-05†1.77E+043.93E+001.79E-014.89E-01 F66.94E-022.20E+018.98E+012.02E-010.00E+00† F72.36E-032.76E+031.37E-097.27E-020.00E+00† F85.25E+046.10E+068.46E+046.73E-01†3.18e+06 F91.70E+026.30E+031.41E+035.56E+008.56E-01 F102.50E-049.94E+042.00E+021.77E-010.00E+00† F112.31E+026.30E+031.39E+035.42E+003.47E+00 F123.93E+011.92E+061.51E+037.41E-011.44E-01 F132.23E+027.42E+112.91E+071.50E+027.23E+03 F142.39E+017.99E+031.43E+031.22E+002.07E+00 F154.62E-042.21E+045.08E+018.35E-020.00E+00† F169.55E+011.09E+061.35E+032.15E+002.02E-01 F172.27E+022.59E+119.99E+068.85E+003.51E+02 F182.77E+013.27E+038.74E+021.43E+006.60E-01 F191.75E-047.64E+041.54E+021.11E-010.00E+00†

4.3 DNA基准测序序列

假设5种PSO改进算法对11条DNA基准测序序列优化码书大小均为=8,=32，优化时均执行30次且MaxFEs设置为2×105。实验使用各算法在基准测序序列上的压缩率作为评价指标，并与传统经典DNA序列压缩算法(如Gencompress[2](Gen),DNAcompress[18](DNAc),DNApack[3](DNAp), GeNML[4])进行对比，结果如表6所示。

表6表明，相对于其它压缩算法，本文提出的CPMA算法对DNA基准测序序列的压缩率(BPB)最小。同时5种优化算法与经典的DNA序列数据压缩算法相比，对DNA序列的压缩率得到了提高，并且不同序列的压缩效果也比较稳定。

5 结论

本文提出一种基于Memetic算法的DNA序列数据压缩方法，即CPMA算法。该方法采用CLPSO, DACSO的全局搜索和局部搜索相结合的Memetic算法寻找EARV码书，然后用此码书压缩DNA序列数据。CPMA算法不仅对标准复合测试函数具有较好的优化性能，而且对DNA基准测序序列具有较好的压缩率；同时，相比于经典的DNA序列数据的压缩算法，将优化算法应用于DNA序列压缩，其压缩性能有较大提升。

表6各算法对11条DNA基准测序序列的压缩率比较

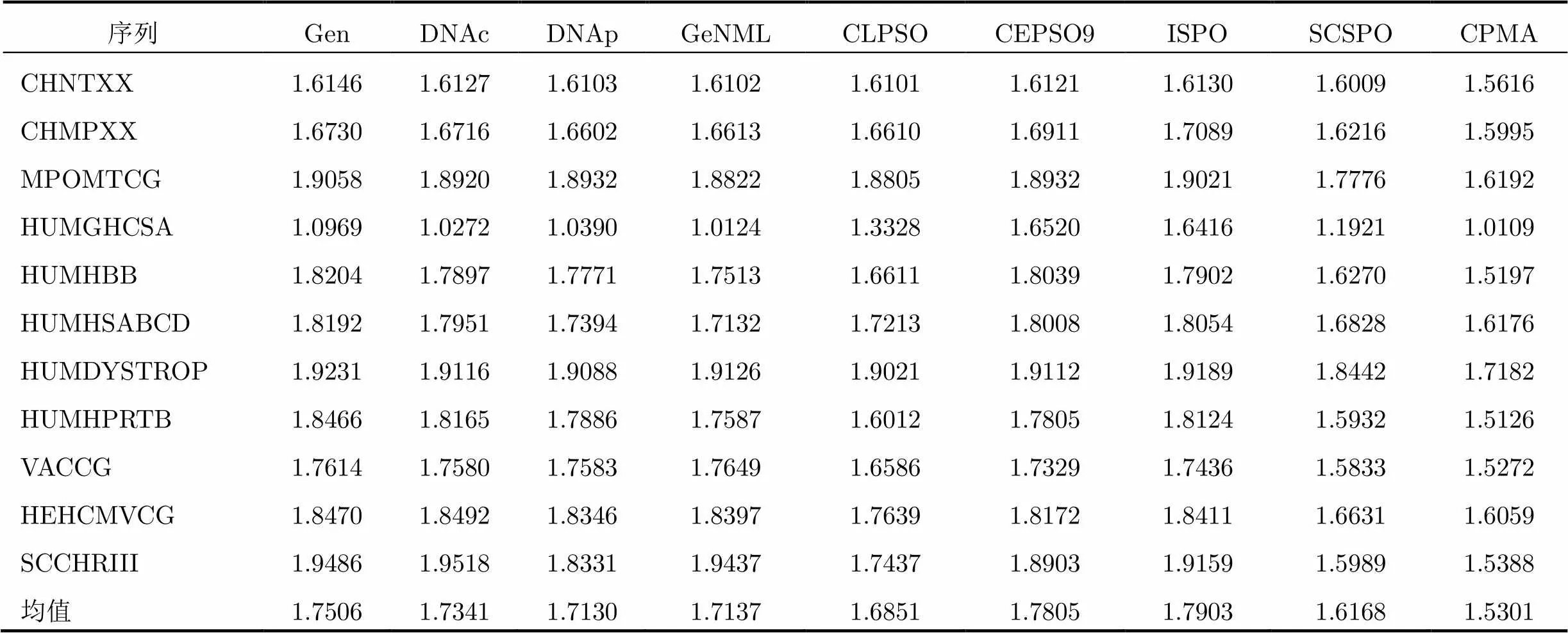
序列GenDNAcDNApGeNMLCLPSOCEPSO9ISPOSCSPOCPMA CHNTXX1.61461.61271.61031.61021.61011.61211.61301.60091.5616 CHMPXX1.67301.67161.66021.66131.66101.69111.70891.62161.5995 MPOMTCG1.90581.89201.89321.88221.88051.89321.90211.77761.6192 HUMGHCSA1.09691.02721.03901.01241.33281.65201.64161.19211.0109 HUMHBB1.82041.78971.77711.75131.66111.80391.79021.62701.5197 HUMHSABCD1.81921.79511.73941.71321.72131.80081.80541.68281.6176 HUMDYSTROP1.92311.91161.90881.91261.90211.91121.91891.84421.7182 HUMHPRTB1.84661.81651.78861.75871.60121.78051.81241.59321.5126 VACCG1.76141.75801.75831.76491.65861.73291.74361.58331.5272 HEHCMVCG1.84701.84921.83461.83971.76391.81721.84111.66311.6059 SCCHRIII1.94861.95181.83311.94371.74371.89031.91591.59891.5388 均值1.75061.73411.71301.71371.68511.78051.79031.61681.5301

[1] Witold K. Towards cognitive analysis of DNA[C]. 2010 9th IEEE International Conference on Cognitive Informations, Beijing, 2010: 6-7.

[2] Chen X, Kwong S, and Li Ming. A compression algorithm for DNA sequences and its applications in genome comparison[C]. Proceedings of the 10th Workshop on Genome Informatics, Tokyo, 1999: 51-61.

[3] Behzadi B and Fessant F L. DNA compression challenge revisited: a dynamic programming approach[C]. Proceedings of the 16th Annual Symposium on Combinatorial Pattern Matching, Jeju Island, 2005: 190-200.

[4] Korodi G and Tabus I. An efficient normalized maximum likelihood algorithm for DNA sequence compression[J]., 2005, 23(1): 3-34.

[5] Chern B G, Ochoa I, Manolakos A,.. Reference based genome compression[C]. 2012 IEEE Information Theory Workshop, Lausanne, 2012: 427-431.

[6] 纪震, 周家锐, 朱泽轩, 等. 基于生物信息学特征的DNA序列数据压缩算法[J]. 电子学报, 2011, 39(5): 991-995.

Ji Zhen, Zhou Jia-rui, Zhu Ze-xuan,.. Bioinformatics features based DNA sequence data compression algorithm[J]., 2011, 39(5): 991-995.

[7] Kamta N M, Anupam A, Edries A,.. An efficient horizontal and vertical method for online DNA sequence compression[J]., 2010, 3(1): 39-46.

[8] Ji Zhen, Zhou Jia-rui, Zhu Ze-xuan,.. Self-configuration single particle optimizer for DNA sequence compression[J]., 2013, 17(4): 675-682.

[9] Liang J J, Qin A K, Suganthan P N,.. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]., 2006, 10(3): 281-295.

[10] Zhu Ze-xuan, Zhou Jia-rui, Ji Zhen,.. DNA sequence compression using adaptive particle swarm optimization- based memetic algorithm[J]., 2011, 15(5): 643-658.

[11] Wang Hong-feng, Moon I K, Yang S,.. A memetic particle swarm optimization algorithm for multimodal optimization problems[J]., 2012, 197: 38-52.

[12] Li Hong-jian, Ni Bing, Wong Man-hon,.. A fast CUDA implementation of agrep algorithm for approximate nucleotide sequence matching[C]. 2011 IEEE 9th Symposium on Application Specific Processors, San Diego, 2011: 74-77.

[13] Long Min and Tan Li. A chaos-based data encryption algorithm for image/video[C]. 2010 2nd International Conference on MultiMedia and Information Technology, Kaifeng, 2010: 172-175.

[14] Bilal Alatas, Erhan Akin, and A Bedri Ozer. Chaos embedded particle swarm optimization algorithms[J]., 2009, 40(4): 1715-1734.

[15] 纪震, 周家锐, 廖惠连, 等. 智能单粒子优化算法[J]. 计算机学报, 2010, 33(3): 556-561.

Ji Zhen, Zhou Jia-rui, Liao Hui-lian,.. A novel intelligent single particle optimizer[J]., 2010, 33(3): 556-561.

[16] Lozano M, Molina D, and Herrera F. Editorial scalability of evolutionary algorithms and other metaheuristics for large-scale continuous optimization problems[J]., 2011, 15(11): 2085-2087.

[17] Benson D A, Karch-Mizrachi I, Lipman D J,.. GenBank[J]., 2011, 39: D32-D37.

[18] Chen X, Li M, Ma B,.. DNACompress: fast and effective DNA sequence compression[J]., 2002, 18(12): 1696-1698.

谭 丽： 女，1984年生，博士生，研究方向为生物信息学、图像与视频处理、计算智能.

孙季丰： 男，1962年生，教授，博士生导师，研究方向为图像与视频处理、自组织通信网.

郭礼华： 男，1978年生，副教授，研究方向为图像理解、图像分析、模式识别.

DNA Sequence Data Compression Method Based on Memetic Algorithm

Tan Li Sun Ji-feng Guo Li-hua

(,,510641,)

A DNA sequence compression method based on Collaborative Particle swarm optimization-based Memetic Algorithm (CPMA) is proposed. CPMA adopts the Comprehensive Learning Particle Swarm Optimization (CLPSO) as the global search and a Dynamic Adjustive Chaotic Search Operator (DACSO) as the local search respectively. In CPMA, it looks for the global optimal code book based on Extended Approximate Repeat Vector (EARV), by which the DNA sequence is compressed. Experimental results demonstrate better performance of HMPSO than the other optimization algorithms, and it is very close to the global optimization point in most of the test functions adopted by the paper. The compression performance of the method based on CPMA is markedly improved compared to many of the classical DNA sequence compression algorithms.

DNA sequence compression; Memetic algorithm; Extended Approximate Repeat Vector (EARV); Particle Swarm Optimization (PSO); Dynamic chaotic local search

中国分类号：TP391

A

1009-5896(2014)01-0121-07

10.3724/SP.J.1146.2013.00303

2013-03-12收到，2013-07-27改回

国家自然科学基金(60902087)和广州市科委新星计划项目(2010A 090100016)资助课题

谭丽 t.li07@mail.scut.edu.cn