混合智能算法求解多连接查询优化问题
潘 敏 吴 钊,朱 莉
混合智能算法求解多连接查询优化问题
潘 敏1,2吴 钊1,朱 莉2
(1.湖北文理学院 数学与计算机科学学院,湖北 襄阳 441053;2.中国地质大学 计算机学院,湖北 武汉 430074)
由于数据库多连接查询优化问题类似于经典TSP问题,因此文章采用TSP模型进行多连接查询优化,利用遗传算法进行搜索得到初步较优解空间,并用蚂蚁信息素初始化,然后进行蚁群算法搜索得到整个空间的最优解. 通过仿真实验从时间复杂性和解质量两个方面进行对比分析,验证本混合智能算法在数据库多连接查询优化中具有更好的优化效果.
混合智能算法;多连接查询;遗传算法;查询优化
经过众多学者的研究,最后发现遗传算法有自适应、自组织和自主学习性,并且具有快速全局搜索能力等优点[1]. 但是现有的用遗传算法进行查询优化技术存在局部搜索能力弱,容易陷入局部最优,即早熟收敛[2]. 蚁群算法有很强的鲁棒性,每个蚂蚁可以独立的寻找最优解,因此比较容易用并行实现,它还比较容易与其他的智能算法结合从而提高算法的效率[3]. 但是如果相关参数设置不好,搜索解的效率会很低,另外它的计算量比较大,在刚开始的时候信息素匮乏,导致收敛速度慢,不利于最优解的快速形成[4]. 本文旨在通过深入研究和探讨遗传算法和蚁群算法的不同特性,针对数据库多连接查询优化这一组合优化问题引入一种混合智能算法,以进一步提高数据库多连接查询的效率.
1 多连接查询优化技术
一个给定的查询语句经过选择、投影操作并且通过优化以后得到由数据库中基本关系表连接成的关系代数表达式就称为多连接查询[5]. 随着数据库在应用上有了不断的新拓展,新型的数据库应用需求对查询优化提出了新的要求和挑战.
得到一个最优的查询执行计划(Query Execution Plan,QEP)是多连接查询优化的核心. 数据库多连接查询优化问题和经典的TSP问题非常类似[6],可以把数据库中的基本关系表看作城市,把两个连接关系的代价花费看作两个城市之间的开销. 从而可以把多连接查询优化问题用TSP模型进行优化,而且智能算法在解决TSP问题时取得很好的效果[7].
1.1 多连接查询的表示方法
数据库多连接查询优化就是,从所有的查询执行计划集合中去寻找一个效率最好的一个执行计划. 在这个优化过程中它需要用到多种查询表示方法. 对于一个给定的查询语句,通过语法分析、词法分析以及语义确认,然后用查询图形式表示,在查询优化器优化以后,生成的关系代数表达式会用连接树进行表示,最后经过物理优化的最佳查询执行计划,它会用操作树进行表示.
1) 查询图:在数据库多连接查询中,一个连接查询图可以表示为=(,),基本关系表代表结点,并且,边(1,2)代表两个表的连接类型,数据库表连接类型可以分为外连接、内连接和交叉连接. 比如数据库多连接查(1,2)and(1,3)and(2,4)的查询图如图1所示.

图1 查询图
2) 连接树:查询图的每一个可能的查询计划通过连接树来表示,叶子节点表示数据库中的关系,中间节点对应左、右节点联结的结果集. 图2(a、b、c)描述了三种不同的查询执行计划.
3) 操作树:逻辑关系代数通过物理优化以后,可以获得多连接的物理操作顺序,查询优化器一般采用操作树的表示方法. 图3为左深树(图2(a))经过物理优化得到一个操作树.
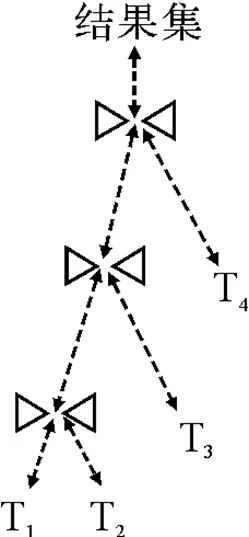
图2(a) 左深树
图2(b) 右深树
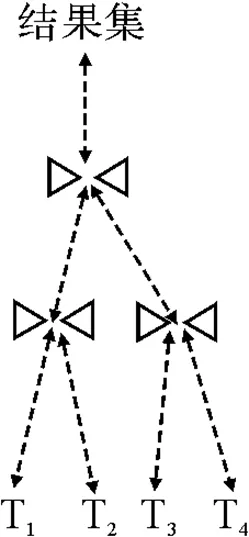
图2(b) 右深树
1.2 代价评估模型
目前的数据库系统中一般都存在数据量庞大、数据模型复杂、关系记录数量庞大等特点,所以在进行连接操作的时候,要处理的数据就要分批输入内存中,这样就会产生大量的输入输出开销,然而在内存中计算的代价相对于输入输出开销是比较小的. 为了方便对多连接查询优化中执行计划的代价估算[8],一般只会考虑输入输出开销. 本文采用了一个简单的估算执行计划开销的模型,这个模型成立的条件:一是基本关系表的属性值分布要均匀;二是执行连接操作后的结果集里面的元组数的规模对执行计划的开销起决定性作用.
数据库的数据字典中会保存一些基本表的统计信息,比如以下的统计信息是在估算执行计划代价过程要用的:()指的是基本关系表中元组的数量,也叫这个关系表的基数.(,)指的是在基本关系表中属性的不同值的数量.
那么,对于一个包含个基本关系表的连接树,(1,T,T,,T)为这个树非叶子结点,其开销评估模型为:
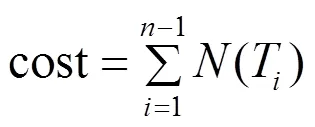
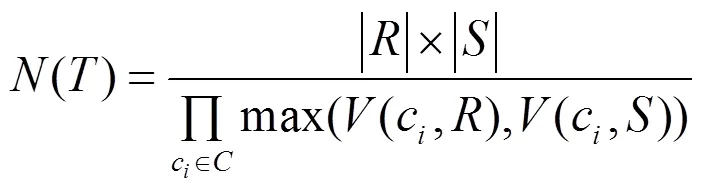
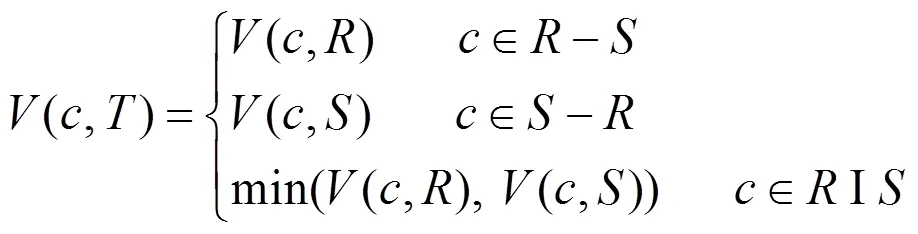
2 基于遗传蚁群混合算法的多连接查询优化
2.1 遗传蚁群混合算法设计
遗传蚁群混合算法设计的基本思想是:先用遗传算法开始全局较优解搜索,经过一定代数的选择算子、交叉算子和变异算子等操作的优化搜索,不断得到比较优良的解. 然后再对这些解的连接顺序进行信息素生成,用蚁群算法对这些种群进行搜索优化,这就解决了蚁群算法开始时信息素缺乏导致搜索速度慢的问题. 该混合算法对数据库多连接查询优化流程图如图4所示.
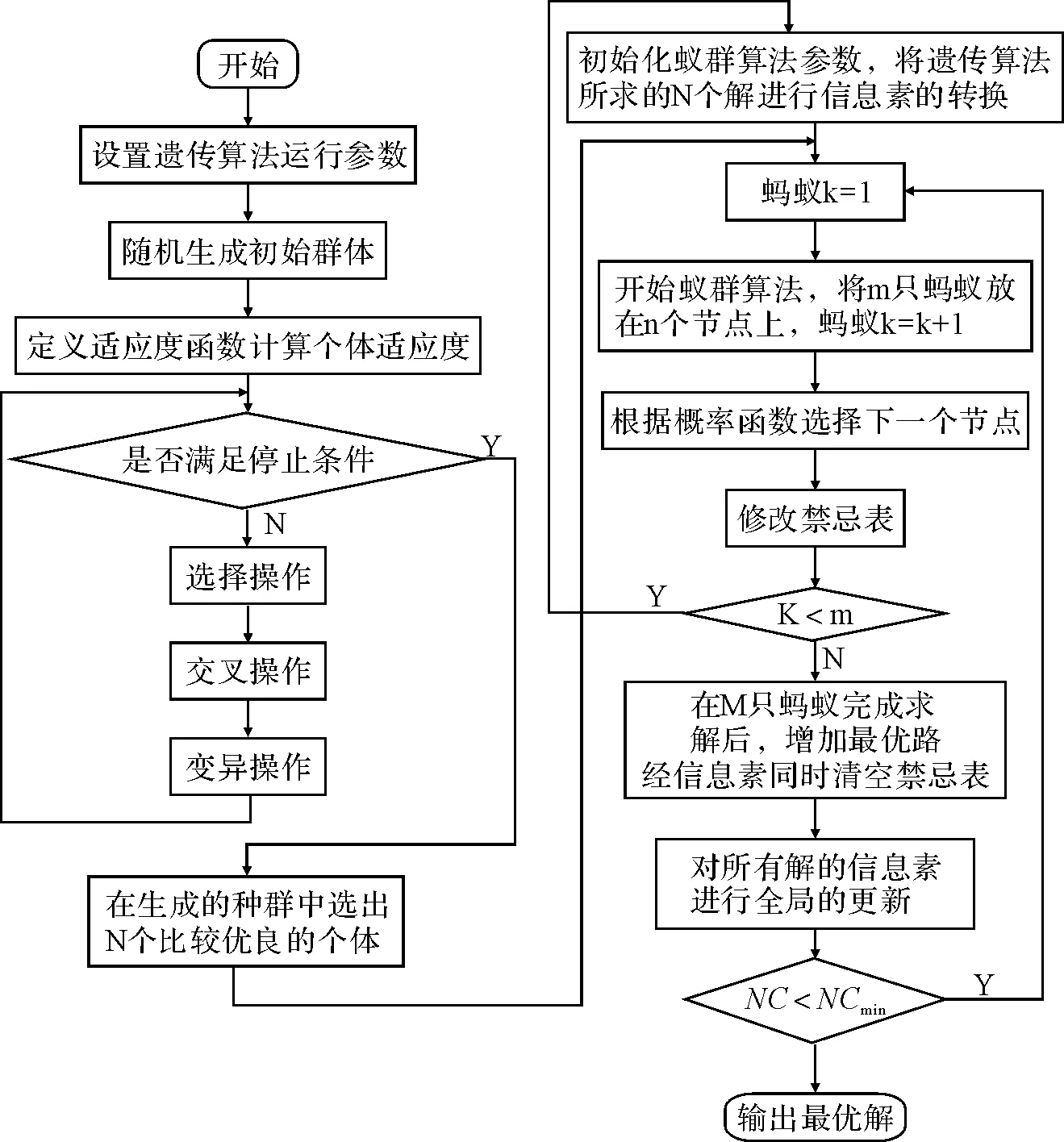
图4 混合算法流程图
2.2 混合算法的多连接查询优化的实现
2.2.1编码方案
由于基于左深树的数据库多连接查询问题与TSP问题存在很大的相似性,一个连接关系的序列与左深树可以一一对应,因此可以采用关系序列进行编码. 首先对要处理的个关系,用自然数进行编码,然后不同的左深树按照后根遍历的方式进行读取关系的序号形成编码,这样就生成一条染色体. 可以明显看出,针对个关系的多连接查询优化,那么染色体的长度也就是. 如图5中一个左深树,它的染色体编码是(2,1,4,3),它的编码长度是4.
图5 左深树
2.2.2初始种群生成
首先程序会随机生成一个染色体编码,然后会对生成的这个染色体进行判断是否包含了笛卡尔积,如果含有笛卡尔积那么就会淘汰这个初始化个体,把不包含笛卡尔积的个体加入到初始化种群中,直到初始化种群的个体数目满足设定的参数为止. 针对一个给定的查询,假设它的查询图为,在这个查询图中包含了个关系的操作,则可以按照下面的步骤进行处理:
1)每个基本表连接关系组成子图,这些子图共同构成查询子图的集合;
2)把每个基本表关系看成叶子结点,连接的操作看成根节点,这样的话每个连接子图就形成了一棵树,就形成了森林;
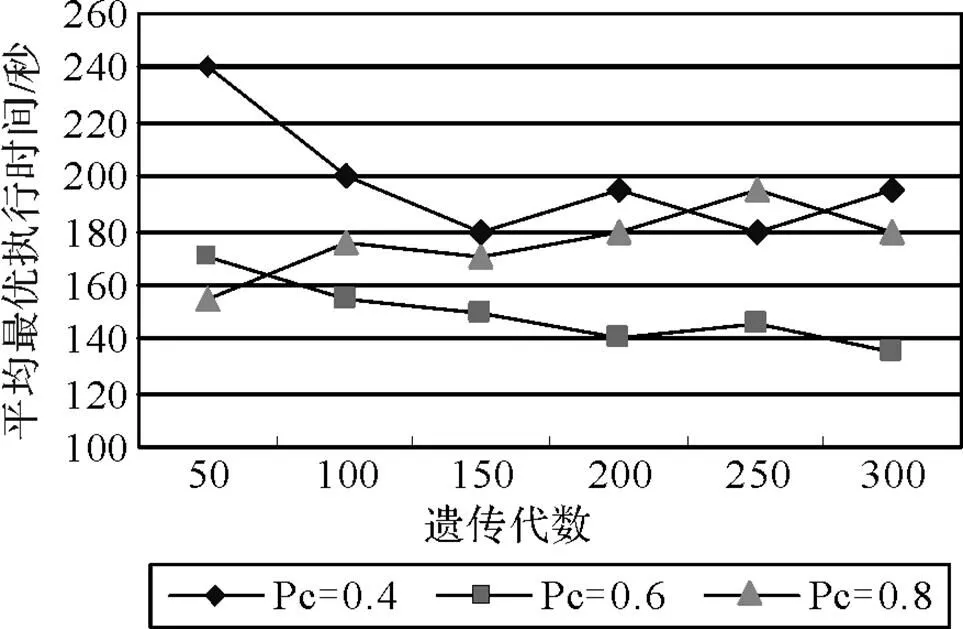
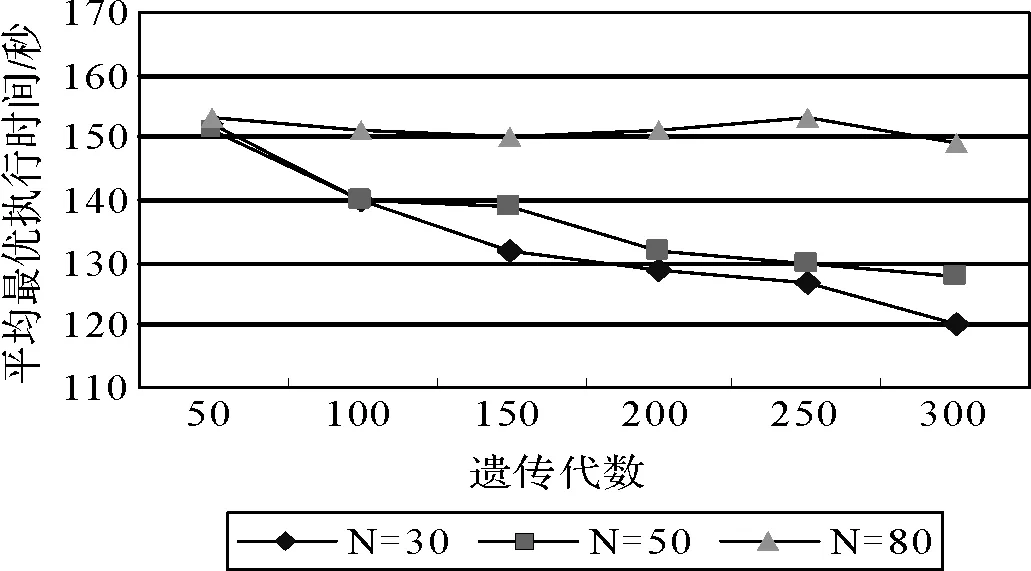
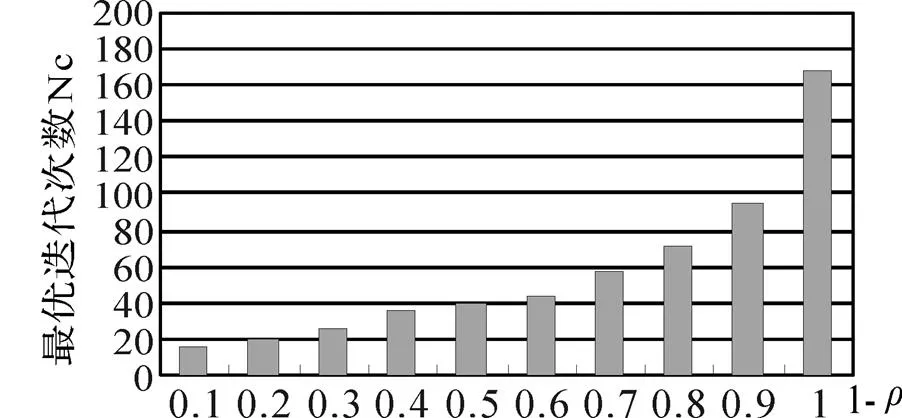
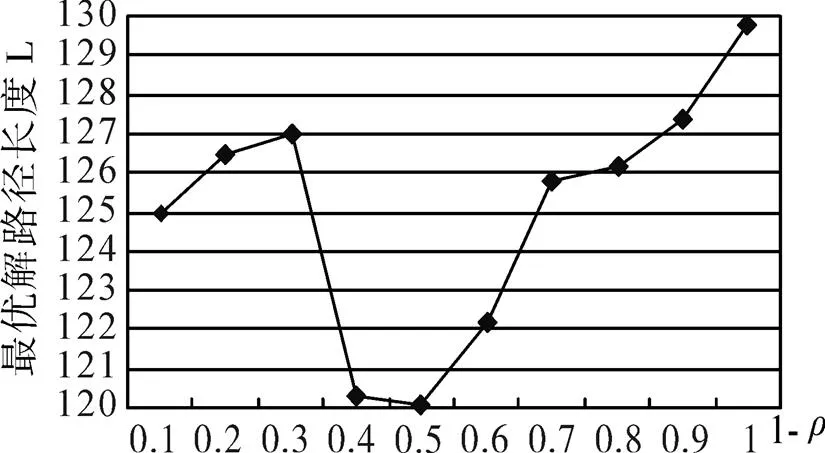
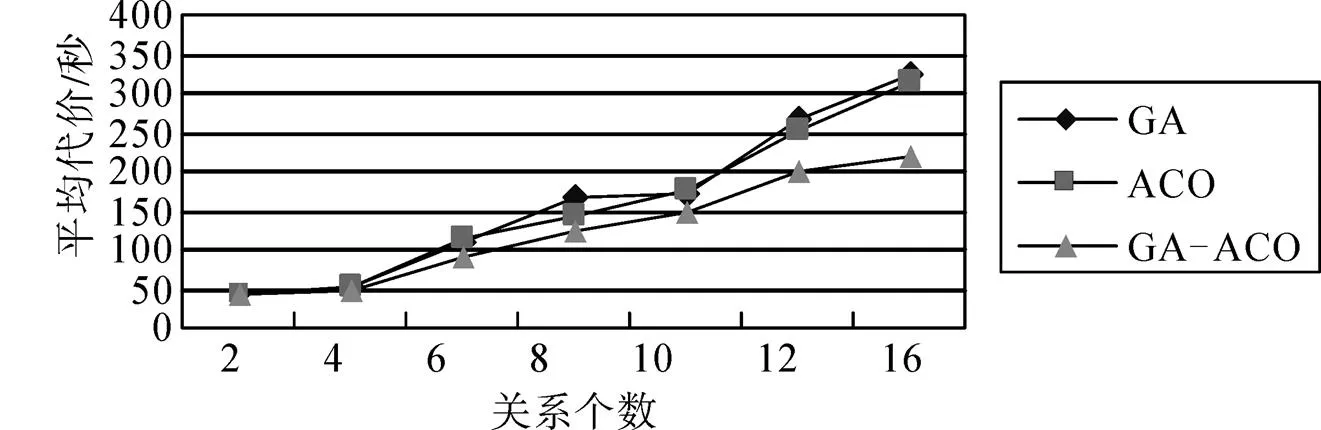
for(i=1;i { While(||>1) { 从森林中随机选择一个子图; 按照查询图,寻找与这个子图连接的子图; 在中选择与这两个子图相符合的树,由他们两个分别作为左右子树生成一个新的树; 把这棵新生成的树加入,并删除原来的那两棵树; } 后根遍历由形成的树,从而得到一个染色体序列也就是一个个体; 把这个个体加入到初始种群中; } 2.2.3适应度函数 根据一般数据库多连接查询优化遗传算法的设计,这里取适应度函数为 2.2.4确定遗传算子 选择策略:采用精英个体保留和基于正态分布的混合选择策略. 精英个体保留策略就是对当前种群中适应度值最小的连接树不进行交叉、变异操作,淘汰适应度值大的连接树. 这种选择策略保证了当前优良的个体不会被进化操作破坏掉,有利于保证算法的收敛性. 交叉策略:遗传算法部分交叉算子采用循环杂交交叉算法,对每个新个体进行包含笛卡尔积检验,从而判断是否舍弃两个个体交叉生成的后代. 变异策略:在选中要进行变异的个体中随机选择两个基因,把两个基因交换从而形成新的个体. 2.2.5遗传解转换为蚁群的信息素 遗传算法进化到设置的代数,然后把遗传算法得到的解进行信息素转换. 本文蚁群算法的初始化群体是利用遗传算法得到的,把蚁群算法的信息素初值设置成μ=μ+μ,其中μ是按照不同问题给出的一个不同信息素常数(本文取为0.001),μ是把遗传算法得到的最优解转化的信息素值. 具体转换策略:首先,把遗传算法得到的优化个体按照适应度值按照从大到小进行排序;为了更好的利用到遗传算法得到解的信息,同时要避免得到局部最优解,选取适应度值高的前90%的个体加上随机产生的10%的个体产生新的矩阵. 然后,计算中每两个基本表连接关系(R,R)出现的次数K,将K/作为蚁群算法初始信息素μ的值,其中代表的是初始种群的数量. 如果两个连接没出现在这些较优解中的话,那么它们对应的信息素值为0. 2.2.6蚁群算法参数初始化 蚁群算法的一些参数对算法的效率影响比较大[9],为了得到最佳的参数组合,采用步骤:1)确定蚂蚁的数量当基本表关系数量/蚂蚁的数量约等于1.5时才确定蚂蚁的数目. 2)参数的初步估计 对信息启发系数、期望因子、信息素挥发因子、信息素强度进行较大取值范围的调整. 每个连接的信息素已经利用遗传算法的解转化得到,以便得到更优的解. 3)参数的微小调整 对信息启发系数、期望因子、信息素挥发因子、信息素强度进行较小取值范围的调整. 4)重复以上操作 直到选出一组比较理想的参数为止. 2.2.7蚁群算法的状态转移规则设置 蚂蚁在找寻最优路径的时候,它们是通过状态转移的概率来进行选择下一个表关系,而这个状态转移概率是通过路径中信息素的浓度和路径启发函数来计算得到的,其公式如下: 其中,L={-S},代表的是第个蚂蚁在当前时刻可以选择的城市集合.为信息素启发因子,主要是反映蚂蚁在选择路径的时候,信息素对它的选择的重要程度,值越大,那么蚂蚁就越容易选择信息素高的路径.代表期望因子,主要反映的是蚂蚁在选择路径的时候,能见度对其进行路径选择的影响程度,值越大,蚂蚁在选择路径的时候就越容易用贪心策略进行选择下一个城市.f表示的是能见度算子, f=1/d. 其中,代表的是信息素的浓度,它的值的设定与算法的收敛速度有一定的影响;W代表的是当前迭代中第只蚂蚁所经过基本表连接关系的总代价. 本文实验分为两个部分,首先是研究与算法相关参数对算法的影响,从而选择比较合适的参数组合. 其次是通过单纯的遗传算法和蚁群算法与混合算法在不同连接关系个数的情况下的优化效果比较,检验混合算法有更好的优化效果. 图6呈现的是在不同交叉率的时候,算法所表现出的性能情况. 可以从其中看出,当Pc=0.4的时候,算法收敛的速度比较快,最优解也比较的好;当Pc=0.8的时候,算法收敛比较慢;当Pc=0.6的时候,不管是从收敛速度还是从最优解的均值都比其他两种情况要好,因此本文采用交叉率为0.6. 图7表现出来的是在不同种群规模的情况下,算法所表现出来的性能情况. 一般情况下,种群规模N越小,越有利于遗传算法速度的提高,但是这样却降低了种群的多样性,这会引起算法的过早收敛,你利于搜索全局更好的解;当种群规模N比较大的时候,加大了算法的计算量,从而降低了效率,但是这样却提高搜索到全局最优解的可能性. 从图中可以看出种群规模取30是一个合适的选择. 图6 不同交叉概率 图7 不同种群大小 仿真实验的样本数据是包含12个基本表关系的多连接查询请求. 通过多次的仿真实验和数据分析,得到了1与进化代数和最优解路径长度之间的关系,分别可以通过图8和9看出. 最优解迭代次数随着1-的增大而增大,如果1-的值较大的时候,信息素会主导蚂蚁寻找最优解的过程,蚂蚁搜索的随机性会增加,从而减缓算法的收敛速度. 如果1-的值较小的时候,降低了搜索的随机性,有利于算法迅速收敛,但是也容易陷入局部最优解. 根据图中可以看出,当1-的值取0.5的时候算法不管从收敛速度和最优解的质量都比较好. 图8 Nc与1-ρ的关系 图9 路径长度与1-ρ的关系 根据参数比较优的组合对不同算法多连接查询优化的效果进行分析可以得出:当关系数目较小的时候他们的优化效果差别不大,但是当优化的关系数目大的时候就会出现较为明显的差别. 如图10,可以看出:如果查询涉及的关系个数比较少的时候,这几种算法的优化效果没有太大的区别,但是当关系的个数超过4个的时候,混合算法的优化效果明显好于单纯一种算法的优化效果. 图10 不同算法平均代价的对比 本文简要分析了数据库多连接查询优化问题,并给出了解决这个问题的混合智能算法的实现步骤. 把左深树空间作为搜索空间,对连接的顺序进行编码,先通过遗传算法进行优化,然后把优化后的结果进行信息素的转化,再通过蚁群算法进行优化,通过仿真实验分析算法的初始化参数对算法效果的影响,并验证混合智能算法相对于单纯遗传、蚁群算法的高效性. 本文提出混合遗传蚁群算法进行数据库多连接查询优化,虽然取得了比较好的优化效果,但是对于本文混合算法后半阶段,蚁群算法本身还有较多方面可以进一步完善比如:局部搜索策略的选择,相关参数的设定. [1] DONG HONGBIN, LIANG YIWEN. Genetic Algorithm for Large Join Query Optimization[C]//Genetic And Evolutionary Computation Conference. Proceedings of the 9th annual conference on Genetic and Evolutionary computation. New York: Association for Computing Machinery, 2007: 1211-1218. [2] 冯亚丽, 刘 阳, 赵艳玲, 等. 基于遗传算法的数据库多连接查询优化策略[J]. 佳木斯大学学报: 自然科学版, 2007, 25(4): 506-508. [3] 王 玥, 陶洪久. 蚁群优化算法在TSP中的应用[J]. 武汉理工大学学报: 信息与管理工程版, 2006, 28(11): 24-26. [4] 郭聪莉, 朱 莉, 李 向. 基于蚁群算法的多连接查询优化方法[J]. 计算机工程, 2009, 35(10): 173-175. [5] 闫晓慧, 董丽丽, 张慧娜. 基于混合遗传算法的关系数据库多连接查询优化策略[J]. 微电子学与计算机, 2008, 25(11):182-184. [6] 薛瑞红, 李 扬. 一种改进的蚁群算法及其在TSP问题中的检验[J]. 科技创新导报, 2007, 36: 210-211. [7] 徐金荣, 李 允, 刘海涛, 等. 一种求解TSP的混合遗传蚁群算法[J]. 计算机应用, 2008, 28(8): 2084-2087. [8] 赵 鹏, 王守军, 龚 云. 基于改进蚁群算法的数据仓库多连接查询优化[J]. 计算机工程, 2012, 38(1): 168-172. [9] 徐红梅, 陈义保. 蚁群算法中参数设置的研究[J]. 山东理工大学学报: 自然科学版, 2008, 22(1): 7-9. Multi-connection Query Optimization Based on Hybrid Intelligent Algorithm PAN Min1, 2, WU Zhao1, ZHU Li2 (1. College of Mathematical and Computer Sciences, Hubei University of Arts and Science, Xiangyang 441053, China; 2. School of Computer Science and Technology, China University of Geosciences, Wuhan 430074, China) Problems of multi-connection query optimization based on hybrid intelligent algorithmis similar to the ones of classical TSP. Via the TSP model, it uses genetic algorithm to search for a preliminary better solution space of the problem, initializing the solutions above with the ant pheromone, then obtaining the optimal solutions of the whole space by ant colony algorithm. Comparing and analyzing the time complexity and solution quality, to verify the better optimization results with the hybrid intelligent algorithm. Hybrid intelligent algorithm; Multi-connection query; Genetic algorithm; Query optimization TP301.6 A 2095-4476(2014)05-0015-06 2014-03-04; 2014-3-31 国家自然科学基金项目(61172084); 湖北省自然科学基金项目(2012FFB06411,2012FFB01901, 2013CFC026); 湖北省科技支撑计划项目(2013BHE022) 潘 敏(1988— ), 男, 湖北武汉人, 湖北文理学院与中国地质大学(武汉)联合培养硕士研究生; 吴 钊(1973— ), 男, 湖北武汉人, 湖北文理学院数学与计算机科学学院副教授, 博士, 中国地质大学(武汉)兼职硕士生导师,主要研究方向: 智能算法, 云计算. (责任编辑:饶 超)
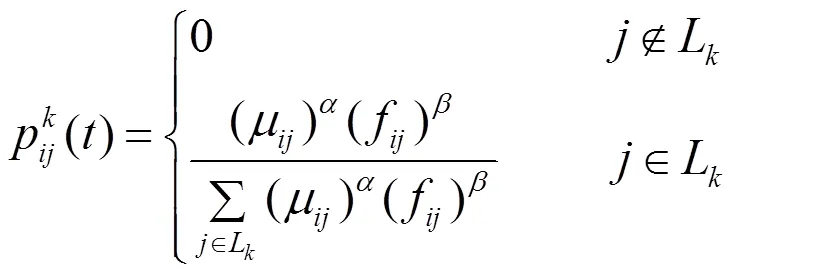
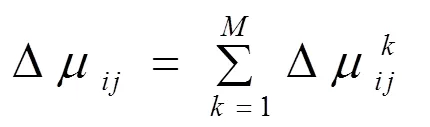

3 仿真实验与结果分析
4 结论

