基于二维电势的超短沟道MOSFET亚阈值电流模型
韩名君,李长波,钱 峰,陶玉贵
1.芜湖职业技术学院信息工程学院,安徽芜湖,241000;2.安徽大学电子信息工程学院,安徽合肥,230601
随着世界上半导体制造工艺的进步,半导体器件的尺寸也是越来越小[1];我国的半导体技术也在飞速发展,目前国内的集成电路设计主要是着眼于65nm、45nm工艺。因此,集成电路设计人员迫切需要简单而又有较高精确度的模型。而随着器件的缩小,亚阈值电流极大地影响了器件的工作特性,这方面已经成为科研人员研究的一个重点方向。目前的MOSFET电流模型研究主要分为两大类:一类是从电荷出发,根据经典的薄层电荷模型、耗尽层近似等得到相应的电流模型,此类模型在计算时均要计算一个包含电势的指数函数的积分,而过去的电势计算多是一维模型或者是准二维模型[2-4],非常便于计算但是精确度不高,当沟道长度缩小到纳米级别时,误差经计算约为20%,因而不再适用于超短沟道情况;另一类模型是考虑器件的量子效应,得到带有量子效应修正量的电流模型[5],该类模型计算简单,但是包含的修正量难以理解、难以测定,给设计人员带来很大的麻烦,同时精确度也得不到保证。
基于以上分析,本文研究一种基于精确的二维电势模型算法上的亚阈值电流模型,给出了包含二维电势的指数函数积分的计算方法,并同时考虑了热电子发射电流,最终得到了超短沟道亚阈值电流模型。通过与Medici[6]仿真结果比较,本文提出的模型能够精确模拟亚阈值下的25~45nm MOSFET器件电流特性。
1 二维电势模型
在亚阈值下,考虑如图1所示衬底为均匀掺杂的NMOSFET模型,图中Ⅰ区为SiO2区域,Ⅱ区位于沟道内的耗尽层区域,Ⅰ区电势ψΙ(x,y)满足拉普拉斯方程及其边界条件。

图1 MOSFETs坐标图
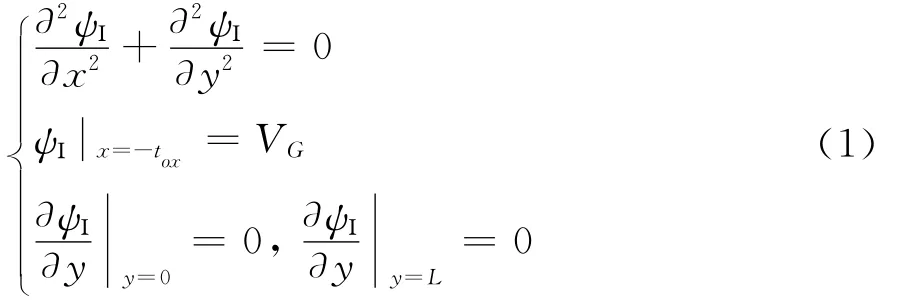
氧化层电势ψΙ(x,y)和耗尽层电势ψⅡ(x,y)之间的边界条件是:

式中,q为电子电量,εsi和εr对应为硅和氧化层的介质常,tox为氧化层厚度,L表示沟道长度,QS为界面电荷。令图1中的栅极电势为禁带宽度,源极电势,漏极电势Vds=Vd+,Vg、Vs和Vd分别为栅源、源极、漏极外加电压,衬底电势VB=-,ni为本征载流子浓度。
在耗尽层区域,MOSFET在亚阈值区可以忽略载流子的影响,这样器件的耗尽层内只有固定离化电荷。令0~d的区域为Ⅱ区,引入矩形等效源,得到耗尽层区域ψⅡ(x,y)的定解问题是:

在耗尽层底部有电势能极值点,满足条件:

根据文献[8]提出的半解析法求解式(1)~(4),得到超短沟道下的二维电势解析模型为:
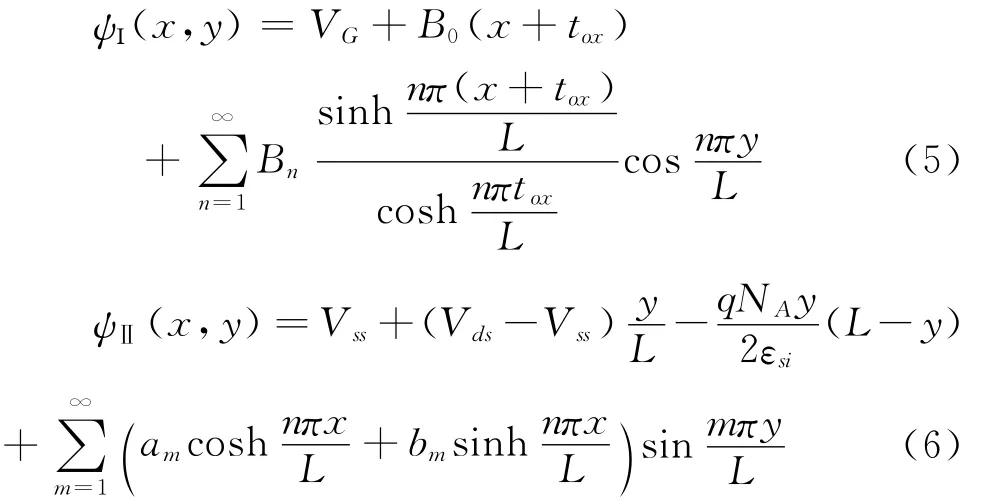
其中的系数B0、Bn和am、bm、cm、dm为未知常数,用半解析法计算。
由此得到表面势模型为:
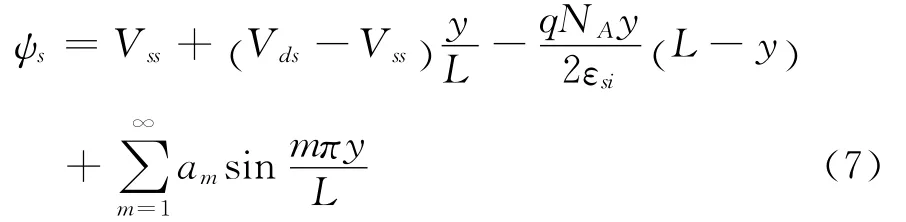
2 亚阈值电流模型
根据文献[4],亚阈值漏电流的经典表达式为:

其中等效耗尽层厚度为:

由于其中的阈值电压Vth为未知量,可以将其设为Vth=ηφf,φf=,η为适配参数,经典的长沟道阈值电压定义为Vth=2φf,η取2,而对超短沟道下的阈值电压,由于DIBL效应和短沟效应等效应的影响η<2,经仿真拟合可以取η≈1.8。
式(8)中的φs(0)和φs(L)则分别是源端和漏端电势,根据图1的MOSFET模型坐标有φs(0)=Vss和φs(L)=Vds,W则是器件宽度,热电压为载流子迁移率。
式(6)中的φs(y)如果直接用于求解亚阈值电流非常困难,因此本文提出采用将φs()y的求和项用最佳平方逼近法去逼近,设:

定义函数:

并对f(y)的平方项f(y)2作积分,得到:

将I分别对p0、p1和p2求导,并使求导结果为零,可以得到方程组:
计算解得p0、p1和p2,代入φs()y后可以将φs()y可以化简为:

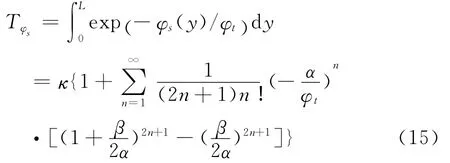
最后得到漏电流计算式为:

此为基于精确的二维电势模型基础上给出的亚阈值电流计算模型,适用于长沟道情况下。
随着沟道长度的缩短,单纯的计算式(16)而忽略热电子发射电流,得到的结果与实际误差较大,因此热电子发射电流Ite不可忽略。当漏极偏置电压为零时,热电子发射电流为零;而当漏极偏置电压逐渐增大时,此时的漏电流很大程度上取决于器件的热电子发射电流,热电子发射电流定义为:

其中,I0=WδA*T2,A*为 Richardson常数,具体计算时为:

其中,A*0=1.0×106,L0=50nm。
这样,对于超短沟道MOSFET器件,亚阈值电流模型为漏电流和热电子发射电流的并联:

3 模型验证
为了验证模型的正确性,将电流模型计算值与Medici模拟结果对比分析,栅氧化层厚度取2nm,界面电荷密度QS=1e10cm-2。源、漏结中的掺杂浓度ND=2e20cm-3,其余工艺参数则在参考国际半导体工艺路线图(ITRS)的基础上具体给定。
图2为不同沟道长度下的亚阈值电流对数特性曲线,沟道长度L分别取25nm、30nm和35nm,漏电压Vd=0.2V。由图可见,本文模型可以得到超短沟道情况下的精确亚阈值电流值。在计算中,发现随着沟道长度的缩短,热电子电流增大,而随着工艺的发展,沟道长度还在急剧缩短,因此,本文模型对预测40nm以下的沟道长度电流具有指导意义。
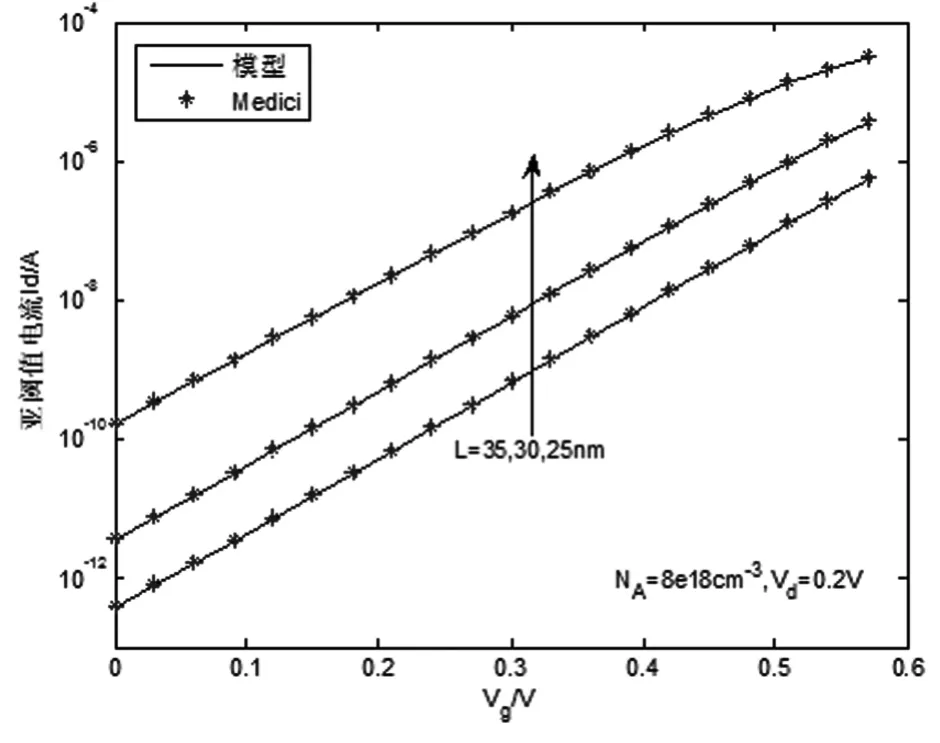
图2 亚阈值电流随L变化的曲线
图3为不同漏极偏置电压Vd下的亚阈值电流对数特性曲线,沟道长度取45nm,Vd从0.1V变化到1V,从图中可以看出,在亚阈值情况下,本文模型与MEDICI结果吻合,误差小于6%,因此该模型可以准确预测漏致势垒降低(DIBL)效应对亚阈值电流的影响。

图3 亚阈值电流随Vd变化的曲线
图4为不同沟道掺杂浓度NA下的亚阈值电流对数特性曲线,此处的沟道长度取35nm,NA则从NA变化到NA。由图可见,本文模型同样可以精确模拟掺杂浓度对器件亚阈值电流的影响。
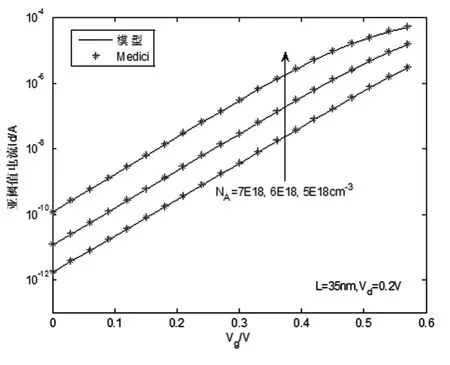
图4 亚阈值电流随NA变化的曲线
4 结 论
本文提出了基于精确的二维电势模型的亚阈值电流的计算方法,同时考虑了热电子发射电流,最终得到了超短沟道亚阈值电流模型。通过与Medici仿真结果比较表明,在不同的沟道长度、偏置电压和掺杂浓度下,该电流模型均能够精确模拟亚阈值下的25~45nm MOSFET器件电流特性。该算法同样可以运用于其他不同结构的MOSFET器件模型。
[1]ITRS.2011Technology Working Group Reports[EB/OL].[2014-01-10].http://www.itrs.net/Links/2011ITRS/Home2011.htm,2012-01-20/2013-07-16
[2]Xie Q,Xu Jnm,Yuan Taur.Review and critique of analytic models of MOSFET short-channel effects in subthreshold[J].IEEE Trans ED,2012,59(6):1569-1579
[3]D J Frank,Y Taur,H-S P Wong.Generalized scale length for two dimensional effects in MOSFETs[J].IEEE ED Lett,1998,19(10):385-387
[4]S Baishya,A Allik,C K Sarkar.A subthreshold surface potential model for short-channel MOSFET taking into account the varying depth of channel deplation layer due to source and drain junction[J].IEEE Trans ED,2006,53(3):507-514
[5]G S Jayadeva,Amitava DasGupta.Analytical Approximation for the Surface Potential in n-Channel MOSFETs Considering Potential in n-Channel MOSFETs Considering[J].IEEE Trans ED,2010,57(8):1820-1828
[6]MEDICI version A user guide[D].California,UC:Synopsys Company,2007
[7]T Toyabe,S Asai.Analytical models of threshold voltage and breakdown voltage of short-channel MOSFETs derived from two-dimensional analysis[J].IEEE Trans ED,1979,26(4):453-461
[8]韩名君,柯导明.超短沟道MOSFET电势的二维半解析模型[J].物理学报,2013,62(9):098502

