亚临界雷诺数下圆柱和方柱绕流数值模拟

沈立龙，刘明维，吴林键，李鹏飞，舒 丹

（重庆交通大学国家内河航道整治工程技术研究中心，水利水运工程教育部重点实验室，重庆 400074；重庆交通大学河海学院，重庆 400074）

亚临界雷诺数下圆柱和方柱绕流数值模拟

沈立龙，刘明维，吴林键，李鹏飞，舒 丹

（重庆交通大学国家内河航道整治工程技术研究中心，水利水运工程教育部重点实验室，重庆 400074；重庆交通大学河海学院，重庆 400074）

基于RNG k⁃ε模型，采用有限体积法对亚临界雷诺数条件下（Re=3×102～3×105）的二维单圆柱和单方柱绕流进行数值模拟与仿真。得到了圆柱和方柱绕流阻力系数Cd与Strouhal数随雷诺数的变化规律。同时对雷诺数Re=22 000下的圆柱、方柱绕流相关特性进行详细对比分析。计算结果表明：同一雷诺数下，单圆柱绕流阻力系数Cd较单方柱低，但圆柱的Strouhal数较单方柱则要高。虽然二者边界层分离点不同，但流场的演变与漩涡的脱落具有一定相似特性。

亚临界雷诺数；圆柱和方柱；绕流；数值模拟；RNGk⁃ε模型

Biography：SHEN Li⁃long（1990-）,male,master student.

钝体绕流现象普遍存在于实际生活中，如桥墩绕流，深海输油立管绕流，飞机机翼绕流，化学反应塔绕流等。绕过钝体的流体流动极不稳定，周围的流场也变得，当涡街发生时，交替产生并脱落的漩涡诱发交变力，使得被绕流的物体产生振动及噪声，严重时产生共振及声振，对建筑物正常使用安全造成了极大的威胁。由此，钝体绕流问题现已成为流体力学领域所研究热点问题之一。国内外学者对此进行了大量的模拟研究，Standsby等人［1］采用随机涡法对放置方法不同的串列、并排双圆柱进行了数值分析，得到结果与实验基本相符；苏明德等人［2］采用二阶精度有限体积法和Smagorinsky涡粘性模式对雷诺数Re为200和20 000下的圆柱绕流进行了大涡模拟，同样得到了与实验结果相近的升、阻力系数等动力学参数；Kawai Hiromasa等人［3］采用差分法对雷诺数Re为200的串列方柱的绕流做了数值模拟；王远成等人［4］采用湍流RNGk⁃ε模型对方柱绕流流场的相关特性进行了数值模拟，很好的反映出了漩涡脱落的尾迹结构。

桩柱的绕流受到边界条件、湍流强度、柱面粗糙度等因素的影响［5］，但起决定作用的是雷诺数。随着雷诺数的增加，柱后的流动相应由定常逐渐失稳，慢慢变得越发复杂，最后到达超临界区的湍流分离。对于300≤Re≤3×105的亚临界区，柱面边界层为层流，而尾流却已变为湍流涡街［6］。天然河道等实际情况中，雷诺数相对较大，通过实验研究发现，亚临界区桩柱的绕流情况已基本能反映出较高雷诺数下天然河道的绕流特性。

本文运用CFD软件、基于RNGk⁃ε模型对亚临界雷诺数下单圆柱和单方柱绕流进行了数值模拟，计算得到了这两种情况下的阻力系数、Strouhal数等重要动力学参数，同时模拟出了桩柱绕流过程中的漩涡脱落、流场演变等情况，为桩柱绕流问题的实际物理机制进行了合理的仿真分析，在实际工程中具有良好的借鉴意义。

1 控制方程

不可压缩粘性流体流体的运动可用Navier⁃Stokes方程［7］来描述，连续性方程与动量方程分别为

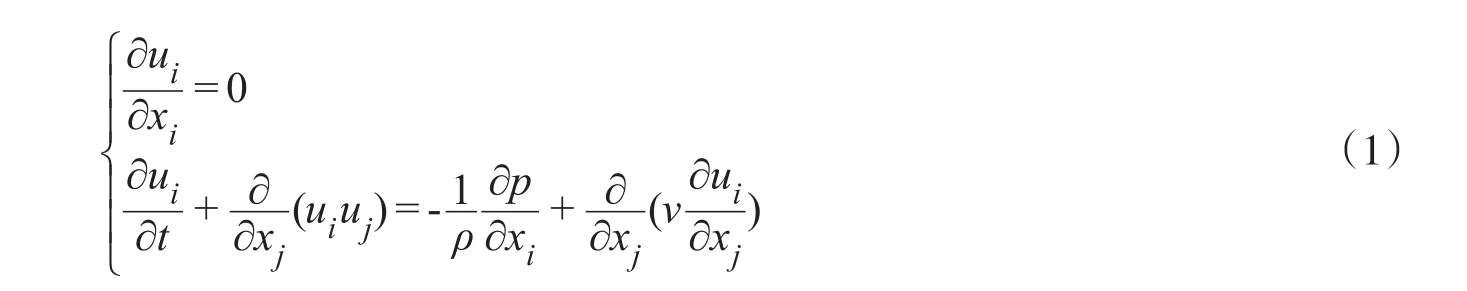
式中：ui为速度分量；p为压力；ρ为流体的密度；ν为流体的动力黏性系数。

对于湍流情况，本文采用RNGk⁃ε模型，RNGk⁃ε模型是k⁃ε模型的改进方案，由Yakhot和Orzag［8］提出，在RNGk⁃ε模型中，通过在大尺度运动和修正后的粘度项体现小尺度的影响，而使这些小尺度运动有系统地从控制方程中去除。所得到的k方程和ε方程，与标准k⁃ε模型非常相似［9］，其表达式如下

式中：Gk为由于平均速度梯度引起的湍动能k的产生项，μeff=μ+μt，μt=ρCμk2/ε；经验常数Cμ=0.084 5，αk=αε=1.39，C2ε=1.68。

相对于标准k⁃ε模型，RNG k⁃ε模型通过修正湍动粘度，考虑了平均流动中的旋转及旋转流动情况，同时在ε方程中加入了一项Rε，从而反映了主流的时均应变率Eij，这样该模型中产生项不仅与流动情况有关，而且在同一问题中也还是空间坐标的函数。从而，RNGk⁃ε模型可以更好的处理高应变率及流线弯曲程度较大的流动［10］。

2 数值算法

2.1 有限元建模

建模过程中，运用大型通用流体力学计算软件Fluent辅助计算。计算区域采用分块结构化网格，柱体表面网格做加密处理，边界区网格相对稀疏，如图1所示，计算区域为33D×15D（D为圆柱直径和方柱边长），模型上游来流区域为7D，下游尾流区域为25D，上下边界取7D。流体自左向右流动。

图1 单圆柱、单方柱计算区域及柱面网格Fig.1 Computational domain and surface grid of a circular cylinder and a square cylinder

2.2 边界条件

入流边界条件：u=V，v=0。

出流边界条件：自由出流。

壁面条件：上下边界及柱体表面为无滑移固壁边界。

2.3 计算模型参数

计算模型采用RNGk⁃ε模型，压力速度耦合方式为PISO算法，动量、湍动能和湍动耗散率均采用二阶迎风格式。其中，雷诺数、来流速度等参数见表1所示。

表1 计算模型参数Tab.1 Computational model parameters

2.4 模型验证

由边界层理论可知，液体对所绕流物体的阻力包括固体表面摩擦阻力和由压强分布不均造成的压强阻力。同样被绕流物体阻力系数Cd也来源于壁面粘性摩擦与表面压力系数，Strouhal数是一个反应漩涡脱落的频率相对于来流速度快慢的重要无量纲参数，二者定义为

式中：Fd为绕流阻力，D为圆柱直径或方柱边长；u为来流速度；f为涡街脱落频率；ρ为流体密度。

为验证本文中数值模拟的正确性，计算得到了亚临界雷诺数下单圆柱及单方柱在不同雷诺数下的绕流阻力系数Cd及Strouhal值，并将其与文献中的计算结果相对比，结果如表2、表3所示。其中，Cd代表柱体阻力系数平均值。

通过表2、表3中数据发现，对亚临界雷诺数下圆柱、方柱绕流模拟计算得出的结果能很好的与参考文献中数据相吻合，即验证了本文计算结果的正确性。

同时，根据表2、表3中的数据绘制亚临界雷诺数下圆柱和方柱的绕流阻力系数Cd及Strouhal值随雷诺数的变化曲线，如图2所示。

表2 单圆柱绕流模拟计算结果Tab.2 Simulation results of flow around a circular cylinder

表3 单方柱绕流模拟计算结果Tab.3 Simulation results of flow around a square cylinder

图2 阻力系数与Strouhal数随雷诺数走势Fig.2 Trends of drag coefficient and Strouhal number with the change of Reynolds numbers

从图2中可以看出亚临界雷诺数下圆柱和方柱绕流阻力系数Cd及Strouhal数值曲线都相对平稳，其值变化不大，圆柱和方柱的Strouhal数分别在0.2和0.13上下微小波动。同一雷诺数下圆柱绕流阻力系数较方柱要小，但圆柱的Strouhal数却略大于方柱，说明圆柱绕流阻力弱于方柱，漩涡脱落频率相对于来流速度却更快。

3 结果分析

由于文章篇幅有限，结果数据较多。在此，结合大量文献资料及实际计算数据，只选择当雷诺数Re=22 000时的典型情况进行着重分析讨论。

3.1 绕流阻力系数及升力系数

当雷诺数Re=22 000时，压强阻力显著大于摩擦阻力，占主导地位，此时的阻力系数主要来源于柱体表面的压力系数。绕流升力是由垂直于来流方向柱体两侧压力不均造成。由图3可以看出，圆柱、方柱绕流阻力系数Cd、升力系数Cl都呈周期性单一频率振动，但方柱的Cd、Cl迭代周期明显大于圆柱。方柱升力系数Cl幅值较圆柱更大，说明脉动较强。

3.2 流场演变

如图4、图5所示，为单圆柱与单方柱在雷诺数Re=22 000时一个漩涡脱落周期内5个典型时刻的流线图及涡量图。

图3 单圆柱与单方柱绕流阻力、升力系数Fig.3 Lift and drag coefficients of a circular cylinder and a square cylinder

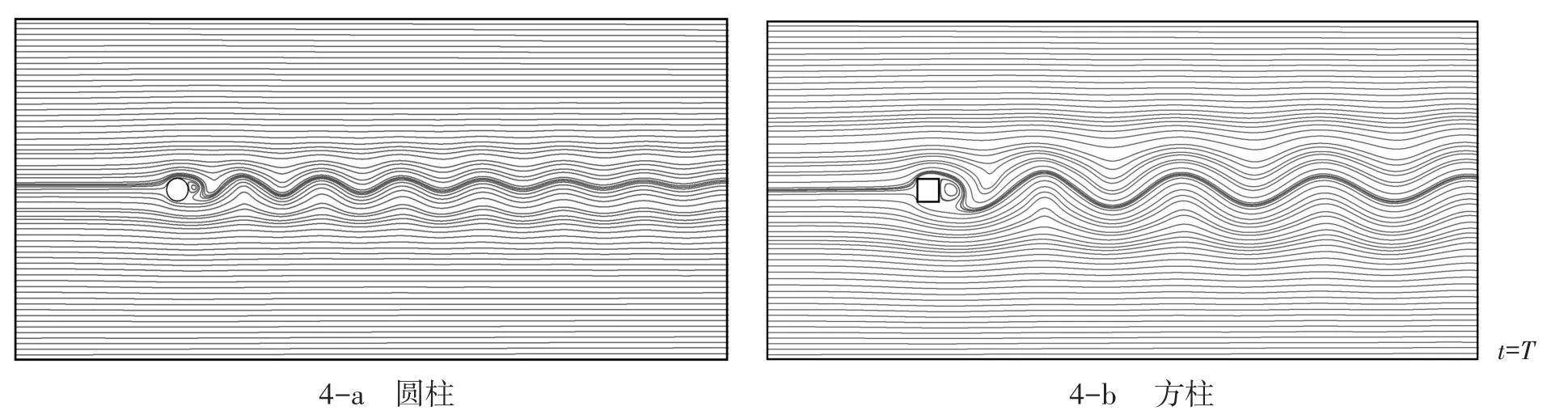
图4 单圆柱与单方柱绕流漩涡脱落周期内不同时刻流线图Fig.4 Streamlines of the flow around a circular cylinder and a square cylinder at different time in a vortex shedding cycle

图5 单圆柱与单方柱绕流漩涡脱落周期内不同时刻涡量等值线图Fig.5 Vorticity contours of the flow around a circular cylinder and a square cylinder at different time in a vortex shedding cycle

图4、图5为一个周期内5个典型时刻的流线图和涡量图，由图可以看出0和T时刻的流线图、涡量图基本相同，且二者对称于T/2时刻图像，T/4时刻图像同样对称于3T/4时刻图像。此5个典型时刻图像生动的表明出了单圆柱、单方柱绕流流场运动及漩涡脱落呈周期性变化的特性。在0时刻，柱后偏上位置产生一个大漩涡，致使柱的绕流升力达到最大，新生的漩涡随着水流向下方迁移，至T/4时刻，到达柱的正后方，此时升力为零。由于液体的粘滞性，从柱上方迁移下来的漩涡在运动过程中能量逐渐衰减，最后消失，漩涡完成脱落。T/2时刻柱后偏下位置产生漩涡，此时升力同样最大，漩涡的脱落等同于柱后上方漩涡的脱落特性。一个周期完成，下个周期开始，由此在柱后形成两列交错且周期性摆动的漩涡，即Karman涡街，圆柱、方柱都是如此，说明二者绕流流场运动及漩涡脱落具有相似特性，只是两者柱体表面旋涡脱落周期大小不同，圆柱较方柱偏小，即同一雷诺数下圆柱绕流旋涡脱落频率大于方柱绕流旋涡脱落频率。

3.3 边界层分离

亚临界雷诺数下圆柱、方柱绕流边界层分离同为层流分离，且边界层内液体运动伴有能量损失，但通过模拟发现二者分离点有很大区别，对于圆柱，随着雷诺数的增大分离点逐渐向后推移。液流与柱面分离原理（图6）：在压强最大的P点至柱上下A、B两点的边界层内液流处于加速减压状态，压能除部分转化为动能外主要补偿能量损失，在A、B两点时压强最小，流速最大，两点之后液流处于减速增压状态，当动能减小至零而无法提供给压能时，完成分离。

而对于方柱，由于柱体有凸出的棱角，绕流情况就变的不如圆柱绕流那样复杂，分离点固定在方柱的前两个棱角位置，如图6中C、D两点。

图6 圆柱和方柱绕流示意图Fig.6 Sketch of flow around circular and square cylinder

4 结论

运用CFD软件，通过对亚临界雷诺数下的单圆柱和单方柱绕流进行数值模拟与对比，本文得出以下结论：

（1）柱体绕流模拟中，网格的精度与划分方式对计算结果有很大影响，为了得到更精确的结果同时又节省计算时间，要选取数量适当的网格及合适的网格划分方式进行计算，同时对柱体表面及柱后方轴线区域网格做加密处理。

（2）亚临界雷诺数下，圆柱和方柱绕流阻力系数都变化不大，Strouhal数更是趋向于定值，阻力系数及升力系数都呈周期性单一频率振动。同一雷诺数下圆柱绕流阻力系数较方柱绕流阻力系数要小，但圆柱的Strouhal数较方柱的要高。

（3）同一雷诺数下，单圆柱和单方柱绕流生成的旋涡脱落周期不同，方柱的偏大，但二者漩涡脱落特征与流场运动具有相似特性。

（4）亚临界雷诺数下，圆柱和方柱绕流边界层分离点不同，圆柱的分离点随着雷诺数的增大而逐渐向柱后方推移，方柱的分离点则固定在柱前两个棱角位置。

［1］Slaoutiand A,Stansby P K.Flow around two circular cylinders by the random⁃vortex method［J］.Journal of Fluids and Structures,1992,6：641-670.

［2］苏铭德,康钦军.亚临界雷诺数下圆柱绕流的大涡模拟［J］.力学学报,1999,31（1）：100-105.

SU M D,KANG Q J.Large eddy simulation of the turbulent flow around acircular cylinder at subcritical Reynolds numbers［J］.Acta Mechanica Sinica,1999,31（1）：100-105.

［3］Kawai,Hiromasa,Fujinamic,et al.Numerical simulation of flow around square prisms in tandem arrangements［C］//Gulf.9th IC⁃ME.Houston Tx：Gulf Publishing,1995：185-186.

［4］王远成,吴文权.方柱绕流流场的RNG方法模拟研究［J］.水动力学研究与进展,2004（19）：916-920.

WANG Y C,WU W Q.Numerical simulation of flow around square cylinder using RNGk⁃εturbulence model［J］.Journal Hydro⁃dynamics,2004（19）：916-920.

［5］顾志福,孙天风,林荣生.高雷诺数时串列双圆柱平均压力的实验研究［J］.空气动力学学报,1997,15（3）：393-399.

GU Z F,SUN T F,LIN R S.Experimental research of average pressure of two circular cylinder in tandem arrangement at high Reynolds number［J］.Acta Aerodynamica Sinica,1992,15（3）：393-399.

［6］杨烁,吴宝山.二维圆柱绕流数值模拟［J］.中国造船,2007（48）：533-540.

YANG S,WU B S.The numerical simulation of two dimensional circular flow［J］.China Shipbuilding,2007（48）：534-540.

［7］张远君.流体力学大全［M］.北京：北京航空航天大学出版社,1991.

［8］Yakhot V,Orzag S A.Renormalization grop analysis of turbulence［J］.Basic theory.J Scient Comput,1986,1：3-11.

［9］Versteeg H K,Malalasekera W.An Introduction to Computational Fluid Dynamics［M］.Wiley：The Finite Volume Method,1995.

［10］王福军.计算流体动力学分析［M］.北京：清华大学出版社,2004.

［11］史里希廷H.边界层理论［M］.北京：科学出版社,1988.

［12］Lyn D A,Einav S,Rodi W.A Laser Doppler Velocimetry Study of Ensemble⁃averaged Chsrscteristic of the Turbulent Flow Near of a Square Cylinder［J］.Fluid Mechanics,1995,304：285-319.

［13］Lyn D A,Rodi W.The flapping shear layer formed by flow separation from the forward corner of a square cylinder［J］.Fluid Mesh,1994,267：353-376.

Numerical simulation of the flow around circular and square cylinder at sub⁃critical Reynolds numbers

SHEN Li⁃long，LIU Ming⁃wei，WU Lin⁃jian，LI Peng⁃fei，SHU Dan
（National Inland Waterway Regulation Engineering Research Center,Key Laboratory of Hydraulic&Waterway Engineering of the Ministry of Education,Chongqing Jiaotong University,Chongqing400074,China；School of River&Ocean Engineering，Chongqing Jiaotong University，Chongqing400074,China）

With theRNG k⁃εmodel and the finite volume method，the flow around a two⁃dimensional circular cylinder and a two⁃dimensional square cylinder at sub⁃critical Reynolds numbers was simulated and evaluated,and the trends of drag coefficients and Strouhal numbers with the change of Reynolds numbers from 3×102to 3×105were obtained.Meanwhile,characteristics of the flow around a circular cylinder and a square cylinder atRe=22 000 have been compared and analyzed in detail.Calculation results show that drag coefficient of flow around a circular cylinder is lower than the drag coefficient of flow around a square cylinder with the same Reynold number.Howev⁃er,the Strouhal number of flow around a circular cylinder is slightly higher than the Strouhal number of flow around a square cylinder.Though their boundary layer separation points are different,the flow field evolution and the vor⁃tex shedding of two cylinders have some similarities.

sub⁃critical Reynolds numbers；circular and square cylinder；flow around body；numerical simula⁃tion；RNG k⁃εmodel

TV 143+.2；O 351

A

1005-8443（2014）03-0227-07

2013-11-28；

2014-01-06

国家科技支撑计划项目（2012BAB05B04）

沈立龙（1990-），男，山东省菏泽市人，硕士研究生，主要从事港口海岸工程结构与基础方面的研究。