天津滨海软黏土蠕变特性及其经验模型研究

王元战，董焱赫

（天津大学 建筑工程学院，天津市港口与海洋工程重点实验室，天津 300072）

天津滨海软黏土蠕变特性及其经验模型研究

王元战，董焱赫

（天津大学 建筑工程学院，天津市港口与海洋工程重点实验室，天津 300072）

在室内三轴蠕变试验的基础上，分析了天津滨海地区重塑饱和软黏土的非线性蠕变特性。蠕变试验采用分级加载的方式进行，利用“陈氏法”对实测数据进行处理，得到饱和软黏土在不同应力状态下的蠕变试验曲线。在此基础上，依据黏土的应力-应变、应变-时间关系，分别用Singh⁃Mitchell和Mesri经验模型拟合试验数据。总结拟合结果，结合滨海软黏土的蠕变特性，提出一种分段拟合的Mesri模型，在蠕变前期，模型的应力-应变关系采用双曲线函数，应变-时间关系采用幂函数；在蠕变后期，模型的应力-应变关系采用双曲线函数，应变-时间关系采用双曲线函数，以两条拟合曲线的交点作为分段拟合的分界点。对比分析表明，该方法能更好地描述具有衰减稳定特性的蠕变曲线。选取天津滨海地区原状土蠕变试验数据对该模型进行验证，拟合结果较好，由此建立了适用于具有衰减稳定蠕变特性的滨海软黏土非线性蠕变模型。

软黏土；蠕变；衰减稳定；经验模型；天津滨海

Biography：WANG Yuan⁃zhan（1958-），male，professor.

在中国经济发展活跃的长江口、珠江口、天津滨海等海岸地区，广泛分布着软黏土地基，这些地区经济发展迅速，在这些软土地基上兴建了大量的建筑物，以天津港为例，港口规模不断扩大，吞吐量已经跃居世界第四，大量的陆域设施和围海造陆工程正在建设中。但由于该种土类流变效应较为明显，静载条件下变形缓慢增加，即发生蠕变效应，使得这些建在工程病害层上的建筑物存在着不同程度的沉降，使之有失稳、滑塌的危险。如近年天津北疆高桩码头多个转角处由于软黏土岸坡土体的蠕变发生了基桩连同桩帽与上部结构之间出现较大相对变位的现象，导致横梁的搁置长度不足，有的只剩下了几厘米，使得码头结构处于危险状态之中［1］。开展滨海软黏土的蠕变试验研究，建立其合适的蠕变模型，是亟待开展的工作，对研究滨海地区港口码头和防波堤结构的长期稳定性有着重要意义。关于长期荷载下软黏土的蠕变特性的问题，学者们展开了大量的研究。

在国外，Zhen［2］等在Perzyna超限应力理论的基础上，建立了一个各向异性的黏弹塑性软黏土模型，并针对法国St.Herblain地区的软土进行了等应变率蠕变试验，对所建立的模型进行了验证；Leoni［3-5］等和Ver⁃meer等考虑土体各向异性，建立软土蠕变模型，并对软土的蠕变行为进行数值模拟研究。Kelln［6］等尝试采用粘弹力学原理揭示软粘土的蠕变行为。在国内，李军世［7］等采用Singh⁃Mitchell应变速率-时间关系方程描述土体的蠕变特性，结合上海淤泥质黏土室内试验，给出了上海淤泥质黏土的蠕变形式；王常明［8］等的三轴蠕变试验研究表明，滨海相沉积的软土具有非线性蠕变的特性，双曲线模型更适合其应力-应变关系，修改了Singh⁃Mitchell模型的应力-应变关系，建议了滨海软土应力-应变-时间关系模型。王元战［9］等基于屈服理论，研究了天津滨海淤泥质软黏土的蠕变变形规律，建立了反映滨海软黏土的非线性流变本构模型；闫澍旺［10］等，采用大直径原状试样进行了三轴不固结不排水蠕变试验，研究了天津滨海新区吹填黏土的蠕变变形的规律性，在此基础上建立天津滨海新区软黏土的无屈服面蠕变模型；王元战［11］等采用Merchant蠕变模型三轴蠕变试验的结果曲线进行拟合，建立了适用于天津滨海地区的软黏土本构模型。

虽然目前有很多关于土体蠕变模型的研究成果，也不乏对天津滨海软黏土蠕变特性的研究，但是这些成果不足以完全诠释天津滨海地区软黏土的蠕变特性，原因有2个：一是蠕变模型自身复杂性和局限性。二是以往研究得出的模型大多只能描述自身的试验数据，没有用其他试验数据加以验证，缺乏综合比较与分析。

本文以天津港病害层重塑淤泥质黏土为例进行蠕变试验研究。依据试验数据，结合Singh⁃Mitchell和Mesri经验蠕变模型，提出一种分段拟合的Mesri模型，在蠕变前期，模型的应力-应变关系采用双曲线函数，应变-时间关系采用幂函数；在蠕变后期，模型的应力-应变关系采用双曲线函数，应变-时间关系采用双曲线函数，以两条拟合曲线的交点作为分段拟合的分界点。对比分析表明，该模型能更好地描述具有衰减稳定特性的蠕变曲线。选取以往天津滨海地区两种典型软黏土蠕变试验数据对该模型进行验证，拟合结果较好，由此建立了适用于具有衰减稳定蠕变特性的滨海软黏土非线性蠕变模型。

1 三轴蠕变试验

1.1 试验设备及试样

设备采用的是无级加载应力控制式三轴蠕变试验仪，该三轴蠕变试验仪由普通应变式三轴仪通过改装轴向加载设备而成，仪器主要由轴向加载设备、围压控制测量系统、反压控制测量系统、体积变化和孔隙水压力测量系统等组成，将轴向加载设备由原来的应变控制式改造成应力控制式加载。这样改造试验仪器简单易行，且既可以利用原有应变式三轴仪器设备优良稳定的围压控制测量系统、反压控制测量系统、体积变化和孔隙水压力测量系统，又可以通过受力平衡计算，利用干砂和砝码施加各级轴向荷载，获得恒定且准确的轴向偏应力。

黏土试样为天津港地区5～10 m土层饱和重塑软黏土，土样呈流塑状态。依据土工试验规程（SL237-1999）制作重塑试样。试样直径39.1 mm，高为80 mm。土样的基本指标如表1所示。

1.2 试验方法及加载方案

在土的室内流变试验中，对于蠕变试验有两种不同的加载方式，即分别加载法和分级加载法。所谓分级加载，就是在同一试样上逐级加上不同的应力，即在一级应力水平下蠕变经历给定的时间或达到稳定后，将应力水平提高到下一级的水平，直到所需的应力水平［12］。为了克服分别加载的局限，减小采用不同土样进行试验对试验结果带来的离散性，本试验加载方式采用分级加载法。

由于软黏土具有渗透性差的特点，试验采用不排水蠕变试验，围压分别取50 kPa，100 kPa，150 kPa。在蠕变试验进行前，应选取同一批次重塑土样进行围压50 kPa、100 kPa和150 kPa下的固结不排水剪切试验，以试样应变达到15%为破坏标准，确定破坏偏应力qf分别为70.2 kPa，120.5 kPa和178.8 kPa。根据qf确定每级加载偏应力，取加载级数为5级，加载方案如表2所示，再通过受力平衡计算各级加砂质量。

表1 土样基本特征表Tab.1 Basic physical parameters of soil samples

蠕变试验步骤为：第1步，将制好的试样放入真空室中，将室内抽气呈负压状态，10 h以后打开排水阀，使土样进水饱和。第2步，饱和完成后，将试样安放在三轴压力室进行固结，由于软黏土排水性差，故固结时间设为24 h。第3步，固结基本完成以后，设置量测竖向变形的百分表初始读数，关闭排水阀，再施加第一级偏应力ΔF1，同时通过百分表量测轴向变形。在偏应力作用下蠕变稳定或经历给定的时间（本次试验每级偏应力施加时间确定为48 h）后，再增加配重，使偏压力达到ΔF2的水平，以此直到五级荷载施加完毕。

表2 土样分级加载方案Tab.2 Schemes of step loading kPa

1.3 试验结果分析

限于篇幅，以下以围压100 kPa下的蠕变试验为例，进行分析。试验得到的曲线为分级加载下的应变-时间曲线，该流变曲线的可用性较小，需要分级进行整理，通常的整理方法有线性法和陈氏法。线性法是将土体视为线性流变体，此时土体蠕变响应满足线性叠加原理，蠕变曲线可以简单地由每一级荷载的蠕变响应叠加而成。

若要更准确的研究土的蠕变，应将土体视为非线性流变体。由陈宗基教授提出并由他的学生所发展的“陈氏法”通过采用适当的实验技术与方法，用作图法建立真实变形过程的叠加关系，在考虑土体为非线性流变体或线性流变体时均可适用，在国内外岩土流变学研究中得到越来越广泛的应用。陈氏法可以使蠕变试验通过采用适当的加载程序从单一试样得到更多的试验资料，这对试验周期长，并且试验价格昂贵的岩土蠕变性质研究有重大的实际意义。本试验对蠕变试验结果采用的整理方法就是陈氏法。

用“陈氏法”处理得到不同应力状态下的轴向应变与加载时间的蠕变关系曲线如图1所示，由图1可知：（1）在不排水条件下，当主应力差达到破坏偏应力前，变形呈现出明显的衰减稳态蠕变过程。在各级应力下，应变随着时间的增长逐渐趋于稳定。当主应力差较低时，应变呈现出明显的衰减蠕变趋势，蠕变现象不明显；当应力水平较高时，试样蠕变曲线包括衰减阶段和稳态蠕变阶段，试样稳态蠕变阶段的斜率随主应力差的增加而增加；（2）在不排水条件下，试样的应变随着偏应力水平的提高而越来越大，且增加幅度越来越大。在试样破坏之前，变形曲线并未出现加速蠕变阶段。由蠕变曲线得到的应力-应变等时曲线如图2所示：不同时刻，除初始时刻外，各个时刻的应力-应变曲线为彼此相似的曲线，可以用同一类函数描述；在同一时刻下，应力-应变曲线具有明显屈服特性，曲线呈非线性，这说明，需要用非线性的蠕变模型来描述滨海软黏土蠕变特性。

图1 应变-时间关系图Fig.1 ε⁃t curves of creep test

图2 应力-应变等时曲线Fig.2 σ⁃ε isochronal curves

2 蠕变经验模型

蠕变的经验模型，是从流动理论或老化理论出发，直接给出土蠕变方程的应力-应变-时间函数形式。对每种不同的材料，甚至不同的条件，有多样的经验模式，和元件模型、屈服面模型、内时模型等相比，它比较直观，参数简单且容易获取，亦为工程设计人员所乐意采用。目前常用的具有代表性的包括Singh⁃Mitchell蠕变速率和蠕变函数，常速率轴向应变条件下的双曲线计算模型以及Mesri应力-应变-时间蠕变函数等。

2.1 Singh⁃Mitchell模型

1968年Singh等提出的著名的Singh⁃Mitchell经验蠕变模型［13-14］是在总结了单级常应力加载，排水与不排水三轴压缩试验数据的基础上，采用指数函数表示应力-应变关系、采用幂函数表示应变-时间关系的经典的经验蠕变模型，该模型能够很好地反映土的蠕变特性。Singh⁃Mitchell蠕变模型写成应变率-应力水平-时间的关系式，可表示为

式中：ε˙为任一时刻t的轴向应变速率；t为试样受荷时间；Dr=（σ1-σ3）/（σ1-σ3）f为偏应力水平，（σ1-σ3）f为破坏偏应力，可由常规三轴排水压缩实验得到；Ar是在单位参考时刻tr，偏应力水平为零时的应变速率；m由ln˙-lnt拟合直线的斜率确定；α为应变速率对数与剪应力关系图中线性段的斜率。

对式（1）进行积分，在不考虑初始应变且m不为1时。经推导可得

式中：B=Artr/（1-m）；β=α；λ=1-m。该模型需要确定的3个参数是B，β，λ。

2.2 Mesri模型

针对Singh⁃Mitchell模型存在的局限性，Mesri.G［15-16］于1981年提出了新的经验模型。该模型应力-应变关系采用双曲线函数，应变-时间关系仍采用幂函数。经典的Mesri模型公式如下

式中有3个参数：参考应变2/（Eu/Su），拟合比Rf和蠕变参数λ。

用Singh⁃Mitchell模型和Mesri模型分别拟合试验曲线，拟合结果如图3和图4所示。

2.3 分段拟合的Mesri模型

从拟合结果可以看出，Mesri模型和Singh⁃Mitchell模型都存在后期拟合不准确的情况，原因在于两个模型的应变-时间关系都采用了幂函数的形式，而幂函数是非衰减函数，当时间增大时，曲线斜率较大，对应的应变值远大于实测值，对于尚处于衰减稳定期的试验数据是不适用的。

2.3.1变形函数（应力-应变关系）的确定

当取某一时刻t1时，公式（2）和（3）分别转化为t1时刻的应力-应变方程。以100 kPa围压下的实测数据为例，取t1=1 d，分别用两种函数去拟合试验数据，通过应变对数-偏应力水平曲线（图5）可以看出，当偏应力水平处于中间段时，实测数据呈线性关系，而在偏应力水平趋近于1或趋近于0时，实测数据则呈现出明显的非线性；指数函数关系只能描述偏应力水平处于中间段（20%～80%偏应力水平）的应力-应变关系，而双曲函数能够准确地描述全部应力水平下的状态。故应力-应变关系应采用双曲线函数描述。

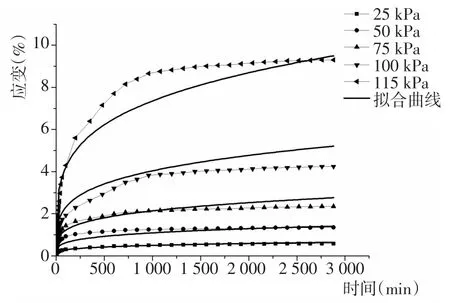
图3 试验与Sing⁃Mitchell模型计算结果比较Fig.3 Comparison between test data and calculated results using S⁃M model

图4 试验数据与Mesri模型计算结果比较Fig.4 Comparison between test data and calculated results using Mesri model

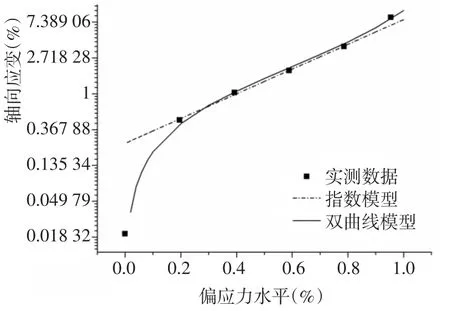
图5 应力-应变等时曲线Fig.5 σ⁃ε isochronal curves

2.3.2 蠕变函数的确定

结合上文研究，为了修正Mesri模型的误差，由C.C.维亚洛夫提出的通用的时间函数［17］入手，本文建议了一种分段拟合的经验模型，该模型前期仍采用Mesri函数的形式；在拟合后期数据时将Mesri函数应变-时间关系修正为双曲线函数，该函数的形式为

式中：T为蠕变参数，2/（Eu/Su）和Rf为t=∞时应力-应变方程的参考应变和拟合比，故该修正模型共有3个参数需要确定。

2.3.3 Mesri模型参数的确定

令t1=1 440 min（1 d），此时的应力-应变函数表示t=1 d时的应力-应变关系，即

以ε/Dr为纵坐标，ε为横坐标，将公式（5）转换为线性方程的形式，对试验数据进行线性拟合。直线的截距即为t1=1 440 min（1 d）时刻下的参考应变2/（Eu/Su），斜率即为拟合比Rf。拟合结果如图6所示。

应变-时间双对数曲线如图7所示。图7中，各个偏应力下的曲线呈线性分布，对各个曲线进行线性拟合，各条直线斜率的平均值即为λ。

2.3.4 修正的Mesri模型参数的确定

由公式（4），当t=∞时，公式变为

将公式（6）代入公式（4）得

设Y=t/ε，a=1/ε∞，b=T/ε∞，将式（7）变换为Y=ax+b的线性形式，所得t/ε–t关系如图8所示。将图中数据进行线性拟合，分别得到5级荷载下T的值，并可以求出各级偏应力下的ε∞。

以ε∞/Dr为纵坐标，ε∞为横坐标，将公式（6）转换为线性方程的形式，对t=∞时刻的应力-应变关系进行线性拟合。直线的截距即为t=∞时刻下的参考应变2/（Eu/Su），斜率即为拟合比Rf。拟合结果如图9所示。

2.3.5 分段拟合的蠕变模型

通过以上步骤分别得到Mesri模型和修正Mesri模型的拟合曲线，由于Mesri模型能够较好地描述蠕变的衰减阶段，而修正的Mesri模型能够较好地描述低蠕变速率的稳态蠕变阶段。分别用两函数拟合试验数据，用修正的Mesri函数修正经典Mesri函数的拟合曲线。经过分析，以两条曲线的交点作为分段拟合的分界点，交点对应时刻为tj，当0＜t＜tj时，黏土的蠕变特性用Mesri模型描述，当t≥tj时，黏土的蠕变特性用修正的Mesri模型描述。最终的拟合参数如表3所示。用分段拟合的Mesri模型对试验曲线进行拟合，所得结果如图10～图12所示。比较图11与图3和图4，分段拟合的Mesri模型能够更好地描述试验数据的蠕变特性，尤其是对蠕变后期的预测要优于经典的Mesri模型和Singh⁃Mitchell模型。

图6 ε/Dr⁃ε关系曲线Fig.6 ε/Drwith ε under confining pressure of 100 kPa

图7 lnε-lnt关系曲线Fig.7 Relationships between lnε and lnt

图8 100 kPa围压下蠕变试验数据换算曲线Fig.8 Conversion of creep curves under 100 kPa confining pressure

图9 ε∞/Drε∞关系曲线Fig.9 ε∞/Drwith ε∞ under confining pressure of 100 kPa

3 模型在滨海原状土试验数据的验证

天津滨海地区的淤泥质、粉质黏土层多呈灰色，有机质含量丰富，具有高含水率、高孔隙比、低强度、高压缩性、低渗透性等特点。

为了验证分段拟合的Mesri模型，选取天津港北疆码头淤泥质黏土及粉质黏土的原状土蠕变试验数据，试验数据来自文献［14］，试样是现场钻孔取得的原状土，土性参数如表4。

表3 分段拟合的各个参数值Tab.3 Values of parameters for piecewise fitting

依据土层深度，分别选取100 kPa围压下淤泥质黏土和200 kPa围压下粉质黏土的蠕变试验数据。加载等级分为4级，对于淤泥质黏土，各级偏压分别为25 kPa、50 kPa、75 kPa和100 kPa，固结不排水（CU）试验的破坏偏压力为134.4 kPa；对于粉质黏土，各级偏压力分别为50 kPa、100 kPa、150 kPa和200 kPa，破坏偏压力为244.9 kPa。

用分段拟合的Mesri模型去拟合试验曲线，拟合结果如图13、图14所示。各项参数见表5。

由图13、图14，比较拟合曲线与实测曲线，发现对于淤泥质黏土，分段拟合的Mesri模型能够准确地描述其蠕变特性，拟合精度较高；对于粉质黏土，除较高应力状态下拟合结果存在一定误差外，其余拟合曲线基本与实测曲线一致，且最大误差能够控制在10%以内。蠕变函数能够很好的描述天津滨海淤泥质黏土和粉质黏土的蠕变特性。

表4 土样基本特征表Tab.4 Basic physical parameters of soil samples

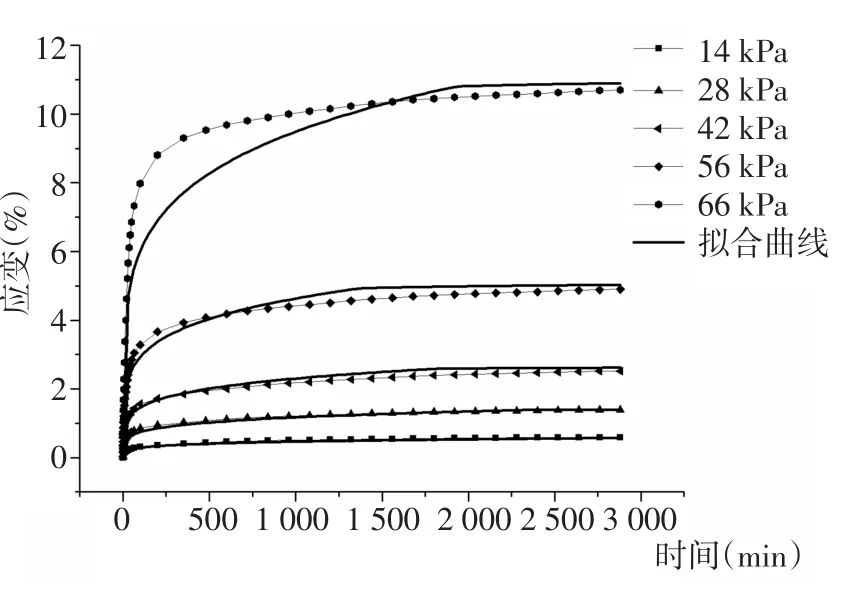
图10 围压50 kPa下蠕变拟合曲线Fig.10 Fitting creep curves under 50 kPa confining pressure

表5 分段拟合模型的各个参数值Tab.5 Values of parameters for modified Mesri model

图11 围压100 kPa下蠕变拟合曲线Fig.11 Fitting creep curves under 100 kPa confining pressure

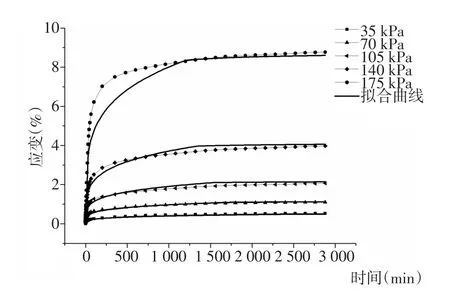
图12 围压150 kPa下蠕变拟合曲线Fig.12 Fitting creep curves under 150 kPa confining pressure

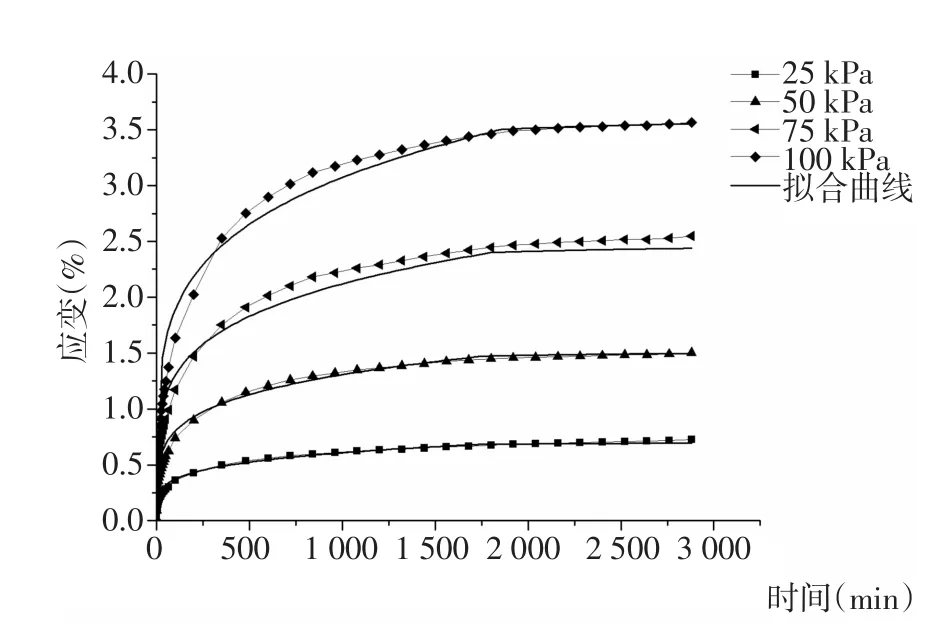
图13 围压100 kPa下淤泥粘土蠕变拟合曲线Fig.13 Fitting creep curves of muddy clay under 100 kPa confining pressure

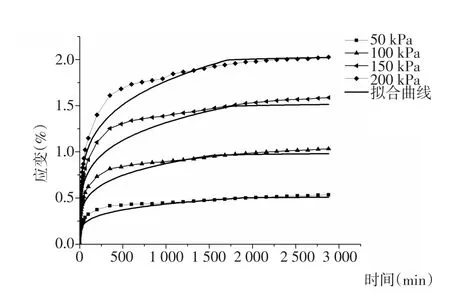
图14 围压200 kPa下粉质粘土蠕变拟合曲线Fig.14 Fitting creep curves of silt clay under 200 kPa confining pressure

4 结论

通过室内三轴蠕变试验，得到了天津港地区重塑饱和软黏土在不同围压状态下的应变-时间关系及应力-应变等时关系，建立了分段拟合的Mesri经验蠕变模型，通过对试验结果和模型的分析得到以下结论。

（1）在不同围压，以及各级偏应力作用下，蠕变试验曲线具有明显的衰减稳定特性，没有加速蠕变阶段；应力-应变等时曲线具有明显的非线性特征，除初始时刻外，其余曲线为彼此相似曲线，可以用同一类非线性应力-应变函数描述。

（2）在总结试验结果和现有经验蠕变模型的基础上，建立了修正的Mesri模型，该模型将应变-时间关系修正为双曲线关系，用于对Mesri模型的拟合曲线加以修正。在此基础上，建议了一种分段拟合的Mesri模型，用Mesri模型描述蠕变的衰减阶段，用修正的Mesri模型描述蠕变的稳态阶段，以两条拟合曲线的交点作为分段拟合的分界点。该模型更符合文中试验数据，能够更好地反映和预测具有衰减稳定特征的滨海软黏土的蠕变特性。

（3）选取天津滨海地区典型淤泥质黏土和粉质黏土的原状土蠕变试验数据对分段拟合的Mesri模型进行验证，拟合结果较好，由此建立了适用于具有衰减稳定蠕变特性的滨海软黏土非线性蠕变模型。

［1］李越松,赵冲久,赵利平,等.天津港岸坡土体蠕变对高桩码头的影响［J］.中国港湾建设,2009（4）：5-8.

LI Y S,ZHAO C J,ZHAO L P,et al.Influence of bank soil creep deformation on high-piled wharf in Tianjin port［J］.China Har⁃bor Engineering,2009（4）：5–8.

［2］YIN Zhen⁃Yu,CHANG Ching S,MINNA Karstunen,et al.An anisotropic elastic⁃viscoplastic model for soft clays［J］.Interna⁃tional Journal of Solids and Structures,ASCE,2010,47（5）：665-677.

［3］LEONI M,VERMEER P A,KARSTUNEN M.Validation of Anisotropic Creep Model for Soft Soils［C］//KARSTUNEN M,LEO⁃NI M.Geotechnics of Soft Soils：Focus on Ground Improvement.Glasgow：Taylor&Francis,2008：165-171.

［4］LEONI M,KARSTUNEN M,VERMEER P A.Anisotropic creep model for soft soils［J］.Geotechnique,2008,58（3）：215-226.

［5］VERMEER P A,LEONI M,et al.Modeling and Numerical Simulation of Creep in Soft Soils［C］//CHAN D H,LAW K T.Soft Soil Engineering.Vancouver：Taylor&Francis,2007：57-71.

［6］ KELLN C,SHARMA J,HUGHES D,et al.An Improved Elastic⁃viscoplastic Soil Model［J］.Canadian Geotechnical Journal,2008,45（10）：1 356-1 376.

［7］ 李军世,孙钧.上海淤泥质黏土的Mesri蠕变模型［J］.土木工程学报,2001,34（6）：74-79.

LI J S,SUN J.Mesri′s creep model for Shanghai silt⁃clay［J］.China Civil Engineering Journal,2001,34（6）：74-79.

［8］王常明,王清,张淑华.滨海软土蠕变特性及蠕变模型［J］.岩石力学与工程学报,2004,23（2）：227-230.

WANG C M,WANG Q,ZHANG S H.Creep characteristics and creep model of marine soft soils［J］.Chinese Journal of Rock Me⁃chanics and Engineering,2004,23（2）：227－230.

［9］王元战，王婷婷，王军.滨海软土非线性蠕变模型及其工程应用研究［J］.岩土力学,2009,30（9）：2 679-2 685.

WANG Y Z,WANG T T,WANG J.A nonlinear rheological model of soft clay and its application to Tianjin littoral area［J］.Rock and Soil Mechanics,2009,30（9）：2 679-2 685.

［10］闫澍旺,刘克瑾,李伟,等.天津滨海新区软黏土的蠕变特性及无屈服面模型探究［J］.岩土力学,2010,31（5）：1 431-1 436.

YAN S W,LIU K J,LI W,et al.Study of creep properties of soft clay in Tianjin Binhai New Area and no⁃yield⁃surface constitu⁃tive model［J］.Rock and Soil Mechanics,2010,31（5）：1 431-1 436.

［11］王元战,黄东旭,肖忠,等.天津滨海两种典型软黏土蠕变特性试验研究［J］.岩土工程学报,2012,34（2）：379-384.

WANG Y Z,HUANG D X,XIAO Z.Experimental research on creep properties of two typical soft clays in coastal region of Tian⁃jin［J］.Chinese Journal of Geotechnical Engineering,2012,34（2）：379-384.

［12］孙钧.岩土材料流变及其工程应用［M］.北京：中国建筑工业出版社,1999.

［13］SINGH A,MITCHELL J K.General stress⁃strain⁃time function for clay［J］.Journal of the clay mechanics and foundation divi⁃sion,ASCE,1968，94（SM1）：21-46.

［14］田双珠，李越松，及春宁.天津港典型软黏土蠕变试验研究［J］.水道港口，2009,30（6）：440-443.

TIAN S Z，LI Y S，JI C N.Creep test of soft clay for Tianjin Port［J］.Journal of Waterway and Harbor,2009,30（6）：440-443.

［15］MESRI G，FEBRES⁃CORDERO E,SHIELDS D R,et al.Shear stress⁃strain⁃time behavior of clays［J］.Geotechnique,1981,31（4）：537-552.

［16］王琛,刘浩吾,许强.三峡泄滩滑坡滑动带土的改Mesri蠕变模型［J］.西南交通大学学报,2004,39（1）：15-19.

WANG C,LIU H W,XU Q.Modified Mesri′s creep model for soils in sliding zone of Xietan landslide in Three Gorges［J］.Jour⁃nal of Southwest Jiaotong University,2004,39（1）：15-19.

［17］C C维亚诺夫.土力学的流变学原理［M］.北京：科学出版社，1987：152-156.

Experimental research on creep properties of soft clays in coastal region of Tianjin and its empirical creep model

WANG Yuan⁃zhan,DONG Yan⁃he
（School of Civil Engineering,Tianjin Key Laboratory of Port and Ocean Engineering,Tianjin University,Tianjin300072,China）

Based on the indoor triaxial creep tests,the nonlinear creep properties of the remoulded saturated soft clay in coastal area of Tianjin were analyzed.The creep tests were carried out by the step loading method,and the creep curves of the soft clay under different stress states were got by processing the measured data by Mr.Chen′s method.In addition,Singh⁃Mitchell model and Mesri model were respectively used to fit the test curves which are the stress⁃strain isochronal curves and strain⁃time curves.Combining with the fitting results and the creep proper⁃ties of the coastal clay,a piecewise fitting Mesri model was put forward.In the early stage of the creep,the hyperbol⁃ic function was taken to describe the stress⁃strain relationship,and the power function was used to describe the strain⁃time relationship.In the late stage of the creep,two different kinds of hyperbolic functions were respectively used to matching the stress⁃strain relationship and the strain⁃time relationship.The intersection of the fitted curves was taken as the cut⁃off point.Compared with Singh⁃Mitchell and Mesri model,this model is more suitable to reflect the attenuation and stable state of the creep characteristics.The test data of two kinds of typical undisturbed clay in Tianjin which are muddy clay and silt clay were taken to verify this model.The fitting results were good.So a non⁃linear creep model which is suitable for the soft clay in the coastal area of Tianjin is established.

soft clay;creep;attenuation and stable state property;empirical creep model;coastal region of Tianjin

TV 443；O 242.1

A

1005-8443（2014）03-0209-08

2013-09-22；

2013-10-18

国家自然科学基金项目（51279128）

王元战（1958-），男，教授，博士生导师，主要从事港口海岸及近海工程结构设计理论和方法、土与结构相互作用等方面的研究。