环形钢丝绳隔振器动态特性建模与参数识别
王红霞,龚宪生,刘 巍,潘 飞
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.重庆大学机械工程学院,重庆 400044;3.湖北汽车工业学院,湖北 十堰 442002)
环形钢丝绳隔振器动态特性建模与参数识别
王红霞1,2,3,龚宪生1,2,刘 巍1,2,潘 飞1,2
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.重庆大学机械工程学院,重庆 400044;3.湖北汽车工业学院,湖北 十堰 442002)
设计一种采用独立钢丝绳圈作为弹性阻尼元件的环形钢丝绳隔振器。由于其结构的独特性,该隔振器具有非线性弹性刚度和垂向非对称迟滞动态特性。针对该特性,提出一种改进的归一化Bouc-Wen模型,采用分阶段识别方法进行参数辨识研究,并对提出的模型和参数识别方法进行周期性加载试验验证。结果表明:本文所提出模型以及参数识别方法对于该隔振器垂向非对称迟滞动态特性描述是非常准确有效的,为该隔振器动态设计方法奠定了基础。
环形钢丝绳隔振器;迟滞;改进的归一化Bouc-Wen模型;识别
钢丝绳隔振器是一种典型的非线性阻尼迟滞隔振装置,具有良好的干摩擦高阻尼特性,可以承受剪切、横滚和拉压载荷。广泛应用于工业、国防设备、电气设备、航空航天、车辆及船舶等领域[1-5]。传统钢丝绳隔振器的钢丝绳装夹、大螺旋定型需要通过专用工装完成,隔振器一旦成型,其弹性阻尼特性即在一定范围内确定,损坏后不易维修,只有更换。鉴于此,本文提出采用多个彼此独立的钢丝绳圈作为隔振器的弹性阻尼元件,组成如图1所示的环形钢丝绳隔振器。该隔振器绳圈装夹更换方便,组装灵活(钢丝绳绳圈个数根据需要确定),以此改变隔振器的弹性和阻尼特性;而且维修容易,可以延长隔振器使用寿命。建立理论模型对于分析掌握其动态特性具有重要意义。前人对于螺旋型钢丝绳隔振器进行了多方面的研究,并取得了许多成果。Tinker等[6]关于钢丝绳隔振器提出了速度n次方粘滞阻尼和非线性刚度组合模型,该模型与速度相关,许多研究表明[1,7-8]钢丝绳隔振器的响应与频率无关。胡海岩[9]针对钢丝绳隔振器提出了双线性迟滞模型,该模型不能准确描述环形钢丝绳隔振器在垂向承受拉压载荷时所展示的非对称迟滞响应特性。Bouc等[10-11]提出的由非线性微分方程控制的光滑滞回模型通过设置不同的模型参数来描述不同的非线性隔振器也包括钢丝绳隔振器。但是随着激励振幅增加当环形钢丝绳隔振器在垂向承受拉压载荷呈现出非对称迟滞回线时,该模型就不能准确的描述环形钢丝绳的非对称迟滞特性。针对该情况,Ni等[12-13]提出了改进的Bouc-Wen模型来描述钢丝绳隔振器的硬化重叠特性和非对称迟滞响应特性,但是采用该模型进行参数识别时,在计算时遇到了困扰。模型参数识别往往会采用迭代算法,以寻找参数最优值,合适选取初始参数非常困难,如果选取不合适就有可能无法收敛,无法识别参数或者得不到最优参数。Ikhouane等[14]介绍了一种极限环识别方法,不采用迭代算法,不存在收敛性问题。只要符合该方法的适用范围,就能准确的识别出相应的参数。

图1 环形钢丝绳隔振器结构示意图Fig.1 Structural diagram of circular wire-cable vibration isolator
本文针对环形钢丝绳隔振器,提出了一种改进的归一化Bouc-Wen模型,并采用分阶段识别方法基于试验数据对模型参数进行辨识研究。
1 环形钢丝绳隔振器迟滞模型
针对摩擦型迟滞系统,Ikhouane[15]在Bouc-Wen模型基础上提出了归一化Bouc-Wen模型,该模型表述如下:


对于归一化Bouc-Wen模型,选择一组符合各参数条件的组合参数,如图2所示由摩擦力引起的纯迟滞力kωω(t)是有界的,而且在稳定段上界时也就是说纯迟滞力的上界值就是kω,下界值是-kω。

图2 归一化Bouc-Wen模型某一组参数下的纯迟滞力曲线Fig.2 The pure hysteretic curve generated by a set of physically possible parameters of the normalized Bouc-Wen model
根据试验迟滞曲线,如图3所示在垂向承受拉压载荷呈现出非对称迟滞回线,不能直接采用归一化Bouc-Wen模型。为了获得非对称迟滞环,在归一化Bouc-Wen模型中,纯迟滞力乘以一个非线性放大因子,该放大因子可以用一个多项式来表示如下:

式中Fn是非线性放大因子,knj是放大系数,M表示多项式的阶数。
为了准确描述该隔振器非线性弹性刚度,在归一化Bouc-Wen模型中引进非线性弹性恢复力,采用另外一个多项式表示:

式中Fne是非线性弹性恢复力,knei是弹性系数,N表示多项式的阶数。在参数识别时,这两个多项式的阶数和奇偶幂次的确定根据试验数据和理论迟滞环的拟合度指标来选取,通过调节M和N数值的不同,合理选取一种拟合度较好的模型参数。这在参数识别结果和拟合度指标中将会体现出来如表1和2所示。根据试验迟滞特性提出一种改进的归一化Bouc-Wen模型如下:


图3 环形钢丝绳隔振器试验迟滞曲线Fig.3 Experimental hysteresis loop of circular wire-cable vibration isolator
2 环形钢丝绳隔振器模型参数识别
针对式(5)和(6)采用两阶段法进行模型参数辨识。第一阶段先识别非线性弹性恢复力Fne和非线性放大因子Fn;根据识别结果提取由摩擦力引起的纯迟滞响应,在第二阶段识别纯迟滞响应中的各参数。
2.1 阶段1:识别非迟滞参数
如图2所示,由摩擦力引起的纯迟滞响应kωωFn是有界的,当x在稳定段取值时,相对于x轴是对称的,在稳定段恢复力在加载和卸载时分别表示为:

式中fu、fl为环形钢丝绳隔振器在稳定段的上下迟滞恢复力。由于采集的试验数据是离散的,因此式(7)写成离散形式为:

式中下角标k为离散数据第k个点,k取值为1,2,…,K,K为离散数据的长度。先识别Fne的相关参数,由方程(8)可知:

方程(4)写成离散形式为:

式中yik=,kne=[kne1,kne2,…,kneN]是非线性刚度系数矢量,ynek=[y1k,y2k,…,yNk]是线性化变形矢量。误差函数为:

对应的线性最小二乘式为:

采用线性最小二乘法求解方程(12)从而求得非线性刚度系数[kne1,kne2,…,kneN]。
对于非线性放大因子的参数识别采用同样的方法。由方程(8)可知:
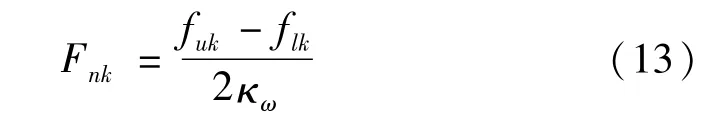
假定在稳定段,x可以取稳定段任意值,为了便于计算,在本程序中x取x(t)在任一周期内的平均值x0。这样可得:
把式(14)代入式(13)可得:

方程(3)写成离散形式为:

式中yjk=,kn=[kn1,kn2,…,knM]是放大系数矢量,ynk=[y1k,y2k,…,yNk]是线性化变形矢量。
采用方程(12)同样的优化方法求得放大系数矢量[kn1,kn2,…,knM]。
2.2 阶段2:识别纯迟滞响应中的各参数
在果蔬病害生物保鲜研究中发现的拮抗细菌主要是芽胞杆菌,其次是假单胞杆菌。芽胞杆菌属好氧或兼性厌氧菌,抗逆能力强,繁殖速度快,营养要求简单,容易定殖在植物表面,适合作为生防制剂。目前,应用于果蔬防腐的有枯草芽胞杆菌、多粘芽胞杆菌和蜡状芽胞杆菌等[6]。
一般情况下,非线性状态变量是无法测量的,然而在许多实际情况下,滞后的极限环可以通过实验得到[8]。由摩擦力引起的纯迟滞极限环响应可由方程(5)求得:
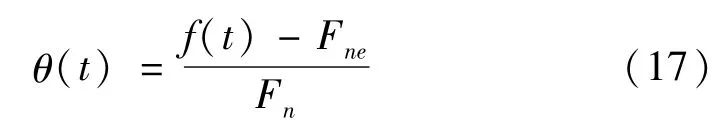
式中θ(t)=kωω是纯迟滞恢复力。由方程(10)和(16)可知,方程(17)写成离散形式为:

采用极限环法[14]识别纯迟滞响应中的各参数。方程(6)写成分段函数为:
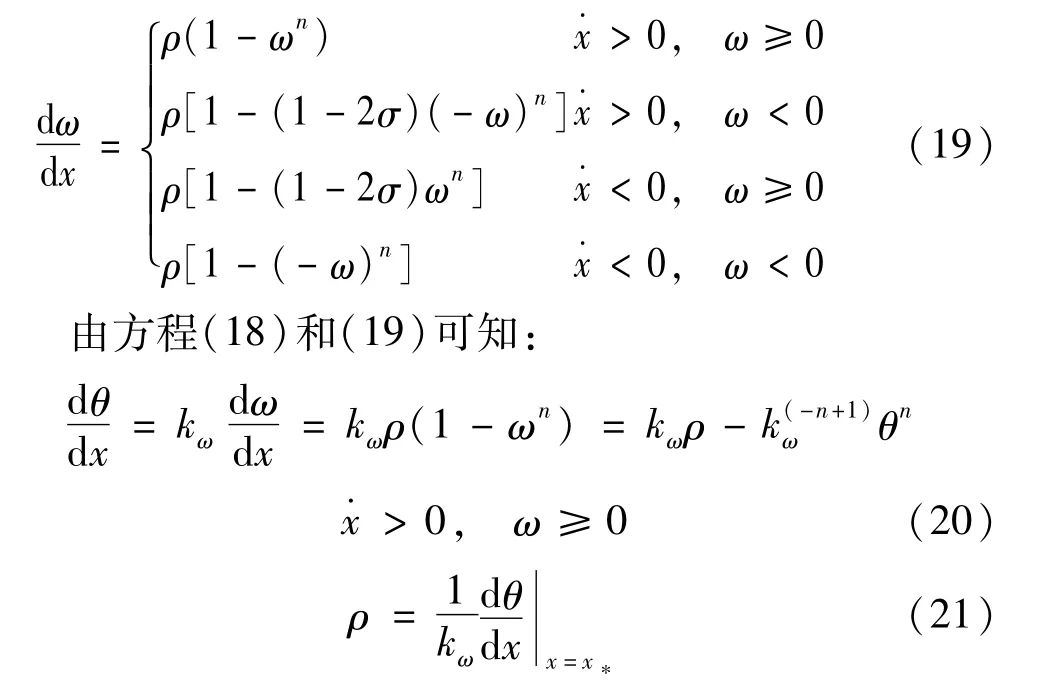
其中:当x=x*时,θ(x*)=0。
纯迟滞响应其余参数的识别由试验数据提取的纯迟滞环的加载曲线求得,如图4所示。假定xm是某一周期内纯迟滞环加载曲线的最小位移值,选取一个点x*1满足条件xm<x*1<x*或者ωx*1<0,另外再取两个点x*3>x*2>x*,把x*2,x*3两个点代入方程(22)可以确定参数n如下式:把x*1点代入方程(19)中x·>0,ω<0时的表达式,可以确定参数σ如下式:
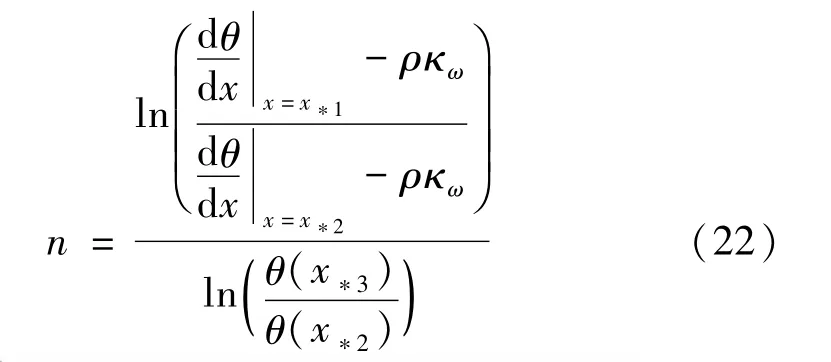
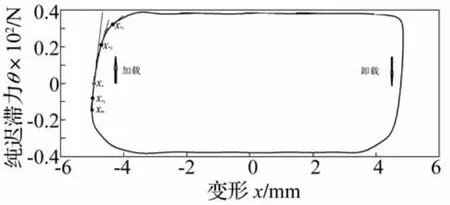
图4 环形钢丝绳隔振器纯迟滞力曲线Fig.4 The pure hysteretic curve of circular wire-cable vibration isolator

2.3 参数识别结果
参照以上各参数识别方法对本研究中的环形钢丝绳隔振器在激励信号为正弦位移,振幅为5 mm,频率为5 Hz,多项式阶数M和N不同时模型参数识别结果如表1所示:

表1 不同多项式阶数M和N模型参数识别结果Tab.1 Model parameter identification results of different polynomial order number M and N
3 动态试验

图5 环形钢丝绳隔振器试验装置Fig.5 Actual setup of circular wire-cable vibration isolator
3.1 试验系统
动态性能测试试验装置如图5所示:该试验是在电磁振动实验台(MPA406/M232)上完成的。隔振器下夹板通过上夹具与三爪卡盘相连。上夹具与力传感器连接,三爪卡盘通过机架与地基相连。隔振器上夹板通过下夹具与电磁振动台体相连,激光位移传感器固定在机架上。恢复力和位移信号同时采集。激励信号采用正弦位移信号,激励幅值在1~5 mm,频率范围3~9 Hz。
该实验采用钢丝绳结构为6X19+IWS,绳圈中径为50 mm,绳圈个数为6,钢丝绳直径为5 mm的钢丝绳环弹性阻尼元件组成的环形钢丝绳隔振器。在隔振器垂向做拉压试验。
3.2 试验数据处理

式中{f}={f0f1f2…和{a}={a0a1a2…是ft和x(t)的谐波分量矢量,ω是激振圆频率,m是傅里叶阶数,根据试验数据选取。当试验采集的数字信号满足一些特定的条件[7]可以采用Ni[13]提出的频域非因果滤波方法对采样数据进行离散傅里叶级数(DFS)高频去噪,求得谐波分量{f},然后重构测量周期信号。
4 模型验证
拟合曲线与试验曲线误差的大小是评价和比较本文提出的环形钢丝绳隔振器预测拟合模型和预测方法的依据。常用的指标是均方根误差(RMSE),表达式如下:

式中pk是拟合曲线离散响应值,fk是试验数据。另外针对非线性模型,张世强[17]提出一个更有效的曲线回归拟合优度指标RNL为:

式中,RNL把残差平方和与相对误差有机地结合在一起,RNL愈接近于1,表示识别参数所拟合的曲线拟合优度愈好。拟合迟滞环与试验迟滞环比较图如图6所示。拟合度指标RMSE和RNL如表2所示。由图6可知,除了在转折点的地方存在差异之外,试验曲线和模型拟合曲线非常吻合。
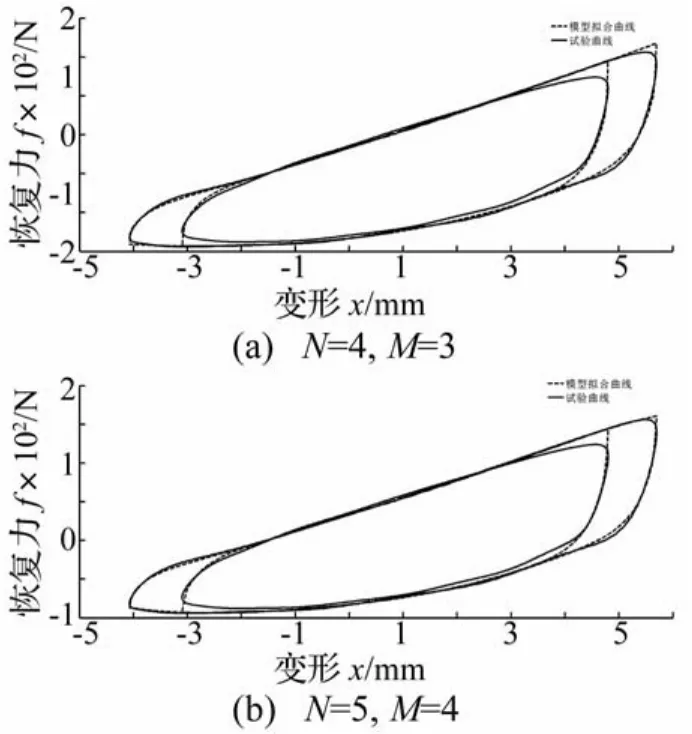
图6 试验和理论拟合迟滞环Fig.6 The measured and predicted hysteresis loops
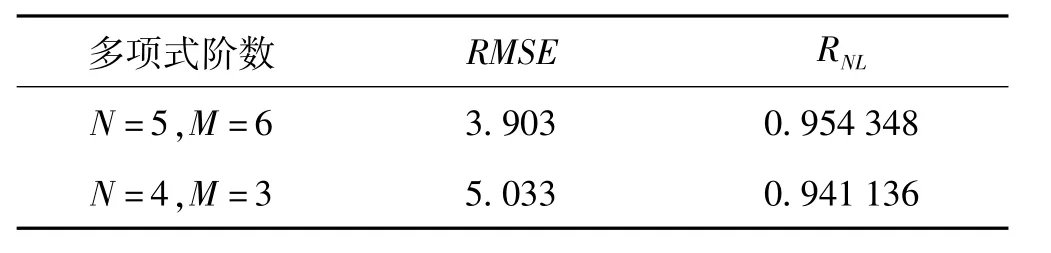
表2 模型拟合迟滞环的拟合度指标RMSE和RNLTab.2 The RMSE and RNLof the predicted hysteresis loops
5 结 论
针对环形钢丝绳隔振器,提出了一种改进的归一化Bouc-Wen模型,并采用两阶段识别方法对模型参数进行辨识研究。同时对模型进行验证,得到主要结论如下:
(1)两阶段识别方法在参数识别过程中不涉及迭代算法,不存在初始参数选取的困扰和收敛性问题,提高了计算效率。
(2)为了模拟非对称迟滞环,引入的两个个多项式的阶数选取不同,模型拟合度不同。基于试验数据合理选择多项式的阶数,可以得到比较理想的拟合效果。
(3)对提出的模型和采用的参数识别方法进行周期性加载试验验证。结果表明:试验曲线和模型拟合曲线吻合的很好。该模型对于环形钢丝绳隔振器垂向非对称迟滞环的动态特性的描述是准确和有效的。为建立环形钢丝绳隔振器动态设计方法以及下一步研究环形绳圈弹性阻尼元件结构参数对其刚度和阻尼的影响奠定了基础。
[1]Demetriades G F,Constantinou M C,Reinhorn A M.Study of wire rope systems for seismic protection of equipment in buildings[J].Engng Structs,1993,15:321-334.
[2]LeKuchH.Shockandvibrationisolationinsevere environments[J].Noise Vibration Control Worldwide,1986,17:240-245.
[3]束立红,周炜,吕志强,等.钢丝绳隔振器在大型机械设备的振动冲击隔离设计中的应用[J].振动与冲击,2006,25(4):78-81.
SHU Li-hong,ZHOU Wei,LÜ Zhi-qiang,et al.Stainless steel wire-rope isolator used in vibration and impact isolation design for large machine equipment[J].Journal of vibration and shock,2006,25(4):78-81.
[4]向红,吴若梅.钢丝绳隔振器在运输包装中的应用研究[J].湖南大学学报,2002,29(3):65-67.
XIANG Hong,WU Ruo-mei.Study of application of wire cable vibration isolator in fields of transport packaging[J].Journal of Hunan University,2002,29(3):65-67.
[5]Cutchins M A,Cochran J E,Guest S,et al.An investigation of the damping phenomena in wire rope isolators[C].The Role of Damping in Vibration and Noise Control ASME DE-5,1987:197-204.
[6]Tinker M L,Cutchins M A.Damping phenomena in a wire rope vibration isolation system[J].Journal of Sound and Vibration,1992,157(1):7-18.
[7]Ko J M,Ni Y Q,Tian Q L.Hysteretic behavior and empirical modeling of a wire-cable vibration isolator[J].The International Journal of Analytical and Experimental Modal Analysis,1992,7(2):111-127.
[8]Ni Y Q,Ko J M,Wong C W.Identification of non-linear hysteretic isolators from periodic vibration tests[J].Journal of Sound and Vibration,1998,217(4):737-756.
[9]胡海岩,李岳峰.具有记忆特性的非线性减振器参数识别[J].振动工程学报,1989,2(2):17-27.
HU Hai-yan,LIYue-feng.Parametricidentificationof nonlinear vibration isolators with memory[J].Journal of Vibration Engineering,1989,2(2):17-26.
[10]BoucR.Forcedvibrationofmechanicalsystemswith hysteresis[C].Proceedings of the 4th Conference on Nonlinear Oscillations,Prague,1967.
[11]Wen Y K.Method for random vibration of hysteretic systems [J].Journal of the Engineering Mechanics Division,1976,102(2):249-263.
[12]Ni Y Q,Ko J M,Wong C W,et al.Modelling and identification of a wire-cable vibration isolator via a cyclic loading test,Part 1:Experiments and model development [J].Proceedings of the Institution of Mechanical Engineers,Part I-Journal of Systems and Control Engineering,1999,213 (3):163-171.
[13]Ni Y Q,Ko J M,Wong C W,et al.Modelling and identification of a wire-cable vibration isolator via a cyclic loading test Part 2:identification and response prediction[J]Proceedings of the Institution of Mechanical Engineers,Part I-Journal of Systems and Control Engineering,1999,213(3):173-182.
[14]Ikhouane F,Gomis-Bellmunt O.A limit cycle approach for the parametric identification of hysteretic systems[J].Systems&Control Letters,2008,57(8):663-669.
[15]Ikhouane F,Rodellar J.On the hysteretic Bouc-Wen model-Part I:Forced limit cycle characterization[J].Nonlinear Dynamics,2005,42(1):63-78.
[16]Ikhouane F,Manosa V,Rodellar J.Dynamic properties of the hysteretic bouc-wen model[J].Systems&Control Letters,2007,56(3):197-205.
[17]张世强.曲线回归的拟合优度指标的探讨[J].中国卫生统计,2002,19(1):9-11.
ZHANG Shi-qiang.Approach on the fitting optimization index of curve regression[J].Chinese Journal of Health Statistics,2002,19(1):9-11.
Modeling and parametric identification for dynamic behavior of a circular wire-cable vibration isolator
WANG Hong-xia1,2,3,GONG Xian-sheng1,2,LIU Wei1,2,PAN Fei1,2
(1.State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400044,China;2.College of Mechanical Engineering,Chongqing University,Chongqing 400044,China;3.Hubei Automotive Industrial Institute,Shiyan 442002,China)
A circular wire-cable vibration isolator was designed by adopting independent wire rope loops as elastic damping elements.Owing to its unique structure,the isolator exhibited nonlinear elastic stiffness and dynamic behavior of asymmetric hysteresis in its tension compression mode.In the present study,a modified normalized Bouc-Wen model was proposed to describe the hysteretic behaviour of a circular wire-cable vibration isolator.A two-stage identification method was developed for identifying its modal parameters.Periodic loading tests were conducted to validate the proposed model and identification method.The results showed that the proposed model and identification method are effective for accurate description of asymmetric hysteretic dynamic behavior in the tension compression mode of circular wire-cable vibration isolator.The results laid a foundation for dynamic design method of circular wire-cable vibration isolators.
circular wire-cable vibration isolator;hysteresis;modified normalized Bouc-Wen model;identification
TU112
A
10.13465/j.cnki.jvs.2014.23.010
国家自然科学基金(51175525);973资助项目(2014CB049403);湖北汽车工业学院博士基金(BK201406);重庆大学机械传动国家重点实验室自主研究基金(0301002109137)
2013-08-20 修改稿收到日期:2013-12-12
王红霞女,博士生,讲师,1977年12月生
龚宪生男,教授,博士生导师,1956年生

