VMI环境下库存竞争性产品的补货策略及最优货架空间的确定

杨建功，卿前龙

（广东金融学院休闲产业与高端服务业研究中心，广东广州 510521）

VMI环境下库存竞争性产品的补货策略及最优货架空间的确定

杨建功，卿前龙

（广东金融学院休闲产业与高端服务业研究中心，广东广州 510521）

本文在文献［1］的研究基础上，通过深入剖析FKO模型，运用动态规划方法，探讨了呈现特殊需求性质的库存竞争性产品在VMI环境下的多期动态补货策略，以及传统库存管理中不加考虑的库存空间优化问题。本文一方面是对FKO模型的补充与扩展，同时也证实了对于在特定的VMI补货环境下采用多期库存盘查模式的供应商来说，封顶式的补货策略是最优的，并且其关于最优补货水平的多期决策都是无远见的。因此收益分享合同下的单期最优库存水平可以作为设定最优货架展示空间的依据。

VMI；库存竞争性产品；补货策略；最优货架空间

1 引言

市场中存在一类产品，其特点就是该产品摆放在货架上的数量越多，需求就越旺盛。在过往的文献中一般把这类产品称之为外部需求依赖展示库存（shelf-space dependent demand）的产品，例如生鲜食品市场中的蔬菜水果，鱼类、蛋类，肉类产品等都具有如此特点。因为该类产品需求随库存量变化而随机波动，相对于通常经济学意义上的价格导致需求波动的价格竞争性产品，笔者将这类产品称之为库存竞争性产品。

国内外许多学者从不同侧面，就库存竞争性产品的供应链系统进行了相关的建模研究，如罗兵等人［2-3］，Gerchak和Wang Yunzong［4-6］，Pal等人［7］，Padmanabhan和Vrat［8］，Giri等［9］，Balakrishnan等人［10］，Giri和Chaudhuri［11］，Zhou Yongwu和Yang Shanlin［12］。其中，以Gerchak和Wang Yunzeng［4-6］的一系列研究工作最为深入，他们针对库存竞争性产品所提出的需求模型和订货策略成为本文的研究基础。而VMI（Vendor Managed Inventory，即供应商管理库存）作为一种新的供应链合作关系，正受到企业界和理论界的高度重视。目前对VMI的研究主要集中在动态的生产和补货策略［13］，供应链绩效评价［14-15］，VMI环境下的品牌竞争［16］，以及库存和运输决策［17］等问题。

在杨建功等［1］文献中，笔者通过对VMI环境下库存竞争性产品的收益分享合同的研究，引出两个值得关注的问题：

（1）供应商在VMI环境下向零售商的补货策略是什么？

（2）VMI环境下，如何确定零售商端的最优货架展示空间？

为了解决上述两个问题，有必要参照Fry，Kapuscinski和Olsen［13］的研究思路和相关成果。Fry，Kapus-cinski和Olsen［13］提出的（z，Z）式VMI合同下的随机动态多期生产与补货策略模型，可称之为Fry-Kapuscinski-Olsen模型（简称为FKO模型）。

利用该模型，Fry等人［13］得到的主要结论是：在许多方面（尤其是当外购成本相当高的情形下），（z，Z）式VMI合同下的供应链绩效水平都显著优于传统供应链库存管理方式（RMI），但也在其它一些方面，其表现却不尽人意，其原因就在于VMI环境下的供应商承担了额外的供应链管理与库存成本。

借鉴FKO模型，本文将运用动态规划方法，就库存竞争性产品在VMI环境下的多期动态补货策略进行建模研究，主要得到两个结论：（1）对于在特定的VMI补货环境下采用多期库存盘查模式的供应商来说，封顶式的补货策略是最优的，并且其关于最优补货水平的多期决策都是无远见的（myopic）；（2）库存竞争性产品收益分享合同下的单期最优库存水平，可以作为设定最优货架展示空间的依据。

2 建模及分析

2.1 基本框架和参数说明

考虑供应商的补货能力，我们将设定两种补货环境—开放系统和封闭系统。如前所述，供应商具有库存竞争性产品的生产能力，但还可以通过外购途径获取该产品，以便向下游零售商及时补货，但外购成本要高于自产成本。假定供应商在一个离散的库存消耗期之初只安排一次生产计划，如果在VMI环境下，供应链系统处于第n阶段，n=1，2，3…，T -1，供应商的在手库存消耗完毕，在下一轮生产计划尚未实施之前，以较高的成本外购库存竞争性产品是供应商向零商端进行补货的唯一选择，我们把这种条件下的补货环境称之为“开放式”的，以强调供应商的补货货源来自二级供应链的外部，属于外购能力；相对应地，当供应商阶段的在手库存大于零时，供应商基于补货成本的考虑，只会从自身的在手库存中向零售商端的货架空间进行补货，我们把这样的补货环境称之为“封闭式”的，以强调供应商的补货货源来自二级供应链的内部，属于自产能力。

同时，继续沿用杨建功等［1］提出的收益分享合同模型。因此，在一定程度上说，供应商与零售商之间仍是Stackelberg博弈关系，供应商关心自身收益最大化条件下的最优多期补货水平，零售商关心自身收益最大化条件下的收益分配系数，但本文的研究重点集中于供应商的决策行为，对零售商的博弈行为暂时不予考虑。

除了杨建功等［1］引入的相关模型参数外，本文中还要用到以下参数：

xR：单期静态库存管理下，零售商的初始库存，xR≥0；

xS：单期静态库存管理下，供应商的初始库存，xS≥0；

2.2 开放系统的补货策略

VMI环境下，供应商在一个离散的库存消耗期的开始之初只安排一次生产计划，如果供应链系统处于第n阶段，n=1，2，3…，T-1，供应商的在手库存消耗完毕，即当=0时，那么在下一轮生产计划尚未实施之前，供应商不得不从系统外以较高的采购成本c0订购库存竞争性产品以应对零售商端在剩余各阶段n+1，n+2，…，T-1内不断到达的随机需求。由于供应商不持有库存，库存状态的动态演化只在零售商端进行，系统状态方程如下：

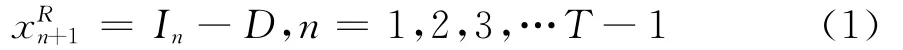
系统方程（1）式反映了先前对需求函数的假定，即每阶段的随机需求均为恒定分布，独立于n。此时在采用收益分享合同的前提下，供应商的单期期望收益函数为：

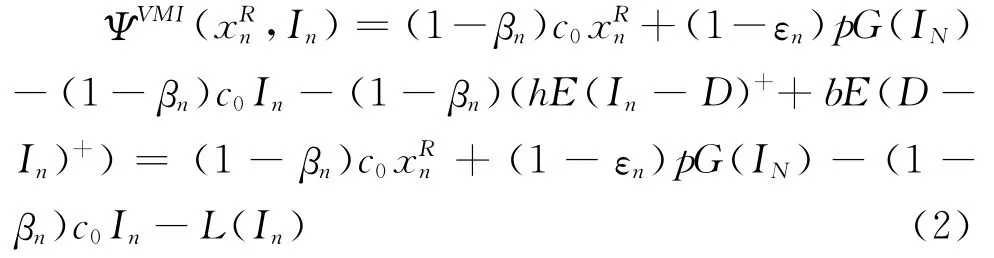
其中，L（In）=（1-βn）（hE（In-D）++bE（D -In）+）为供应商应当承担的期望库存持有和拖后交货成本。0≤εn＜1，0≤βn≤1为第n阶段的供应链收益分享系数和成本分担系数。

由系统方程式（1），可知xRT作为T周期末的剩余库存量，如果为正，就是整个T周期的积余库存；如果为负，就是未满足的客户需求，其持有和拖后交货成本都反映在第T-1阶段的期望收益函数ψVMI（-1，IT-1）当中，除此之外还假定T周期末的剩余库存＞0的价值为0。由此，在不考虑折扣因素的前提下，可得供应商在整个T周期内的总期望收益的表达式：

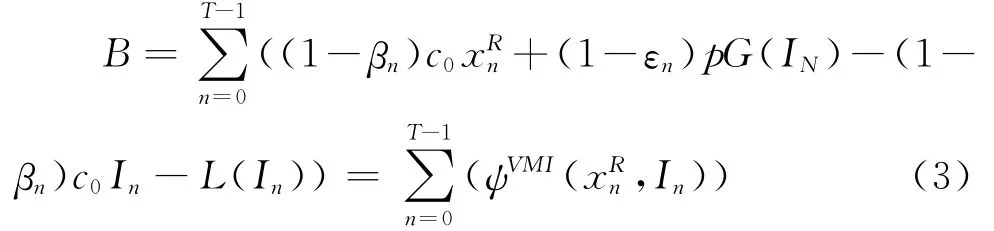
供应商的决策目标是最大化B，这等同于求解下列的动态规划方程：

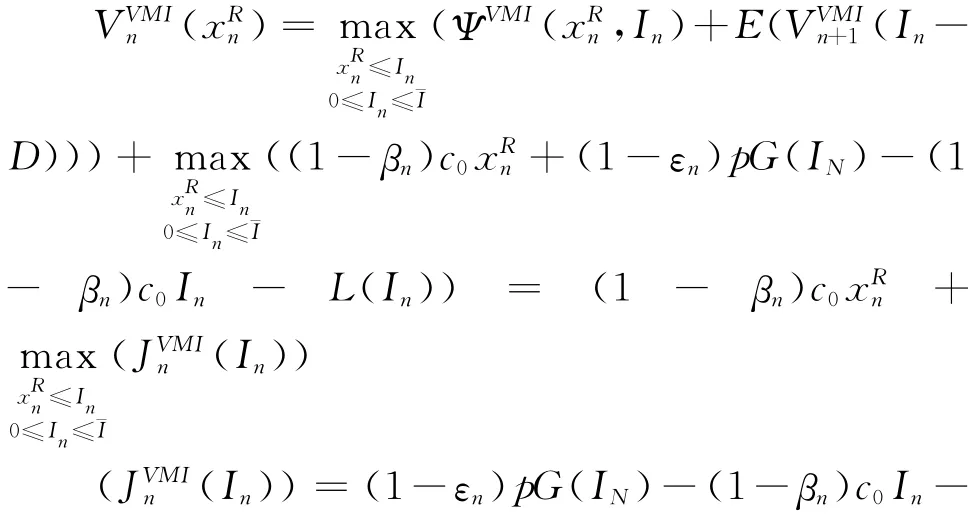
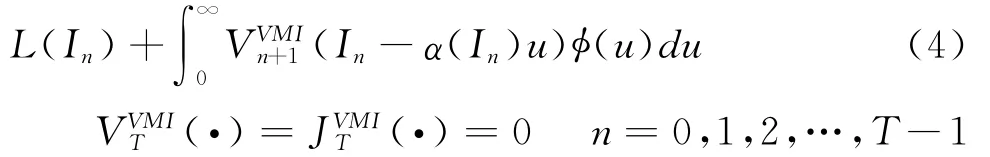
相对于总期望收益最大化的决策目标，本文更关心供应商的补货策略及其最优性，以及最优补货控制序列｛I*n｝的特点，因此，本文将侧重于动态规划方程（4）的分析与研究，其关键是要证明（4）式所表达的动态规划算法确实能够的到一个最优的补货控制序列｛I｝，使得函数JVMIn（In）最大化，即存在以下封顶式的补货策略：

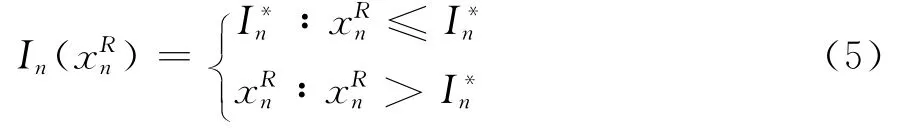
为了证明策略式（5）的最优性，需先给出如下一个推论和一个引理，但首先需要明确以下假设条件：

假设1 对任何x≥0，u≥0都有：

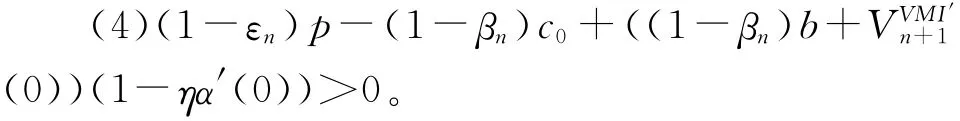
推论1 对库存竞争性产品采用多期库存盘查模式，各阶段的随机需求分布恒定，独立于n，存在：

（1）当需求扰动因子ξ的分布具有IFR（increasing failure rate）性质时，期望库存持有和拖后交货成本函数L（In）是关于In的凸函数，且L′（0）=-（1-βn）b（1-ηκ′（0）），L′（∞）=（1-βn）h；

（2）期望销售函数G（In）为关于In的正的严格递增凹函数，即有G（In）＞0，G′（In）＞0，G″（In）＜0，且G′（0）=1，G′（∞）⇒0。

证明 在随机需求恒定分布的前提下，根据库存竞争性产品的需求模型有关性质，由杨建功［1］中的引理1和引理2即可得出上述推论。L（In）的凸性与G（In）的凹性证明过程从略，其他性质证明如下：

由库存竞争性产品的需求模型有关性质可知：

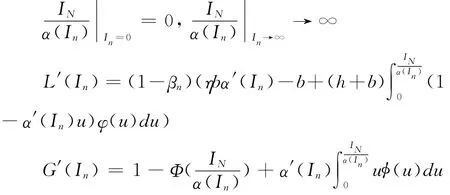
因此有：

L′（0）=-（1-βn）b（1-ηκ′（0）），L′（∞）=（1 -βn）h；G′（0）=1，G′（∞）⇒0 证毕。

推论1中的性质G′（∞）⇒0再次验证，将库存大量囤积于零售商端的展示货架上并不能无限提高产品的销售率。

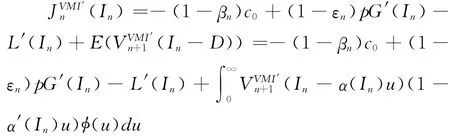
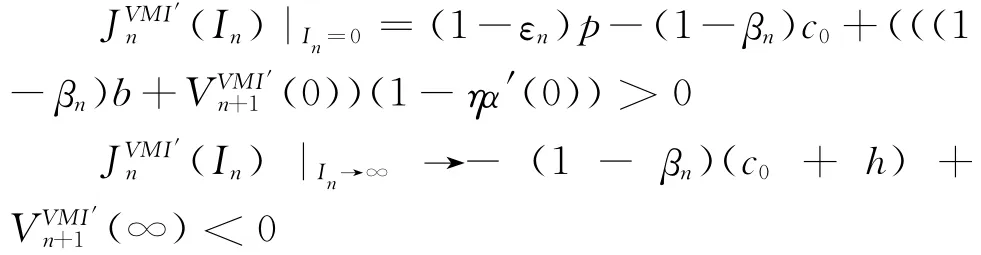
在上述一系列假设和引理的基础之上，可得到如下命题：

命题1 在一个采用VMI收益分享合同的供应商-零售商式二级供应链中，当供应商第n=0，1，2，…，T-1阶段的库存竞争性产品在手库存为零，即=0，而新的生产计划尚未开始实施之际，供应商只能通过外购获取产品，以便向零售商及时补货。此时，供应商在自身收益最大化的前提下所采取的封顶式补货策略是最优的。

证明 该命题的证明等价于策略式（5）的最优性证明，关键是通过归纳法确定V（x），n=0，1，2，…，T-1是关于的连续凹函数，且有，并且对任何x≥0，u≥0，在x的某临域内，函数关于x的二阶导数。对于T-1阶段，由可得：

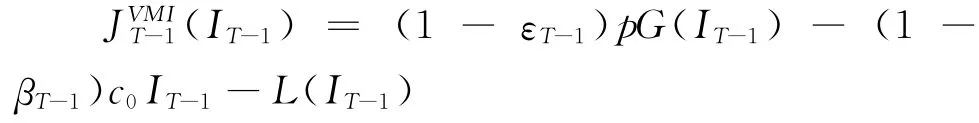
由引理1可知存在唯一I*T-1使得JVMIT-1（I）最大，根据（4）与（5）式可得：

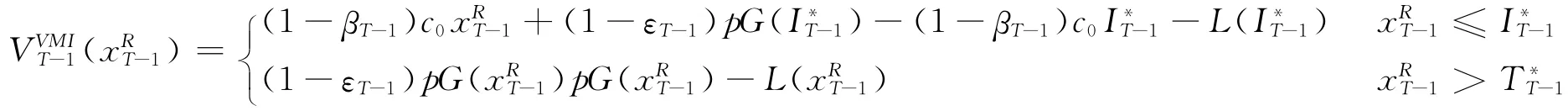
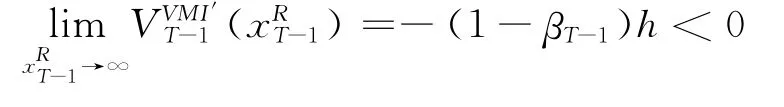
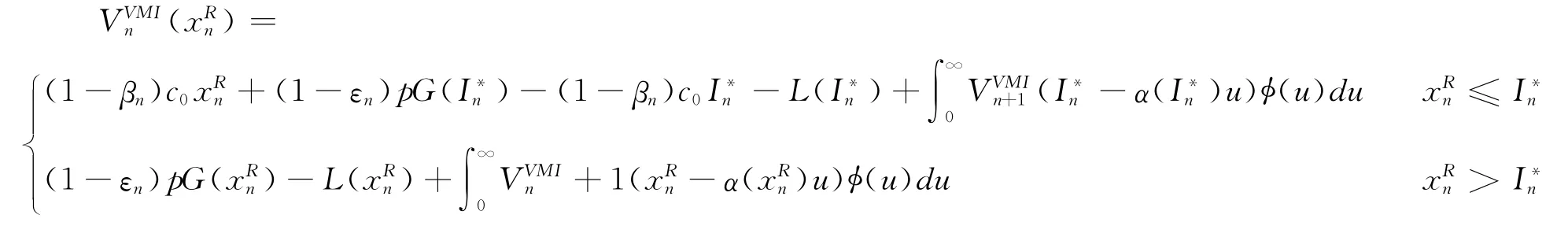
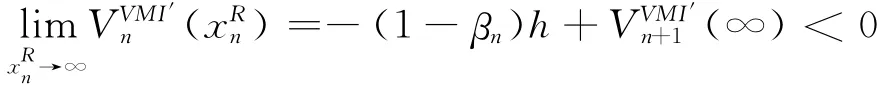
而根据假设1之条件2，当x-κ（x）u＞I*n时，有：

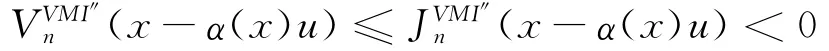
策略式（5）的最优性得到证明。

证毕。

从以上分析过程中，可以看到假设1中条件2与3之必要性。为了证明补货策略的最优性，虽然的凹性前提是必要的，这在T-1阶段或单期模型中已经体现出来，但根据系统的状态方程，在n=T-2，…，0时，上一阶段关于的凹函数，并不能保证下一阶段V（In-κ（In）ξ）是关于In的凹函数。这完全是由库存竞争性产品的需求模型的特点所决定的，假设1之有关限定条件就是要保证每阶段的递推方程都是关于库存最高补货水平In的凹函数。

2.3 开放系统的补货策略

在VMI环境下，当供应商第n=0，1，2，…，T-1阶段的在手库存大于零时，即xs＞0，基于补货成本的考虑他只从自身的在手库存向零售商补货。如前所述，我们把此时的供应链补货环境称之为封闭系统，即补货行为是在供应链“内部”进行的。此时的供应链库存状态的动态演化就不仅仅只在零售商端进行，同时还要考虑整个供应链的库存，也就是级库存的状态变化，此时的系统状态方程为：

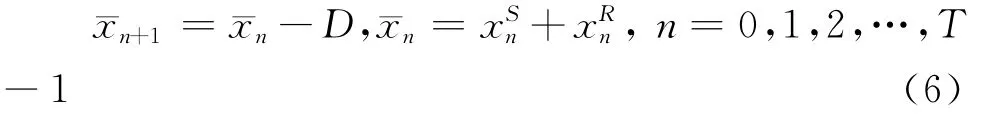
之所以考虑整个供应链级库存状态变化是因为此时供应商向零售商端补货的最优封顶式补货量，n=0，1，2，…，T-1，除了天然的约束条件0＜≤¯I外，此时还要受到如下限制：

即供应商补货后的零售商端库存水平最高不能超过当期的供应链级库存水平。在采用收益分享合同的前提下，供应商第n阶段的单期期望收益函数为：

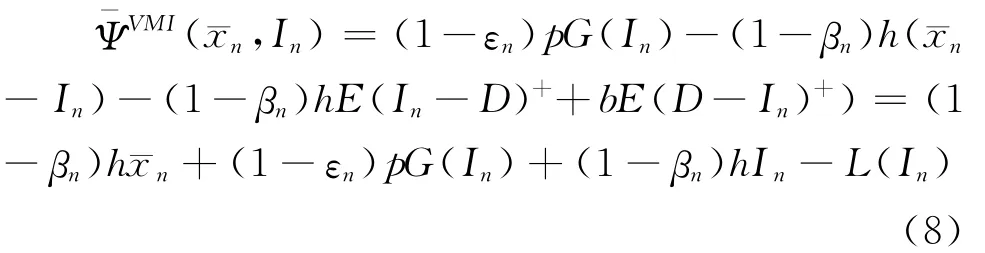
在封闭的、没有生产和外购行为发生的这个简单的二级库存供应链系统中，供应商的销售收入决定于外部市场，与开放系统相比没有任何改变，但其成本结构却有所不同，要承担成部分供应链级库存的持有成本，以及需求过后的部分库存持有和拖后交货成本。

与前文一样，假定第T阶段的供应链级库存¯xT＞0的积余价值为0，在不考虑折扣因素的前提下，可得供应商在整个T周期内的总期望收益的表达式：

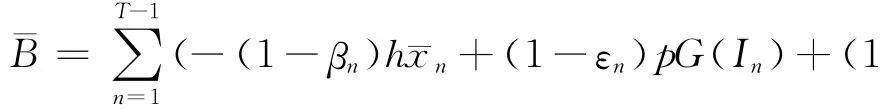
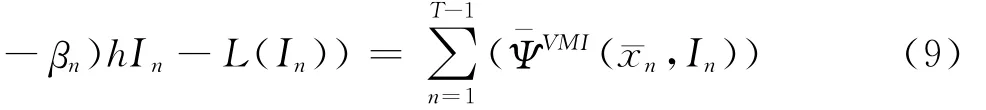
供应商的补货类型仍然属于封顶式的，其目标也是寻求从第n阶段开始到T阶段结束，n=0，1，2，…，T-1，也就是下一个生产周期开始之前的一个最优的补货控制序列｛｝，其前提就是使得自身的总期望收益¯B最大化，这等同于求解下列动态规划方程：

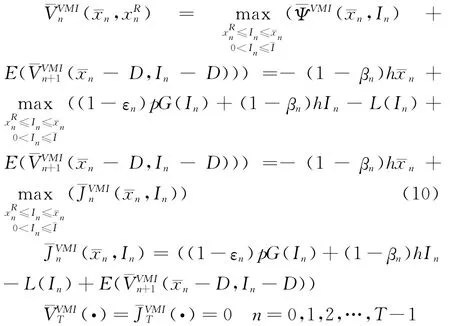
如果不考虑供应链级库存状态，将零售商端的库存状态演化过程独立出来，会存在与（4）式相对应的一组动态规划方程：

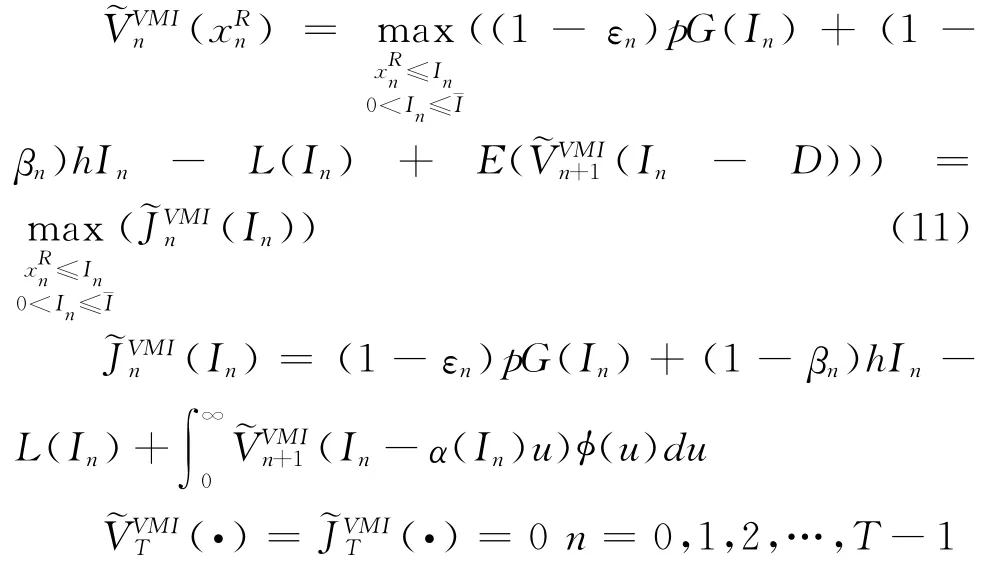
对于（11）式，同样有：

假设2 对任何x≥0，u≥0都有：

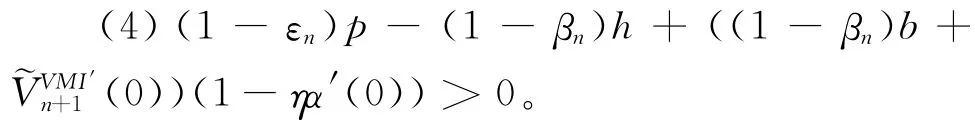
引理2的证明方法和过程可参照引理1，此处从略。

假设3 对任何x≥0，u≥0：

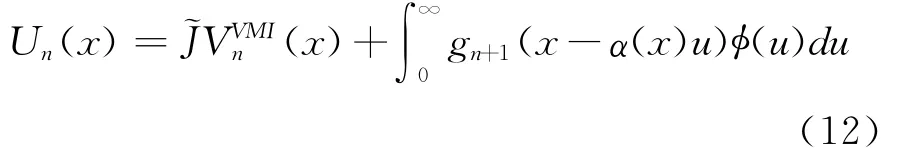
基于以上假设，则有如下引理：

引理3

证明 对于（1），将运用归纳法进行证明：

该结论对于T-2阶段显然是成立的，而在n= T-3，…，0时，先假设该结论对于n+1阶段成立，即当使得）达到最大化时有：

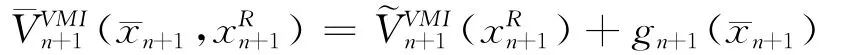
随后将证明该结论对于n阶段也成立。由上式可得：

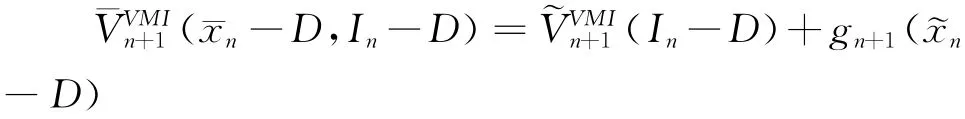
代入（10）式后可得：

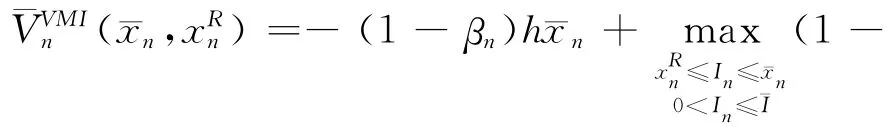
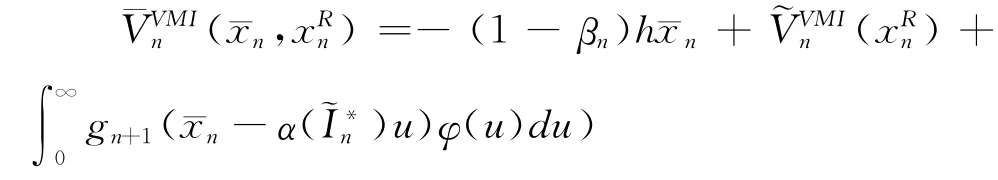
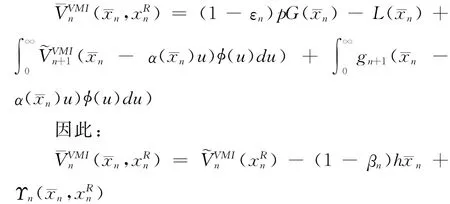
其中：

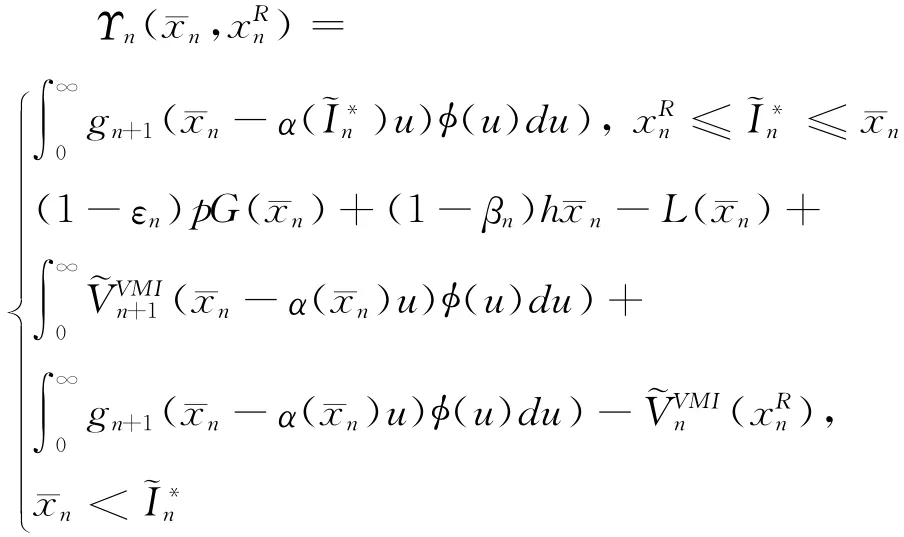
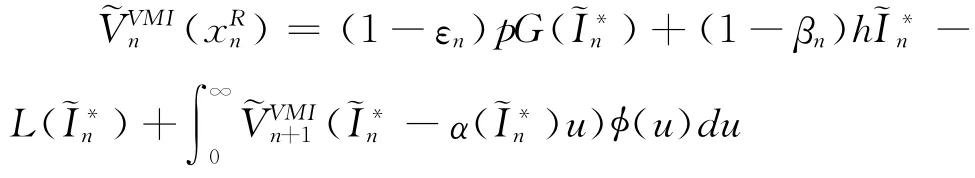
进而：

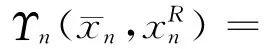
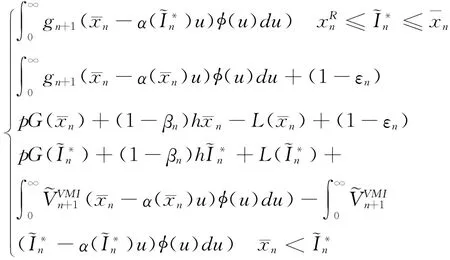
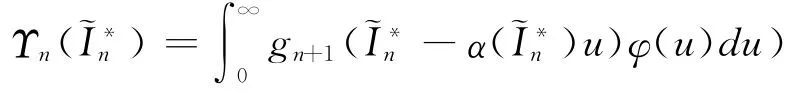
所以Υn（，）是一个仅与∈［，∞）相关的连续函数，在此可另记作Υn（¯xn）。根据引理2及相关前提，Υn）的凹性是显而易见的。进一步由假设3条件2中的公式（13）及相关前提，可知对于任何x≥0，u≥0，函数Υn（x-κ（x）u）关于x的二阶导数小于0，Υ″n（x-κ（x）u）＜0，因此对于gn（x）=Υn（x）-（1-βn）hx不仅是关于x的连续凹函数，而且也存在：

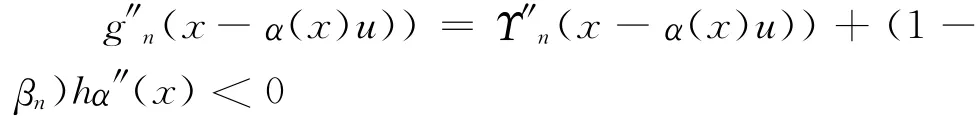
至此，引理之第（1）部分得证。对于（2），基于假设3之条件2，以及函数序列｛gn（）｝的一系列性质，其证明过程（1）的证明过程相类似，也可参照命题1，故而从略。因而，最优封顶式补货水平序列｛｝存在，策略式（12）是最优的。

证毕。

在引理3的基础之上，可以立即得到如下命题：

命题2 在一个采用VMI收益分享合同的供应商-零售商式二级供应链中，当供应商第n=0，1，2，…，T-1阶段的库存竞争性产品在手库存大于零，即x＞0，那么在新的生产计划尚未开始实施之前，供应商更愿意通过在手库存向零售商及时补货。此时，供应商在自身收益最大化的前提下所采取的封顶式补货策略是最优的。最优控制系列｛｝，n =0，1，2，…，T-2，可以通过（11）式近似求得，和之间存在如下关系：

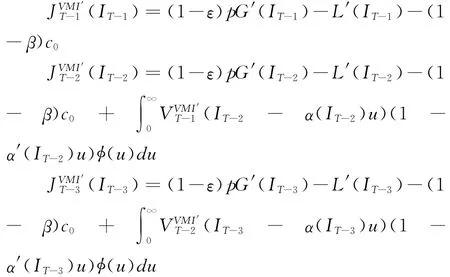
以上针对一个VMI环境下经营库存竞争性产品的简单二级供应链，在有限时间水平下，两种补货系统中的多期动态补货策略进行了分析和研究。接下来需要面对的问题就是如何确定最优的库存展示空间。那么就需要对两种系统下的最优补货封顶值的特点进行深入的分析和研究。但首先要假设系统所采用的VMI收益分享合同各阶段的收益分享系数εn和成本分担系数βn都相等，即ε0=ε1=ε2=…=εT-1=ε，β0=β1=β2=…βT-1=β。

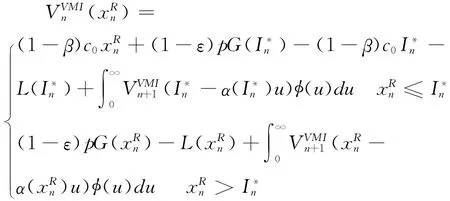
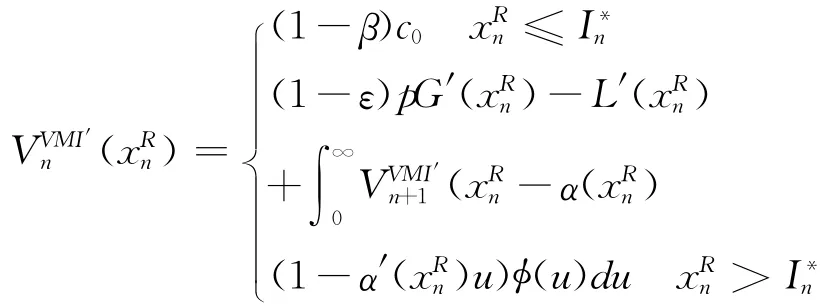
从上述分析过程中，可以看出（1-β）c0是）一阶导数的上确界，即对所有，都有，因而对于n=T-2，…，0：

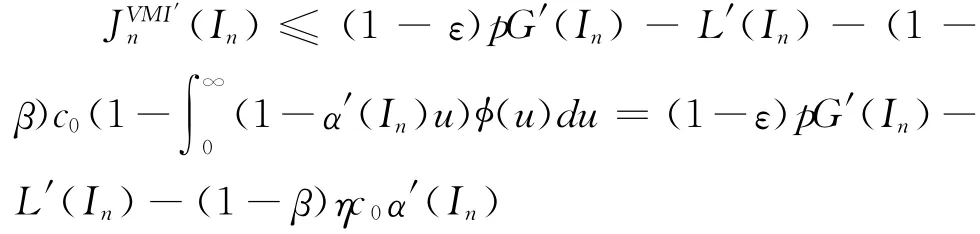
显然，当ηκ′（In）≥1时，，∀n=T-2，…，0，。至此，可以得到如下引理：

引理4 在命题1所描述的开放系统中：

（2）当ηκ′（In）≥1时，，∀n=0，1，2，…，T-2；

（3）系统在n=0，1，2，…，T-2阶段的最优补货封顶值依次递减，即：。

此引理的证明方法和过程可参照上述分析，此处从略。

结论1 当ηκ′（In）≥1时，在开放系统中，供应商可依据期末的最优补货封顶值I来确定库存竞争性产品的最优货架展示空间，=。

引理4与结论1显示，虽然有可靠的外部货源作为及时补货的保证，但出于采购成本的考虑和供应商本身具有生产能力，总期望收益最大化的决策目标约束下，供应商会在下次生产计划实施前的剩余各阶段逐步减少最优补货封顶值，但在最终的期末T-1阶段这一最优值却是各阶段中的最大值。库存竞争性产品的需求特点是唯一可以解释这一现象的原因。

但对于供应商来说这是一个再好不过的结论，因为这是一个无远见（myopic）决策，他只需在单期的期望收益最大化的条件下，就可以确定最优货架展示空间了，简单地说，只要解一个关于I的方程就可以了：

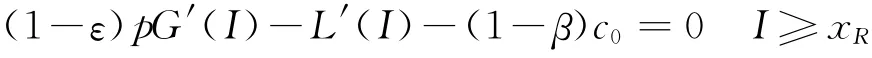
但出于现实条件考虑，采用各最优封顶补货值的中位数作为最优货架空间，然后在剩余各期中使货架空间处于满负荷状态，似乎是一种可行的折衷方法。

对于封闭系统，有如下引理：

引理5 在命题2所描述的封闭系统中，各期最优补货封顶值近似于，而独立于n=0，1，2，…，T-1，即有

此引理由（11）式不难得到证明，故其证明方法和过程从略。

毫无疑问，在封闭系统中，最优补货封项值与最优货架空间在各阶段保持完美的一致性，并且二者都是无远见决策，都是以下关于I的方程的解：

（1-ε）pG′（I）-L′（I）+（1-β）h=0 xR≤I≤¯x

其中¯x为封闭系统的级库存。这是供应链双方都满意的一个最优的结果。考虑到供应商的初始在手库存为零是一个非常理论化的假设，而供应商又具有生产能力，那么供应商在现实中的补货决策大多都是在其在手库存不为零的条件下进行的，这一结果具有一定的现实参考意义。

引理6 当ηκ′（In）≥1时，两系统最优补货封顶值之间存在如下关系，∀n=0，1，2，…，T-1。

根据引理4，此引理不难证明，故其证明方法和过程从略。

结论3 如果供应商在不同的离散库存消耗期Γk内，Γk=0，1，2，…，T，k=0，1，2，…，分别处于上述两种不同的供应链系统中，那么，就是供应商要确定的最优的货架展示空间。

3 结语

通过以上对库存竞争性产品在VMI收益分享合同下的多期补货策略的研究，本文开始提出的两个问题得以解决，基本上排除了这样的担忧，即：收益分享合同下的单期最优库存水平可能无法作为设定最优货架展示空间的依据。可以发现即使供应商是一个长远目标的制定者，但其决策结果却仍然是“无远见”的，供应商单期收益最大化决策下所得到的库存控制目标，在更长期的库存管理阶段内依然是最优的。

这一结果和Gerchak与Wang Yunzeng［4-6］基本一致，所不同的是本文的供应链采用了非传统的VMI集成机制，并设定了两类不同的补货环境，充分考虑了供应商本身的供货能力。虽然基本思路受到FKO模型的启发，但由于库存竞争性产品需求模型的特殊性，其结果与FKO模型存在相当多的不同，例如封闭系统的补货策略，以及开放系统的最优补货封顶值的排列方式等。

本文的研究工作与文献1有密切的联系，由于所采用的“供应商—零售商”式的二级供应链是基本的二元博弈结构，本文的研究工作在未来还有进一步扩展的空问，例如供应商的最优生产策略，零售商的多期决策行为（如收益分享系数的确定）等。笔者将在今后的研究工作中做进一步的探索和努力。

［1］杨建功，王国庆.库存竞争性产品的VMI收益分享合同模型［J］.系统工程理论与实践，2009，29（6）：46-58.

［2］罗兵，熊中楷，杨秀苔.存货影响销售率且理论需求为线性时变函数时的EOQ模型［J］.中国管理科学，2002，10（6）：66-71.

［3］罗兵，杨帅，熊中楷.短缺量拖后率、需求和采购价均为时变的变质物品EOQ模型［J］.中国管理科学，2005，13（3）：44-49.

［4］Gerchak Y，Wang Yunzeng.Periodic-review inventory models with inventory-level-dependent demand［J］.Naval Research Logistics，1994，41（1）：99-116.

［5］Wang Yunzeng，Gerchak Y.Supply chain coordination when demand is shelf-space dependent［J］.Manufacturing&Service Management，2001，3（1）：82-87.

［6］Wang Yunzeng，Gerchak Y.Supply chain contracting and coordination with shelf-space-dependent demand［M］.Joseph G，Pardalos P M，Edwin R H.Supply Chain Management：Models，Applications and Research Direction.Netherlands：Kluwer Academic Publishers，2002.

［7］Pal S，Goswami A，Chaudhuri K S.Deterministic inventory model for deteriorating items with stock-dependent demand rate［J］.International Journal of Production Economics，1993，32（3）：219-299.

［8］Padmanabhan G，Vrat P.EOQ models for perishable items under stock dependent selling rate［J］.European Journal of Operational Research，1995，86（2）：281-292.

［9］Giri B C，Goswami A，Chaudhuri K S.An inventory model for deteriorating items with stock-dependent demand rate［J］.European Journal of Operational Research，1996，95（3）：604-610.

［10］Balakrishnan A，Pangburn M S，Stavrulaki E.＂Stack them high，let'em fly＂：Lot sizing policies when inventories stimulate demand［J］.Management Science，2004，50（5）：630-644.

［11］Giri B C，Chaudhuri K S.Deterministic models of perishable inventory with stock-dependent demand rate and nonlinear holding cost［J］.European Journal of Operational Research，1998，105（3）：467-474.

［12］Zhou Yongwu，Yang Shanlin.An optimal replenishment policy for items with inventory-level-dependent demand and fixed lifetime under the LIFO policy［J］. Journal of the Operational Research Society，2003，54：585-593.

［13］Fry M J，Kapuscinski R，Olsen T L.Coordinating production and delivery under a（z；Z）-type vendormanaged inventory contract［J］.Manufacturing& Service Operations Management，2001，3（2）151-173.

［14］Yao Yuliang，Evers P T，Dresner M E.Supply chain integration in vendor-managed inventory［J］.Decision Support Systems，2007，43（2）：663-674.

［15］Dong Yan，Xu Kefeng.A supply chain model of vendor managed inventory［J］.Transportation Research，2002，38（2）：75-95.

［16］Mishra B K，Raghunathan S.Retailer-vs.vendormanaged inventory and brand competition［J］.Management Science，2004，50（4）：445-457.

［17］Cetinkaya S，Lee C Y.Stock replenishment and shipment scheduling for vendor-managed inventory systems［J］.Management Science，2000，46（2）217-232.

The Replenishment Policy and Optimal Shelf Space of the Inventory Competitive Product Under VMI

YANG Jian-gong，QING Qian-long
（The Center for Leisure and Service Research，Guangdong University of Finance，Guangzhou 510521，China）

Based on previous research［1］，by analyzing FKO model and taking the inventory competitive product（ICP）'s demand nature into consider，an appropriate model is built by using the dynamic programming method to determine the optimal shelf space which has never been considered in the traditional system.Chone hand，the optimality of supplier's multiperiod dynamic replenishment policy under VMIis verified，which to some extent develops the FKO model.On the other hand，it can be learnt that it is optimal for the ICP supplier to follow a replenishment-up-to policy under different VMI environments by a periodic review strategy.The supplier's multiperiod decisions for the optimal inventory levels held in the retailer' s shelf space are myopic，thus the single-period optimal inventory level under VMI revenue-sharing contract can determine the optimal shelf space.

VMI；inventory competitive product；replenishment policy；optimal shelf space

F253.4

：A

1003-207（2014）04-0042-09

2011-03-28；

2013-03-16

广东省哲学社会科学“十一五”规划项目（GD10CGL14）

杨建功（1971-），男（汉族），河南三门峡人，广东金融学院副教授，研究方向：物流与供应链管理.