错误综合评价法的研究与应用

黄灏然，郭开仲，郑 琦

（1.仲恺农业工程学院，广东广州510225；2.广东工业大学，广东广州510520）

错误综合评价法的研究与应用

黄灏然1，郭开仲2，郑 琦1

（1.仲恺农业工程学院，广东广州510225；2.广东工业大学，广东广州510520）

针对同时包含定性指标、定量可线性补偿和定量不可线性补偿指标的综合评价问题，本文提出一种新型的消错决策方法。在错误、错误值、错误函数等消错学概念的基础上，提出了极限损失值、重要指标、关键指标、冗余指标等概念，给出不同形式的错误函数。通过错误值和极限错误损失值求取错误损失值，并以此为基础进行综合评价。污水处理厂建设方案评价的实际研究结果表明错误综合评价法能够有效的对定性指标进行量化、能够同时处理包含可线性补偿和不可线性补偿的定量指标。

错误综合评价；错误值；极限损失值；建设方案综合评价

1 引言

综合评价问题是指从全局和整体的角度对某一特定的对象系统进行排序或分类的问题［1-4］。对综合评价问题的研究涉及评价指标体系和综合评价方法［4］。评价指标体系中的指标可以分为定性指标和定量指标。定量指标又可以分为两类：一类是各项指标的得分值可以相互线性补偿；另一类是不可以相互线性补偿。对于后者，只要有一个指标不满足要求，其余指标无论得分值多高，对象系统都将被否决（即“一票否决制”）。传统的综合评价方法如加权平均法、层次分析法、模糊综合评判法、理想点法、因子分析法、灰色关联评价法等［5-8］，大多要求评价指标的类型为两类定量指标中的一种，且通常对难以量化的定性指标无能为力。当评价指标体系包含定性（难量化）、定量可线性补偿和定量不可线性补偿指标中的任意两类或两类以上时，传统方法难以进行评价或评价效果不佳。

本研究将针对上述问题，在错误、错误函数等消错学概念的基础上，提出了极限损失值、重要指标、关键指标、冗余指标等概念及定理，构建一种能够处理包含两类或两类以上指标的新的综合评价方法。

2 相关的概念与定义

消错学是由郭开仲教授创立的一门关于系统分析错误的原创性理论，其理论框架包含了错误的概念、判别错误的规则、错误集论、错误函数、错误系统理论、错误逻辑、应用理论等方面内容［9-16］。该学科自1986年创立以来受到科学院院士张钟俊教授等数十位国内外专家学者的好评，Xiong Haiou［13］、孙东川和刘世勇［16］、闵惜琳［15］等学者们分别对错误集、错误逻辑对实践的影响、错误矩阵等内容展开研究。目前研究体系不断完善、研究成果日趋丰富。根据研究的需要，本文在引用错误、错误函数等概念的基础上，提出极限损失值、重要指标等概念，推导出相关定理。

定义1 设U是论域、u∈U，G是U上的一组确定且有资格的规则，若从G推不出u（包括G完全、部分或不肯定推不出等），则称u在U上对于规则G是错误的。［14-17］

定义2 设U是论域，G是U上的一组规则，令V=｛（u，G）|u∈U｝，f：V→R，则称f为定义在U上对于规则G的错误函数，简称为U上的错误函数，记为x=f（G，u），简记为f（u），其中R为实数域、x为对象u在规则G的错误值［18］。

定义3在对象系统S中，对于某固有功能GYj（j=1，2，……n，下同），若把要素（或子系统，下同）zi（i=1，2，……，m）从系统中去掉，那么固有功能GYj只能实现原来的［0，t%］（0≤t≤100）范围［17］。当t=0时，zi对于系统S的固有功能GYj起着关键作用，称之为关键要素；当t=100时，zi对于系统S的固有功能GYj是多余的，称之为冗余要素；当0＜t＜100时，zi对于系统S的固有功能GYj是重要的，称之为重要要素。

在定义1和定义3的基础上，本文对极限损失值作如下界定。

定义4 在对象系统S中，对于某固有功能GYj，要素zi（i=1，2，……，m）完全错误时，固有功能GYj减少的数值称为zi对于GYj的全错损失值，又称极限损失值，表示为k，k=ΔGYj。

定理1 冗余要素的极限损失值k=0。

证明：根据定义3可知，对于冗余要素其自身正确与否并不影响某固有功能GYj的实现，即ΔGYj≡0，因此极限损失值k=0。证毕。

3 错误综合判别法的构建

3.1 评价指标体系的构建与指标分类

选取、构建科学合理的评价指标体系是进行科学有效的综合评价的前提。错误综合评价法对指标选取的要求与其他综合评价方法类似。

在前文消错学的相关概念和定义基础上，根据评价指标对固有功能的影响程度，可以将评价指标分为关键指标、重要指标和冗余指标三类，推导出两个反映这三类指标特性的定理。

定义5对于某固有功能GYj（j=1，2，……n），反映或衡量对象系统S中的关键要素、重要要素和冗余要素的指标分别称为关键指标、重要指标和冗余指标。

定理2 在综合评价过程中，冗余指标是多余的应该去除。

证明：根据定义3和定理1可知冗余要素对对象系统的某固有功能的实现是多余的，冗余要素的极限损失值为0，这就是说冗余指标的得分值大小不应对评价结果产生影响。因此，在综合评价的过程中冗余指标是多余的应该去除。证毕。

定理3 定量关键指标属于线性不可补偿指标，定量重要指标属于线性可补偿指标。

证明：根据定义3和定义5可知，当任何一个关键指标发生错误时，不管指标体系中的其他指标取值如何，对象系统的某固有功能GYj必将全部丧失，这就说明定量关键指标的得分值是不可以相互线性补偿的，即定量关键指标属于线性不可补偿指标。当任何一个重要指标发生错误时，对象系统的固有功能GYj只是部分丧失，其他重要指标的得分值的提高能够引起固有功能GYj的提升，这就说明定量重要指标属于线性可补偿指标。证毕。

对于定量型指标，还可以从取值要求的角度将其分为效益型、成本型、固定型和区间型。

综上所述，在综合评价过程中，定性指标可以分为定性重要指标和定性关键指标2种；定量指标可以从两个维度分为8种不同类型。因此，在评价的过程中，评价指标一共可以分为10种类型，如表1所示。

在构建出对象系统的评价指标体系后，需要进行系统分析和判断，指标体系中的各个指标属于上述10种类型中的哪一种。这将影响到错误函数的选择，错误值和极限损失值的计算。

3.2 各指标错误值的计算

错误函数f（u），根据值域ran（f）在实数R中的不同可以分为经典错误函数（ran（f）=｛0，1｝）、模糊函数（ran（f）=［0，1］）、具有临界点的错误函数（ran（f）=［-1，+1］）、非负错误函数（ran（f）=［0，+∞））［18］。根据消错理论，不同类型的指标根据其自身特点都可以采用一种或多种错误函数来计算错误值的大小。

为了使得各指标间的错误值具有可比性，各指标错误值必须拥有相同的数量级。经典错误函数、模糊错误函数、具有临界点错误函数的函数值的绝对值落在［0，1］之间，数量级相同，另外上述10类指标的错误值能够通过这三类错误函数中的一种或多种表示，因此本文选择这三类错误函数用于计算各个指标的错误值。

对于定性指标，适宜采用经典错误函数进行量化［17］。对于定量指标中的关键型指标，任何一点错误都会导致系统功能无法实现，该类指标要么没有发生错误没有带来损失、要么发生错误造成固有功能GYj的全部丧失，因此错误值也适宜采用经典错误函数的形式表示。经典错误函数的表达式相对简单，如式（1）所示。

其中U是论域、u∈U，G是U上的一组确定且有资格的规则。

对于定量指标中的重要指标其错误大小存在一定的模糊性，适宜采用模糊错误函数或具有临界点错误函数进行求取。不同类型的指标，应使用不同的错误函数来计算其错误值。设si为指标i的评价值，si≥0；a为的效益重要型指标的目标效益值，a≥0，当a没有明确取值要求时，可选择各个评价对象中的最大值；b为成本重要型指标i的目标成本值，b≥0，当b没有明确取值要求时，可选择各个评价对象中的最小值；c为固定重要型指标的目标值，c≥0；d=［d-，d+］为区间重要型指标的目标值，d-＜d+。那么对于不同指标类型可以建立如下相应的错误函数。

（1）效益重要型指标。该类型指标，要求si≥a，si越小于a错误越大，越大于a正确度越大，其错误值适宜采用具有临界点的错误函数f（u），如式（2）所示：

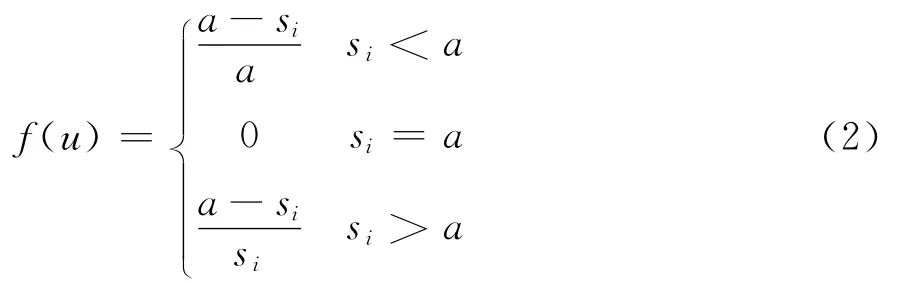
（2）成本重要型指标。该类型指标要求si≤b，si越大于b错误越大，越是小于b正确度越大，其错误值适宜采用具有临界点的错误函数f（u），如式（3）所示：

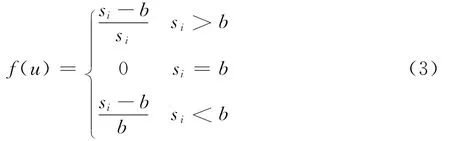
（3）固定重要型指标。该类型指标要求si=c，si越偏离c错误越大，其错误值适宜采用模糊错误函数表示，如式（4）所示：

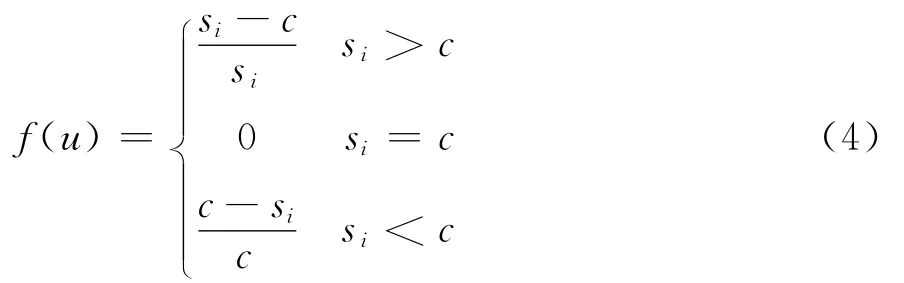
（4）区间重要型指标。该类型指标要求si∈［d-，d+］，si越偏离区间错误越大，其错误值适宜采用模糊错误函数表示，如式（5）所示：

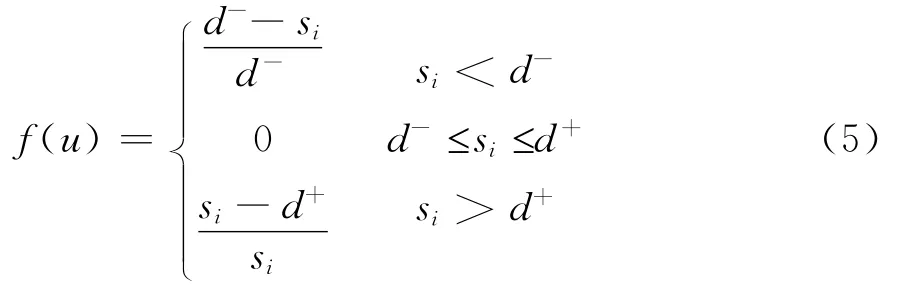
各类指标的错误值计算函数如表1所示。

3.3 各指标极限损失值的计算

根据定义3和定义5可知，当任何一个关键指标发生错误时，对象系统的某固有功能GYj必将全部丧失，这就说明关键指标的得分值是不可以相互线性补偿的，这种损失是巨大的。这时极限损失值可用一个无穷大的数字M表示（为计算方便，M取104就足够），M值不仅能够表示错误所造成的巨大损失，而且有利于在计算过程中解决关键指标不可线性补偿的问题。

对于重要指标，可假设指标体系中所有重要指标的总功能为100，然后通过利用FD法、多比例评分法、DERE法、逻辑判断评分法等求取各重要指标的功能值。某指标最后求取到的功能值便是该指标完全错误时的损失值，即极限损失值。各类指标的极限损失值如表1所示。

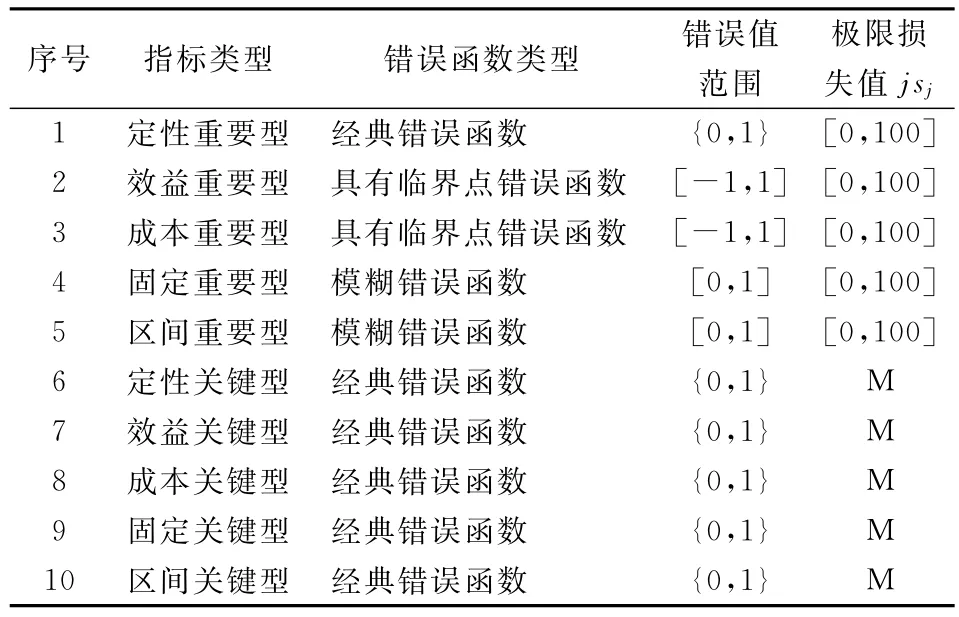
表1 指标的错误函数类型和极限损失值

3.4 错误综合评价

根据前文3.2和3.3可知，某一指标的错误损失值等于该指标的错误值和极限损失值的乘积，即：

其中，lj表示指标j的错误损失值，xj表示指标j的错误值，kj表示指标j的极限损失值，j=1，2，…，n。

对象系统i所有指标的错误损失值之和，便是该对象系统的综合错误损失值Li，即：

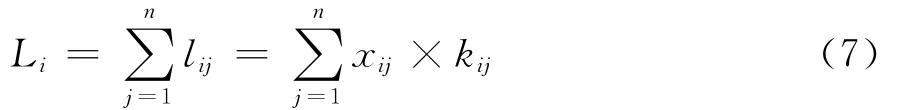
其中，i=1，2，…，m。

将各对象系统的综合错误损失值按由小到大顺序排列，排序结果即是最终综合评价结果。

4 应用实例

应用错误综合评价法对污水处理厂进行综合评价。相关数据来源于笔者的实地调研、文献资料查阅和前期研究成果［17］的基础上得到。

4.1 数据资料简述

广州市某污水处理厂按照政府规划，拟进行二期工程建设，可用面积为2.1公顷，要求建成后日污水处理能力在20-25万吨，服务范围最好能覆盖周边48.6平方公里面积。参照GB18918-2002一级标准和DB44/26-2001一级标准中的较严指标，污水处理厂必须在技术上保证排放水质的合格率在98%以上。污水处理厂的运营效率希望能够达到或超过国内主流污水处理系统（UNITANK系统）的效率。UNITANK系统的相关参数为：土地利用0.25m2/m3污水、耗电0.215kwh/m3污水、单位运营成本0.49元/m3污水、单位处理成本0.73元/ m3污水、投资效率883.77元/m3污水［17］。污水处理过程产生的臭气必须经过处理后才能排放，处理率尽量争取达到95%以上。另外，结合年度财政预算、拨款和社会需求等影响因素，要求项目工期必须控制在18-24个月之间。现有A、B、C、D四套建设方案，具体情况如表2所示。

4.2 污水处理厂建设方案的综合评价

根据上述资料，经过分析可得污水处理厂建设方案的评价指标和指标类型如表2所示。显然在该综合评价问题中，同时涉及了定性指标（如指标1）、定量可线性补偿指标（如指标2）和定量不可线性补偿指标（如指标6）三类指标，利用传统的方法难以进行综合评价，而采用本文设计的错误综合评价法则能够效解决该问题。利用公式（1）-（5）计算错误值，利用DARE法［19］求各重要指标的极限损失值，结果如表3所示。根据公式（7）计算出四个方案的总错误损失值分别为：LA=11.34、LB=19.66、LC= M、LD=4.67。总错误损失值排序结果为LD＜LA＜LB＜LC，即最佳的方案为D方案。

5 结语

本文利用消错学理论构建出错误综合评价法，并通过具体实例来验证该方法的可行性。结果表明错误综合评价法能够有效的对定性指标进行量化，而且能够同时处理包含定量可线性补偿和定量不可线性补偿的指标。与传统的综合评价方法相比，错误综合评价法的优势在于能够处理同时包含三类指标的综合评价问题。

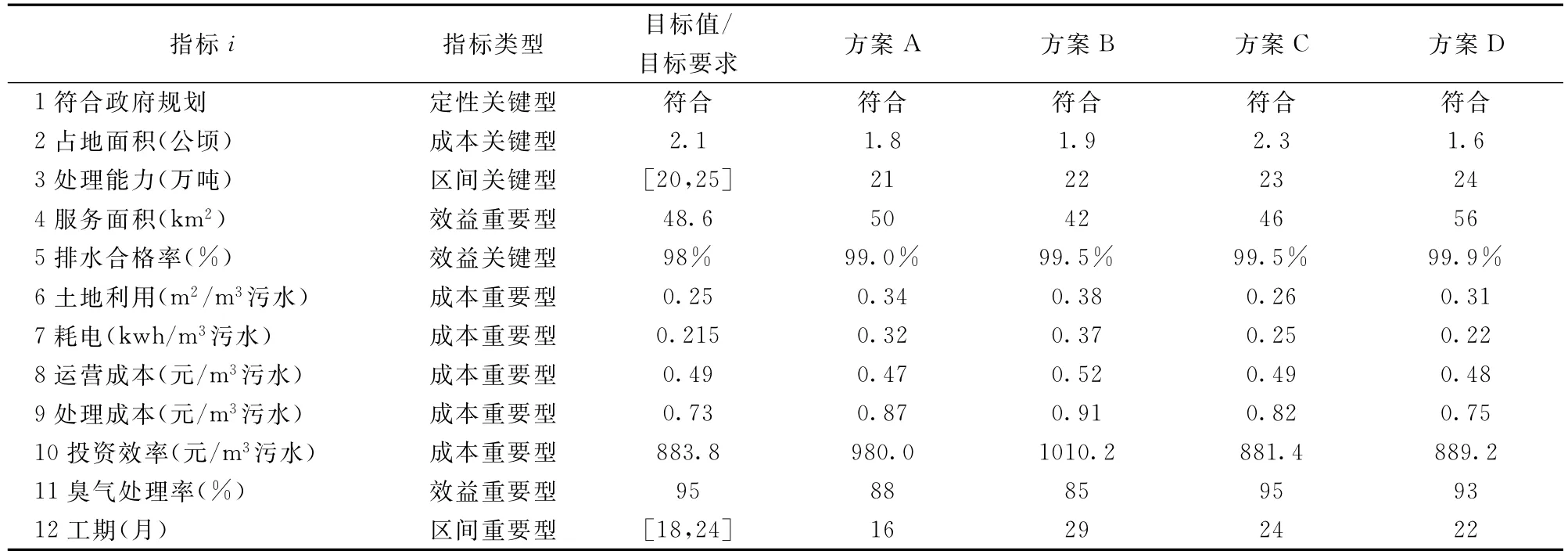
表2 污水处理厂的评价指标及相关指标值

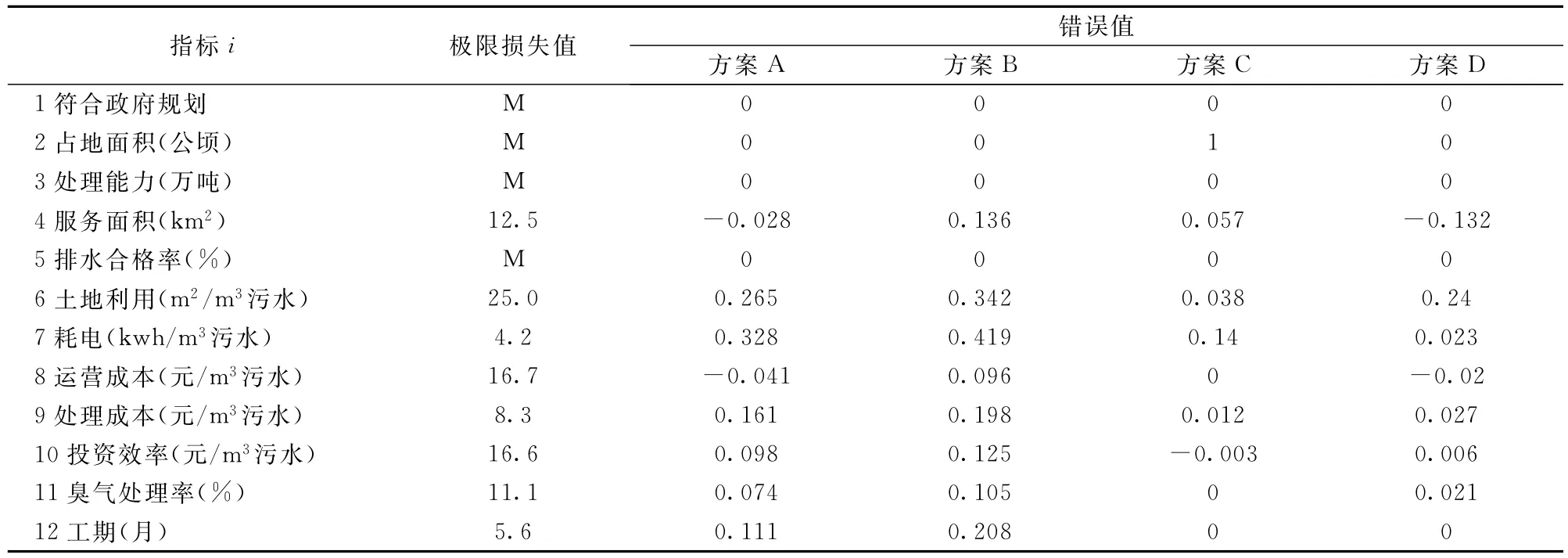
表3 极限损失值和错误值的计算

参考文献：

［1］Xu Jianling，Tang Zhanhui，Shang Jincheng，et al. Comprehensive evaluation of municipal garbage disposal in Changchun City by the strategic environmental assessment［J］.Environmental Science and Pollution Research，2010，7（5）：1090-1097.

［2］Che Shengquan，Wang Yun，Gong Bin.Comprehensive evaluation method of urban remnant natural area：A case study of Shanghai，China［J］.Journal of Shanghai Jiaotong University（Science），2008，13（5）：589-594.

［3］郭亚军.一种新的动态综合评价方法［J］.管理科学学报，2002，5（2）：49-54.

［4］陈衍泰，陈国宏，李美娟.综合评价方法分类及研究进展［J］.管理科学学报，2004，7（2）：69-79.

［5］Dong Yucheng，Zhang Guiqing，Hong Weichiang，et al. Consensus models for AHP group decision making under row geometric mean prioritization method［J］.Decision Support Systems，2010，49（3）：281-289.

［6］Ju Yanbing，Wang Aihua.Emergency alternative evaluation under group decision makers：A method of incorporating DS/AHP with extended TOPSIS［J］.Expert Systems with Applications，2012，39（1）：1315-1323.

［7］Gong Li，Jin Chunling.Fuzzy comprehensive evaluation for carrying capacity of regional water resources［J］. Water Resources Management，2009，23（12）：2505-2513.

［8］Rodrigues P C，Lima A T.Analysis of an European union election using principal component analysis［J］. Statistical Papers，2009，50（4）：895-904.

［9］Min Xilin，Guo Kaizhong.Knowledge model based on error logic for intelligent system［C］.Proceedings of World Congress on Computer Science and Information Engineering Los Alamitos，CA，March31-April2，2009.

［10］Min Xilin，Guo Kaizhong.A knowledge discovery method based on error matrix equation［C］.Proceedings of Sixth International Conference on Fuzzy Systems and Knowledge Discovery，Tianjing，August 14 -16，2009.

［11］Min Xilin，Guo Kaizhong.A primary probe on the application of error eliminating theory in urban traffic jam management system［J］.Advances in System s Science and Applications，2009，9（3）：486-493.

［12］Huang Jize，Xiong Haiou，Guo Kaizhong.Research on systematic mechanism of＂one percent of a thing can result in a hundred-percent error＂［C］.Proceedings of IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Wuhan，December 21-22，2008.

［13］Xiong Haiou，Huang Jize，Guo Kaizhong.The transformation of fuzzy error set in a system intelligent decision making［C］.Proceedings of International Conference on Advanced Computer Control，Singapore，January 22-24，2009.

［14］Min Xilin，Guo Kaizhong.Research on the application of fuzzy error logical in system optimization［C］.Proceedings of IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Wuhan，December 21-22，2008.

［15］闵惜琳.错误矩阵方程［M］.北京：科学出版社，2012.

［16］刘世勇，郭开仲，孙东川.管理科学中的一个创新性研究——错误理论的提出、进展和展望［J］.管理学报，2010，7（12）：1749-1758.

［17］郭开仲.错误系统［M］.北京：科学出版社，2012.

［18］郭开仲，张式强.错误集论［M］.长沙：中南大学出版社，2001.

［19］孙东川，林福永，孙凯.系统工程引论（第2版）［M］.北京：清华大学出版社，2009.

Research and Application of Error Comprehensive Evaluation Method

HUANG Hao-ran1，GUO Kai-zhong2，ZHENG Qi1
（1.Zhongkai University of Agriculture and Engineering，Guangzhou 510225，China；2.Guangdong University of Technology，Guangzhou 510520，China）

For comprehensive evaluation problem including qualitative index，linear and nonlinear compensation index，a new error comprehensive evaluation method is proposed.Based on the concepts of Error，error-function and error-value，the maximum loss value，important index，key index，redundant index and various types of error-function are given.The error-loss-value could be calculated by using the Error-value and maximum loss value，which is the basis of comprehensive evaluation.Furthermore，The construction of the wastewater treatment plant is chosen for evaluation.The result shows that error comprehensive evaluation can quantify the qualitative index effectively and also be good at deal with the linear and nonlinear compensation evaluated problem.

error comprehensive evaluation；error value；maximum loss value；comprehensive evaluation of construction scheme

N945.16；C934

：A

1003-207（2014）04-0119-05

2012-04-09；

2013-03-22

国家社会科学基金资助项目（09BTQ008）；国家科学技术学术著作出版基金（201086）

黄灏然（1982-），男（汉族），广东汕头人，仲恺农业工程学院，在读博士，讲师，研究方向：管理系统工程、消错理论.