搭接网络中的路长悖论及其特性研究

阚芝南，孔 峰，乞建勋

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学经济与管理学院，河北保定 071003）

搭接网络中的路长悖论及其特性研究

阚芝南1，孔 峰2，乞建勋1

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学经济与管理学院，河北保定 071003）

本文发现在搭接网络中存在“工序间加入不同表现形式的同一时间约束，可能会产生不同的最大路长”这个悖论。通过研究此悖论形成原因从而提出搭接网络的一种新表示方法。该方法不但与经典的CPM网络在表示形式上完全统一，而且在求解时间参数及关键路线的方法上也保持一致。该新表示法使得CPM网络中许多基础理论可以推广到搭接网络中来，例如工序的总时差Tij等于关键路长与过该工序（ij）的最大路长之差（-）；任意一条路线μ上自由时差的和都等于关键路长与该条路的路长之差（-μ-）等。利用这些定理与规律，本文解决了搭接网络中如何正确求解时间参数问题，提出在搭接网络中评估关键路长与次关键路长之差的简便方法以及求解搭接网络次关键路线的一系列精确算法，并通过算例表明这些方法在搭接网络应用中的具有有效性与简便性。

搭接网络；最大路长；机动时间；CPM网络

1 引言

搭接网络是在经典的CPM网络基础上的发展。在CPM网络中，主要表达的是工序间严格的“结束-开始”型（F-S型）的时间约束，在搭接网络中，工序间不仅有“结束-开始”型（F-S型）的时间约束，还有“结束-结束”（F-F）、“开始-开始”（S-S）、“开始-结束”（S-F）型的时间约束。用一句话来概括，CPM网络表示的是不含交叉作业的计划而搭接网络表示的是带有交叉作业的计划，因而搭接网络比经典的CPM网络适用面更广，更接近于工程的实际。

Crandall［1］在1973年提出搭接网络后广泛吸引了各国学者的注意。Bartusch［2］等人在1988年提出，可以对单代号的搭接网络进行标准化转换，即将各种不同的时间约束均转化为一种时间约束，例如S-S型时间约束，并给出了转化的方法。Elmaghraby［3］在1992年提出了搭接网络的双代号模型，并用数学规划的方法求解该网络中的时间费用权衡问题。1998年以来，在带有搭接关系的网络中求解实际的问题成为了研究的热点。De Reyck等人［4-5］分别提出了解决搭接网络中的资源约束下的项目调度问题的分支定界法和解决搭接网络中带有现金流和资源约束的项目调度问题的一种优化方法；接着又在1999年时提出了搭接网络中多资源约束下的项目调度问题［6］。解决带有搭接关系的资源约束下的项目调度问题的不同启发式算法综述可以参看Brucker［7］。而De Reyck［8］，Schwindt［9］，以及Fest［10］讨论了该问题的精确算法。Dorndorf［11］提出了一种新型的分支定界法来解决带有搭接关系的资源约束下的项目调度问题。Sakellaropoulos［12］、Chassiakos［13］分析了搭接网络中的时间-费用权衡问题。Najafi［14］提出了一种遗传算法解决带有现金流的搭接网络中的资源约束下的项目调度问题。Bianco等［15-17］不断的在寻找求解一般优先关系网络中的资源约束下的项目调度问题的最短总工期的精确算法。

我国对于搭接网络的研究比较晚，目前普遍认可的搭接网络模型主要通过引入“等效时距”的概念来建立单代号网络模型。由于引入了“等效时距”的概念，该搭接网络模型不论在计算工序的时间参数、工序的机动时间还是网络总工期上，甚至在关键路线的确定上，与发展成熟的CPM方法相比都麻烦了不少。因此我国目前对搭接网络的研究主要集中于对搭接网络的模型建立方法［18-19］、搭接网络中时间参数和机动时间的计算方法、关键链的确定［20］、以及如何用双代号网络表示搭接网络这些基础问题的研究。由于双代号网络的广泛应用，一些学者还致力于将建立的单代号搭接网络计划转化为双代号网络计划［21-23］。我国学者在这方面的论文主要有闫瑾、张奉举［24］的“单代号搭接网络模糊工期的计算方法”；杨冰［25］的“网络计划计算模型的统一”，魏道升、张智洪［26］的 “搭接网络计划在公路和桥梁施工项目管理中的应用”；李金云［27］的“搭接网络计划时间参数计算方法的改进”；黄彬、孟国勇［28］的“工程搭接网络浅议”；张昭煌、梁会森［29］的“搭接网络计划工作总时差计算方法”等。

本文发现当在CPM网络中增加不同表达类型的同一搭接关系时，会造成网络最大路长不一致的奇异现象。在对该奇异现象进行研究中，发现CPM网络只能表达F-S型时间约束，而不能表达F-F，SS，S-F型时间约束，因此在运用CPM网络技术建立搭接网络模型时，只有将所有类型的搭接关系均转化为“结束-开始”型（F-S）时间约束才能正确表达工序与工序间的搭接关系，本文进一步对这一结论的正确性做出详细的论述与证明。这种新的搭接网络模型实现了CPM网络与搭接网络表示的统一，因此搭接网络中工序时间参数的计算方法、机动时间大小的计算，与CPM完全统一，二者使用的计算公式一样，求得的值完全一样，由此解决了总工期和关键路径的唯一确定问题以及时间参数简单计算问题等目前搭接网络研究的热点问题；本文在此基础上进一步对搭接网络的机动时间特性进行了深入的研究，发现了在搭接网络中工序的总时差Tij等于关键路长与过该工序（ij）的最大路长之差（-）；任意一条路线μ上自由时差的和都等于关键路长μ-与该条路的路长之差（-μ-）等结论。并利用这些推导出的结论设计了评估关键路长与次关键路长之差的简单方法以及寻找网络次关键路线的一系列精确算法，使搭接网络中的管理风险进一步降低并为以后深入的解决搭接网络中的各种应用问题打下了坚实的基础。

2 搭接网络中的时间约束类型及表示方法

最早开始 节点（i）的最早开始ESi是指从节点（i）开始的各项工序最早可能开始工作的时刻。节点（i）的最早开始ESi等于节点（i）的紧前工序最早结束的最大值，用公式表示为ESi=max｛EShi+Thi｝。

工序（ij）的最早开始ESij是指紧前工序完成之后，工序（ij）可能开始的最早时间。工序（ij）的最早开始ESij等于节点（i）的最早开始，用公式表示为ESij=ESi。

最迟结束 节点（j）的最迟结束LFj是指以该节点（j）为结束的各项工序最迟必须完成的时刻。节点（j）的最迟结束LFj等于节点（j）的紧后工序最迟开始的最小值，用公式表示为：

LFj=min｛LFjk-Tjk｝

工序（ij）的最迟结束LFij是指指工序（ij）最迟必须结束的时间。工序（ij）的最迟结束LFij等于节点（j）的最迟结束，用公式表示为LFij=LFj

最迟开始 工序（ij）的最迟开始LSij是指工序（ij）最迟必须开始的时间。其大小为：

LSij=LFi-Tij

最早结束 工序（ij）的最早结束EFij是指工序最早可能完成的时间。工序 （ij）的最早结束EFij就是它的最早开始时间加上该工序的工期，用公式表示为EFij=ESi+Tij。

总时差 工序（ij）的总时差TFij表示在不影响项目总工期的条件下，各工序的最早开始（结束）时间可以推迟的最大时间间隔。工序（ij）的总时差TFij等于TFij=LFj-ESi-Tij。

自由时差 工序的自由时差是指工序在不影响其紧后工序最早开始前提下，该工序结束时间最多可延长的时间。工序（ij）的自由时差FFij等于工序（ij）的最早结束时间与其紧后工序的最早开始时间之差，用公式表示为：

FFij=ESjk-EFij=ESj-ESi-Tij

安全时差 工序的安全时差是指工序的紧前工序在最迟结束时间结束时，该工序不影响总工期时最多可以延迟的时间。工序（ij）的安全时差SFij等于工序（ij）的最迟开始与其紧前工序最迟结束时间的差，用公式表示为：

SFij=LSij-LFhi=LFj-LFi-Tij

在搭接网络中搭接关系，主要是通过工序之间各种时间约束来体现的。工序间的搭接关系主要有以下几种：

（1）结束-开始型约束（F-S）表示工序A结束后至少r天工序B才能够开始，记为

（2）结束-结束型约束（F-F）表示工序A结束后至少r天工序B才能够结束，记为

（3）开始-开始型约束（S-S）表示工序A开始后至少r天工序B才能够开始，记为

（4）开始-结束型约束（S-F）表示工序A开始后至少r天工序B才能够结束，记为

3 搭接网络中的“路长悖论”

我们在研究搭接网络的过程中发现了一个关于路长的悖论：在网络中加入同一约束的不同表达形式，分别计算出的网络最大路长不相等。例如，图1是个普通双代号CPM网络计划图。

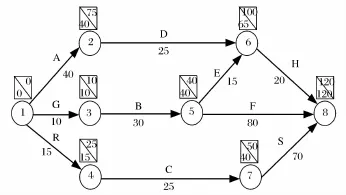
图1 普通双代号CPM网络计划

图2 增加时间约束“FAFB”、“SBSC”后的网络图

图中，时间约束我们用点划线“○-····-→○”表示，我们把这类箭线称约束工序，时间约束工序的特点是只消耗时间但不消耗资源；实工序用一条实箭线表示“○→○”，实工序既消耗时间又消耗资源；虚工序用虚箭线表示“○-→○”，虚工序既不消耗时间又不消耗资源，它只代表一种逻辑顺序关系：虚工序的紧前工序全部结束后，虚工序的紧后工序才能开始。虚工序看做“r=0”的约束工序。由图2可知，加入时间约束“FA→—65FB”，“SB→—20SC”之后网络的最大路长为140天。现在对增加的约束换成另外一种等价类型，将原先的F-F型约束和SS型约束均替换为等价的F-S型约束，如图3所示，却与上面图2中的最大路长不一致。

图3 转化为“FASB”，“FBSC”后的网络图

因为“A结束后至少65天，B工序才能结束”等价于“A工序结束后至少（65-30）=35天，B才能开始”；而“B开始后至少20天，C才能开始”等价于“B结束后至少（20+30）=50天，C工序才能开始”。因此将“”替换为“”，“SB”替换为“”是一种等价变换，图2与图3的总工期也应当相等。

但是由图3可知，网络的总工期由140天变为250天。为什么同一个约束条件却得到完全不等的总工期呢？

4 “路长悖论”的分析

在经典的CPM网络中工序最早计算公式为

ESij=max｛EFk1i，EFk2i，…，EFkni｝

代表工序（ij）必须在所有的紧前工序（k1i），（k2i），…，（kni）全部结束后，该工序（ij）才能开始，因此，这种时间约束是“结束-开始”型的时间约束。

因此，在一条路线μ上的工序，前边的先开始，后面的后开始，例如图4所示：

图4 路线μ示意图

在路线μ上的工序（ab）在前，则（ab）先开始，（ab）结束后，（bi）才能开始，（bi）结束后，（ij）才能开始。所以在一条路线上的工序彼此间都有时间约束。在图4，可以认为“（ij）工序结束后至少50天，（kr）工序才能开始”，因此这是典型的“结束-开始”型约束：“”。所以CPM网络是可以表达“结束-开始”型的时间约束的。

在CPM网络中，不在同一条路线上的工序称为平行工序，平行工序之间没有任何时间约束。例如在图一中，D工序和E工序不在同一条路线上，它们是平行工序，则D和E之间没有任何时间约束，既不能表示“D结束后E才能结束”又不能表示“E结束后D才能结束”，D和E之间谁先谁后，没有任何约束。同理，因为图2中A与B是平行工序，二者不存在任何约束，因此不能满足“A结束65天B才能结束”这一约束，所以图2的表示方法不对。相反，在图3中A与B在同一条路线上，它们之间存在时间约束，表示“A结束后至少35天B才能开始”，因此图3中的表示方法才是正确的。

所以搭接网络中所有的“结束-结束”型的时间约束，都需要等价变成“结束-开始”型的时间约束，这样在CPM网络中才能正确表达出来。

同理在图1中，E、F两工序不在同一条路线上，因此二者之间不存在任何时间约束，既不表示“E开始后F才能开始”，也不表示“F开始后E才能开始”。因此，在图2中，B和C不在同一条路线上，所以B和C之间不存在任何约束，因此，图2无法表达“B开始后至少20天C才能开始”这种时间约束。而在图3中，等价转化成“结束-开始”型约束后的B与C变成了一条路线上的工序，能够表示“B结束后50天，C才能开始”，所以图3的表示方法才是正确的。

因此搭接网络中的“开始-开始”型约束，都需要先等价转化为“结束-开始”型的时间约束，才能用CPM网络表达这些约束。

同理“开始-结束”型的时间约束也必须转化为“结束-开始”型时间约束，才能用CPM网络表示。因为CPM网络只能表达“结束-开始”型时间约束。

用这种等价转化的方法表达各种时间约束，既简单，又能与CPM相统一，但是目前人们都没有采用这个方法，而是另起炉灶，独立设计了各种表示方法。这些表示方法虽然多种多样，但是一个共同点是不能与CPM统一，而在实际应用中人们已经习惯运用CPM的表达方法，换上一种新的表示方法，不仅复杂，还大大影响了它的实用功能。而利用等价转化的方法就可以克服以上的缺点，十分利于网络计划的推广。

下面给出在搭接网络中各种约束关系等价转化为“结束-开始”型时间约束“”的具体公式及证明，供参考：

证明：“结束-结束”型最小约束FA→—rFB，表示工序A结束后至少r天，工序B才能结束，即：

因为FB=SB+TB，所以：

FB-FA=（SB+TB）-FA≥r

得SB-FA≥r-TB

再由（3）式，

式（2）成立。证毕。

式（4）成立。证毕。

证明：“开始-结束”型最小时间约束，记为“SA”，表示工序A开始后至少r天，工序B才能结束，即SB-FA≥r

式（5）成立。证毕。

把各种时间的约束都转化为“结束-开始”型时间约束后，画出的CPM网络图，成为等价的CPM网络图，记为G*。

5 在等价CPM网络G*中，机动时间与路长的联系规律

在G*中，实工序、约束工序、虚工序在计算路长和各种事件参数时，都视同为实工序，与在经典的CPM网络G中，计算各种时间参数时都把虚工序视同为零的实工序一样。

（1）任意节点（i）与源点（1）之间的任意路线μ1-i上自由时差与路长的联系规律。

在路μ1-i上各工序的自由时差的和等于节点（i）的最早开始ESi与该路长μ-1-i的差（ESiμ-1-i），即：

证明：设μ（1，i）=（1）→（a）→（b）→（c）→…→（f）→（g）→（h）→（i）则：

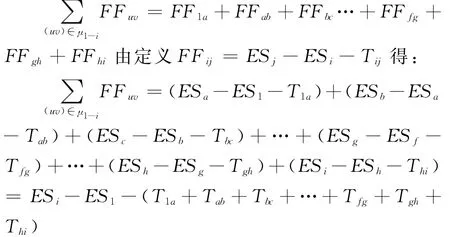
因（1）是源点，所以ES1=0，又因：

所以：

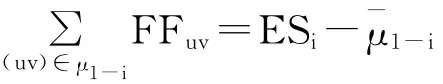
证毕。

此时的μ1-i称为节点（i）的前主链μ*i。

证明：在式（6）中令μ1-i=μ*i得：

已知

因（w）为汇点，所以ESw=。-证毕。

（2）任意节点（i）与汇点（w）之间的任意路线μi-w上安全时差与路长的关联规律路线μj-w上各工序的安全时差的和等于汇点（w）的结束时间LFw与该节点（i）的结束时间LFi之差（LFw-LFi）再减去该路长，即：

证明：设任意节点（i）与汇点（w）之间的任意路线段为：

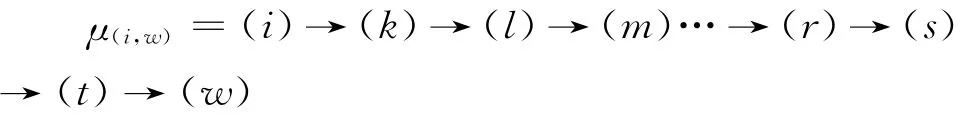
则：

再由定义SFij=LFj-LFi-Tij可得：

因为：

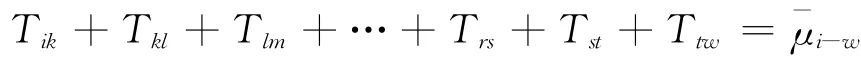
此时的μi-w即为节点（i）的后主链。

因μ=μ1-w，则-，当i=1时，。（w）为汇点，所以LFw=。又因（1）为源点，则LF1= 0，证毕。

（3）总时差和路长的关系

任意工序的总时差TFij都等于关键路长μ-∇与过该工序的最大路长的差（-），即：

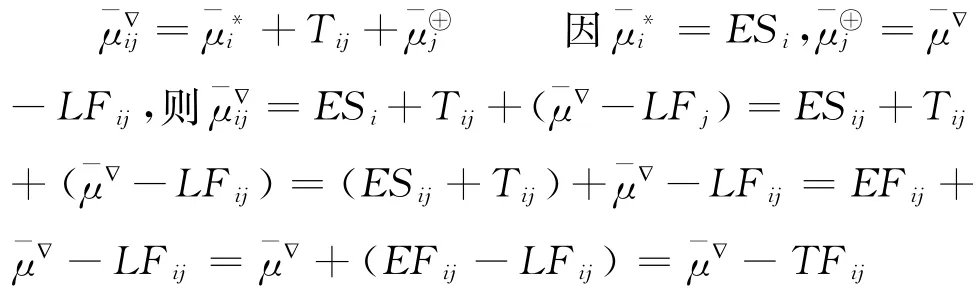
推论5：若TFij=0，则（ij）∈μ∇；若TFij＞0，则（ij）∉μ∇。

证明：当TFij=0，由式（12）0，则。

当TFij＞0，由式（12），＞0，

（4）节点时差与路长的关系

任意节点（i）的节点时差TFi都等于关键路长与过该节点（i）的最大路长之差（-）。即：

（5）自由时差与路长的关系

任意工序（ij）的自由时差FFij等于过结束节点（j）的最大路长减去过该工序（ij）的最大路长，即：

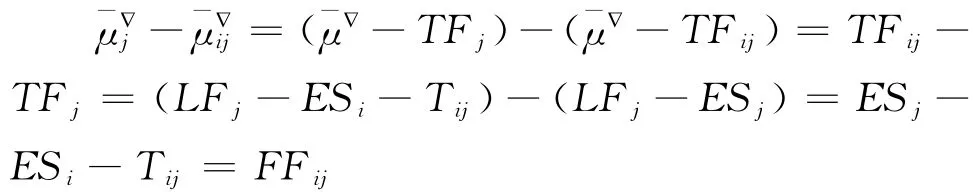
（6）安全时差与路长的关系

任意工序（ij）的安全时差SFij等于过开始节点（i）的最大路长减去过该工序（ij）的最大路长减去过该工序（ij）的最大路长，即：

6 机动时间与路长的联系规律的应用——搭接网络次关键路线的求法

在实际的项目进度计划管理和决策活动中，我们不但需要知道关键路线，控制关键工序，有时还需要知道网络中次关键路线，因为在次关键路线的长与关键路线的长度差异很小时，次关键路线往往很容易变成关键路线。因此在二者路长之差很小时寻找网络的次关键路线，控制好次关键路线上的工序也是十分重要的。目前搭接网络虽应用面十分广泛，但对于其研究仅仅局限于搭接网络中时间参数的确定、寻找关键路径、关键工序等这类基础特性的研究，还未见到如何寻找次关键路径与关键路径路长之差的评估，也没见到求次关键路线的简单算法。本文根据以上推导出的机动时间与路长的联系规律解决了这一问题，弥补了这一研究的空白，减少了推迟总工期的风险。

（1）自由时差法

①找出关键节点的紧前非关键工序中，自由时差的最小值FFij，FFij即为网络关键路线μ∇与次关键路线μ［1］的路长之差（μ∇-μ［1］）。

②判断（μ∇-μ［1］）的大小，若较小需要找出次关键路线μ［1］则到③，若较大则结束。

③找出工序（ij）开始节点（i）的前主链μi*以及结束节点（j）到汇点（w）的关键路线段。

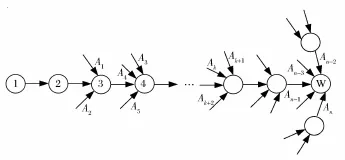
图5 关键路线示意图

图5中，1-2-3-…-W为网络的关键路线，A1，A2，A3，…，An-1，An为所有关键节点的紧前非关键工序，则所有的非关键路线μ≠μ∇必会经过A1，A2，A3，…，An-1，An中的一个工序。

如果经过多个Ai，按最后的Ai计算，则经过Ai的所有非关键路线μAi的集合设为｛μAi｝，i=1，2，…，n。那么网络中所有的非关键路线的集合为｛μ/μ

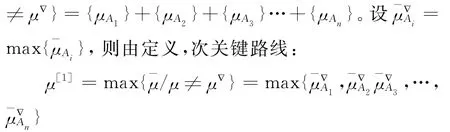
设Ai=（uv），由公式（7）μ-*u≥μ-1-u，公式（10）μ-⊕v≥μ-v-w，有：

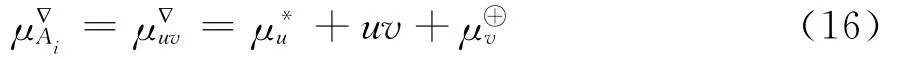
又因已知条件（v）∈μ∇，所以

网络次关键路线与关键路线的差值即为找出的紧前非关键工序的自由时差值。

设min｛FFA1，FFA2，…，FFAn｝=FFAk=FFuv，则由（6）：。

（2）安全时差法

①找出关键节点的紧后非关键工序中，自由时差的最小值SFij，SFij即为网络关键路线μ∇与次关键路线μ［1］的路长之差（μ∇-μ［1］）。

②判断（μ∇-μ［1］）大小，若较小需要找出次关键路线μ［1］则到③，若较大则结束。

③找出工序（ij）开始节点（i）到源点（1）的关键路线段以及结束节点（j）的后主链。

证明：与自由时差法类似，略。

（3）总时差法

①找出关键节点的紧前或紧后非关键工序中，总时差的最小值T，T即为网络关键路线与次关键路线的路长之差。

证明：与自由时差法类似，略。

7 案例

本文以杨冰在《网络计划计算的统一》［25］这篇论文中给出的一搭接网络计划为例，说明了转化为CPM形式后的网络与原网络求得的各类时间参数一致，运用CPM求解关键路线的方法就可以简便的找出该网络的关键路线，并利用推导出的机动时间与路长的联系规律判断出网络关键路线与次关键路线的路长之差，并找出网络的次关键路线。

该实例包含有F-F，S-F，S-S，F-S这几种基本搭接类型，表1给出了搭接网络计划的工序间的优先关系及工序工期。

对案例中的约束类型进行处理，将F-F，SF，S-S这三种类型的时间约束等效转化为F-S型的时间约束，得表2。根据表2的各工序间的优先关系、约束关系及工序工期，绘制CPM网络计划图，并计算时间参数得图6。得出的CPM网络计划图中的各工序的时间参数与原算例的单代号网络图的时间参数均一致，说明了转化方法是正确的。

表1 工序间的优先关系及工序工期

（1）以工序D为例，验证机动时间的总时差理论。

工序D的总时差TFD=13-2-6=5，过工序的最长路线为工序A-B-D-F，该路线的路长为10-7+8-9+6+14=22，关键路线的长度为27，可以发现，工序D的总时差=关键路线的路长减去过工序D的最大路长，即TFD=-，由此验证了总时差定理的正确性。同理可以验证其它的机动时间与路长的关联规律。

表2 将所有约束关系转化为F¯S型约束后的工序优先关系及工期

（2）以总时差法找出网络的次关键路线。

①找出关键节点的紧前或紧后工序中，总时差最小的工序为工序（2，3）总时差为5。可以得知网络的次关键路线与关键路线的路长之差为5。

②工序（2，3）的前主链为1-2，工序（2，3）的后主链为3-5-8-10-12-14。

所以次关键路线μ［1］=（1）→（2）→（3）→（5）→（8）→（10）→（12）→（14）

图6 计算实例的CPM网络计划图

8 结语

本文发现在CPM网络中加入搭接关系时，两工序间加入不同类型的同一时间约束，求出的网络最大路长会不一致这一悖论现象。通过对CPM网络中工序间的优先关系进行分析，发现运用CPM网络计划表示工序间的搭接关系时，只有将所有的时间约束均转化为结束-开始型（F-S）的时间约束，才能在CPM网络中正确表达工序间的搭接关系，并对这种转化进行了正确性分析与证明。这种转化方法使得运用CPM网络计划技术建立搭接网络模型变得可行。而目前搭接网络的研

究中，普遍认可的建模方法是将各种搭接关系转化为“等效时距”，再用单代号的网络计划形式表现出来。对于搭接网络中工序的时间参数、机动时间、网络总工期以及关键路径的确定都比较复杂。

本文运用CPM网络计划技术建立起的搭接网络模型不仅简单方便，还能把已发展成熟的CPM网络计划技术中的成果推广到搭接网络中来，有效的解决了目前搭接网络研究中的基本问题。本文在此基础上证明了“任意工序（ij）的自由时差FFij等于过结束节点 （j）的最大路长减去过该工序（ij）的最大路长”等一系列搭接网络中工序机动时间与路长的联系规律。利用这些规律设计了评估关键路长与次关键路长之差的简单方法以及寻找网络次关键路线的一系列精确算法，降低了搭接网络中的管理风险，并为以后深入的解决搭接网络中的各种应用问题打下了坚实的基础。

［1］Crandall K C.1973.Project planning with precedence lead/lag factors［J］.Project Management Quarterly，1973，4：18-27.

［2］Bartusch M，Mohring R H，Radermacher F J.Scheduling project networks with resource constraints and time windows［J］.Annals of Operations Research，1988，16（1）：201-240.

［3］Elmaghraby S E，Kamburowski J.The analysis of activity networks under generalized precedence relations（GPRs）［J］.Management Science，1992，38（9）：1245 -1263.

［4］De Reyck B，Herroelen W.A branch-and-bound algorithm for the resource-constrained project scheduling problem with generalized precedence relations［J］.European Journal of Operational Research，1998，111（1）：152 -174.

［5］De Reyck B，Herroelen W.An optimal procedure for the resource-constrained project scheduling problem with discounted cash-flows and generalized precedence relations.［J］Computers and Operations Research， 1998，25（1）：1-17.

［6］De Reyck B，Demeulemeester E，Herroelen W.Algorithms for scheduling projects with generalised precedence relations［M］//WOeglarz J.Project Scheduling-Recent Models，Algorithms and Applications.Boston，MA：Kluwer Academic Publishers，77-105.

［7］Brucker P，Drexl A，MNohring R，et al.Resource-constrained project scheduling：Notation，classification，models，and methods［J］.European Journal of Operational Research，1999，112（1）：3-41.

［8］De Reyck B.Willy Herroelen.The multi-mode resource-constrained project scheduling problem with generalized precedence relations［J］.European Journal of Operational Research，1999，119（2）：538-556.

［9］Schwindt C.A branch-and-bound algorithm for the resource-constrained project duration problem subject to temporal constraints［R］.Technical report，1998.

［10］Fest A R H，MNohring F，Uetz S M.Resource constrained project scheduling with time windows：A branching scheme based on dynamic release dates［R］. Technical report，1999.

［11］Dorndorf U，Pesch E，Phan-Huy T.A time-oriented branch-and-bound algorithm for resource-constrained project scheduling with generalised precedence constraints［J］.Management Science，2000，46（10）：1365 -1384.

［12］Sakellaropoulos S，Chassiakos A P.Project time-cost analysis under generalized precedence relations［J］.Advances in Engineering Software，2004，35：715-724.

［13］Chassiakos A P，Sakellaropoulos S P.Time-cost optimization of construction projects with generalized activity constraints［J］.Journal of Construction Engineering and Management，2005，131（10）：1115-1124.

［14］Najafi A A，Niaki S T A，Shahsavar M.A parametertuned genetic algorithm for the resource investment problem with discounted cash flows and generalized precedence relations［J］.Computers&Operations Research，2009，36（11）：2994-3001.

［15］Bianco L，Caramia M.A new formulation of the resource-unconstrained project scheduling problem with generalized precedence relations to minimize the completion time［J］.Networks，2010，56：263-271.

［16］Bianco L，Caramia M，A new lower bound for the resource-constrained project scheduling problem with generalized precedence relations［J］.Computers&Operations Research，2011，38（1）：14-20.

［17］Bianco L，Caramia M.An exact algorithm to minimize the makespan in project scheduling with scarce re-sources and generalized precedence relations［J］.European Journal of Operational Research，2012，219：73-85.

［18］杨冰.搭接网络计划计算模型的改进［J］.中国公路学报，2002，15（1）：116-122.

［19］杨冰.搭接网络计划模型分析［J］.北方交通大学学报，2002，26（5）：84-87.

［20］廖钰.搭接网络中关键链的识别方法［D］.武汉：华中科技大学，2007.

［21］夏中煌.实用双代号搭接网络［J］.施工技术，1993，22（3）：29-30.

［22］赵铁生.双代号搭接施工网络计划研究［J］.基建优化，1985，6（4）：55-58.

［23］佟鹤晶，乞建勋.搭接网络向双代号网络的转化［J］.技术经济，2009，28（10）：125-128.

［24］闫瑾，张奉举，闫睿.单代号搭接网络模糊工期的计算方法［J］.河南城建高等专科学校学报，2000，9（3）：23 -24.

［25］杨冰.网络计划计算模型的统一［J］.系统工程理论与实践，2002，03：51-55.

［26］魏道升，张智洪.搭接网络计划在公路和桥梁施工项目管理中的应用［J］.2001，1（3）：48-50.

［27］李金云.搭接网络计划时间参数计算方法的改进［J］.建筑科学，2009，21（02）：88-91.

［28］黄彬，孟国勇.工程搭接网络计划浅议［J］.大众科技，2009，14（2）：75-77.

［29］张照煌，梁会森.搭接网络计划工作总时差计算方法［J］.应用基础与工程科学学报，2009，17：151-157.

Tresearch on Path Lengths Paradox and Its Characteristics Under Spliced Network

KAN Zhi-nan1，KONG Feng1，2，QI Jian-xun1
（1.Economics and Management School of North China Electric Power University，Beijing 102206，China；2.Economics and Management School of North China Electric Power University（Baoding），Baoding 071003，China）

A paradox in spliced network is found in this paper，that is when adding a time constraint but in two different types between activities may produce different longest path.A whole new presentation of spliced network is given by studying the paradox.The new spliced network presentation is quite simple but also unified with the classic CPM network in forms.This unification not only helps to solve the problems of how to calculate the time parameters，activity floats and how to find the critical path in spliced network，but also makes extension of the theory found in CPM network to spliced network becomes possible.For example，the activity total float Tijequals to the critical path lengthminus the longest path lengththrough activity（ij），that is（-）；the sum of activity free float of any pathμequals to the critical path lengthμ-∇minus the length of this pathμ-，that is-μ-）.By using these extended theory，three convenient methods are designed to detect the difference of critical and sub-critical path lengths and to find out the sub-critical path.These methods are illustrated both effective and convenient in spliced network applications.

spliced network；longest path；activity floats；CPM network

C931

：A

1003-207（2014）05-0121-10

2012-07-05；

2013-05-06

国家自然科学基金资助项目（711171079）

阚芝南（1987-），女（汉族），江苏扬州人，华北电力大学经济与管理学院博士生，研究方向：管理科学与工程.