内生时机下多阶段R&D博弈的均衡行动顺序

杨晓花，夏火松，谷 伟，陈文磊

内生时机下多阶段R&D博弈的均衡行动顺序

杨晓花1，夏火松1，谷 伟2，陈文磊3

基于内生时机的博弈理论，研究了内生的R&D时机下双寡头企业先进行R&D活动后进行产品市场价格竞争的多阶段动态博弈的均衡R&D顺序，其中产品市场上的需求函数是线性的且企业在产品市场上的行动是同时进行的。运用逆向归纳法研究表明均衡R&D顺序只由企业的R&D外溢水平决定：若两企业的外溢水平都较低（较高），则均衡R&D顺序为两企业同时行动（分别以两企业为领头者的序贯行动）；若一个企业的外溢水平较低而另一企业的外溢水平较高，则均衡R&D顺序为以低外溢水平的企业为领头者的序贯行动。在序贯R&D时两企业的R&D总水平、社会总福利水平及产品市场产量（价格）都高于（低于）同时R&D时的情形。

内生时机；R&D；外溢；均衡

1 引言

寡头企业策略性R&D竞争往往是一个既包括R&D策略又包括产品市场策略的多阶段博弈问题。在这种博弈中企业往往先进行R&D竞争后在产品市场进行竞争，由于企业R&D的目的是为了产品市场上获得更大的收益，同时由于产品市场上的策略又影响企业的R&D决策，因此其均衡结果往往不同于单一产品市场竞争或单一R&D竞争时的均衡。

对这种企业间先进行R&D竞争后在产品市场竞争的博弈已有研究主要是从两个大的方面进行的：第一方面主要研究不同的R&D组织形式或外溢形式对均衡R&D水平及企业收益的影响。这一类研究基本以d'Aspremont［1］的研究为基础。d' Aspremont［1］研究了两企业首先同时合作或非合作的选择R&D投入，然后在产品市场上进行Cournot竞争的两阶段动态博弈模型，比较了在两种情况下均衡的相对技术改进量及产品产量，并把它和两阶段都完全垄断的情况做了比较。Kamien等［2］对d' Aspremont［1］的研究进行了扩展与推广：将竞争的企业由两个推广到n个；R&D进行的方式推广到完全竞争、R&D卡特尔、合资研究中心及合资卡特尔。孙树磊［3］则放松了d'Aspremont［1］对模型的对称性假设，研究了不同的R&D形式下企业的均衡行为。Kamien等［4］还研究了既存在R&D竞争又存在产品市场竞争的多阶段博弈中R&D方法和R&D预算对企业的吸收能力的影响。方海燕和达庆利［5］研究了这类博弈中不同R&D形式下的市场绩效。方海燕和达庆利［6］还研究了同时存在政府R&D补贴时这类多阶段博弈中，企业采用不同R&D形式时政府的最优补贴率。Amir［7］在d' Aspremont［1］的模型的基础上，运用超模博弈的方法，考察了当外溢只由R&D产出较高的企业溢向R&D产出较低的企业，而产品市场上的竞争为一般情形时的两阶段双寡头博弈情形。Amir等［8-9］讨论了内生外溢时（即技术外溢率由企业内部决定）不同形式的R&D合作下的最优R&D绩效。刘卫民［10］研究了内生外溢下政府对研发合作的激励问题。张春辉和陈继祥［11］则在有限理性的假设下研究了这种多阶段博弈中内生溢出和R&D投入对创新模式的影响。候光明［12］比较了混合外溢时（即外生外溢和内生外溢时）合作与非合作R&D的均衡。

第二方面则主要研究产品市场上为不同竞争形式时整个博弈均衡的差异性。这一方面的研究以Qiu［13］为基础。Qiu［13］比较了企业先进行完全竞争的过程R&D活动后在产品市场上竞争的两阶段博弈中当产品市场分别为价格和产量竞争时博弈的均衡。Symeonidis［14］研究了类似的两阶段博弈中当企业的R&D活动为产品R&D时产品市场为两种不同竞争形式时均衡的差异性。Lin Ping等［15］研究了差异产品时过程R&D和产品市场竞争并存时产品市场不同竞争形式时的均衡。另外Leahy和Neary［16-17］则分别研究了在策略性外贸活动中，政府对先进行R&D活动后在产品市场上和国外企业竞争的企业的最优补贴政策和产业政策。这一类已有研究中为了对两种不同竞争形式下的比较有具体结果往往假定企业的外溢水平是相同的，且企业的R&D成本函数多为给定的二次成本函数。这一类研究的实质是考察在存在R&D竞争的动态环境中价格与产量两种竞争形式的相对效率。研究结果表明产品市场上不同的竞争形式对R&D活动的影响是不同的。同时这一类对既存在R&D又存在产品市场竞争的多阶段博弈的已有研究中基本都假定企业的R&D活动及产品市场竞争分别是在两阶段内同时进行的，即R&D阶段和产品市场竞争阶段每阶段内企业的行动顺序均为外生给定的同时行动。Amir［18］比较了R&D阶段外生序贯行动和同时行动时的均衡，但Amir的研究中产品市场为单一的产量竞争。

博弈中行动顺序外生给定这一假设一直以来广受学者们的置疑。Hamilton和Slutsky［19］指出博弈中参与人的行动顺序本身是理性参与人博弈的结果，即博弈中参与人的行动顺序本身应由参与人内生决定，并给出两种具体确定参与人博弈顺序的规则——可观测延迟和行动承诺。在Hamilton和Slutsky［20-23］的研究的基础上，学者们对内生时机下传统价格和产量竞争中的均衡行动顺序进行了广泛研究。这些研究中企业只进行单一的产品市场竞争，而不存在其它方面竞争。

正如内生时机观点强调的，企业对行动时机的选择往往是由其利益决定的，在企业既存在R&D竞争又存在产品市场竞争的博弈中，不同企业的R&D活动往往并非同时进行，有些企业倾向于在R&D活动中先发制人，而有些企业则倾向于先观测别人的行动后根据别人的行动采取行动。在已有研究的基础上，本文在非对称外溢及一般的R&D成本函数下，考察了既存在R&D活动又存在产品市场竞争的多阶段双寡头博弈中当企业的R&D活动顺序由企业按可观测延迟的规则内生决定，且产品市场竞争为Bertrand竞争时的均衡行动顺序。

2 可观测延迟的内生时机规则

由于博弈中参与人的行动时机也由参与人内生确定的这一观点更符合非合作博弈中“理性参与人以最大化自己的收益为目的”的这一基本假设。本文研究可观测延迟的内生R&D时机下既存在R&D竞争又存在产品市场竞争的多阶段博弈的均衡，为此首先简单介绍Hamilton和Slutsky［20-23］给出的可观测延迟的内生时机规则。

在对内生时机博弈的研究中，通常称对应的外生时机博弈为基本博弈。按这种称呼任何一个两人博弈的基本博弈实质上包含三个博弈，一个同时行动博弈和两个序贯行动博弈，如在价格竞争中基本博弈实质表示同时行动的价格竞争和分别以两个参与人为领头者的序贯博弈。可观测延迟的内生时机博弈规定在基本博弈之前参与人先就基本博弈中的行动顺序进行博弈——同时选择在基本博弈中的行动阶段。参与人同时选择行动顺序的这个阶段称为基本博弈的扩展的阶段。在扩展的阶段如果两参与人都选择在基本博弈中先动（或后动），则基本博弈中的行动顺序为两参与人同时行动；如果两参与人分别选择在基本博弈中先动和后动，则基本博弈中的行动顺序为序贯行动，且行动顺序按参与人在扩展阶段中所选择的行动顺序进行。按这种内生时机机制任何一个基本博弈都可扩展为两个大的阶段——参与人关于行动顺序选择的扩展阶段和基本博弈阶段。在基本博弈之前参与人在扩展的阶段中的选择为所有参与人观测到，且若在扩展的阶段参与人选择在基本博弈中进行序贯行动，则在基本博弈中后行动者可观测到先行动者的行动。因此整个扩展的博弈为一个完全信息的动态博弈，其均衡概念为子博弈精炼Nash均衡。本文只考虑纯策略均衡，而不考虑混合策略均衡。整个博弈的任何一个子博弈精炼Nash都对应着基本博弈中的一个行动顺序，该行动顺序即为内生行动机制下博弈的均衡行动顺序。

若记同时行动的基本博弈中参与人i的均衡（Nash均衡）支付为，而序贯行动的基本博弈中参与人i作为领头者和尾随者时的均衡支付（子博弈精炼均衡）分别为和。由于整个包含内生时机的扩展的博弈为完全信息的动态博弈，采用逆向归纳法，给定参与人在基本博弈中的支付由其均衡支付代替，参与人在扩展的阶段关于行动顺序的选择可简化为如下的2×2博弈：

图1 参与人关于行动顺序选择的博弈

其中E表示在基本博弈中先动，而L表示在基本博弈中后动。

下面介绍上述内生时机规则下企业先进行R&D竞争后进行产品市场价格竞争的博弈（后面简记为R&D/Bertrand竞争）的基本模型及假设。

3 基本模型及假设

在R&D/Bertrand竞争的多阶段博弈中，很多因素都可能影响内生R&D时机下的均衡，如R&D活动的组织形式、R&D的功能、外溢的水平、R&D成本函数、产品市场上的竞争形式、产品市场上的需求及成本函数等。本节讨论的R&D/Bertrand竞争博弈中假设企业在第一阶段的R&D活动是完全竞争的，R&D活动以确定的形式减少企业的单位生产成本；企业在产品市场上的竞争是同时进行的，且代表性消费者的效用函数为：

其中qi为企业i的产量（i=1，2），b∈（0，1）为产品的差异程度。

在此效用函数下市场逆需求函数为：

其中i，j=1，2，i≠j，a为初始需求，且a＞c。

在（1）式给出的逆需求函数下市场的需求函数为：

另外不同于以往的研究本章的研究中企业的外溢水平是不同的，且企业的R&D顺序由企业内生确定。假设企业i的初始单位生产成本相同都为c，R&D活动以确定的形式减少单位生产成本c，R&D成本函数为：

fi（·）：［0，∞］→［0，c］，其中i=1，2；

假设两企业的外溢水平分别为β1和β2，βi∈［0，1］，βi=0表示R&D为完全专用的，而βi=1表示R&D为完全公用品。在以上假设下若企业i的 R&D投入为fi（xi），则其有效的单位成本减少量为：

xi+βjxj，i，j=1，2，i≠j

其中xi为自身的R&D投入带来的单位成本减少量，而βjxj为对手R&D投入的外溢带来的单位成本减少量。

值得说明的是，这里即使企业内生选择在R&D阶段序贯行动，仍然假设外溢是双向的，这是因为外溢不仅体现了企业自身的保密程度，更体现了企业在R&D活动上的交叉学习机会，当企业序贯R&D时，这种双向外溢可以理解为企业先进行R&D决策，当两企业的R&D决策都确定后实际的R&D活动才会发生。

在内生的R&D顺序下企业之间的R&D/Bertrand竞争博弈分为三个大的阶段。首先，在第一阶段企业内生确定R&D阶段的行动顺序，其内生确定R&D顺序的行动规则为第2节中所介绍的可观测延迟的内生时机。其次，在第二阶段，观测到内生确定的R&D阶段的行动顺序，企业按这种行动顺序进行R&D投资。事实上，若企业内生确定在R&D阶段序贯行动，该阶段便包括两个R&D阶段（从而整个博弈为一个四阶段博弈）。最后，在第三阶段，观测到关于行动顺序和具体R&D支出水平的决策后，企业在产品市场上同时进行价格竞争。由于企业在每阶段行动时可以观测到之前阶段的所有行动，给定企业在R&D阶段的行动顺序确定，若企业i在R&D阶段的投入为fi（xi），则产品市场价格竞争时企业的策略为pi（xi，xj）。整个博弈为完美信息的动态博弈，其均衡为子博弈精炼Nash均衡。

在上述内生时机下，所有可能的均衡对应于R&D阶段的三种不同的行动顺序，分别为同时行动和两种领头者-尾随者式的序贯行动。记企业在R&D阶段选择同时行动时所对应的后续基本两阶段博弈为G；而在R&D阶段选择以i为领头者的序贯行动时所对应的后续基本博弈为Gi，i=1，2，Gi是一个包含序贯R&D和产品市场价格竞争的三阶段博弈。记博弈G中两企业的均衡R&D水平为（，），产品市场上的均衡价格为（，）。同时记博弈Gi中两企业的均衡R&D水平为（，），产品市场的均衡价格为（，）。其中N表示Nash，而L和F分别表示领头者（leader）和尾随者（follower）。值得说明的是即使企业选择在R&D阶段同时行动，整个包含内生时机的博弈仍然是一个三阶段的动态博弈，其解仍然是子博弈精炼均衡，因此这里的上标只是对应于R&D阶段的情形。

由上述关于基本模型的介绍，给定企业在R&D阶段的行动顺序确定，若企业i在R&D阶段的投入为fi（xi），其中xi∈［0，c］，在产品市场上的价格为pi，则企业i在产品市场竞争时面临的收益函数为：

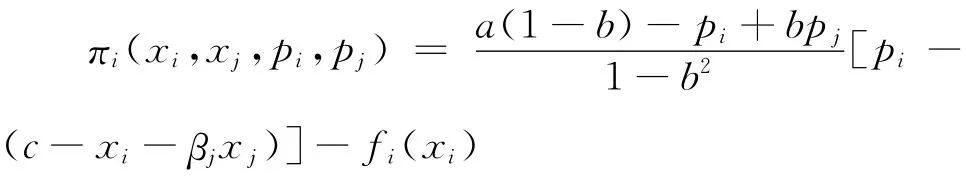
由于企业在产品市场上行动时可以完全观测到之前阶段的所有行动且产品市场上企业是同时行动的，运用逆向归纳法及一阶条件=0，企业i在产品市场上的定价策略pi（xi，xj）为：

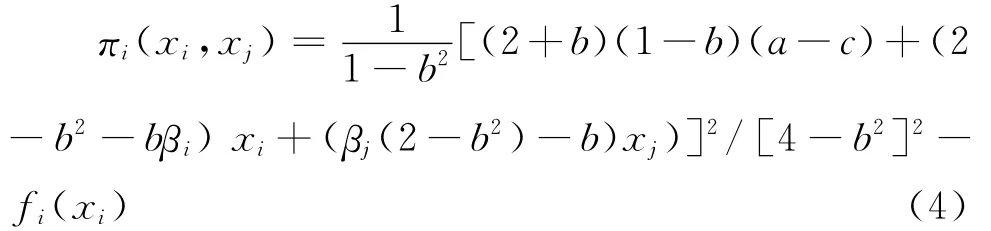
若内生时机结果确定企业在R&D阶段进行以i为领头者的序贯R&D，即参与人之间进行基本博弈Gi，则显然由（4）式此时参与人j在R&D阶段的反应函数rj：［0，c］→［0，c］由

因此若内生时机结果确定两企业在R&D阶段同时行动，即参与人之间进行基本博弈G，则企业i在R&D阶段的收益函数为：

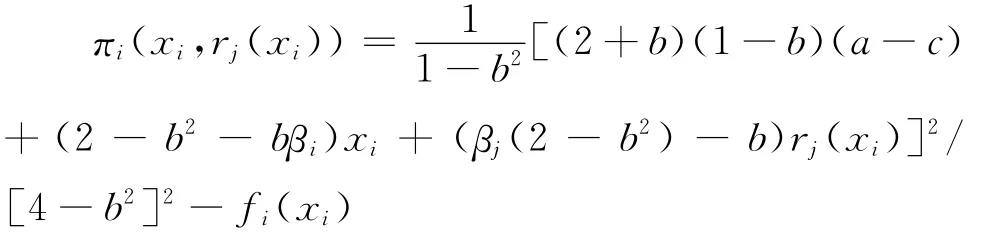
下面为分析内生时机下的均衡行动顺序，给出如下基本假设：

假设1：fi（·）为严格递增的二次连续可微函数，且fi（0）=0；

假设2：a（2-b-b2）-c（2-b2）（1-βi）＞0；

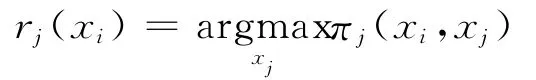
因此此时参与人i在R&D阶段的收益函数为：确定，具体的

假设4：对于∀x∈［0，c］，fi″（x）＞。

下面逐一对以上假设进行说明。假设1是平凡的。假设2其实只有在βi（2-b2）-b＜0时才是必要的，它要求初始需求足够大，是为了保证在产品市场上所有企业都会进行生产，即产品市场上的内点解存在。事实上由（2）及（3）式企业i在产品市场上的产量为：

qi（xi，xj）=［（a-c）（2-b-b2）+（2-b2-bβi）xi+（βj（2-b2）-b）xj］/［（1-b2）（4-b2）］

显然qi（xi，xj）关于xi是总是递增的。当βi（2 -b2）-b＞0时，qi（xi，xj）关于xj也是递增，因而此时对于任意的xi∈［0，c］都有qi（xi，xj）＞0；当βi（2-b2）-b＜0时，qi（xi，xj）关于xj是递减的，因此此时只要qi（0，c）＞0就有qi（xi，xj）＞0，而假设2即保证了qi（0，c）＞0。假设3实质是Inada条件，它要求当R&D投入较小时，R&D边际成本增长的速度较小，而当R&D投入较大时边际成本会快速增长。这是符合现实的，现实中当企业的生产效率较低时往往很容易减少生产成本，而当企业的生产成本本身已经很小时往往就很难再减少了。假设4要求R&D成本函数足够凸，它是为了保证企业在R&D阶段所面临的利润函数满足一定的凹性条件，从而不致于使企业在R&D后的边际成本为零或负值。假设3和假设4共同保证了在R&D阶段所有的企业都会进行R&D，即R&D阶段的均衡存在。

4 内生R&D时机下R&D/Bertrand竞争的多阶段博弈的均衡

有了上述基本模型及假设，关于上述多阶段博弈首先有如下的关于解的存在性结论：

命题1 在假设1-4下，上述基本博弈G及Gi中的解存在。

证明：首先注意到参与人有效的策略空间为：

X=｛（x1，x2）：x1+β2x2≤c，x1+β2x2≤c，xi≥0，i=1，2｝

其次由（4）式有：

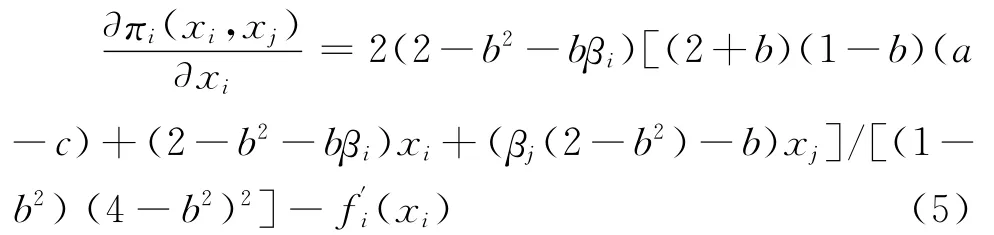
所以：

（2）若βi＞b/（2-b2），i=1，2，则ri（·）在［0，x-j］上严格递增，在［x-j，c］上ri（xj）=c-βjxj，从而严格递减。且ri（·）的曲线总在曲线xi=x-i之下，即∀，其中＜0，又πi（xi，xj）在策略空间上连续，所以基本博弈G中解存在。又因为上述有效的策略空间为紧的，所以基本博弈Gi中的解也存在［24］。

其次，关于参与人的最优反应函数ri（xj）=由方程组确定，其实质是一个边界条件）。

（3）若βi＞b/（2-b2）＞βj，其中i，j=1，2，i≠j，则ri（·）严格递减，rj（·）在［0，］上严格递增，在［，c］上ri（xj）=c-βjxj，从而严格递减。

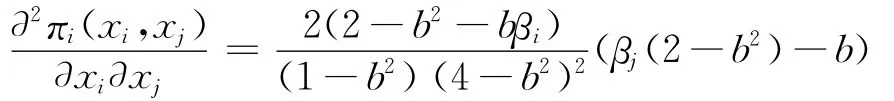
因此当βi＜b/（2-b2）时＜0，即结论（1）成立。

（2）若βi＞b/（2-b2），则显然ri（·）先递增，当到达边界直线的交点时，在，c］上ri（xj）=cβjxj，从而严格递减。另外由于ri（·）先增后减所以其在xj=处达到最大值。所以要证∀xj，ri（xj）＜，只证ri（）＜。又0，而。所以由假设3，。而，所以。即（2）得证。

（3）由结论（1）及（2）的证明，结论（3）是显然的。

上述关于参与人在R&D阶段的反应函数的结论可直观上表示如下：

图2 （a） βi＞b/（2-b2）

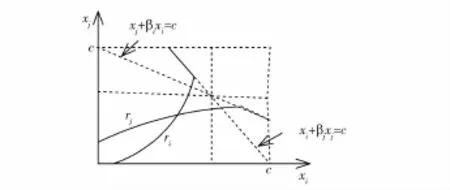
图2 （b） βi＞b/（2-b2）

图2 （c） βi＞b/（2-b2）βj

有了上述关于反应函数单调性的结论，下面给出本节的主要结论：

命题3 （1）若βi＜b/（2-b2），i=1，2，则企业在R&D阶段的内生时机结果为同时行动，即R&D/Bertrand竞争的均衡结果为博弈G。

（2）若βi＞b/（2-b2），i=1，2，则企业在R&D阶段的内生时机结果为两种序贯行动，即R&D/Bertrand竞争的均衡结果为博弈G1和G2。

（3）若βi＞b/（2-b2）＞βj，i，j=1，2，，i≠j。则企业在R&D阶段的内生时机结果为以企业j领头的序贯行动，即R&D/Bertrand竞争的均衡行动结果为博弈Gj。

证明：（1）若βi＜b/（2-b2），i=1，2，则显然由（4）式有，又，其中第一个不等式是由于Stackelberg领头者的支付大于Nash均衡支付，第二个不等式是由Nash均衡的性质，因此即。又由命题2的结论（1），rj（·）为严格递减的，所以。所以）。其中第一个不等式也是由Nash均衡的性质，而第二个不等式是因为，即。所以由第2节中的关于内生时机时的图1，显然均衡结果为博弈G。

（2）若βi＞b/（2-b2），i=1，2，则显然由（4）式有，而ri（·）在［0，］上严格递增且∀xj，ri（xj）＜。又由于。所以，即）。所以。所以，即。同理由第2节中关于内生时机时的图1，显然均衡结果为博弈G1和G2。

（3）若βi＞b/（2-b2）＞βj，i，j=1，2，i≠j，则对于i的分析类似于结论（2）中的证明而对于j的分析类似于结论（1）中的证明，即有），而。所以均衡结果为博弈Gj。

上述结果表明，在内生的R&D顺序下，多阶段博弈的均衡行动顺序与R&D效率无关，而只与外溢水平和产品的差异程度相关。当两企业的外溢水平都较低时，两企业都偏好于做领头者，并且宁愿同时行动也不愿做尾随者，因此此时企业在选择R&D时机时都会选择先动而最终导致同时行动；当两企业的外溢水平都较高时，企业的尾随者支付高于其Nash均衡支付，因此此时会导致两种序贯行动；当一个企业的外溢水平低于b/（2-b2），而另外一个企业的外溢水平高于b/（2-b2）时，低外溢水平的企业宁愿同时行动也不愿充当尾随者，而高外溢水平的企业宁愿做尾随者也不愿同时行动，因而最终导致以低外溢水平的企业为领头者的序贯行动。这说明外溢水平在决定企业的行动顺序时起着至关重要的做用，是符合现实的。

进一步的，当外溢较高时基本博弈中的均衡R&D水平、价格、产量及社会总福利水平有如下结论：

推论1 若βi＞b/（2-b2），i=1，2，则：

（1）X（Gi）≥X（G），其中X（Gi）=X（G）=，分别表示基本博弈Gi及G中的均衡R&D总水平。

（2）pi（Gi）≤pi（G），pj（Gi）≤pj（G）；qi（Gi）≥qi（G），qj（Gi）≥qj（G），即每个企业在基本博弈Gi中的价格（产量）都低于（高于）其在G中的价格（产量）。

（3）W（Gi）≥W（G），i=1，2。其中W（Gi）表示基本博弈Gi中的社会总福利，它等于消费者剩余和生产者利润之和。

证明：（1）由命题3的证明若βi＞b/（2-b2），i =1，2，则，所以（1）显然成立。

（2）由（3）式企业的均衡定价策略pi（xi，xj）关于xi及xj递减，而由（2）及（3）式均衡处企业的产量为：

显然对∀b、β∈（0，1）有2-b2-bβi＞0，即qi（xi，xj）关于xi为递增的；而当βi＞b/（2-b2），i =1，2时，显然qi（xi，xj）关于xj也是递增。所以由结论（1）结论（2）成立。

（3）由于社会总福利为消费者剩余和生产者利润之和，即：

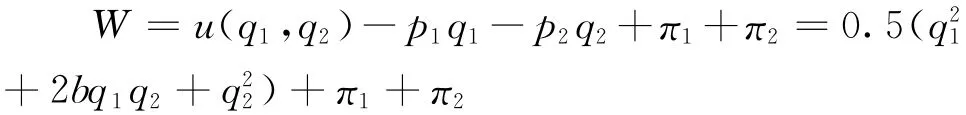
上述结论说明当外溢水平较大时，企业的内生行动结果为序贯行动，而序贯行动所带来的R&D水平、社会总福利及企业的利润较同时行动时的相应量都要大（对于企业的利润见命题3中（2）的证明）。

5 算例分析

为了使上述结论更直观，我们进一步通过图形来研究内生时机下的均衡R&D结果。由于我们主要是研究内生的R&D时机对博弈均衡的影响，因此假设产品市场上的参数是固定的。具体的假设a =2，b=1/2，c=1，，i=1，2。同时理论研究表明均衡只与R&D外溢水平有关，因此下面将通过图形比较不同外溢水平下不同行动顺序博弈中的均衡R&D水平。

对于给定的产品市场上的以上参数，企业在R&D阶段的利润函数为πi（xi，xj）=64［5/4+（7/4-βi/2）xi+（7βj/4-1/2）xj］2/675-2xi2，序贯行动中的反应函数为：

通过复杂计算及MATLAB仿真，下面图3（a）给出了单个企业分别在不同行动顺序博弈中的均衡R&D水平的比较，即x1（G）和x1（G1）。而图3（b）则给出了不同行动顺序博弈中两企业总的均衡R&D水平的比较，即X（G）和X（G1）。

图3 （a） 单个企业在不同行动顺序博弈中均衡R&D水平的比较

通过图3（a）容易看出，虽然当外溢水平不同时两平面有交叉，但当外溢水平都较大时曲面x1（G1）显然在曲面x1（G）之上，这表明当外溢水平较大时内生序贯行动中企业的R&D投入要高于同时行动，与上文中的结论是一致的。

很显然图3（b）表明在所给定的产品市场参数下，序贯行动中的总R&D水平总是要高，这与文中的结论也是相符的。

图3 （b） 企业在不同行动顺序博弈中总R&D水平的比较

进一步的若假设βi=βj=0.75，则经过繁琐的计算=0.157，=0.099，=0.095，所以显然有≥，x≥。X（Gi）=+=0.256＞X（G）=+=0.190。而，所以显然此时内生R&D时机下为序贯行动。此时对于产品市场上pi（Gi）=0.030，pj（Gi）=0.654，而pi（G）= 1.223，所以显然有pi（Gi）≤pi（G），pj（Gi）≤pj（G）；qi（Gi）=0.550，qj（Gi）=0.538，而qi（G）=0.518，所以有qi（Gi）≥qi（G），qj（Gi）≥qj（G）。另外，对于社会福利有W（Gi）=0.827＞0.768=W（G）。

6 结语

内生的R&D时机在理论上更符合博弈中参与人理性的基本假设，在实际上由于企业的R&D活动往往是自主进行的从而也更符合社会现实。内生R&D时机下企业先进行R&D后在产品市场上进行价格竞争的多阶段博弈的均衡R&D顺序只由企业的R&D外溢水平决定，和企业的R&D成本函数无关。具体地，若两企业的外溢水平都较低，则均衡的R&D顺序为两企业同时行动；若两企业的外溢水平都较高，则均衡的R&D顺序为分别以两个企业为领头者的序贯行动；若一个企业的外溢水平较低而另一个企业的外溢水平较高，则均衡的R&D顺序为以低外溢水平的企业为领头者的序贯行动。在序贯R&D时两企业的R&D总水平、社会总福利水平及产品市场产量（价格）都高于（低于）同时R&D时的情形。这说明内生时机下仅仅通过诱导高的外溢水平可以诱导企业进行高的R&D投入同时也可以增加社会福利。

［1］d'Aspremont C，Jacquemin A.Cooperative and noncooperative R&D in duopoly with spillovers［J］.American Economic Review，1988，78：1133-1137.

［2］Kamien M，Muller E，Zang I.Research joint ventures and R&D cartels［J］.American Economic Review，1992，82：1293-1306.

［3］孙树磊，生产与研发成本差异下双寡头横向R&D合作［J］.中国管理科学，2008，16（10）：63-67.

［4］Kamien M，Zang I.Meet me halfway：Research joint ventures and absorptive capacity，International Journal of Industrial Organization［J］.2000，18（7）：995-1012.

［5］方海燕，达庆利.存在研发投资溢出时的企业市场绩效分析［J］.中国管理科学，2008，16（S1）：556-560.

［6］方海燕，达庆利.基于差异产品的政府最优R&D补贴策略研究［J］.中国管理科学，2009，17（3）：165-172.

［7］Amir R.Modelling imperfectly appropriable R&D via spillovers［J］.International Journal of Industrial Organization，2000，18（7）：1013-1032.

［8］Amir R，Wooders J.One-way spillovers，endogenous innovator/Imitator roles，and research joint ventures［J］.Games and Economic Behavior，2000，31（1）：1-25.

［9］Amir R，Evstigneev I，Wooders J.Noncooperative R&D versus cooperative R&D with endogenous spillover rates［J］.Games and Economic Behavior，2003，42（2）：183 -207.

［10］刘卫民，陈继祥.内生溢出与R&D竞争、合作的激励问题［J］.管理工程学报，2006，20（3）：1-5.

［11］张春辉，陈继祥.考虑内生溢出与R&D投入的创新模式选择［J］.中国管理科学，2011，19（3）：26-32.

［12］侯光明，艾凤义.基于混合溢出的双寡头横向R&D合作［J］.管理工程学报，2006（20），4：94-97.

［13］Qiu L D.On the dynamic efficiency of Bertrand and Cournot equilibria［J］.Journal of Economic Theory，1997，75（1）：213-229.

［14］Symeonidis G.Comparing Cournot and Bertrand equilibria in a differentiated duopoly with product R&D［J］.International Journal of Industrial Organization，2003，21（1）：39-55.

［15］Lin Ping，Saggi K.Product differentiation，process R&D and the nature of market competition［J］.2002，46（1）：201-211.

［16］Leahy D，Neary J P.Public policy toward R&D in oligopolistic industries［J］.American Economic Review，1997，87：642-662.

［17］Neary J P，Leahy D.Strategic trade and industrial policy towards dynamic oligopolies［J］.Economic Journal，2000，110（463）：484-508.

［18］Amir M，Amir R，Jin J.Sequencing R&D decisions in a two-period duopoly with spillovers［J］.Economic Theory，2000，15（2）：297-317.

［19］Hamilton J，Slutsky S.Endogenous timing in duopoly games：Stackelberg or Cournot equilibria［J］.Games and Economic Behavior，1990，2：29-46.

［20］van Damme E，Hurkens S.Endogenous Stackelberg leadership［J］.Games and Economic Behavior，1999，28（1）：105-129.

［21］van Damme E，Hurkens S.Endogenous price leadership［J］.Games and Economic Behavior，2004，47（2）：404-420.

［22］AmirR，Grilo I.Stackelberg versus Cournot equilibrium［J］.Games and Economic Behavior，1999，26（1）：1-21.

［23］Amir R，Stepanova A.A second-mover advantage and price leadership in Bertrand duopoly［J］.Games and E-conomic Behavior，2006，55（1）：1-20.

［24］Hellwig M，Leininger W.On the existence of Subgame-Perfect Equilibrium in infinite-action games of perfect information［J］.Journal of Economic Theory，1987，43（1）：55-57.

（1.武汉纺织大学管理学院，湖北武汉 430074；2.中南财经政法大学统计与数学学院，湖北武汉 430074；3.武汉大学经济管理学院，湖北武汉 430072）

Equilibrium Move Order of Multi-Period R&D Game under Endogenous Timing

YANG Xiao-hua1，XIA Huo-song1，GU Wei2，CHEN Wen-lei3
（1.School of Management，Wuhan Textile University，Wuhan 430074，China；2.School of Statistics and Mathematics，Zhongnan University of Economics and Law，Wuhan 430074，China；3.Economics and Management School，Wu Han University，Wuhan 430072，China）

Based on endogenous timing game theory，the equilibrium move order of R&D is studied in this paper in a multi-stage game in which firms R&D are followed by competition in product market，with the assumption that in product market the demand function is linear and the move-order is simultaneously. With backward induction it is shown that，equilibrium R&D order is only decided by firms'R&D spillover.When both firms'spillover rates are low（high），the equilibrium R&D order is simultaneous play（sequential play with both leader-follower configurations）.When one firm's spillover rate is low and the other's is high the equilibrium R&D order is sequential play with the low-spillover-rate-firm as the leader. When equilibrium R&D order is sequential play the total R&D level，the social welfare and the output（price）in product market are（is）higher（lower）than simultaneous R&D.

endogenous timing；R&D；spillover；equilibrium

F273

：A

1003-207（2014）05-0083-08

2011-10-24；

2013-09-21

国家自然科学基金资助项目（71171153）；湖北省教育厅一般项目（2011jyty024）

杨晓花（1979-），女（汉族），湖北人，武汉纺织大学管理学院副教授，博士，研究方向：博弈论及决策理论.