基于正交试验的等弦波形管热工性能分析

吴金星，李俊超，王 力，刘青锋，贺 敏，李国立

(1.郑州大学化工与能源学院，河南 郑州 450001;2.机械工业第六设计研究院有限公司，河南郑州 450007;3.河南力威热能设备制造有限公司，河南郑州 450101)

0 引言

换热管是锅炉、管壳式换热器等设备中重要的换热元件，长期以来多采用光滑直管。但光滑直管存在换热效率较低、管材耗量大等缺点，因而众多学者对换热管强化做了大量研发工作［1－3］。换热管的强化传热方法大体有两种，一种是在管内插入内插物(如纽带、静态混合器等)，通过改变管内流体流态达到强化传热的目的，但流阻显著增加;另一种是改变换热管的内外表面结构(如缩放管、波纹管、螺旋槽管、横纹管等)，从而干扰或破坏流体边界层达到强化传热的目的，但多数强化管加工比较复杂［4］，制造成本较高。

真空锅炉是一种换热介质内循环、筒体内安置换热管束且保持一定真空度的特殊锅炉型式，运行时炉内介质产生蒸汽，并在管束外冷凝，将相变热传给管内自来水向外供热。可见，换热过程中热阻较大的一方是管内。

针对广泛应用于真空锅炉D=10 mm的不锈钢换热管，以降低管内热阻为目标，开发设计出等弦波形强化换热管，如图1所示，其具有连续波形结构且各段中心弧线曲率半径、圆弧弦长相等的特点。该强化管能交替改变管内流体流向，使流体反复冲刷管壁内表面，减薄和破坏流体边界层，从而达到强化传热的目的。在保证换热效率增大和流阻有限增加的基础上，需要进一步优化设计，降低加工难度，简化加工过程，使新型等弦波形强化换热管快速应用于工程中。

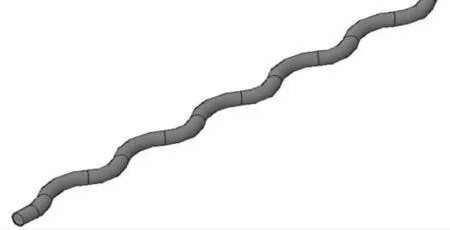
图1 等弦波形强化换热管模型

1 基于模拟正交试验的等弦波形管结构优化

文中利用Fluent数值分析软件，结合正交试验方法，来优化设计适用于真空锅炉的最佳换热管结构。

1.1 计算模型的建立

1.1.1 几何模型

等弦波形管的中心弧线长度1500 mm，管径D=10 mm，中心弧线的弦长L=40～55 mm，中心弧线的弯曲半径R=30～60 mm，采用二维模型进行数值模拟，取等弦波形管周期段模型如图2所示，忽略壁厚的影响。

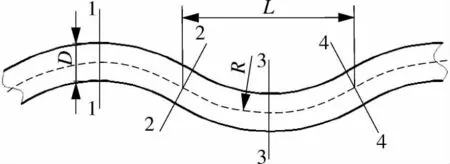
图2 等弦波形管周期段模型

1.1.2 物理模型

采用水作为工质，密度ρ=998.2 kg/m3，比热Cp=4183 J/(kg·K)，导热系数 λ =0.599 W/(m·K)，粘度 μ =0.001003 kg/(m·s)，在标准大气压下进行操作。同时作如下假设:

(1)不考虑重力影响。

(2)所有界面和接触表面不变形，液－固接触面为无滑移。

(3)流体流过管后无质量增加，管内无其他源项。管内流体的流动和热量传递满足连续性方程、动量方程以及能量方程。

1.1.3 网格划分与边界条件

用结构化网格对计算区域进行网格划分，同时对壁面附近网格进行加密处理。计算过程采用标准k—ε方程湍流模型;压力速度的耦合采用Simple算法。迭代运算过程中，能量方程残差控制在10－6数量级，其余方程组残差控制在10－4数量级。

入口边界:依据真空锅炉实际工程情况，换热管内流体流速一般为1 m/s左右，根据功耗与速度的三次方成正比关系，为避免功耗过大，速度最大取值一般不超过2 m/s，因此，入口流速取v=0.5 ～2 m/s，对应入口雷诺数 Re=5556 ～20000，流体入口温度20℃;出口边界:出口为外界大气压;壁面边界:壁面为恒壁温95℃。

1.2 正交表的选取及模拟结果

1.2.1 正交表的选取

为了节省模拟试验次数，一般选用较小的正交表，根据本试验三因素四水平情况，即L因素取40，45，50 和 55 mm 四水平;R 因素取 30，40，50和60 mm 四水平;V 因素取 0.5，1.0，1.5 和 2.0 m/s四水平，故文中选取L16(45)正交表。同时，正交试验方案具有均匀性和全面性，即每次试验结果都从不同的角度提供有用的信息。

1.2.2 等弦波形管结构优化结果

按照正交表的试验方案，利用Fluent软件，对16种工况下的努赛尔数Nu分别进行模拟，得到结果见表1。

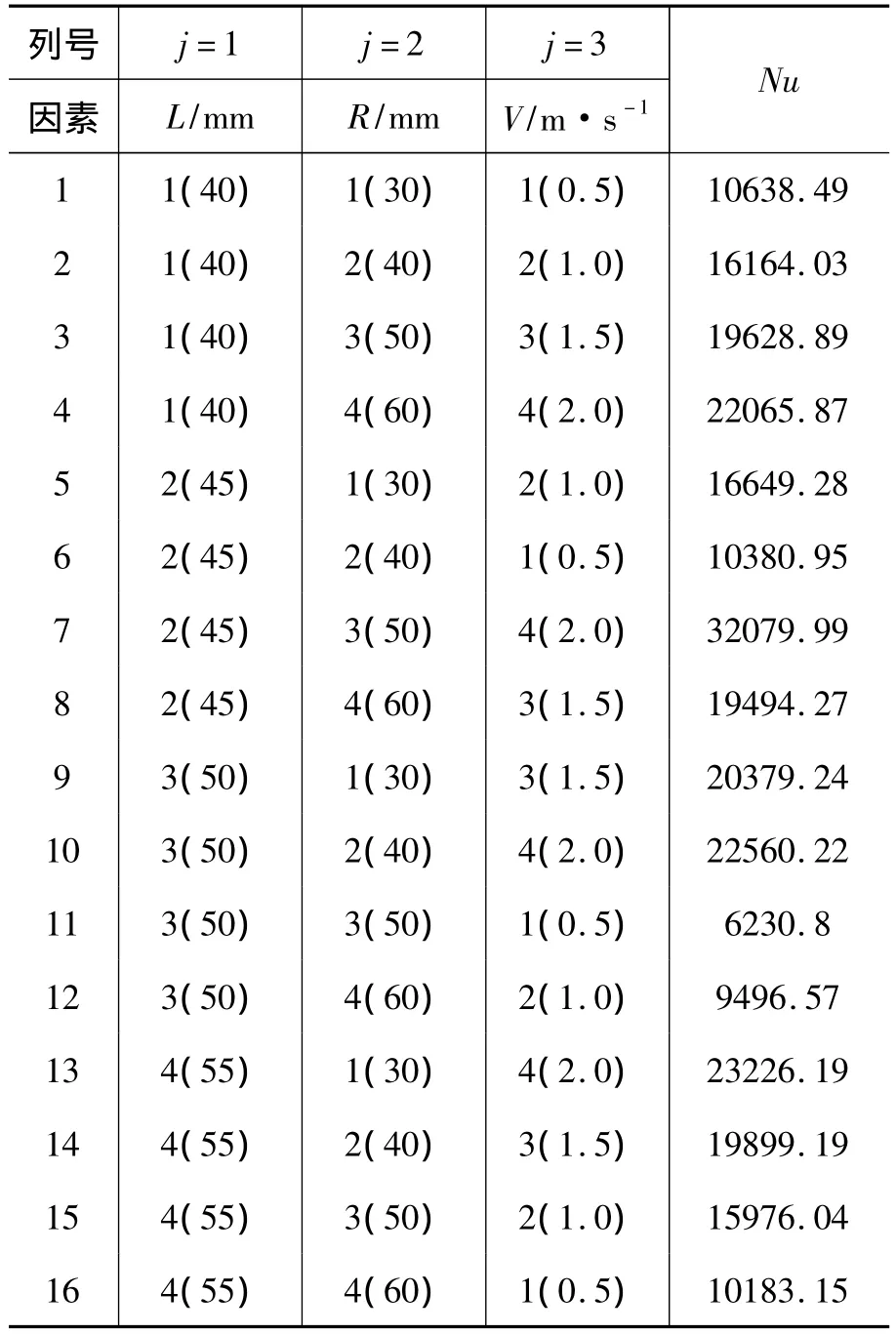
表1 试验方案及试验结果

1.3 结果分析及优化方案的确定

利用极差分析法对试验结果进行分析，得到Nu数的影响因素主次顺序及优化结构。

1.3.1 极差分析法

在表1的基础上建立表2，建立的方法为:

(1)计算各影响因素Ti的值。Ti为任一列上水平号位i(i=1，2，3，4)时所对应的试验结果之和。例如，等弦波形管中心弧线弦长L=40 mm(1水平号位)，对应的T1计算方法为将列号为1，2，3，4 对 应的 Nu 数 (10638.49，16164.03，19628.89，22065.87)相加。

(2)计算均值Mi，Mi的计算方法为将之前得到的Ti值除以水平数，即Mi=Ti/4。

(3)计算各影响因素的极差。R=max{M1，M2，M3，M4}－ min{M1，M2，M3，M4}。

表2 试验方案及试验结果分析

1.3.2 主要影响因素的确定

极差越大说明该列因素的水平改变对试验结果的影响越大。从表2可看出，极差R3＞R1＞R2，因此可以得出，Nu数的影响因素主次顺序是流速、中心弧线弦长、弯曲半径。

1.3.3 等弦波形管的结构优化

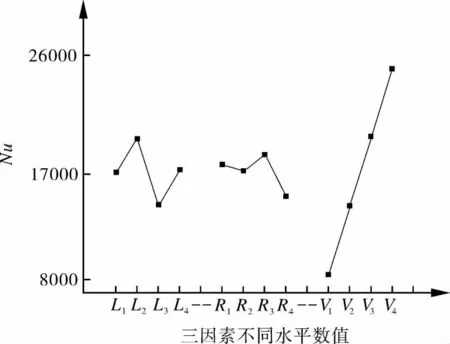
图3 Nu与三因素的关系

将3个因素的4个平均努赛尔数值画在一张图上，如图3所示。

可得出如下结论:

(1)中心弧线弦长为45 mm时，Nu数最大;

(2)中心弧线弯曲半径为50 mm时，效果最好;

(3)管内流体速度越大，对Nu贡献最大，但考虑到动力费用，最大速度取值为2 m/s。

综合起来，等弦波形强化管最优结构参数为L=45 mm，R=50 mm，使用中流体流速取2 m/s以下为最佳。

2 等弦波形管的场协同强化传热分析

2.1 场协同原理分析方法

过增元等［5］以二维平板层流边界层问题为例推导出对流换热普遍适用的方程:

式中 β——速度矢量与温度梯度之间的夹角，°

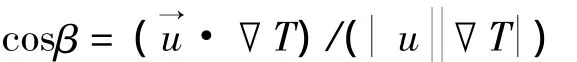
由此可见，如果在热边界层内使两矢量的点积(u·gradT)尽可能地取大值，则传热将得到强化［6］。速度与温度梯度之间的局部夹角称为协同角，研究表明［7］:速度与温度梯度的夹角应尽可能的小，协同角越小表征换热效果越好。对于等弦波形强化管，传热热阻主要存在于边界层，所以协同角的计算主要针对边界层区域。协同角的计算较为复杂，采取下式算术平均角［8］的方法进行计算:

式中 m——下标，表示整场平均

i——下标，表示所计算的区域

N——计算区域的控制容积总个数

2.2 协同角的计算与强化换热分析

等弦波形管内流体的温度场分布如图4所示。可以看出，在流体边界层区域等温线近似随管壁弯曲方向均匀变化，因此认为温度梯度垂直于管壁方向分布。

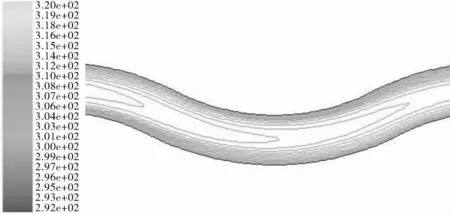
图4 等弦波形管温度场分布示意

协同角的计算主要针对单个弯曲周期具代表性的4个截面1－1，2－2，3－3，4－4(见图2)进行研究。协同角计算通过截面法向速度分量与主流速度参数确定，4个截面法向速度分量情况如图5所示。

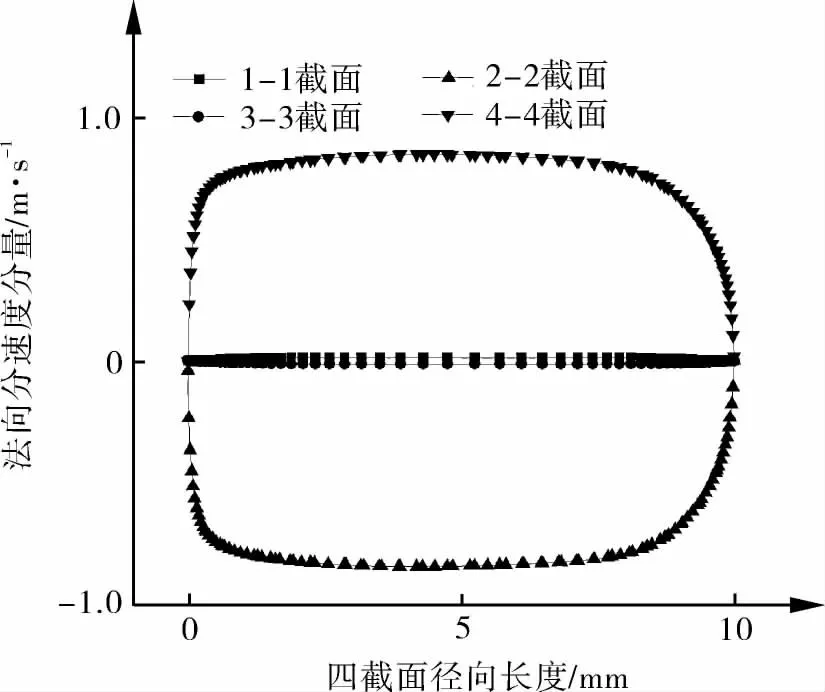
图5 4个截面法向分速度的分量图

图5示出了法向速度分量沿下壁面至上壁面的法向速度变化，可以看出，截面1－1和3－3以及截面2－2和4－4法向速度分布分别具有对称性，中心区法向速度最大，对速度方向指向壁面扰动最强烈。文中重点研究管壁附近流体边界层温度梯度与速度协同角情况，因此，利用式(3)对4个截面管壁附近分别计算协同角，计算结果如下:

(1)1－1截面上壁面附近协同角为89.766°，下壁面附近的协同角为89.852°;

(2)2－2截面上壁面附近协同角为79.16°，下壁面附近协同角为78.624°;

(3)3－3截面上壁面附近协同角为89.831°，下壁面附近协同角为89.804°;

(4)4－4截面上壁面附近协同角为78.64°，下壁面附近协同角为79.215°。

通过对直管的数值模拟计算，得出直管管壁附近协同角约为89.9997°。对比可见，等弦波形管能明显减小壁面附近温度场与速度场的协同角，局部协同角较直管减小10°以上。协同角变小，说明流体径向速度分量增大，冲刷壁面强烈，不仅能够较好地改善传热条件，而且能够减缓壁面上水垢的形成，尤其是在2－2和4－4截面附近效果最明显。

3 等弦波形强化换热管的热工性能评价

3.1 热工性能的评价方法

强化换热管的性能评价涉及多个方面，实际使用中不仅要考虑其经济性、安全性、可靠性等，更主要的是要考虑其能满足工艺条件的换热与阻力要求。

文中采用基于泵功率的评价指数J［9－10］:

式中 Nu，f——结构优化后等弦波形管的努赛尔数和压降

Nu0，f0——光滑直管的努赛尔数和压降

为突显等弦波形管的换热性能优势，与光滑直管对比，得出换热优化比率R计算公式:

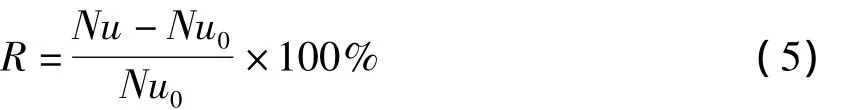
3.2 评价结果分析

数值模拟各项参数结果见表3。

表3 光滑直管与等弦波形管模拟试验参数

由表3中数值计算得出:

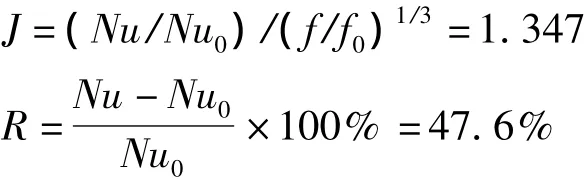
可见，评价指数J大于1，换热提高幅度R达47.6%，故等弦波形强化换热管具有较好的热工性能。

4 结论

(1)通过正交试验法并利用Fluent软件进行模拟分析，开发设计出D=10 mm的最优等弦波形强化管，得到了影响其强化换热性能的主次因素顺序为流速、中心弧线弦长、弯曲半径，最佳结构参数为中心弧线弦长L=45 mm，半径R=50 mm。

(2)试验结果表明，等弦波形管2－2，4－4截面附近区域强化传热效果较明显，且中心区法向速度最大，速度矢量指向壁面对流体扰动最为强烈。

(3)等弦波形管强化换热的原理在于减小温度场与速度场的协同角，与光滑直管相比，协同角显著减小，局部减小幅度达10°以上。

(4)强化换热管热工性能要远远优于光滑直管，换热效率可提高47.6%，在实际使用中，等弦波形管内流体强烈冲刷管壁，具有抗结垢的功效。

［1］ 许光第，周帼彦，朱冬生，等.管壳式换热器设计及软件开发［J］.流体机械，2013，41(4):38 －42.

［2］ 朱冬生，郭新超，刘庆亮.扭曲管管内传热及流动特性数值模拟［J］.流体机械，2012，40(2):63 －67.

［3］ 杨凤叶，王珂，刘彤，等.竖直管内超临界二氧化碳局部对流换热研究［J］.压力容器，2013，30(3):1－4.

［4］ 吴金星，韩东方，曹海亮.高效换热器及其节能应用［M］.北京:化学工业出版社，2009.

［5］ GUO Z Y，WANG B X.A Nolvel Concept for Convection Heat Transfer Enhancement［J］.Int J Heat Mass Transfer，1998，41(14):2221 －2225.

［6］ 赵虎城，陈占秀.正弦波纹管强化换热的场协同分析［J］.河北工业大学学报，2009，38(6):89 －92.

［7］ TAO W Q，GUO Z Y，WANG B X.Field Synergy Principle for Enhancing Convective Heat Transfer－its Extension and Numerical Verifications［J］.Int J Heat Mass Transfer，2002，45(18):3849 －3856.

［8］ 周俊杰，陶文铨，王定标.场协同原理评价指标的定性分析和定量分析［J］.郑州大学学报，2006，27(2):45－47.

［9］ 梁珍祥.凹坑凸胞板式换热器性能的数值研究［D］.郑州:郑州大学，2012.

［10］ 杨振江，杨俊兰，马一太，等.CO2跨临界水－水热泵系统模拟与试验研究［J］.流体机械，2012，40(6):61－64.