最小Q－过程的Ray－Knight紧化与Martin边界关系的实例分析*

郝淑双，徐长伟

（1.黄河科技学院信息工程学院电子系，河南郑州 450063;2.中原工学院理学院数学系，河南郑州 450007）

最小Q－过程的Ray－Knight紧化与Martin边界关系的实例分析*

郝淑双1，徐长伟2

（1.黄河科技学院信息工程学院电子系，河南郑州 450063;2.中原工学院理学院数学系，河南郑州 450007）

文中在极小转移函数Pmijin（t）诚实的条件下讨论最小Q－过程的Martin流出边界与Ray－Knight紧化的关系，并实例分析Martin流入边界与Ray－Knight紧化所添加的点之间具有一一对应关系.

最小Q－过程;Ray－Knight紧化;Martin流出边界;Martin流入边界

为解决Q过程的构造问题，需要研究Q过程的边界，将状态空间E进行紧化.最简单的紧化是单点紧化，但很多情况下仅仅用单点紧化是不够的.Doob结合马氏链的轨道引进了Martin边界，侯振挺［1］在对马氏链不加任何限制的情况下，导出了马氏链的 Martin边界及 Martin流入边界.Getoor，R.K.［2］定义E的Ray－Knight紧化珔E，上述两种紧化方法对马氏链的构造有非常重要的作用，在［3］中得出结论:在Martin流入边界有限的条件下，Martin流入边界中的点与Ray－Knight紧化所添加的点之间具有一一对应关系.本文研究最小转移函数Pminij（t）诚实的条件下最小Q－过程的Martin流出边界与Ray－Knight紧化的关系，同时结合［3］举例详细说明Martin流入边界与Ray－Knight紧化的一一对应关系.

设E={0，1，2，…}，Pij（t）（i，j∈E，t＞0）是E上诚实且标准的转移函数，Pij（t）所确定的Q矩阵Q=（qij） 全 稳 定.X=（Ω，F，Ft，Xt，θt，Px） 是Pij（t）所确定的正规链.因为Q全稳定且Pminij（t）诚实，所以Pmin

ij（t）是向后或向前方程的唯一解且是唯一的Q函数，即Pij（t）与Pminij（t）相同，故X是E上以Pij（t）为转移函数的不中断的最小Q－过程，设XT={Xτn}为X的嵌入链.首先讨论最小Q－过程的Martin流出边界与Ray－Knight紧化的关系.

1 最小Q－过程的Martin流出边界与Ray－Knight紧化

（1）最小Q－过程的Ray－Knight紧化.X是不中断的极小过程，Pminij（t）是其诚实且标准的转移函数，由［1］可得E的Ray－Knight紧化珔E及ER，E+.由Ray－Knight方法我们可得珔E=E∪{∞}，其中{∞}中的点的个数唯一，且ER=E+=E.

（2）最小Q－过程X的Martin流出边界.X是不中断的极小过程，XT={Xτn}为X的嵌入链，τn表示X的第n个跳跃时刻，令Ω.由［2］可得XT的Martin边界E、本质Martin边界B、Martin核K（·，ξ）以及终极状态Xβ.易得最小Q－过程X的Martin流出边界Be、Martin消极边界Bp.从而在最小Q－过程不中断条件下有结论:X∞∈Bp，BeE=.

例 1 设E={1，2，3，4，…}E1={1，4，7，10，…}，E2={2，5，8，11，…}，E3={3，6，9，12，…}，转移函数PIJ（t）所确定的Q矩阵为

设X={Xt}是上述Q矩阵对应的Q过程，XT={Xτn}为X的嵌入链，则XT以Π=（Πij）i，j∈E为单步转移概率.这时{Xt}的轨道为下面三种情形:

且Kλ（2，ξ1）=Kλ（3，ξ1）=Kλ（5，ξ1）=…=0，故ξ1Be且 ξ1∈Bp，同理 ξ2Be且 ξ2∈Bp，ξ3Be且ξ3∈Bp，即最小Q－过程X的本质Martin边界B={ξ1，ξ2，ξ3}，Martin 流出边界Be=Φ ，Martin 消极边界Bp={ξ1，ξ2，ξ3}.

注:该例说明一般情况下，Pminij（t）诚实时最小Q－过程的Martin流出边界点要比R－K紧化所加边界点要多;但如果Q单流出，则两种情况所加边界点个数相同.

2 最小Q－过程的Martin流入边界与Ray－Knight紧化

由［3］若E+E有限，则存在双射:^Be→E+E.下面举例详细说明Martin流入边界^Be与 Ray－Knight紧化之间的一一对应关系，该例有助于研究马氏链构造论中边界点的构造.

例2 设E={1，2，3，4，…}，E1={1，4，7，10，…}，E2={2，5，8，11，…}，E3={3，6，9，12，…}，设q=0，1i3;qi=i2，i4，i∈E.令qij=－qi，若i=j;qij=－qi，若i=j+3;qij=0，其它.设X={X（t）}是上述Q=（qij）矩阵对应的极小过程，则{X（t）}的轨道为:

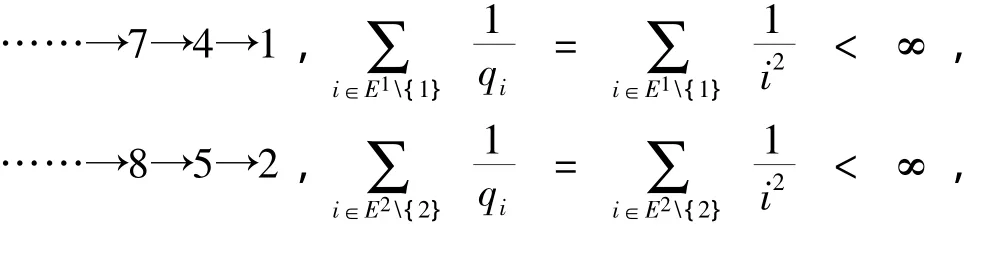
［1］Yang，X.Q.，The Construction Theory oI Denumerable Markov Processes［M］.Hunan Science and technology Publishing House，1990.

［2］Getoor，R，K.，Markov Processes:Ray Processes and Right Processes［M］.Springer－ Verl－ ag，Berlin Heidelberg New York，1975.

［3］徐长伟，阎国军，郝淑双.最小Q－过程的Martin流入边界与 Ray－Knight紧化［J］.应用概率统计，2011（6）.

［4］王梓坤，杨向群.生灭过程和马尔科夫链［M］.北京:科学出版社，2005.

O211.62

A

1008－7974（2014）03－0028－03

2014－02－12

郝淑双（1978－），女，河南南阳人，硕士，讲师.

河南省教育厅科学技术研究项目（编号:2012B110016）.

（责任编辑:王宏志）