Pt纳米颗粒几何特征与结构稳定性的原子尺度研究

胡红远, 邓 磊, 陈方来, 魏小平, 戴 震, 汤剑锋



Pt纳米颗粒几何特征与结构稳定性的原子尺度研究

胡红远, 邓 磊, 陈方来, 魏小平, 戴 震, 汤剑锋*

(湖南农业大学 理学院, 湖南 长沙, 410128)

基于金属纳米颗粒的几何特征及其幻数结构构建了一系列不同粒径和形貌的Pt纳米颗粒, 利用改进分析型嵌入原子势与淬火分子动力学模拟研究了其结构稳定性. 一方面揭示了各表面位比例、比表面积、平均配位数与粒径、形貌的定量关系; 另一方面预测了晶体结构Pt纳米颗粒的平均原子结合能与颗粒尺寸的线性关联; 二十面体形貌具有最密排的表面, 尺寸较小时表面能的贡献使之成为首选结构, 但大尺寸时应变能使之最不稳定; 由于应变能的释放, 晶态截切多面体小颗粒的稳定性与二十面体相仿, 尺寸增大时具有最高稳定性.

纳米催化剂; 几何特征; 结构稳定性; 分子动力学模拟

贵金属纳米材料具备独特的催化性能, 在石油化工、清洁能源、环境保护等领域有着广泛的应用价值和前景. 近年来, 以氢、乙醇、甲酸和甲醇等为代表的可再生、清洁能源的开发和利用越来越受到关注. 铂基催化剂在促进这些燃料常温下高效转化的电催化反应中表现出极其优异的性能[1—3]. 目前对铂基催化剂的研究主要集中在提高贵金属铂的使用效率上, 通常可通过两种途径来实现: 一是增大其比表面积, 相应显著提高其质量活性, 如制备粒径更小或者具有多孔结构的纳米催化剂; 二是调控催化剂的表面几何或电子结构以达到调控其催化活性的目的, 如掺杂非贵金属形成核壳结构, 通过形貌控制使得纳米催化剂暴露不同种类、比例的表面活性位等. 近年来, 关于铂基纳米结构催化剂的制备、表征、表面结构调控的研究工作取得了一系列成果[1—5], 为贵金属纳米材料在催化相关领域的应用奠定了坚实的基础.

研究表明, 纳米结构催化剂的催化性能与其晶体结构密切相关[1—4]. 首先, 一定形貌的纳米颗粒具有多种不饱和表面原子, 这些表面位通常表现出不同的催化活性. 同时, 颗粒尺寸或形状的变化也会导致表面活性位的比例或种类随之变化, 进一步改变纳米催化剂活性或选择性. 此外, 负载型纳米颗粒的粒径(或纳米多孔贵金属的孔径)越小则比表面积越高, 从热力学角度而言则越不稳定, 纳米颗粒自发团聚、粗化和烧结, 致使催化性能衰减[1—4]. 热力学上, 纳米颗粒的结构稳定性是表面能、应变能、结合能等竞争与平衡的结果, 其中前两项与颗粒形状、尺寸密切相关. 可见, 从原子尺度理解纳米结构模型催化剂的表面活性位分布特征与本征热力学稳定性及其影响因素是纳米结构催化剂研究的基本问题之一.

负载型催化剂中活性组分为分散的金属或合金纳米颗粒, 所以形貌规整的清洁纳米颗粒自然成为研究纳米催化剂的理想模型. 多种本征或外界因素的影响使得模型催化剂的制备、表征颇具挑战性, 从机理上揭示催化剂的“结构-性能”关系对于实验研究而言将是繁琐而艰巨的任务, 而利用计算模拟从原子尺度研究模型纳米催化剂已成为十分活跃的前沿研究领域[3—5]. 本文构建了一系列具有典型形貌的Pt纳米颗粒作为模型催化剂, 分析了颗粒尺寸和形貌因素对表面活性位的影响, 利用改进分析型嵌入原子势和淬火分子动力学模拟方法获得了纳米颗粒的稳定/亚稳结构, 研究了不同尺寸、形貌下Pt颗粒的热力学稳定性, 揭示了其中表面能与应变能的竞争或协同性作用.

1 模型与方法

原子间相互作用势是所有原子模拟方法的基础, 其精确度和复杂度直接影响模拟结果的准确性和所需计算资源. 原则上, 基于密度泛函理论(DFT)的赝势具有较高的精度, 但受限于目前的计算能力, DFT方法应用于包含上万原子数的纳米颗粒存在困难. 本文采用改进的分析型嵌入原子(MAEAM)多体势来描述金属原子间的相互作用, 该形式的势函数已成功应用于研究块体材料、表面和纳米材料[6—8]. Pt的MAEAM势参数可参考文献[7].

基于大量实验和模拟结果, 构建了一系列具有典型形貌和幻数尺寸的纳米颗粒作为模型纳米催化剂[3—5]. 所有的纳米颗粒都通过淬火分子动力学方法弛豫到局域能量最小态.初始温度设置为300 K, 目标温度为1 K. 初始速度由麦克斯韦-玻尔兹曼分布给出, 如果某个原子的力分量与速度分量方向相反则将其速度设置为0, 反复多次直到体系总能快速达到局域最小. 图1给出了几种幻数尺寸、典型形貌纳米颗粒的原子堆垛模型: FCC结构的晶态纳米颗粒, 如八面体(OCT), 立方八面体(CUB), 截角八面体(TOC)结构; 具有20个密排(111)面的Mackay二十面体(ICO)准晶结构; 五次对称的十面体(DEC), 根据Ino和Marks提出的方案进行截切的变体十面体(IDEC和MDEC).可见, 具有同一幻数的纳米颗粒可能存在多种同质异构体, 如ICO, CUB和IDEC颗粒.

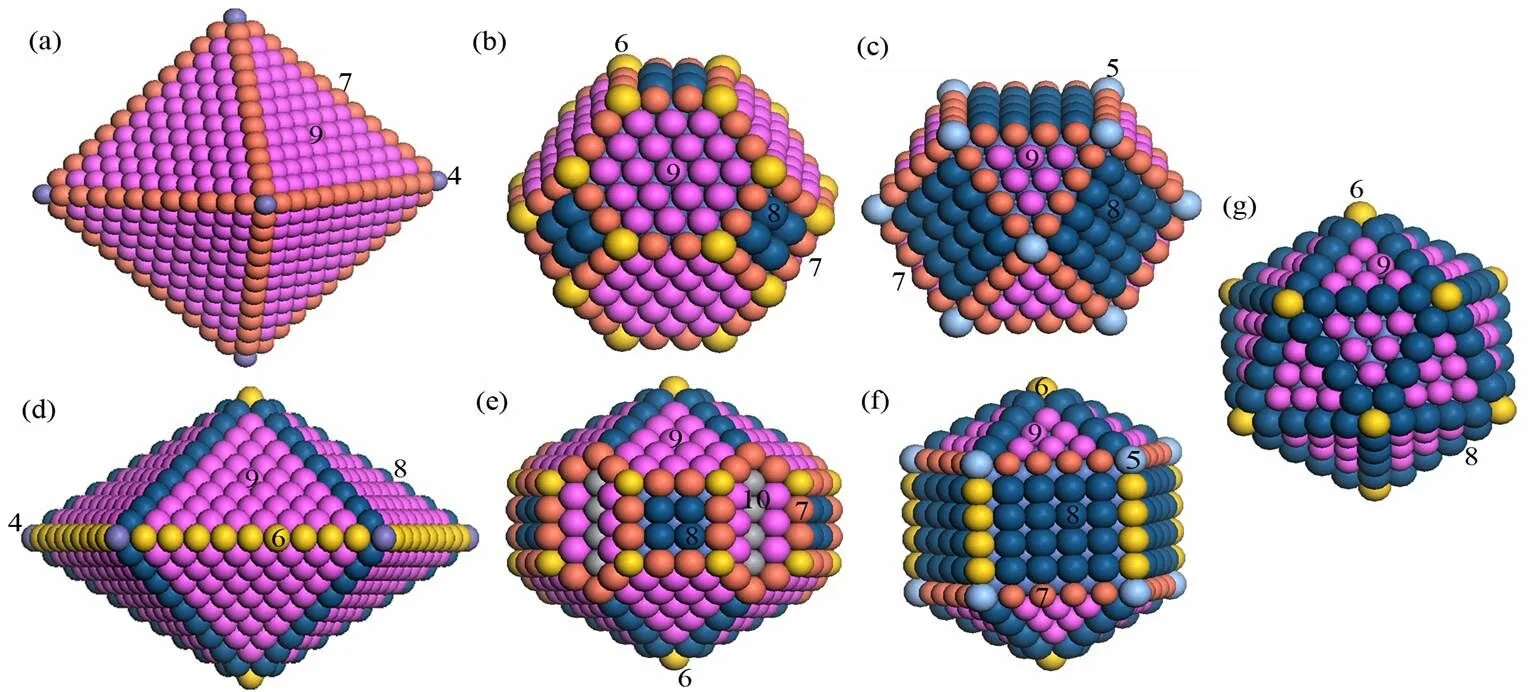
图1 几种幻数尺寸纳米颗粒的原子堆垛模型. (a) OCT; (b) TOC; (c) CUB; (d) DEC; (e) MDEC; (f) IDEC; (g) ICO,图中原子局域配位环境用颜色或数字标识

2 结果与讨论

2.1 几何特征与颗粒形貌及尺寸的关系

催化剂性能与其表面结构密切相关, 因而厘清纳米颗粒表面结构与颗粒形貌、尺寸的关系对于理解纳米催化剂的“结构-性能”关系至关重要. 基于图1的原子模型和不同位置的配位数, 可得到图2所示比表面积(S/)和平均配位数(C)随尺寸()与形貌的变化关系. 可见, 比表面积随颗粒尺寸增加而减小, 这将导致颗粒尺寸越大则越稳定. 对相似尺寸纳米颗粒而言, 比表面积以下述顺序依次增加IDEC = CUB = ICO＜TOC≈MDEC＜OCT＜DEC.本文基于理想颗粒模型得到的平均配位数与EXAFS的实验测量结果一致, 是反映纳米颗粒尺寸与形貌的重要参数[9]. 图2意味着颗粒尺寸增加则其平均配位数也增加, 并趋近于面心立方块体单晶. 在相当大的尺寸范围内, 平均配位数与形貌的定性关系为DEC＜CUB＜OCT≈IDEC＜TOC＜MDEC＜ICO.

图2 比表面积、平均配位数与颗粒形貌、尺寸的定量关系

为进一步阐明平均配位数随形貌变化趋势的根源, 图3给出了不同表面位对总表面原子的贡献随颗粒尺寸、形貌的变化. 图3表明, 对于各种形貌, 以下一般规律都成立: 由于顶位原子总数与颗粒形貌有关而与尺寸无关(为常数), 从而顶位原子比例随颗粒尺寸的增加而快速减小; 棱边原子与定位原子类似, 但下降趋势变缓; 有趣的是, 平整面比例随颗粒尺寸增加反而提高, 其中MDEC颗粒的(100)面比例与其截切方式有关.

由于各表面位的种类和比例都与颗粒形貌相关, 所以ICO、DEC和OCT颗粒表面(111)面占优, IDEC和CUB颗粒表面则为(100)面主导, MDEC和TOC颗粒表面由(100)面和(111)面共同占优.对于不同形貌的颗粒, 还需考虑棱边原子对表面的贡献(尤其是颗粒尺寸较小时), 它与平整面原子的贡献在不同尺寸区间内存在竞争. 通常认为, 这些配位数较低的表面原子是很多结构敏感反应的活性位[10]. 根据图3的结果, 处于不同位置的表面原子配位数不同, 且随颗粒尺寸和形貌变化, 因此, 催化剂尺寸和形貌将极大地影响结构敏感反应的活性和选择性.

图3 各表面位与总表面原子之比与颗粒形貌、尺寸的定量关系

2.2 结构稳定性

纳米颗粒的稳定性是表面能, 弹性应变能与界面能3者竞争与平衡的结果. 通常, 界面能贡献较小, 则纳米颗粒总能可用下式近似描述[3, 11—12]:

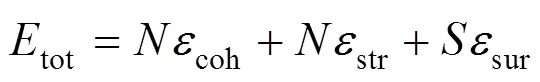
式(1)中,coh和str是单个原子结合能和应变能对总能的贡献,sur是单位表面积贡献的表面能. 其中, 纳米颗粒的表面积可通过下列近似获得:

式(2)中是几何因子, 不同形貌则不同. 将式(2)代入式(1)可得:

对于晶体结构纳米颗粒, 应变能可视为0, 有:

式(4)中为颗粒内部原子的能量贡献, 近似等于理想晶体的结合能(即颗粒尺寸趋近无穷大时退化为宏观晶体). 由于ICO和DEC等非晶体结构存在内部应变, 式(4)的线性关系不再成立. 在这种情况下, 用每表面原子的平均过剩能来表征纳米颗粒的稳定性:

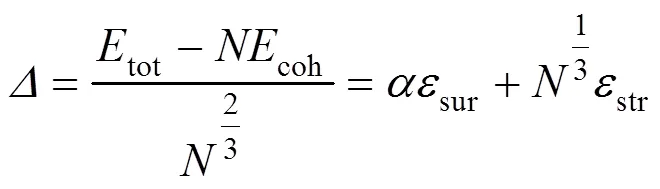
DEC和OCT颗粒表面几乎全为(111)面原子, 具有最低表面能, 但其形状与Wulff构造偏差较大, 存在大量低配位的顶位和棱边原子, 不如其它结构稳定, 下文将不再考虑这两种形貌. 图4给出了Pt纳米颗粒中平均原子能量随颗粒尺寸(以原子总数立方根的倒数表征)的变化, 其中实心符号为模拟结果, 实线为式(4)的拟合结果. 可见, 颗粒尺寸越大则平均原子能量越低, 越稳定. 在较大的尺寸范围内, TOC结构能量最低, MDEC结构与之接近; 具有相同幻数的ICO、IDEC和CUB颗粒能量较高, 其中IDEC与CUB两者几乎一致, 在大于500原子的尺寸范围内稳定性均高于ICO. 事实上, 不同尺寸和形状的纳米颗粒的稳定性取决于式(1)中所示几种能量的贡献与竞争. 对晶体结构的TOC和CUB纳米颗粒, 线性关系成立, 拟合参数为a = -5.842 eV(宏观晶体为-5.840 eV), 说明颗粒内部原子与宏观晶体原子能量上没有差别. 式(4)还可得到表面原子的贡献: 对于CUB颗粒, 其参数b = 3.675 eV; 而对于TOC颗粒, b = 3.279 eV. 由此可见, CUB颗粒的能量稳定性低于TOC结构, 源于其较高的表面能.对于IDEC、ICO和MDEC结构而言, 其内部应变的存在使得参数a、b不能精确描述式(1)中各能量项的贡献, 需引入式(5)定义的过剩能进行合理描述.

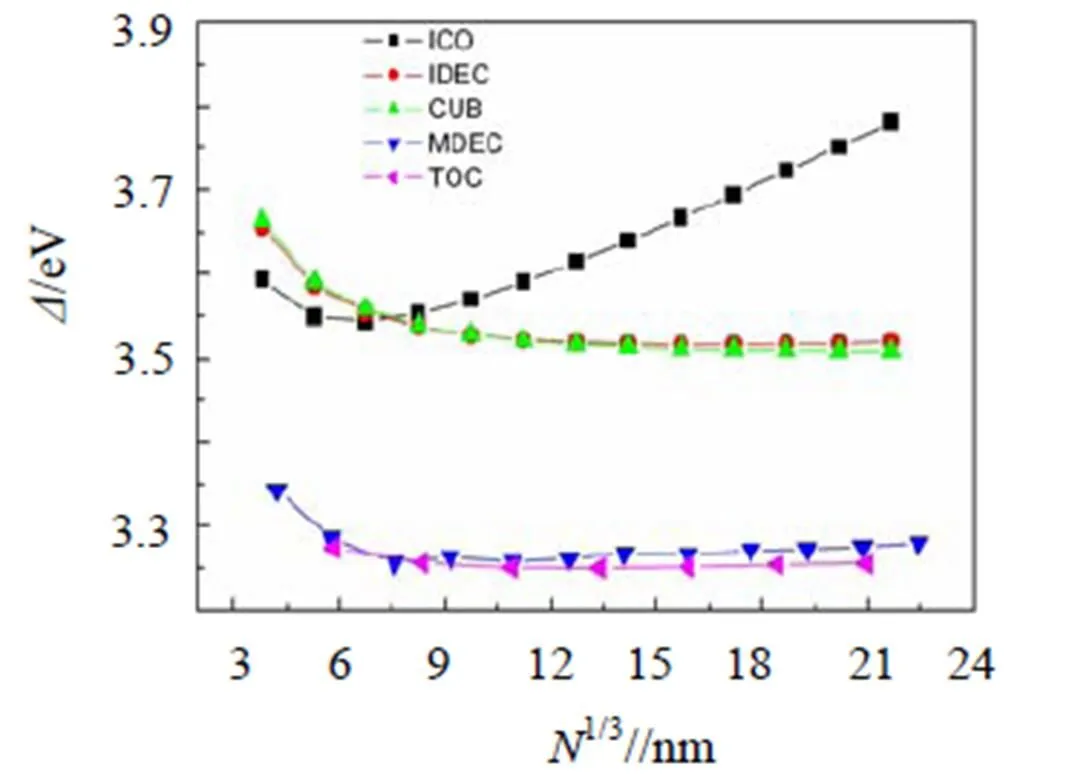
图5 表面原子过剩能Δ与颗粒尺寸的定量关系

图5给出了每表面原子的过剩能与颗粒尺寸的定量关系.对于MDEC、IDEC和ICO等结构, 式(5)中的应变能项都有贡献, 对大尺寸CUB和TOC结构颗粒无贡献. 因而, 随着尺寸的增加, ICO颗粒的过剩能先是迅速减小至最小, 然后快速增加; CUB和TOC颗粒的过剩能逐渐减小并趋于常数; MDEC和IDEC颗粒在大尺寸时对应斜率为略大于0的直线. 但对于各种形貌的小尺寸颗粒, 由于包含的原子数较少, 式(2)的近似不再合理, 导致式(5)部分失效[3].

既然核内原子结合能与具体形貌无关, 均接近块体原子的结合能, 纳米颗粒的能量稳定性可仅考虑表面能与应变能的竞争. 首先, 可通过尽量提高密排面比例或减小表面积来实现表面能的最小化. 基于这种考量, 小尺寸颗粒的最稳定形貌将是ICO, 因为它不仅具有最小的表面积, 而且表面由20个(111)面构成. 另一方面, 20个完美四面体不能堆砌出一个完整的ICO形貌, 意味着需通过弛豫变形让这些四面体共享顶点和界面形成完整的ICO. 这种堆垛致使ICO内部存在应变, 而且整体应变能随颗粒尺寸的增加剧烈增加, 使其结构稳定性越来越低[11]. OCT和DEC表面虽然也由(111)面构成, 但表面能和总表面积不够小, 因而结构稳定性较差. 经过合理截切从而暴露出(100)面的IDEC和CUB具有跟ICO相同的表面积, 但稳定性稍逊于ICO结构.通过继续截切得到的MDEC和TOC不仅暴露的(100)面比例降低, 并且截切和表面弛豫均可大大释放应变能, 因而在小尺寸时具有与ICO差不多的稳定性, 尺寸较大时具有最好的稳定性. 虽然还存在其他截切方式[3], 本文考虑的典型形貌的结论可作为预测不同形貌颗粒能量稳定性及其尺寸范围的简单、有效判据.

应该指出, 纳米颗粒聚集、烧结、长大等现象的主要驱动力是其高比表面积引起的高过剩能[3, 13]. 实验上通常用高分子、嵌段共聚物、树枝状聚合物或有机配体来稳定这类高比表面积纳米材料. 当外界条件发生较大变化时(如煅烧掉这些保护、稳化成分), 纳米结构材料就会自发聚集成团(颗粒)或粗化(颗粒及纳米多孔材料)以降低表面能. 另一方面, 注意到相近尺寸、不同形貌的纳米颗粒之间能量相差无几, 这意味着只需少量的动能就能驱动颗粒间发生结构相变.从热力学角度而言, 实验上制备的纳米颗粒为何通常具备多种形貌并存在较宽的尺寸或孔径分布就不难理解了. 由于纳米颗粒包含原子数不多, 从动力学角度而言各种形貌之间也很易发生结构相变.分子动力学模拟结果表明, 即便初始条件相同, 液态金纳米颗粒经冷却可得到形貌不同的固体纳米颗粒, 其中大部分具有ICO结构, 少量为不完全截切的DEC、孪生TOC和密排六方结构[14].

3 结语

基于金属纳米颗粒的几种典型形貌构建了一系列不同幻数尺寸的Pt纳米颗粒作为模型纳米催化剂, 利用改进分析型嵌入原子势和淬火分子动力学模拟方法获得了纳米颗粒的稳态/亚稳态结构, 分析了纳米催化剂的几何结构特征, 揭示了比表面积、平均配位数、各表面位比例与颗粒尺寸、形貌的定量关系, 研究了不同尺寸、形貌下Pt颗粒的热力学稳定性, 揭示了其中表面能与应变能的竞争性或协同性作用. 对于晶体结构Pt纳米颗粒, 其平均原子结合能与颗粒尺寸存在线性关联, 说明颗粒内部原子与宏观完整晶体原子本质上没有差别.过剩能分析指出: 二十面体形貌具有最密排的表面, 尺寸较小时表面能的贡献使之成为首选结构, 但大尺寸颗粒内部的巨大应变能使之最不稳定; 由于应变能的释放, 合理截切的八面体或十面体小颗粒具有接近二十面体的稳定性, 尺寸增大时具有最高稳定性. 此外, 还指出纳米颗粒的高比表面积和不同形貌间的相似稳定性将导致纳米催化剂的自发聚集、粗化、烧结、相变, 从而催化性能衰减. 本文从原子尺度揭示了中大尺度纳米颗粒的几何结构特征与结构稳定性规律, 为设计稳定高效的纳米催化剂提供了新的思路.

[1] Chen A C, Holt-Hindle P. Platinum-based nanostructured materials: synthesis, properties, and applications[J]. Chem Rev, 2010, 110(6): 3767—3804.

[2] Tian N, Zhou Z Y, Sun S G, et al. Synthesis of tetrahexahedral platinum nanocrystals with high-index facets and high electro-oxidation activity[J]. Science, 2007, 316(5825): 732—735.

[3] Baletto F, Ferrando R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects[J]. Rev Mod Phys, 2005, 77(1): 371—423.

[4] Ferrando R, Jellinek J, Johnston R L. Nanoalloys: From theory to applications of alloy clusters and nanoparticles[J]. Chem Rev, 2008, 108(3): 845—910.

[5] 程道建. 新型双金属纳米簇催化剂结构和物性的分子模拟研究[D]. 北京: 北京化工大学, 2008: 10－13.

[6] 张邦维, 胡望宇, 舒小林. 嵌入原子方法理论及其在材料科学中的应用──原子尺度材料设计理论[M]. 长沙: 湖南大学出版社, 2003: 392－464.

[7] 张智. 金属纳米团簇的结构演变与熔化特性的原子模拟[D]. 长沙: 湖南大学, 2007: 37.

[8] 邓磊. Ag-Au-Pt合金纳米颗粒表面偏聚的原子模拟[D]. 长沙: 湖南大学, 2011: 44－79.

[9] Beale A M, Weckhuysen B M. EXAFS as a tool to interrogate the size and shape of mono and bimetallic catalyst nanoparticles[J]. Phys Chem Chem Phys, 2010, 12(21): 5562—5574.

[10] Koper M T M. Structure sensitivity and nanoscale effects in electrocatalysis[J]. Nanoscale, 2011, 3(5): 2054—2073.

[11] Cleveland C L, Landman U. The energetics and structure of nickel clusters: Size dependence[J]. J Chem Phys, 1991, 94(11): 7376—7396.

[12] Baletto F, Ferrando R, Fortunelli A, et al. Crossover among structural motifs in transition and noble-metal clusters[J]. J Chem Phys, 2002, 116(9): 3856—3863.

[13] José-Yacamán M, Gutierrez-Wing C, Miki M, et al. Surface diffusion and coalescence of mobile metal nanoparticles[J]. J Phys Chem B, 2005, 109(19): 9703—9711.

[14] Chushak Y G, Bartell L S. Melting and freezing of gold nanoclusters[J]. J Phys Chem B, 2001, 105(47): 11605—11614.

Atomistic study of geometric features and structural stability of Pt nanoparticles

HU HongYuan, DENG Lei, CHEN FangLai, WEI XiaoPing, DAI Zhen, TANG JianFeng

(College of Science, Hunan Agricultural University, Changsha 410128, China)

Based on the typical morphologies of metal nanoparticles(NP) and the magic numbers, a sierias of NPs were consturcted. The influence of particles’ sizes and morphologies on structural stability of Pt NPs have been investigated by using quench molecular dynamics simulations based on modified analytic embedded atom potentials. It is shown that average coordination number, surface-to-volume and site-to-surface ratio are all morphology- and size-dependent. Using energetic analyses as a guide, it is found that the average cohesive energy decreases linearly with the increasing particles’ sizes. As a result of the minimization of the strain energy and the surface energy, icosahedral NP is the most favorable morphology at small size but the least favorable one at large size. Better truncated decahedral or octahedral NPs are comparable with icosahedral at small sizes, and the most favorable at a range of particle sizes. These atomic-level understanding of the geometric features and structural stability of Pt NPs shed new light on the intelligently design of active and durable nanocatalysts.

nanocatalysts; geometric features; structural stability; molecular dynamics simulation

O 469

1672-6146(2014)01-0010-06

10.3969/j.issn.1672-6146.2014.01.004

通讯作者email: hnjftang@aliyun.com.

2013-11-28

湖南省大学生研究性学习和创新性实验计划项目(SCX1212); 湖南农业大学引进人才科学基金项目(12YJ04).

(责任编校:刘刚毅)