基于灰色模型和最小二乘支持向量机的卫星钟差预报

雷雨，赵丹宁

(1.中国科学院国家授时中心，陕西 西安 710600；2.中国科学院时间频率基准重点实验室，陕西 西安 710600；3.中国科学院精密导航定位与定时技术重点实验室，陕西 西安 710600；4.中国科学院大学，北京 100049)

基于灰色模型和最小二乘支持向量机的卫星钟差预报

雷雨1，2，4，赵丹宁1，3，4

(1.中国科学院国家授时中心，陕西 西安 710600；2.中国科学院时间频率基准重点实验室，陕西 西安 710600；3.中国科学院精密导航定位与定时技术重点实验室，陕西 西安 710600；4.中国科学院大学，北京 100049)

提出一种联合灰色模型(Grey Model，GM)和最小二乘支持机(Least-Squares Support Vector Machines，LS-SVM)回归算法的卫星钟差智能组合预报方法。首先根据历史钟差数据建立不同的GM(1，1)灰色模型，然后利用这些模型进行钟差预报，最后采用最小二乘支持向量机回归算法对不同GM(1，1)模型的预报结果进行非线性组合，以获得最终预报值。该方法在充分利用灰色模型所需原始数据少、建模简单等优点的基础上，结合最小二乘支持向量机所具有的小样本、非线性、泛化能力强等特性，提高了预报可靠性和精度。实例验证了该组合方法的可行性、有效性和实用性。

导航定位；卫星钟差；组合预报；灰色模型；最小二乘支持向量机

CN53－1189/P ISSN1672－7673

随着人们对卫星导航定位精度要求的提高，卫星钟差预报成为一项至关重要的工作。由于星载原子钟频率高且异常敏感，极易受到外界及其自身因素的影响，很难掌握其复杂细致的变化规律，因此建立精确的原子钟运行模型非常困难，相应地准确预报钟差也非常困难。为此发展了多种钟差预报模型，主要有二次多项式模型、灰色模型、时间序列模型、Kalman滤波、人工神经网络(Artificial Neural Network，ANN)等[1－5]。实际上，任何一种模型都存在一定的局限性，单一模型预报方法一般不可能在不同情况下都能获得令人满意的结果，也就是说在实际预报中单一模型方法具有较大的风险性。文[6]指出，一个变化异常复杂的非线性、非平稳随机序列很难使用单一的模型进行有效的预报。组合预报方法可以综合多种单一预报模型的优点，从而改善预报结果，降低预报风险[7]，所以为了提高卫星钟差预报的可靠性和精度，有必要在预报中研究和运用组合预报方法。

目前组合预报方法主要有两类:传统(线性)组合方法和智能(非线性)组合方法[7－10]。传统组合方法的典型代表有经典权法和最优权法，其中经典权法根据方差倒数定权，相比于最优权法具有较好的预报稳定性，是一种较成熟、常用的组合预报方法；传统组合方法物理意义明确，但权值的确定是一个难点，并且缺乏将各种方法进行非线性组合的能力。此外，这种组合方法是单一方法的凸组合，如果不满足这一条件，往往会带来较大误差。智能方法能非线性地拟合单一方法的预报结果，克服了传统组合模型中确定加权系数的困难。

智能算法包括人工神经网络和支持向量机(Support Vector Machines，SVM)等机器学习算法，相对于人工神经网络而言，支持向量机的泛化能力较强，并且较好地解决了小样本、非线性、高维数和局部极小点等实际问题[11]。因此，本文将支持向量机的一种改进算法——最小二乘支持向量机应用于卫星钟差的组合预报中，提出了一种基于灰色模型和最小二乘支持向量机回归算法的组合预报方法。实例验证了该方法的可行性和有效性。

1 灰色模型原理

GM(1，1)是最常用、最简单的一种灰色模型，下面介绍其建模过程。

设有原始钟差数据系列x(0)＝{x(0)(k)，k＝1，2，…，N}，与之对应的时间为tk(k＝1，2，…，N)。对x(0)进行一阶累加可得序列x(1)＝{x(1)(k)，k＝1，2，…，N}。

对于序列x(1)，其变化趋势可近似用如下的一阶线性微分方程进行描述:

式中，a称为灰系数，表示由模型计算得到的序列值的发展态势；u称为灰作用量，其大小反映序列的变化关系。

利用最小二乘法对参数a和u进行估计:

其中，

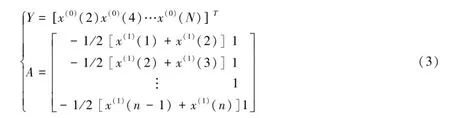
根据参数a和u的估计值，计算序列x(1)的预报序列:

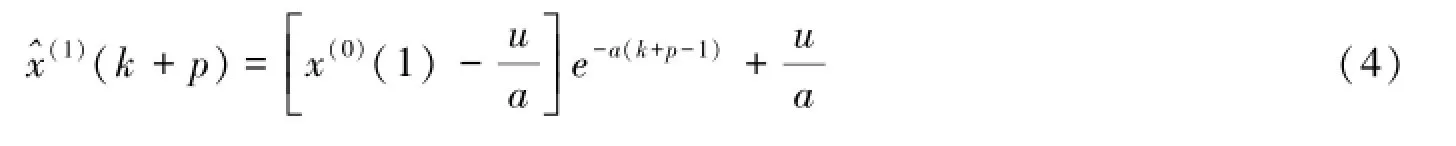
式中，p为预报点，p≥1。

2 最小二乘支持向量机回归算法

最小二乘支持向量机是在标准支持向量机基础上的扩展，它在保留支持向量机优秀特性的前提下，将支持向量机优化模型中的损失函数设定为最小二乘损失函数，并将不等式约束转化为等式约束，这样最小二乘支持向量机就将支持向量机的二次寻优问题转化成线性方程组的求解，极大地降低了求解的复杂性[12]，其回归算法如下。

式中，w为权值矢量；b为偏置。

标准支持向量机采用ε不敏感损失函数，最小二乘支持向量机选择误差ξi的二次项，优化问题为:

式中，ξi表示误差；C为容错惩罚因子。

根据约束非线性规划理论，求解上式可得方程组:

式中，lv＝[1，…，1]T；Ωij＝φT(xi)φ(xj)。采用最小二乘法求解上面的线性方程组即得到a和b。引入核函数K(x，xi)＝φT(x)φ(xi)，则最小二乘支持向量机回归模型为:

其中，核函数K(x，xi)为满足Mercer条件的任意对称函数，常用的核函数有径向基(Radial Basis Function，RBF)、线性和多项式函数，其表达式分别为:

式中，σ为核宽度。

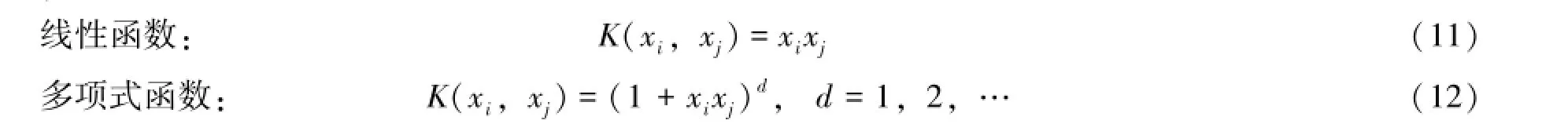
式中，d为多项式阶次。

与标准支持向量机相比，最小二乘支持向量机回归算法只需要确定核参数和惩罚因子，而不需要确定不敏感损失函数的值，这不仅简化了计算，也便于实际应用。

3 基于LS-SVM回归的灰色组合预报方法

单纯使用GM(1，1)模型进行卫星钟差预报，在实际应用中一般难以满足精度要求，而且模型的稳定性较差，预报风险较大；此外，采用多少个原始数据建模能达到较好的预报效果并没有明确的指导原则，具体地说，如果选取同一原始序列中的不同时间段、不同个数的历史数据进行建模，因其求解的灰系数和灰作用量不同，从而这些不同的GM(1，1)模型对同一时刻的预报值也就不同。为了降低预报风险，提高预报精度，可以综合这些GM(1，1)模型的预报结果。线性组合方法要求参与组合的各种方法的误差能保持稳定，否则会带来较大误差，并且无法有效处理综合建模过程中的非线性问题。故将最小二乘支持向量机和灰色模型结合起来，构建一种基于最小二乘支持向量机回归智能组合的卫星钟差预报方法，其建模过程如下。

设用m种不同序列长度的GM(1，1)模型作为基本预报模型，这m种模型在同一时刻t(t＝1，2，…，l)的预报值分别为xi1，xi2，…，xim，将这m个预报值作为最小二乘支持向量机的输入向量，该时刻的观测值作为输出值(目标值)，这样就可以构建由l个输入－输出样本对组成的训练集，利用此训练集对最小二乘支持向量机训练后，就可以对l＋1时刻的钟差值进行组合预报。基于最小二乘支持向量机回归的灰色组合预报原理如图1。

图1 基于LS-SVM和灰色模型的钟差预报模型Fig.1 Our model for predicting satellite clock errors which combines the LS-SVM and the Gray Model(GM)

4 算例分析

4.1 数据来源

从http://igscb.jpl.nasa.gov/components/prods.html网站下载了2010年12月12日和15日的国际GNSS服务(International GNSS Service，IGS)精密钟差数据，其采样间隔为5 min。考虑到目前在轨GPS卫星有30多颗，限于篇幅，从现有的5种类型卫星钟中各选1颗，它们分别是PRN02(IIR Rb)、PRN03(IIA Cs)、PRN04(IIA Rb)、PRN07(IIR-M Rb)和PRN25(IIF Rb)卫星。

4.2 建模方案

选取组合模型参数m＝3，即利用选定的原始数据对每个预报时刻建立3个灰色模型，分别记为GM-12、GM-18、GM-24，将其作为组合方法的基本模型，它们建模序列长度分别取为12个数据、18个数据和24个数据。

在采用最小二乘支持向量机进行预报时，模型参数、核函数及其参数和训练集对预报效果有重要影响。算例中分别选取径向基函数、线性函数和多项式函数作为核函数；采用网络搜索算法确定模型参数和核参数；选取训练集的样本个数l＝12，也就是说，利用最靠近待预报时刻的前12个时刻基本模型的预报值和实际值来构建训练样本集的输入向量和输出值，输入向量为3个灰色模型的预报值，并对训练集归一化处理，即变换到(－1，1)范围内。

4.3 结果分析

利用建立的组合预报模型进行6 h跨度的预报，为突出最小二乘支持向量机回归组合的优势，将其同常用的经典权方法进行比较，经典权法同样运用上述12个样本确定单一模型的权重系数。图2～6和表1分别给出了单纯灰色模型、经典权法和最小二乘支持向量机回归组合几种方法的预报残差序列和残差的统计特性(限于篇幅，表1只给出12日的预报结果)，其中MAX、MEAN分别代表最大误差和平均误差，RMS代表均方根误差。需要说明的是，径向基核函数和多项式核函数的预报误差非常大，因此选取线性核函数预报，下文结果都是基于该函数的结果。

图2 02号卫星钟差预报残差序列Fig.2 Errors of the predictions of the satellite clock errors in a time sequence for the No.2 satellite from various models.Our model is labeled as LS-SVM in the plots

图3 03号卫星钟差预报残差序列Fig.3 As Fig.2 but for the No.3 satellite

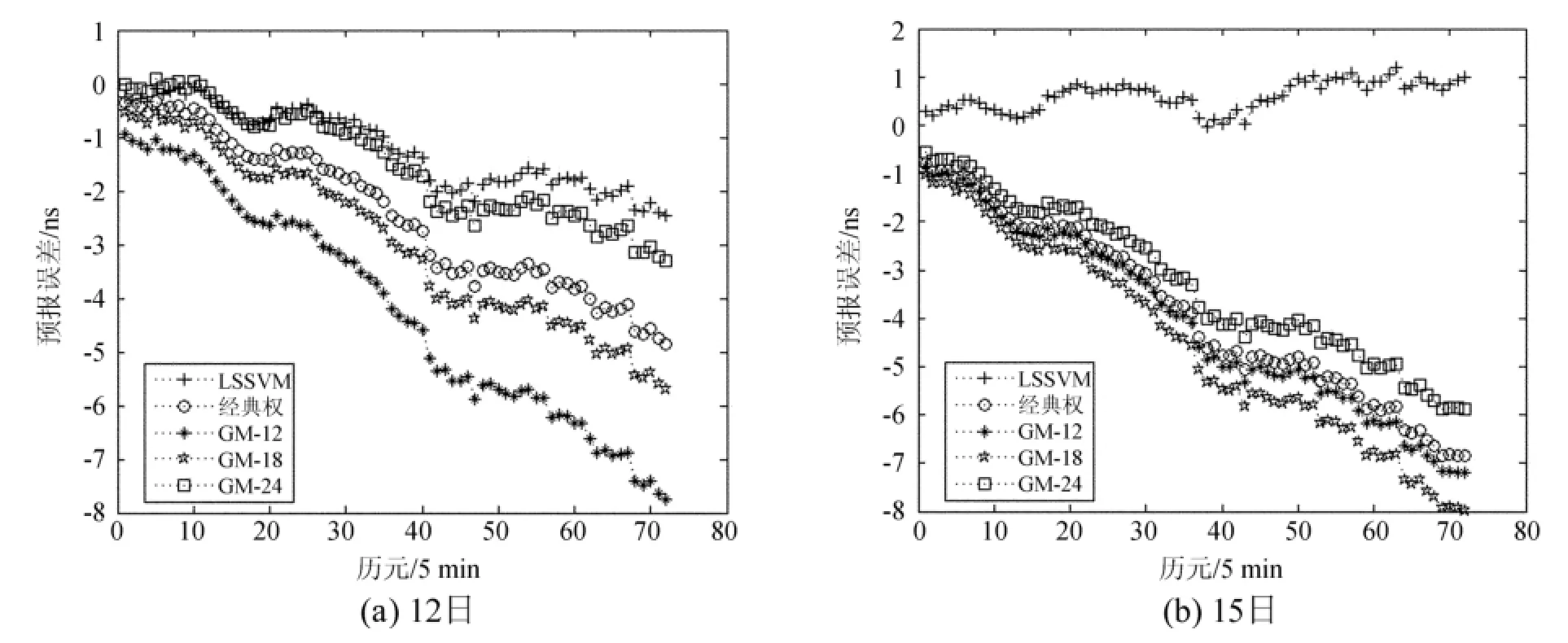
图4 04号卫星钟差预报残差序列Fig.4 As Fig.2 but for the No.4 satellite

图5 07号卫星钟差预报残差序列Fig.5 As Fig.2 but for the No.7 satellite

图6 25号卫星钟差预报残差序列Fig.6 As Fig.2 but for the No.25 satellite

结合图2～6，分析表1可以看出，最小二乘支持向量机回归组合预报的最大误差、平均误差和RMS均小于各种单一模型预报对应的误差，这说明组合预报的精度高于各种单一预报模型；此外，最小二乘支持向量机回归组合预报的各项误差也小于经典权对应的误差，验证了基于最小二乘支持向量机回归算法的组合预报思路的有效性，相比于所用的单一灰色模型和常用的经典权组合方法具有更好的预报效果。

5 结 论

(1)卫星钟差的组合预报方法能有效地综合单一模型的预报结果，使得综合后的结果继承了每种模型的优点，从而可以降低单一模型的预报风险，提高卫星钟差预报的可靠性。

(2)基于灰色模型和最小二乘支持向量机回归算法，提出了卫星钟差预报的非线性智能组合预报方法，该方法能最大程度利用已知信息，不仅避免了传统线性组合模型中权重系数确定复杂、困难的问题，实现了组合预报中所要求的非线性、变权值组合目标，而且降低了单一灰色模型的预报风险，改善了预报效果。

(3)最小二乘支持向量机回归性能与模型参数、核函数类型及其参数有较大关系，尤其参数选取对预报效果有较大影响，实际应用一般凭经验手工选取或搜索法选取，这会影响预报效率和预报效果，如何准确、快速地选择参数仍需进一步研究。

表1 残差序列的统计特性(单位:ns)Table 1 Statistics of the prediction errors shown in Fig.2 to Fig.6(—units:ns)

[1] 郑作亚，卢秀山.几种GPS卫星钟差预报方法比较及精度分析[J].山东科技大学(自然科学版)，2008，27(4):6－11＋15.

Zheng Zuoya，Lu Xiushan.Comparison and precision analysis of several GPS satellite clock bias prediction methods[J].Journal of Shandong University of Science and Technology(Natural Science)，2008，27(4):6－11＋15.

[2] 崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报(信息科学版)，2005，30(5):447－450.

Cui Xianqiang，Jiao Wenhai.Grey system model for the satellite clock error predicting[J].Editorial Board of Geomatics and Information Science of Wuhan University，2005，30(5):447－450.

[3] 徐君毅，曾安敏.ARIMA(0，2，q)模型在卫星钟差预报中的应用[J].大地测量与地球动力学，2009，29(5):116－120.

Xu Junyi，Zeng Anmin.Application of ARIMA(0，2，q)model to prediction of satellite clock error[J].Journal of Geodesy and Geodynamics，2009，29(5):116－120.

[4] 朱祥维，肖华，雍少为，等.卫星钟差预报的Kalman算法及其性能分析[J].宇航学报，2008，29(3):966－970＋1052.

Zhu Xiangwei，Xiao Hua，Yong Shaowei，et al.The Kalman algorithm used for satellite clock offset prediction and its performance analysis[J].Journal of Astronautics，2008，29(3):966－970＋1052.

[5] 郭承军，滕云龙.基于小波分析和神经网络的卫星钟差预报性能分析[J].天文学报，2010，51(4):395－403.

Guo Chengjun，Teng Yunlong.Performance analysis of satellite clock bias based on wavelet analysis and neural network[J].Acta Astronomica Sinica，2010，51(4):395－403.

[6] Huang N E，Wu M L，Qu W D，et al.Applications of hilbert-huang transform to non-stationary financial time series analysis[J].Applied Stochastic Models in Business and Industry，2003，19(3):245－268.

[7] 王继刚，胡永辉，何在民，等.组合模型预报导航卫星钟差[J].大地测量与地球动力学，2012，32(1):84－88.

Wang Jigang，Hu Yonghui，He Zaimin，et al.Combination models for navigation satellite clock prediction[J].Journal of Geodesy and Geodynamics，2012，32(1):84－88.

[8] 李林川，吕冬，武文杰.一种简化的电力系统负荷线性组合预测法[J].电网技术，2002，26(10):10－13.

Li Linchuan，Lv Dong，Wu Wenjie.A linear combination based simplified load forecasting method for power system[J].Power System Technology，2002，26(10):10－13.

[9] 谢开贵，李春燕，周家启.基于神经网络的负荷组合预测模型研究[J].中国电机工程学报，2002，22(7):85－89.

Xie Kaigui，Li Chunyan，Zhou Jiaqi.Research of the combination forecasting model for load based on artificial neural network[J].Proceedings of the CSEE，2002，22(7):85－89.

[10] 唐杰明，刘俊勇，杨可，等.基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J].电网技术，2009，33(3):63－68.

Tang Jieming，Liu Junyong，Yangke，et al.Short-term load combination forecasting by grey model and least square support vector machine[J].Power System Technology，2009，33(3):63－68.

[11] Vapnik V N.The nature of statistical learning theory[M].New York:Springer-Vertag，1995.

[12] Suykens J A K，Gestel T V，Brabanter J D，et al.Least squares support vector machines[M]. Singapore:World Scientific，2002.

Prediction of Satellite Clock Errors with a Combination of the Gray Model and the Least-Squares Support Vector Machines

Lei Yu1，2，4，Zhao Danning1，3，4
(1.National Time Service Center，Chinese Academy of Sciences，Xi′an 710600，China，Email:leiyu＠ntsc.ac.cn；2.Key Laboratory of Time and Frequency Primary Standards，Chinese Academy of Sciences，Xi′an 710600，China；3.Key Laboratory of Precision Navigation and Timing Technology，Chinese Academy of Sciences，Xi′an 710600，China；4.University of the Chinese Academy of Sciences，Beijing 100049，China)

We propose a new method for predicting satellite clock errors.The new method combines the Gray Model(GM)and the Least-Squares Support Vector Machines(LS-SVM)regression algorithm.The method first builds different GM(1，1)models based on observational data of satellite clock errors.Future satellite clock errors are predicted from these models.The LS-SVM regression algorithm is employed to combine the prediction results of the GM(1，1)models in a nonlinear manner.This method keeps the advantages of the GM(1，1)models such as relatively small amounts of required observational data and the simplicity in data modeling，and in the mean time，it has all the useful features of the LS-SVM，including relatively few samples to be used，nonlinearity，and easy generalization.Therefore，the method improves the reliability and accuracy of prediction results over previous methods.Our experimental results show that the new method is feasible，effective，and practical.

Navigation and positioning；Satellite clock error；Combination method for prediction；Gray Model；Least-Squares Support Vector Machines

P228.41

A

1672－7673(2014)01－0039－07

2013－01－07；修定日期:2013－01－24

雷 雨，男，研究实习员.研究方向:GNSS时间传递.Email:leiyu＠ntsc.ac.cn