改进的整合加和模型INFCIM及其应用于混合物毒性预测

覃礼堂,刘树深,莫凌云(1.桂林理工大学广西矿冶与环境科学实验中心,广西 桂林 541004；2.桂林理工大学环境科学与工程学院,广西 桂林 541004；3.同济大学环境科学与工程学院长江水环境教育部重点实验室, 上海 200092)

改进的整合加和模型INFCIM及其应用于混合物毒性预测

覃礼堂1,2,3,刘树深3*,莫凌云1,2(1.桂林理工大学广西矿冶与环境科学实验中心,广西 桂林 541004；2.桂林理工大学环境科学与工程学院,广西 桂林 541004；3.同济大学环境科学与工程学院长江水环境教育部重点实验室, 上海 200092)

目前,准确预测混合物毒性仍然面临着挑战, 为改进现有整合加和模型INFCIM,将该模型中“浓度=浓度+效应”形式修改为更加科学合理的“浓度=浓度+浓度”形式.利用分子电性距离矢量(MEDV)表征混合物组分的分子结构,以模糊数学中的隶属函数表征混合物组分的相似性和相异性,从而构建新的整合加和模型.利用6组六元混合物(共72个样本)验证模型的预测能力,结果表明,改进的模型能够准确预测无相互作用混合物毒性.在改进的模型中,利用多组混合物作为校正集,克服了INFCIM模型仅使用少量混合物数据作为校正集的缺点,使之更加可靠和具有代表性.

浓度加和；独立作用；化学混合物；农药

人类暴露于不同来源的大量化学品[1],通过实验测定化学混合物所有可能的组合是不实际和不可行的[2].数学模型在混合物毒性预测中起着重要的作用,浓度加和(CA)[3]和独立作用(IA)[4]是常用的2个参考模型.这2个模型利用混合物组分的浓度-响应信息,预测整体混合物毒性.然而,研究表明CA和IA模型有可能低估或高估混合物毒性[5].CA和IA模型仅适用于无相互作用混合物,对于具有相互作用(协同或拮抗)混合物,这2个模型的预测结果偏离了实际观测的浓度-效应数据.CA模型假设混合物组分具有完全相同的作用机理(MOA)或相同的作用位点,IA模型假设混合物组分具有完全不同的 MOA或不同的作用位点.实际环境混合物的各组分之间的相互作用复杂多样,一些组分可能具有相似 MOA,另一些组分则具有相异 MOA.应用单一的传统毒性评估模型如CA和IA只能评估相似MOA和相异MOA的特殊化学混合物.Cedergreen等[5]的研究结果表明,在158个二元化学混合物中,超过半数的化学混合物不能被CA和IA模型准确预测.2阶段预测(TSP)方法[6]只适合于混合物组分的 MOA明确已知的情况,而大多数化学品的MOA未知,也不可能将所有化学品分为相似和相异MOA[7].关于MOA仍然需要建立更加广泛和综合的分类方案[8].Qin等[9]利用多元线性回归方法,基于CA和IA模型建立了新的整合加和模型 ICIM,并利用多组混合物数据集加以验证模型的预测能力.Mwense等[10-11]提出一种混合物毒性预测方法,基于分子描述符和模糊集理论表征混合物组分的相似性和相异性,建立了整合模糊浓度加和-独立作用模型(INFCIM)用于评估混合物毒性.该方法首先利用模糊集理论的隶属函数表征混合物组分的相似性和相异性,将相似性和相异性系数分别乘以 CA和 IA模型,建立INFCIM 模型.然而,该模型是一个“浓度=浓度+效应”等式,这本身就相当武断,是不科学的.在这种情况下的相似性与相异性系数的物理意义及与结构相似性的关系是否真正存在的问题,就需要更深入的研究与更多更广泛的混合物实例加以证明.

为此,本研究目的是改进 INFCIM 模型为更加科学的形式:“总浓度=CA预测浓度+IA预测浓度”,利用改进后的模型,预测6种不同农药组成 6组六元混合物的毒性.此外,为了让模型具有真正的预测能力,利用均匀实验设计科学有效安排的混合物实验作为多个校正集,并应用等效应浓度比混合物来检验所建模型的预测能力.

1 材料与方法

1.1 数据集

利用 6组多元混合物的毒性数据[12]验证改进模型的预测能力.该数据集以 6个农药即敌敌畏、除草定、敌草快、环嗪酮、扑灭通和西草净等为混合物组分,共设计了4组六元均匀设计固定浓度比(UDCR)混合物和2组六元等效应固定浓度比(EECR)混合物射线[12].

1.2 分子结构表征

利用分子电性距离矢量(MEDV)方法[13-14]表征混合物组分的分子结构,获得每个化合物的MEDV分子结构描述符,并利用MEDV描述符计算混合物组分的相似性和相异性系数.

1.3 模糊集隶属函数

由于经典集合理论只能表示具有明确外延的概念,它不能表示模糊概念,也就是说元素要么属于或要么不属于一个集合.而模糊集合[15]可以定量地表征模糊概念和模糊现象,它把经典集合中的隶属关系加以扩充,使元素对集合的隶属程度由只能取0和1值推广到可以取0～1之间的任意一数值[10].

“相似”和“相异”概念描述混合物组分的MOA也是一个模糊概念,因此可用模糊隶属函数定量地表征混合物组分 MOA的相似性和相异性.目前化合物MOA缺乏的情况下,几乎不可能完全获得混合物组分的 MOA.因此,混合物组分 MOA的相似性和相异性可认为一个模糊概念,通过隶属函数表征混合物组分 MOA的相似性和相异性,相关隶属函数如下.高斯隶属函数:Z-隶属函数:

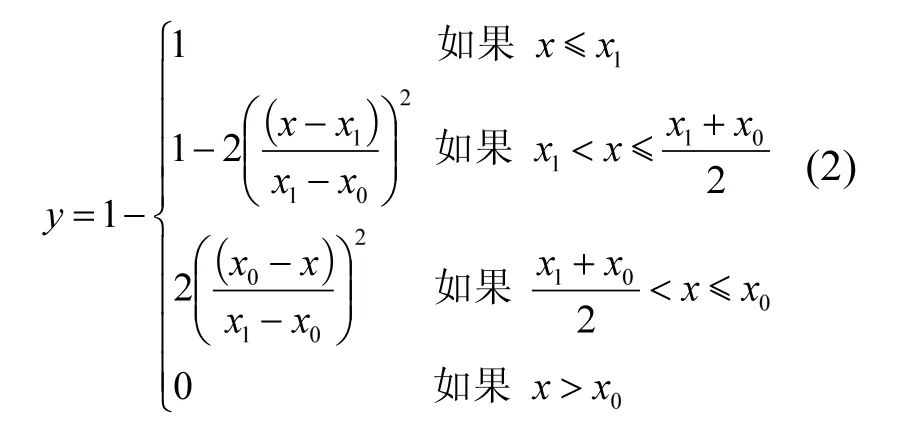
式中:y为隶属度,χ为分子之间距离,c为分子之间距离的平均值,σ为标准偏差,χ1和χ0为Z-隶属函数斜率的起点和终点.在混合物研究中,等式(1)的参数c和等式(2)的参数χ1设为0,表明两两分子之间距离为 0,分别对应相似性为 1和相异性为 0.因此,仅需要优化高斯函数的标准偏差σ和Z-隶属函数的参数χ0.

1.4 改进INFCIM模型

INFCIM数学表达式为:

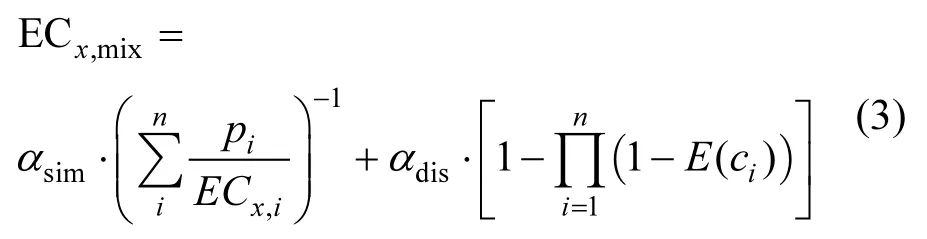
式中:ECχ,mix为混合物在 χ%效应下对应的浓度;αsim和αdis分别是相似性和相异性系数;pi为混合物组分的摩尔浓度比.ECχ,i为第i个组分在χ%效应下对应的浓度;E(ci)为第 i个组分在浓度 c下的效应.

从等式(3)可知,INFCIM 模型[10]的数学表达形式为“浓度=浓度+效应”,为此,提出更加合理的表达形式“浓度=浓度+浓度”.首先,通过二分法求得 IA模型预测的混合物浓度,从而替代等式(3)右边的第二项.二分法求得IA模型的预测浓度标记为ECχmix,IA,计算公式如下:

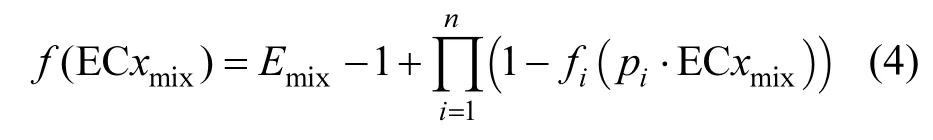
当 f(ECχmix)=0时,对应的 ECχmix即为 ECχmix,IA.式中:pi为第i个组分的浓度分数或相对浓度;Emix是混合物效应;fi为第 i个组分的浓度-响应曲线(CRC)拟合函数. 每个混合物的实验浓度记为 ECχmix,exp,利用CA模型预测混合物毒性的结果标记为ECχmix,CA,将整体相似性系数αsim和相异性系数αdis分别代入ECχmix,CA和ECχmix,IA项后得到改进的INFCIM模型如下:

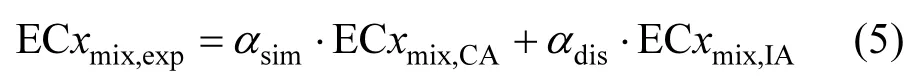
改进INFCIM模型的建模过程如下:

(1) 以非线性拟合函数Weibull模型[16]表征混合物组分及其混合物的CRC,获得非线性拟合函数的参数(α和β).

(2) 以 MEDV表征每个混合物组分的分子结构,获得MEDV描述子[17-18].

(3) 通过MEDV描述子,计算混合物中的两两组分之间距离(欧氏距离),欧氏距离公式如下:

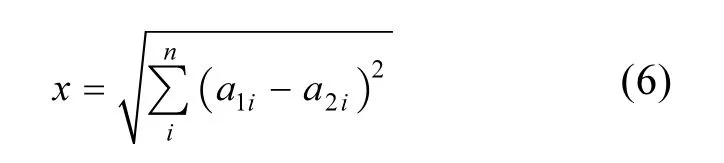
式中:χ为分子对之间距离;a1i和a2i分别2个化合物的第i个描述子.

(4) 使用混合物中的两两组分之间的欧式距离,通过模糊隶属函数表征混合物中两两组分之间的相似性和相异性,选择高斯隶属函数表征相似性,Z-隶属函数表征相异性.一个模糊集(矩阵)的相似性和相异性需要满足3个条件:自反性,对称性和传递性.一个矩阵通常满足自反性和对称性条件,而模糊传递条件不一定能满足.因此,需要计算模糊相似性和相异性矩阵的传递闭包.

(5) 使用CA和IA预测混合物毒性[16].利用第(1)步的单个物质和混合物的 CRC信息,通过CA模型预测混合物的效应浓度,其结果标记为ECχmiχ,CA.通过二分法求解等式(4),获得 IA模型预测的混合物效应浓度,结果标记为ECχmix,IA.

(6) 利用第 5步的计算结果,通过自举均值估计法,计算整个混合物的相似性和相异性,获得相似性系数αsim和相异性系数αdis,将αsim和αdis分别结合 CA和 IA模型计算的混合物效应浓度,建立混合物实验浓度 ECχmix,exp与 ECχmix,CA和ECχmix,IA的定量关系模型,即改进的 INFCIM 模型[式(5)].

(7) 利用改进的INFCIM模型预测混合物毒性.利用给定组分的混合物CRC信息来优化隶属函数参数,该参数可用于预测具有相同组分而不同组成的混合物.

2 结果与讨论

2.1 模型建立与验证

利用MEDV表征每个农药的分子结构,对于每个物质共计算得到原始91个MEDV描述子,去除数值为0的描述子,剩余 41个非零描述子.经验证,这41个非零MEDV描述子与6个农药的半数效应浓度的负对数(pEC50)的具有一定的正相关,其中MEDV的χ2描述子(MEDV第2个描述子)与6个化合物pEC50的相关性最高(等于0.8684).因此,使用41个非零MEDV描述子计算分子间的欧氏距离.

利用高斯隶属函数[式(1)]表征混合物组分的相似性,Z-隶属函数[式(2)]表征混合物组分的相异性,计算模糊相似性和相异性矩阵的传递闭包,利用自举均值估计法计算整个混合物的相似性系数αsim和相异性系数αdis,建立每组混合物的整合加和模型.以模型的计算值和实验值的均方根误差为目标函数,选择优化的隶属函数的参数,获得每组混合物的最佳 INFCIM 模型参数并列于表1.

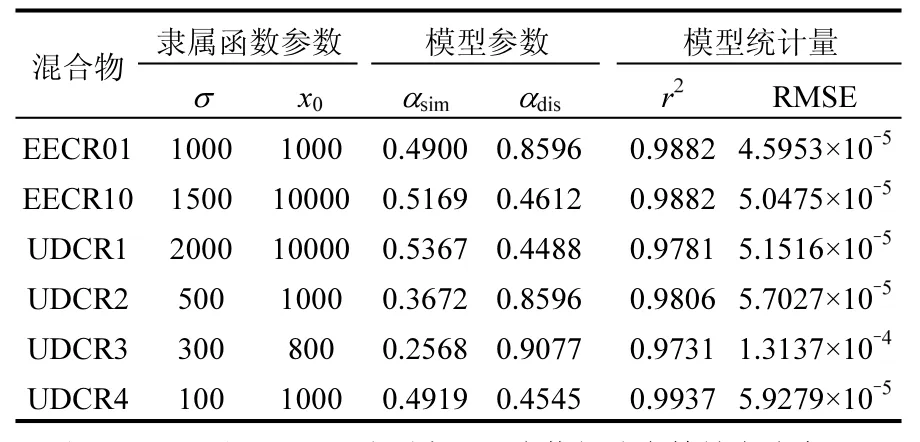
表1 改进INFCIM模型预测6组混合物毒性Table 1 Six mixture toxicities predicted by the improved INFCIM model

从表1可知,所有改进INFCIM模型的决定系数r2大于0.97,表明模型具有较好的估计能力.利用模型相似性系数αsim和相异性系数αdis带入等式(5),获得每组混合物的改进INFCIM模型.利用各自模型分别估计各自混合物的毒性,结果绘于图1.从图1可知,改进INFCIM模型能够准确评估6组混合物毒性.

以上所建立的模型是基于单个混合物的浓度-效应数据,因此每组混合物模型的相似性系数αsim和相异性系数αdis的数值不相等.该数据集共 6组六元混合物具有相同的组分和不同的浓度比例.理论上,相同的混合物组分应该具有相同的αsim和αdis数值.然而,以上的模型是经过优化而得到对应每组混合物的最优化模型.此外,一种化合物可能具有多种 MOA,相同化合物的不同浓度可能具有不同的 MOA[19].因此,以上获得每组混合物的αsim和αdis数值不相等,也是合理的.

为了使αsim和αdis代表整体混合物组分分子结构的相似性和相异性,也为了获得更加具有代表性的混合物模型.提出利用多组混合物的浓度-效应数据作为校正集模型,然后利用模型预测外部数据集.以 4组无毒性相互作用混合物UDCR1-UDCR4共48个样本建立模型,利用高斯隶属函数表征混合物组分的相似性,Z-隶属函数表征相异性,获得优化模型的数学表达式如下:

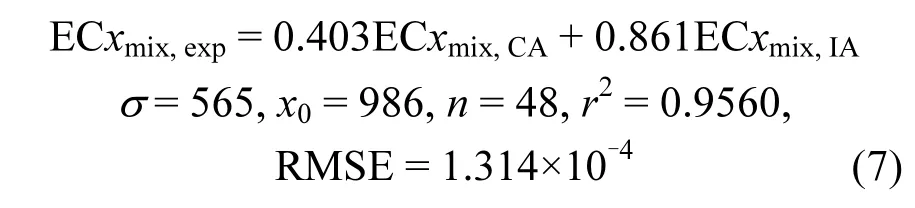
式中:σ和 χ0为隶属函数参数;n是模型包含样本数;r2为决定系数;RMSE估计均方根误差.

以上模型的r2为0.9560,表明模型具有较好的估计能力.利用无毒性相互作用的EECR01和EECR10混合物作用检验集,验证模型对外部样本的预测能力.检验集的相关系数r2test为0.9782,预测均方根误差(RMSP)为 6.5612×10-5,表明了所建立模型具有较好的外部预测能力,其预测混合物EECR01和EECR10的CRC绘于图2.

从图2可知,改进INFCIM模型的预测能力基本等同于CA模型和明显高于IA模型,表明了改进 INFCIM 模型能够准确预测无毒性相互作用混合物的毒性.

为了比较在不同效应水平(5%～90%)下改进INFCIM、CA和IA模型对EECR01和EECR10混合物的预测能力,通过效应残差比(ERR)法进行定量比较[20],ERR值越大表明误差越大.结果表明,IA模型在较低效应水平范围具有较高的ERR值.对于EECR01混合物,在5%～90%效应范围内,CA模型的ERR值为41.11%～6.02%,IA模型的 ERR值的范围为 166.30%～6.08%,改进INFCIM 模型的范围为-53.08%～1.86%.在低效应范围,改进 INFCIM 模型稍微过低估计EECR01混合物的毒性,CA模型稍微过高估计混合物毒性,而 IA模型明显过高估计混合物毒性.表明了CA和改进INFCIM模型的估计能力基本没有明显差别,而明显高于IA模型的估计能力.

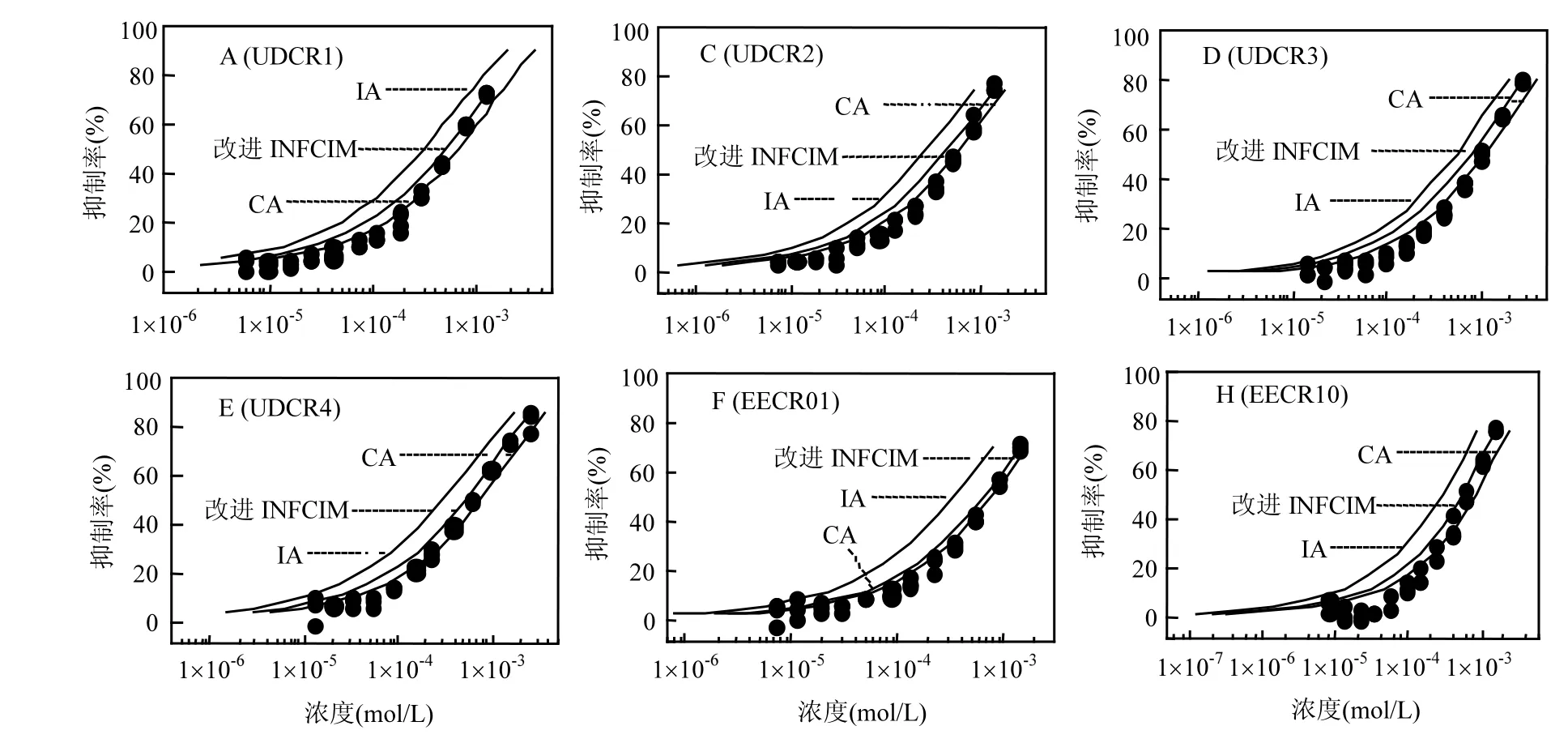
图1 改进INFCIM, CA和IA模型预测混合物毒性Fig.1 Mixture toxicities predicted by the improved INFCIM, CA, and IA models

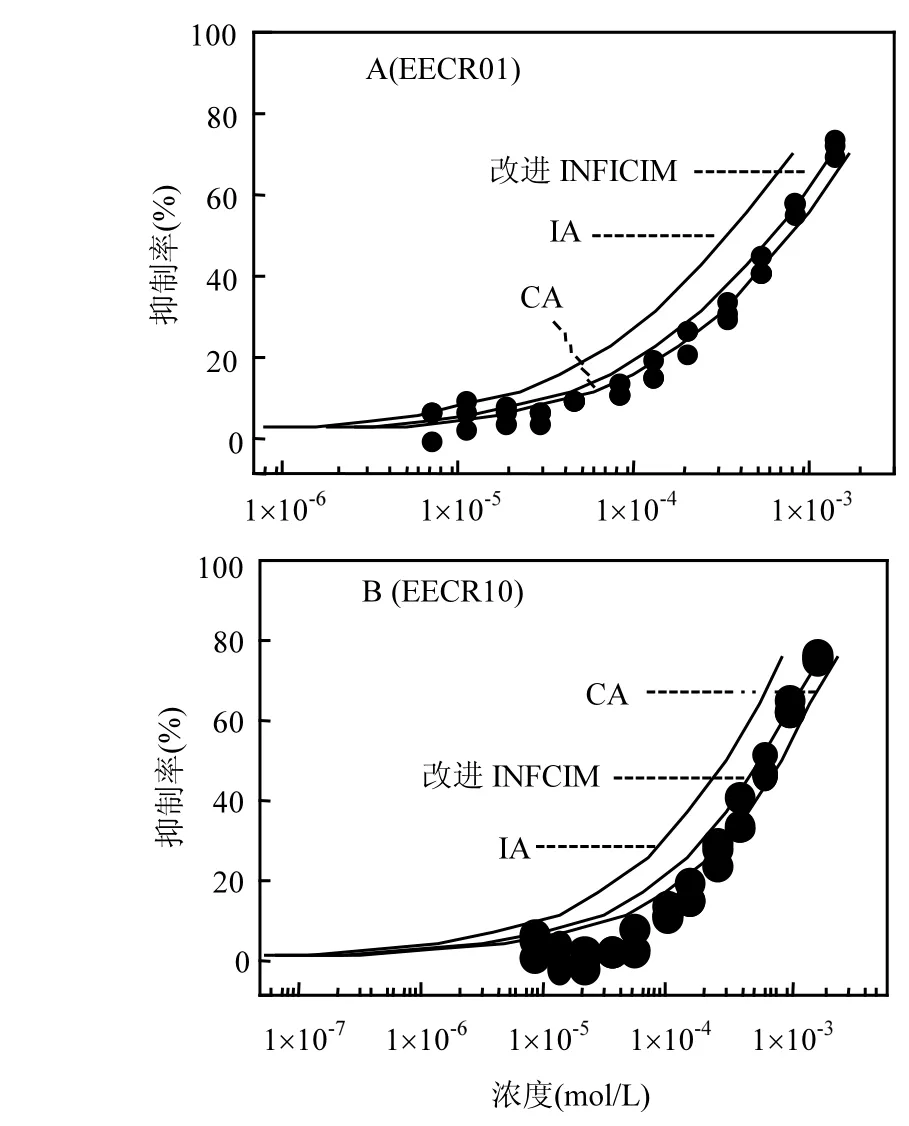
图2 改进INFCIM模型预测混合物毒性Fig.2 The improved INFCIM model for predicting mixture toxicity

对于EECR10混合物,在5%～90%效应范围内,CA模型的ERR值范围为98.42%～-3.76%,IA模型的 ERR值范围为 314.66%～8.31%,改进INFCIM 模型的范围为-88.69%～-1.28%.这表明了CA和改进INFCIM模型对EECR10混合物具有相近的估计能力,而明显高于IA模型的估计能力.因此,改进INFCIM模型与CA模型具有相近的预测能力和明显高于IA模型的估计能力.

通过以上分析可知,改进INFCIM模型对所有无相互作用混合物的毒性具有较好的预测能力,这不仅提供了混合物毒性评估新方法,而且为从混合物组分的分子结构解析混合物毒性提供可能的途径.

2.2 模型比较

为了比较改进 INFCIM 模型与其他模型的区别,将ICIM、改进INFCIM、INFCIM、CA和IA模型的相关信息列于表2.

首先,改进INFCIM与INFCIM模型的区别如下:(1)改进INFCIM模型的数学表达式形式为“浓度=浓度+浓度”,而INFCIM模型的数学表达式为“浓度=浓度+效应”.前者的数学等式更加合理;(2)改进INFCIM模型仅适用少量的描述子表征分子结构相似性,如6个农药体系中使用41个MEDV描述子,而INFCIM模型使用超过1000个描述子.后者使用的大量描述子并不都与混合物毒性相关;(3)改进INFCIM模型使用模型计算值和实验值的均方根误差为目标函数进行最小二乘优化,选择隶属函数参数,而INFCIM模型使用多目标优化技术选择隶属函数参数,前者计算更加直接;(4)改进INFCIM模型使用多个混合物浓度-效应数据作为输入数据,如4组UDCR混合物射线共48个样本作为输入数据,而INFCIM模型仅使用1组混合物数据的浓度-效应数据建模.前者的混合物浓度-效应数据更加具有代表性,保证了本文模型更加可靠.

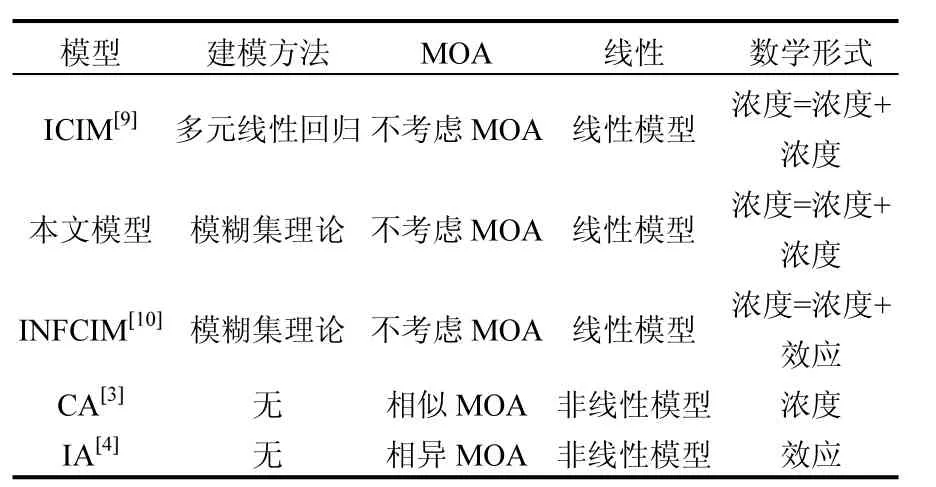
表2 不同混合物模型之间比较Table 2 Comparisons of different mixture models

其次,改进INFCIM与ICIM模型的建模方法不同.ICIM 模型是基于统计学中的多元线性回归方法建立模型,改进 INFCIM 模型是基于模糊集理论和混合物组分的分子结构,两个模型的建模方法有本质区别.改进INFCIM与INFCIM模型的建模方法一样,CA和IA不是整合模型而仅是一个数学表达式,因此CA和IA模型无建模方法.

再次,改进INFCIM模型与INFCIM和ICIM模型一样,不考虑混合物组分的作用模式(MOA),CA模型的假设是基于混合物组分具有完全相似 MOA,IA模型的基础假设是混合物组分具有完全相异的 MOA[21].改进 INFCIM、INFCIM、CA和IA模型仅适用于无毒性相互作用混合物.

最后,从模型的表达式可知,ICIM、改进INFCIM和INFCIM整合加和模型属于线性模型,而CA和IA模型是非线性数学表达式.CA模型计算得到的是混合物的效应浓度,IA模型计算混合物的效应.改进INFCIM与ICIM模型的数学表达形式为“浓度=浓度+浓度”,而INFCIM模型的数学表达形式为“浓度=浓度+效应”.改进INFCIM与ICIM模型的数学形式更加合理,更加科学,INFCIM 模型的数学形式的物理意义不够清晰.这是本文建立的改进INFCIM与INFCIM模型的主要区别之一.

2.3 讨论

该方法仍然需要进一步研究,比如:(1) 选择哪些描述符表征混合物组分的分子结构;(2) 相似性系数αsim和相异性系数αdis是否能够真正代表混合物组分的相似和相异性,则需要更多的实验加以验证;αsim和αdis与CA和IA模型之间,以及αsim和αdis与 MOA 之间是否存在一定的关系;(3) 如何从分子结构信息判定混合物毒性相互作用和毒性作用大小.(4)对于具有相互作用混合物,改进INFCIM是否能够准确预测,需要更多的实例和进一步深入研究.

3 结论

3.1 通过 6个农药混合物数据集验证了改进INFCIM 模型的评估和预测能力,结果表明对于无相互作用混合物,改进INFCIM模型不仅对内部建模混合物具有良好的估计能力,而且对外部混合物的毒性也具有良好的预测能力.此外,改进INFCIM 模型建立了混合物组分的分子结构与混合物毒性之间定量关系,这为从化合物分子结构解析混合物毒性提供了可行性.

3.2 改进INFCIM模型相比文献中的INCIM模型具有明显不同的特征.首先,改进INFCIM模型的数学表达式为“浓度=浓度+效应”形式,改进了文献中的INFCIM模型不合理的数学形式“浓度=浓度+浓度”.其次,改进 INFCIM模型应用具有充分代表性的UDCR混合物射线作为建立模型的校正集样本,因而充分考虑了混合物组分浓度发生变化时在不同混合物射线中产生效应的可能变化,保证了模型的稳定性和外推能力.

[1] Simmons J E. Chemical mixtures: Challenge for toxicology and risk assessment [J]. Toxicology, 1995,105(2/3):111-119.

[2] Martin H L, Svendsen C, Lister L J, et al. Measurement and modeling of the toxicity of binary mixtures in the nematode Caenorhabditis nlegans - a test of independent action [J].Environmental Toxicology and Chemistry, 2009,28(1):97-104.

[3] Loewe S, Muischnek H. Effect of combinations: Mathematical basis of problem [J]. Naunyn Schmiedebergs Arch. Exp. Pathol. Pharmakol., 1926,114:313-326.

[4] Bliss C I. The toxicity of poisons applied jointly [J]. Annals of Applied Biology, 1939,26(3):585-615.

[5] Cedergreen N, Christensen A M, Kamper A, et al. A review of independent action compared to concentration addition as reference models for mixtures of compounds with different molecular target sites [J]. Environmental Toxicology and Chemistry, 2008,27(7):1621-1632.

[6] Ra J S, Lee B C, Chang N I, et al. Estimating the combined toxicity by two-step prediction model on the complicated chemical mixtures from wastewater treatment plant effluents [J]. Environmental Toxicology and Chemistry, 2006,25(8):2107-2113.

[7] Syberg K, Jensen T S, Cedergreen N, et al. On the use of mixture toxicity assessment in REACH and the water framework directive: A review [J]. Human and Ecological Risk Assessment, 2009,15(6): 1257-1272.

[8] McCarty L S, Borgert C J. Review of the toxicity of chemical mixtures: Theory, policy, and regulatory practice [J]. Regulatory Toxicology and Pharmacology, 2006,45(2):119-143.

[9] Qin L T, Liu S S, Zhang J, et al. A novel model integrated concentration addition with independent action for the prediction of toxicity of multi-component mixture [J]. Toxicology, 2011, 280(3):164-172.

[10] Mwense M, Wang X Z, Buontempo F V, et al. Prediction of noninteractive mixture toxicity of organic compounds based on a fuzzy set method [J]. Journal of Chemical Information and Computer Sciences, 2004,44(5):1763-1773.

[11] Mwense M, Wang X Z, Buontempo F V, et al. QSAR approach for mixture toxicity prediction using independent latent descriptors and fuzzy membership functions [J]. SAR and QSAR in Environmental Research, 2006,17(1):53-73.

[12] Liu S S, Song X Q, Liu H L, et al. Combined photobacterium toxicity of herbicide mixtures containing one insecticide [J]. Chemosphere, 2009,75(3):381-388.

[13] Liu S S, Yin C S, Cai S X, et al. A novel MHDV descriptor for dipeptide QSAR studies [J]. Journal of The Chinese Chemical Society, 2001,48(2):253-260.

[14] Liu S S, Yin C S, Wang L S. Combined MEDV-GA-MLR method for QSAR of three panels of steroids, dipeptides, and COX-2inhibitors [J]. Journal of Chemical Information and Computer Sciences, 2002,42(3):749-756.

[15] Zadeh L A. Fuzzy sets [J]. Information and Control, 1965,8(3): 338-353.

[16] 刘树深,张 瑾,张亚辉,覃礼堂.APTox:化学混合物毒性评估与预测 [J]. 化学学报, 2012,70(14):1511-1571.

[17] Liu S S, Yin C S, Li Z L, et al. QSAR study of steroid benchmark and dipeptides based on MEDV-13 [J]. Journal of Chemical Information and Computer Sciences, 2001,41(2):321-329.

[18] Liu S S, Cao C Z, Li Z L. Approach to estimation and prediction for normal boiling point (NBP) of alkanes based on a novel molecular distance-edge (MDE) vector, lambda [J]. Journal of Chemical Information and Computer Sciences, 1998,38(3):387-394.

[19] Escher B I, Hermens J L M. Modes of action in ecotoxicology: Their role in body burdens, species sensitivity, QSARs, and mixture effects [J]. Environmental Science and Technology, 2002, 36(20):4201-4217.

[20] Wang L J, Liu S S, Zhang J, et al. A new effect residual ratio (ERR) method for the validation of the concentration addition and independent action models [J]. Environmental Science and Pollution Research, 2010,17(5):1080-1089.

[21] 刘树深,刘 玲,陈 浮.浓度加和模型在化学混合物毒性评估中的应用 [J]. 化学学报, 2013,71(10):1335-1340.

Improved integrated addition model INFCIM and its application on prediction of mixture toxicity

. QIN Li-tang1,2,3,

LIU Shu-shen3*, MO Ling-yun1,2(1.Guangxi Scientific Experiment Center of Mining, Metallurgy and Environment, Guilin University of Technology, Guilin 541004, China；2.College of Environmental Science and Engineering, Guilin University of Technology, Guilin 541004, China；3.Key Laboratory of Yangtze River Water Environment, Ministry of Education, College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China). China Environmental Science, 2014,34(7)：1890～1896

Recently, the accurately prediction of mixture toxicity remains a challenge. In order to modify the existed integrated addition model INFCIM (integrated fuzzy concentration addition-independent action model), the form of“concentration = concentration + effect” for the INFCIM model was modified into a reasonable form of “concentration = concentration + concentration”. The molecular electronegativity distance vector was used to characterize the molecular structures of mixture components. The fuzzy set theory was used to describe the degree of similarity and dissimilarity of mixture components. A new integrated addition model was then developed. Six mixtures (including 72 samples) with six components were used to test the predictive ability of the modified model. The results show that the modified model can accurately predict the non-interactive mixture toxicity. The proposed model based on the multiple mixtures overcomes the disadvantage of the model that only uses a single mixture data as calibration set. Thus, the modified model is more reliability and representativeness than the model based on a single mixture.

concentration addition；independent action；chemical mixture；pesticide

X503

A

1000-6923(2014)07-1890-07

覃礼堂(1982-),男,广西河池人,讲师,博士,主要从事环境毒理学研究.发表论文10余篇.

2013-09-25

国家自然科学基金资助项目(21177097,21207024);广西高校科学技术研究项目(ZD2014059);广西矿冶与环境科学实验中心资助项目(KH2012ZD004)

* 责任作者, 教授, ssliuhl@263.net