露天堆场防风抑尘网后湍流结构及抑尘效率的数值模拟

宋翀芳,彭 林,白慧玲,牟 玲,刘效峰 (太原理工大学环境科学与工程学院,山西 太原 030024)

露天堆场防风抑尘网后湍流结构及抑尘效率的数值模拟

宋翀芳,彭 林*,白慧玲,牟 玲,刘效峰 (太原理工大学环境科学与工程学院,山西 太原 030024)

建立了开放性露天堆场周围空气流动的三维数学物理模型,选择应用标准k-ε紊流模型进行了静态流场的数值模拟;分析了典型棱形堆迎风面、平顶面和背风面周围空气的湍流结构和表面受力特性;基于流场数据揭示了防风抑尘网不同孔隙率下空气动力学结构的分布规律.结果显示:物料堆平顶面剪切力随孔隙率增大而增大;料堆迎风面在孔隙率较小时出现局部涡流,表面剪切力方向向下,孔隙率较大时,网后空气垂直方向压差作用显著,表面剪切力方向向上;背风面始终处于回流区,表面剪切力和回流点数随孔隙率大小变化不显著.综合流场结构和受力分布可得最佳孔隙率为 0.2～0.4.该研究中对物料堆逐个表面进行空气动力学模拟可以避免由于剪切力方向不同产生矢量抵消而带来的计算失真.

露天堆场；数值模拟；湍流；抑尘网

露天堆场在外力作用下形成的颗粒扬尘污染已成为大气颗粒物污染的重要原因[1-4].为有效控制露天堆场在自然风作用下的扬尘,需对堆场周围空气流动规律和料堆受力进行深入的研究.

风洞模拟实验是目前国内外学者研究开放性物料堆扬尘规律的主要研究手段.通过风洞模拟实验,测定颗粒物起动风速值,建立静态物料堆起尘量的实验关联式可以预测料堆的扬尘量[5],通过改变各影响因素测试扬尘量也已得到一些规律[6],但起动风速判定的主观性使得实验结果没有形成统一的结论.研究表明:物料堆场静态起尘量与风速、含水率和颗粒物直径有关[7-8],风速作为最重要的特征参数[9],直接体现了颗粒源释放有无和风蚀污染的可蚀程度,而在确定料堆周围风场分布方面,数值模拟方法较风洞模拟实验显示了公认的优势,随着计算机技术的高速发展,CFD(computational fluid dynamics)成为了解决各种流体流动强有力的工具[10],近年来国内外一些学者对开放性露天堆场和抑尘网的数值模拟为扬尘量的确定提供了一种思路[11-12],然而,我国在料堆周围速度场和表面受力的矢量性与扬尘关系上的研究较少.

本文应用FLUENT6.3软件对防风抑尘网后空气流动进行了数值模拟,获取了料堆表面受力的微观特性及分布规律,确定了防风抑尘网最佳孔隙率.

1 数值模拟

数值模拟分为3个步骤:预处理、求解和后处理.首先根据宏观量判定法确定计算区域,对计算域进行网格划分;第2步选取合适的紊流模型、算法及离散格式进行空气绕流的计算;最后调整防风抑尘网布置计算料堆表面的空气动力学参数.

1.1 控制方程及边界条件

对于开放性露天堆场周围空气绕流[13],认为空气是不可压缩,流动处于稳态、绝热和中性紊流大气层中,采用标准k-ε紊流模型[14],控制方程如下:

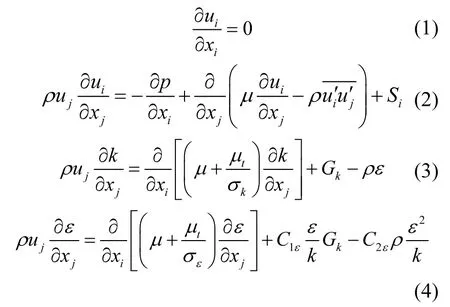
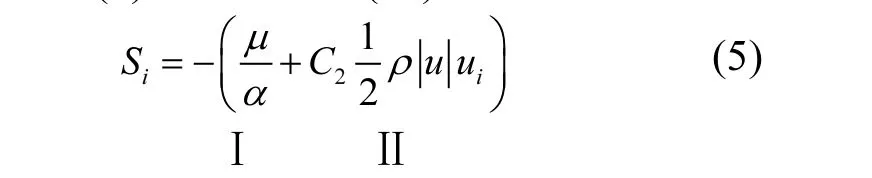
式中:α代表多孔介质的渗透性;C2是惯性阻力因子,多孔板上压强的损失因子:

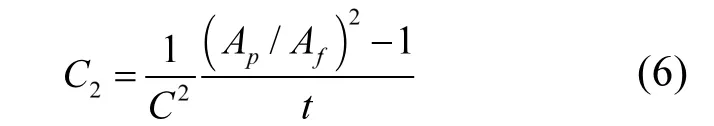
式中:Af为抑尘网孔的总面积;Ap为抑尘网的总面积(固体与孔的和);t为抑尘网厚度,取 1.5mm;C是随雷诺数(以孔径直径为特征长度,孔中流体的速度做特征速度确定)变化的系数,当Re>4000时,C近似等于0.98 ,本研究孔径雷诺数满足此条件,C取为0.98.其他参数选取见表1.

表1 数值计算参数Table 1 Input value for numerical simulation

传统意义上计算区域足够大的选取缺乏数据依据,虽然可以保证料堆周围空气流场不受计算区域影响,但会导致计算量庞大,本文采用料堆平顶面的剪切力这一宏观量作为判断标准,由小到大选取 7种计算区域工况,计算域和边界条件的设置如图 1所示,7种计算区域的参数见表 2.棱形料堆下表面长154m,宽51m,上表面长113m,宽10m,料堆高17m.

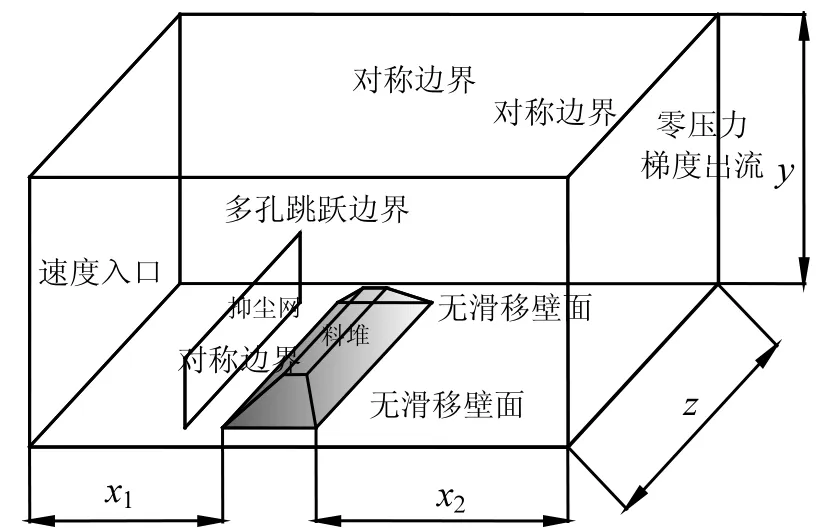
图1 计算区域和边界条件Fig.1 Computational domain and boundary conditions

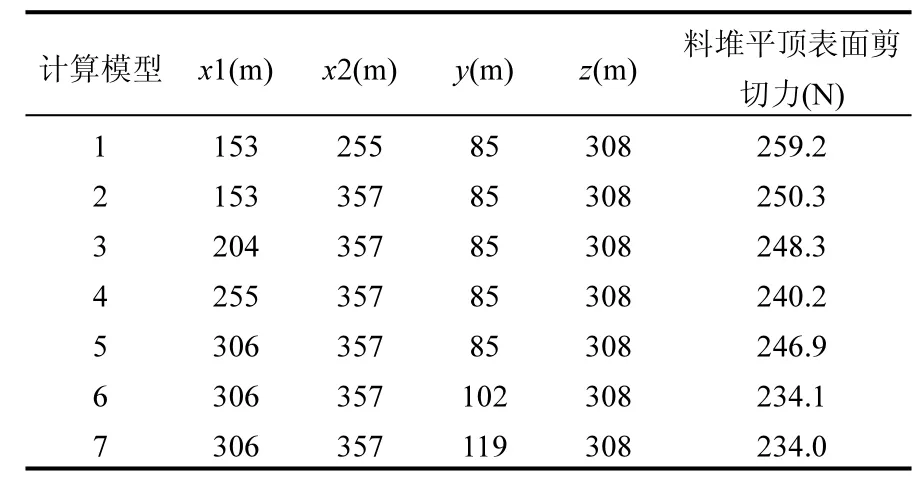
表2 计算域尺寸与料堆平顶面剪切力Table 2 Physical dimension of computational domain and the shear force on flat-top surface

从表2中7种工况可以看出:当计算区域长、宽、高分别为14倍堆宽(堆前6倍,堆后7倍)、2倍堆长、7倍堆高时,料堆平顶表面剪切力不再变化,故选择模型 7为计算区域,即 714m×119m× 154m.

1.2 紊流模型及网格划分

目前,国际上对绕流防风抑尘网周围流场的数值研究采用的模型主要分为2种:标准k-ε紊流模型和可实现 k-ε紊流模型.通过两种模型和实验数据对比的研究表明[11]:2种模型均可在整体上较好地反映流动特性,但在0.38倍抑尘网高度处标准k-ε紊流模型比可实现k-ε紊流模型更接近实验数据,在 1.88倍抑尘网高度处可实现k-ε紊流模型结果更好.鉴于本研究旨在探索料堆表面(0.77倍抑尘网高度处)剪切力及剪切层内空气的流动规律,故选择更为接近的0.38倍网高处结果更好的标准 k-ε紊流模型.对整个计算区域进行非结构化网格划分,当网格数为 1755883时计算结果与网格数不再有关,采用二阶迎风离散格式进行模拟,计算收敛误差为0.00001.

2 结果及讨论

2.1 露天堆场周围空气流场

应用以上模型对料堆周围空气流动进行数值模拟,计算结果如速度矢量图2所示.由图2可以看出,进口风速为 5m/s的空气流至料堆,在粘性力作用下沿迎风面贴附向上流动,随着流通断面积的减小,风速从坡面底部的 1.72m/s逐渐增大至顶部 8.32m/s,即迎风面向上扬尘,在冠顶达到最大;平顶表面上部空气与来流方向一致,平均风速为 6.3m/s;背风面上部在来流风作用下空气沿坡面(17m高)向下贴附流动至约11m高以下,后随着坡面向下空气动压降低,静压逐渐增大,在负压差作用下形成回流,在涡旋作用下空气沿坡面向上流动,这一特点在图3的表面剪切力上表现的更为显著.

由图3可以看出:迎风表面所受剪切力沿坡面平行向上,随高度逐渐增大,与前述流动速度变化相符,料堆颗粒在此剪切力作用下沿迎风表面上扬,且随高度增加扬尘加剧,至冠顶达到最大;平顶面剪切力变化较缓,沿来流方向最前部作用力最大,1/3至2/3长度区间稍有减小,2/3长度以后几乎不变,可见料堆颗粒在平顶面平行于来流方向扬尘;背风面剪切力明显小于迎风面和平顶面,从背风面顶部17m高度至11m高度,剪切力沿坡面向下(>0), 11m高度以下至底部,剪切力沿坡面向上(<0),即背风面上部在平顶面空气流动作用下,颗粒物继续沿坡面向下扬起,而在中下部区域在背风区涡旋回流作用下,料堆颗粒被风卷起向上扬起.

通过以上料堆周围空气流场和表面受力的空气动力学分析可见,迎风面和平顶面为主要扬尘表面,背风面扬尘量较少,因此对开放性料堆抑尘的重点在于减小迎风表面和平顶表面上空气流速和削弱表面剪切力作用,以下通过对防风抑尘网设置后空气流场结构的数值模拟来探究抑尘网对料堆微观受力分布的规律,从而为抑尘网优化提供科学依据.

2.2 抑尘网后空气流场的力学分布

将防风抑尘网置于料堆前削弱来流风动能,减小料堆表面空气作用力是目前公认的有效减低料堆扬尘的有效手段.在一定范围内防风抑尘网高度和离料堆距离对抑尘效率无影响[16],本研究选取推荐范围的网高 22m(料堆高度的1.3倍),抑尘网置于料堆前17m处(料堆高度的1倍),分别对孔隙率ε为0,0.2,0.4,0.6的抑尘网设置后空气流场进行了数值模拟,速度矢量场结果示于图4.

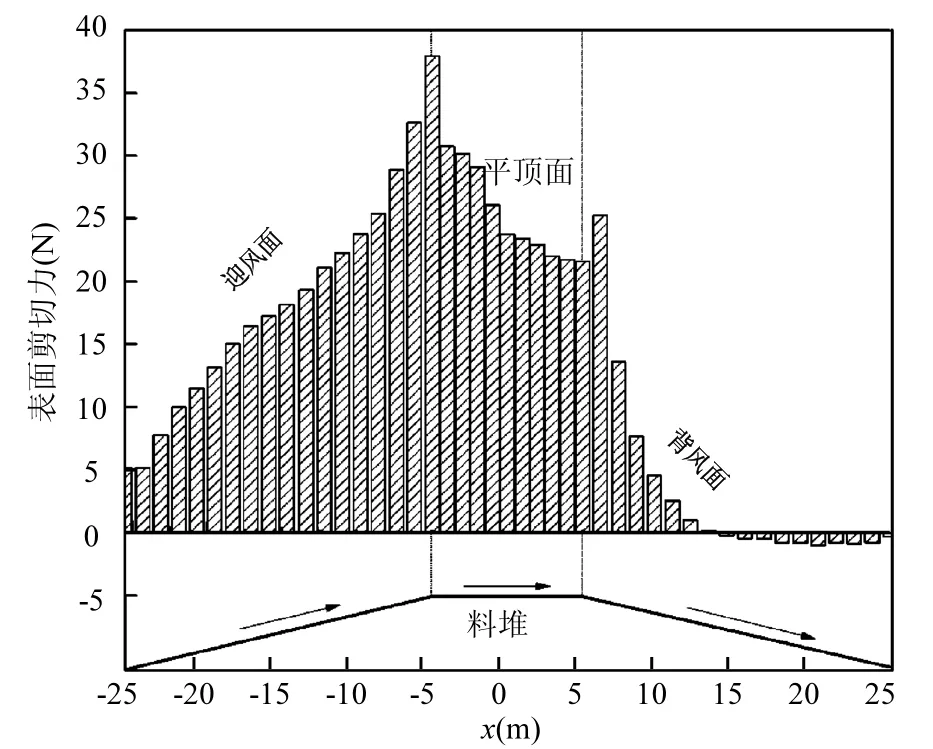
图3 料堆各表面剪切力分布Fig.3 Wall shear force on each surface of pile

图4 抑尘网后料堆周围空气速度矢量Fig.4 Velocity vector fields over the prismatic pile behind fence

由图4可看出:防风抑尘网孔隙率为0,即无孔挡风墙(或板)将来流风阻挡在料堆前,空气从挡风墙(或板)上部绕流,在越过挡风墙(或板)上部后流速达到最大值 6.61m/s,由于挡风墙(或板)与迎风面中间区域压力急剧降低,部分绕流空气在垂直压差作用下在这一区域形成涡旋,涡的中心高度较料堆顶部高,迎风表面风速沿坡面向下,料堆颗粒被吹向地面,沉积或被卷吸起.防风抑尘网孔隙率为 0.2时,最大风速位置与ε=0相同,最大风速值为 6.004m/s,抑尘网渗流空气量与绕流空气相比较小,防风抑尘网与迎风面之间区域仍形成涡旋,涡的中心位于料堆高度2/3处,涡旋强度和涡旋直径较之ε=0小,迎风表面风速同样沿坡面向下,料堆颗粒向下运动.随着孔隙率增大,抑尘网渗流空气比例增大,网后压力亦增大,当孔隙率为0.4时,网后最大风速减小至5.752m/s,与孔隙率为0与0.2不同的是,网后空气未形成回流,迎风表面空气沿坡面向上贴附流动,料堆颗粒被风扬起散至空气,抑尘原理也与前两者不同,未改变迎风表面的湍流结构和流速方向,但降低的风速使其扬尘量较无网小,还可起到抑尘作用.当孔隙率继续增大至 0.6时,网后流场结构几乎与无网工况无异,最大风速同样出现在迎风表面冠顶,且较孔隙率为0.4时大,抑尘作用几乎不明显.

通过以上分析可看出,当孔隙率ε >0.4时,抑尘网作用不明显,而ε <0.4时,出现了2种湍流结构,为了获得较优的孔隙率,下面定量分析不同孔隙率下的料堆表面受力,结果示于图5.

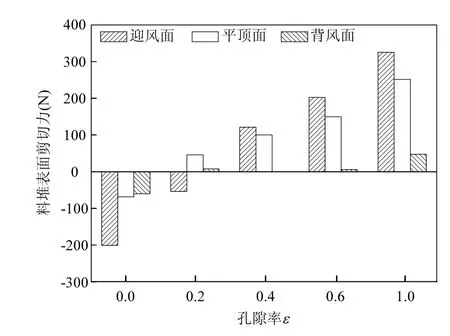
图5 不同孔隙率下料堆表面剪切力Fig.5 Shear force on the pile surfaces behind porous fence with deferent porosity

由图5可看出:3个表面中,迎风面和平顶面的表面剪切应力较背风表面大得多.迎风面在ε=0和0.2时剪切力为负值,即料堆颗粒在空气流动作用下向下滑至地面,且孔隙率为 0时的剪切力大于0.2,在ε=0.4和0.6时剪切力为正值,即料堆颗粒同未设网时(ε=1)相似,在网后空气贴附流动作用下向上扬至大气,且随孔隙率增大剪切力增大;对于平顶表面,当设置挡风墙(或板)时(ε=0),剪切力为负值,即在网后涡旋回流作用下平顶面逆向来流方向扬尘,且其绝对值大于孔隙率为0.2下的受力, ε=0.2、0.4和0.6时均为正值,即沿来流方向扬尘,并且随孔隙率增大而增大.综合以上计算结果可见:最佳孔隙率为0.2～0.4.

3 结论

3.1 料堆起尘与周围空气流速和料堆表面剪切力有关.在来流风作用下棱形料堆迎风表面和平顶面为主要扬尘面,背风表面被涡旋卷起扬尘量较前两者小得多.迎风表面沿坡面向上流速增加,在冠顶达到最大;平顶面剪切力沿流动方向几乎不变;背风面从顶部高度至2/3高度,料堆颗粒在剪切力作用下沿坡面向下扬起,2/3高度以下至底部在涡旋回流作用下,料堆颗粒被风卷起向上扬起.

3.2 防风抑尘网的设置改变了料堆周围空气的湍流结构,当孔隙率ε=0和 0.2时,在抑尘网和迎风表面中间区域出现涡旋回流,迎风表面空气沿坡面向下流动,颗粒在剪切力作用下向下滑至地面,且孔隙率为 0时的剪切力大于 0.2,对于平顶表面, ε=0时剪切力方向与来流方向相反,在网后涡旋回流作用下平顶面逆向来流方向扬尘,且其绝对值大于孔隙率为 0.2下的受力, ε=0.2、0.4和 0.6时扬尘与来流方向相同,并且随孔隙率增大而增大.综合流场结构和受力分布可得最佳孔隙率为0.2～0.4.

[1] 王帅杰,朱 坦.城市空气颗粒物开放源理论与治理技术研究进展 [J]. 城市环境与城市生态, 2003,16(6):193-194.

[2] 谢绍东,齐 丽.料堆风蚀扬尘排放量的一个估算方法 [J]. 中国环境科学, 2004,24(1):49-52.

[3] 林官明.近壁面猝发湍流对颗粒物起尘机理的探讨 [J]. 中国环境科学, 2008,28(7):599-602.

[4] Cao Junji, Shen Zhenxing, Chow Judith C., et al. Seasonalvariations and sources of mass and chemical composition for PM10aerosol in Hangzhou, China [J]. Particuology, 2009,7(3): 161-168.

[5] Gillette Dale. A wind tunnel simulation of the erosion of soil: effect of soil texture, sandlasting, wind speed, and soil consolidation on dust production [J]. Atmospheric Environment, 1978,12(8):1735-1743.

[6] Xuan Jie, Robins Alan. The effect of turbulence and complex terrain on dust emissions and depositions from coal stockpiles [J]. Atmospheric Environment, 1994,28(11):1951-1960.

[7] 丛晓春,陈志龙,詹水芬.露天煤场静态起尘量的实验研究 [J].中国矿业大学学报, 2010,39(6):849-853.

[8] 丛晓春,陈志龙,詹水芬.风蚀性粒子降尘浓度的动力学预报模式 [J]. 中国环境科学, 2012,32(7):1171-1176.

[9] Badr T, Harion J L. Numerical modeling of flow structures over various flat-topped stockpiles height: Implications on dust emissions [J]. Atmospheric Environment, 2009,43(35):5579-5587.

[10] Diego I, Pelegry A, Torno S, et al. Simultaneous CFD evaluation of wind flow and dust emission in open storage piles [J]. Applied Mathematical Modelling, 2009,33(7):3197-3207.

[11] Lee Sang-Joon, Lim Hee-Chang. A numerical study on flow around a triangular prism located behind a porous fence [J]. Fluid Dynamics Research, 2001,28(3):209-221.

[12] Lee Sang Joon, Kim Hyoung Bum. Laboratory measurements of velocity and turbulence field behind porous fences [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999,80(3):311-326.

[13] Jason A. Roney, Bruce R. White. Comparison of a twodimensional numerical dust transport model with experimental dust emissions from soil surfaces in a wind tunnel [J]. Atmospheric Environment, 2010,44(4):5579-5587.

[14] Chen Guanghui, Wang Weiwen, Sun Changfeng, et al. 3D numerical simulation of wind flow behind a new porous fence [J]. Powder Technology, 2012,230:118-126.

[15] Guo Li, Maghirang Ronaldo G.. Numerical Simulation of airflow and particle collection by vegetative barriers [J]. Engineering Application of Computation Fluid Mechanics, 2012,6(1):110-112.

[16] Bitog J P, Lee I B, Shin M H, et al. Numerical simulation of an array of fences in Saemangeum reclaimed land [J]. Atmospheric Environment, 2009,43(30):4612-4621.

Numerical simulation of turbulence structure and sheltering effect behind porous fences in open storage piles.

SONG

Chong-fang, PENG Lin*, BAI Hui-ling, MU Ling, LIU Xiao-feng (College of Environmental Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China). China Environmental Science, 2014,34(7)：1690～1695

This paper was conducted to predict the turbulence structure and sheltering effect behind porous fences in open storage piles. The numerical simulation of the three dimensional static flow field was performed applying the standard k-ε turbulence model; the airflow characteristics and the shear stress distribution on the windward side, flat top surface and leeward side of a typical prismatic material stack were analyzed; and the distribution of the aerodynamic structure of each surface of the storage pile was revealed based on the data of flow field for the porous fence with different porosity. Results indicated that the shear force on the flat top surface increased with increasing porosity, exhibited litter change with unfenced conditions. Regarding the windward side of the storage piles, a re-circulating flow in the region between the fence and the pile at low porosities and the shear force acted downward along the windward face, but rather, the shear force acted upward along the windward side at high porosities. Since the leeward side was always in the backflow region, the shear force on the prismatic leeside changed little with increasing porosity. The numerical predictions showed the porous fence with porosity between 0.2and 0.4was found to be the optimum. Through the aerodynamic simulation of each surface of the storage pile, the computation distortion caused by vector offset out of different directions of the shear force can be avoided.

open storage pile；numerical simulation；turbulence；porous fence

X513

A

1000-6923(2014)07-1690-06

宋翀芳(1974-),女,山西太原人,副教授,博士,主要从事大气颗粒物扩散及防治研究.发表论文10余篇.

《中国环境科学》获评“百种中国杰出学术期刊”

《中国环境科学》编辑部

2013-09-25

国家自然科学基金资助项目(51108295;41173002)

* 责任作者, 教授, plin123@eyou.com

《中国环境科学》2012年被中国科学技术信息研究所评为“2011年度百种中国杰出学术期刊”.“百种中国杰出学术期刊”是根据中国科技学术期刊综合评价指标体系进行评定的,包含总被引频次、影响因子、基金论文比、他引总引比等多个文献计量学指标.