谱修正技术在脉冲压缩信号检测中的应用

邹彬彬，陈晶晶，荆成财，王润田



谱修正技术在脉冲压缩信号检测中的应用

邹彬彬，陈晶晶，荆成财，王润田

(中国科学院声学研究所东海研究站，上海 200032)

脉冲压缩是信号检测的一个重要技术，在多目标水声环境下，为避免强目标脉冲压缩输出的旁瓣掩埋弱目标的主瓣，引入窗函数加权技术来抑制旁瓣，提高对目标的空间分辨率。同时考虑到实验中声呐系统的带宽和时宽受限制，对于小时宽带宽积的脉冲压缩信号，引入谱修正技术，进一步提高主旁瓣比。利用Matlab给出理论仿真结果，并通过实验验证该技术在噪声背景下对观测小目标的实用性。

脉冲压缩；抑制旁瓣；窗函数加权；谱修正技术；

0 引言

为了提高声呐系统的作用距离，在发射端平均功率允许的前提下，可增大脉冲宽度来提高信号的能量。但是在单频脉冲下，脉冲宽度直接决定了距离分辨率，这样就无法同时提高声呐的探测距离和距离分辨率。为两者兼顾，引入脉冲压缩技术[1]。线性调频信号(Linear Frequency Modulation, LFM)是研究最早、应用最广泛的脉冲压缩信号，具有对目标回波信号多普勒不敏感、技术较为成熟的优点。本文的仿真研究和实验验证中，均使用LFM信号作为脉压系统的发射信号。

1 数字脉冲压缩的理论和仿真

1.1 线性调频信号

LFM信号的表达式为：

瞬时频率()与时间成线性关系，对()做傅里叶变换可得LFM信号的频谱表达式为[2]

图1给出了时宽带宽积(TB值)分别为40和140的LFM信号的幅度谱仿真结果，其中信号频带分别为80~120 kHz和30~170 kHz，时宽均为1 ms。TB值越大，幅度谱越接近矩形。

由以上分析可知，作为发射信号，LFM信号在带宽内频率按线性规律变化，相位具有色散性。为了实现压缩，在接收端设置一个与发射信号相位共轭的压缩网络，其相位色散绝对值相等，符号相反，即线性调频信号的脉冲压缩是通过匹配滤波器来实现的[3]。根据匹配滤波理论，其传输函数为

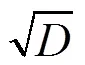
图2 脉冲压缩输出

1.2 窗函数加权技术

根据式()分析可得，输出的最大主旁瓣比是-13.49 dB，其它旁瓣按其离主瓣间隔按1/进行衰减，那么强目标信号的旁瓣可能会淹没弱目标信号的主瓣，造成目标丢失。为了提高声呐系统分辨多目标的能力，通常采用函数加权的方法来降低旁瓣，提高弱信号的检测能力[5]。工程中考虑旁瓣抑制，主瓣展宽，信噪比损失及实现难易程度，一般采取海明窗、汉宁窗、余弦平方等窗加权函数。本文采用海明窗进行频域加权，其表达式为

窗函数的加权可以通过修改匹配滤波器的传输函数来完成，加入海明窗后的传输函数为

图3是经过海明窗加权和未经过海明窗加权的脉冲压缩输出结果的仿真对比。

从图3可见，使用海明窗加权可以使主旁瓣比提升10 dB左右，并且主瓣展宽较小。

图3 经过海明窗加权的效果

1.3 谱修正技术

相对于雷达，声呐脉冲压缩系统一般都为小时宽带宽积的信号，小压缩比的LFM信号幅度谱不再具有近似的矩形特性，通带内的菲涅尔波纹较大，如图1所示，窗函数加权抑制旁瓣后仍然不能满足工作需求，因此对于较小的LFM信号，引入谱修正技术是十分有必要的。

谱修正就是将线性调频信号的频谱修正为矩形，使匹配滤波器的输出具有矩形，这样就有[6]

谱修正后的匹配滤波器传输函数为

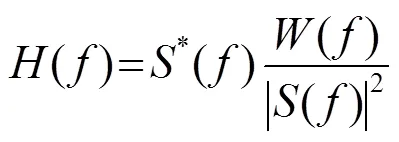
在频域上实现的脉冲压缩滤波器由四部分组成：带通滤波、匹配滤波、窗加权滤波和谱修正滤波。在频域进行数字脉冲压缩的流程如图4所示，其仿真结果如图5所示。

图4 频域脉冲压缩流程图

图5 经过谱修正的效果

由图5可知，引入谱修正技术后，主旁瓣比大幅提升，并且主瓣展宽和信噪比损失均较少。

2 实验结果及分析

脉冲压缩算法实现及水池实验使用的DSP芯片为ADI公司的定点DSP，它基于ADI和Intel联合开发的微信号架构，兼有DSP强大的信号处理能力和通用型微控制器的易用性，外设功能强大，极大地简化了系统的硬件和软件设计[7]。DSP处理流程图见图6。

图6 DSP处理流程图

2.1 小目标检测

实验室水池尺寸为4 m×2.1 m×2.8 m，池底目标繁杂，有钢管、塑胶管等杂物，收发合置换能器的位置在水下1 m处，回波信号的采集时间长度为2 ms，内核定时器的延时根据目标离换能器的位置进行调整，以确保目标在采集的时间窗内。所用换能器的中心频率为100 kHz，带宽为40 kHz，张角为20°。目标小球直径为12 cm，初始放置距离换能器的轴向为2m，并以此为参考点分别后移20 cm和55 cm。

使用ADSP的编译环境VDSP将采集的回波信号和脉冲压缩输出绘图如7所示。

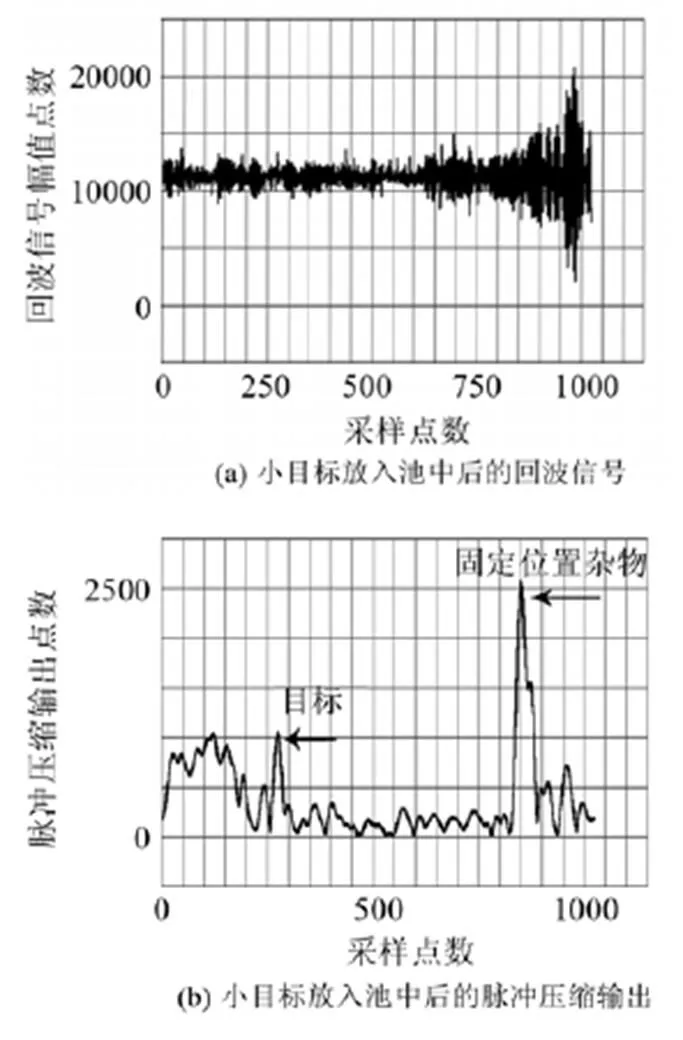
在图7的(b)、(d)和(f)中可以发现有个移动的小尖峰，便是目标小球。移动间距依照DSP输出计算为18 cm和51 cm。脉冲压缩技术可以将目标从杂乱无章的回波信号中识别出来，效果良好。误差主要来源于声速测定和目标摆放。

2.2 多目标识别

目标间距的测量实验，以检验脉冲压缩技术的距离分辨率。目标分别为池壁和一块40 cm×40 cm的方形铝板，两目标的测试间距分别为30、10和5 cm，回波信号和脉冲压缩输出结果如图8所示。

在图8的(a)、(c)和(e)中可以发现回波信号叠加现象严重，较难直观快速地对目标进行分辨和测间距，但经过脉冲压缩之后，由8(b)、8(d)和8(f)可见，两个目标尖峰清晰，计算间距分别为：29.5、11.5和4.1 cm，与目标实际间距吻合较好。误差主要来源于声速测定和目标摆放。在池壁峰值之后的尖峰为池中钢管。

3 结语

本文对基于线性调频信号的声呐脉冲压缩系统进行了较为全面的仿真，并且通过水池实验，对实际采集的脉冲压缩数据进行处理和分析，得到较好的效果，验证了窗加权谱修正脉冲压缩算法对于声呐系统的有效性。

[1] Mark A Richards. 雷达信号处理基础[M]. 北京: 电子工业出版社, 2007: 142.

Mark A Richards. Fundamentals of radar signal processing[M]. Beijing: Electronic Industry Press, 2007: 142.

[2] 张明友, 汪学刚. 雷达系统(第二版)[M]. 北京: 电子工业出版社, 2006: 254-255.

ZHANG Mingyou WANG Xuegang. Radar system[M]. Beijing: Electronic Industry Press, 2006: 254-255.

[3] Bassem R Mahafza, Atef Z Elsherbeni. 雷达系统设计MATLAB仿真[M]. 北京: 电子工业出版社, 2009: 169-170.

Bassem R Mahafza, Atef Z Elsherbeni. MATLAB Simulation for Radar Systems Design[M]. Beijing: Publishing House of Electronics Industry, 2009: 169-170.

[4] 郑力文, 孙晓乐. 线性调频信号数字脉冲压缩技术分析[J]. 现代电子技术, 2011, 34(1): 39-42.

ZHENG Liwen, SUN Xiaole. Digital pulse compression technology of linear frequency modulation signal[J]. Modern Electronics Technique, 2011, 34(1): 39-42.

[5] 徐玉芬. 现代雷达信号处理的数字脉冲压缩方法[J]. 现代雷达, 2007(07): 61-64.

XUE Yufen. Methods of Digital Pulse Compression in Modern Radar Signal Processing[J]. Modern Radar, 2007(07): 61-64.

[6] 张静. 脉冲压缩及其旁瓣抑制技术研究[D]. 西安: 西安电子科技大学, 2005: 22-23.

ZHANG Jing. Pulse compression and sidelobe supression technology[D]. Xi’an: A dissertation of the degree of master in Xidian University, 2005: 22-23.

[7] ADSP-BF50X Blackfin Processor Hardware Reference(Revision1.0). Analog Devices, Inc, 2010.

Application of pulse compression technique in underwater acoustic detection

ZOU Bin-bin, CHENG Jing-jing, JING Cheng-cai, WANG Run-tian

(Shanghai Acoustic Laboratory, Chinese Academy of Science, Shanghai 200032, China)

In order to solve the contradiction between operation distance and range resolution of the sonar, the principle of pulse compression is analyzed. The sidelobe suppression of linear frequency modulation signal (LFM) is introduced to avoid target omission. Considering the small product of timewidth and bandwidth of sonar system, the technique of modification to signal spectrum is adopted .The suggested algorithm is simulated by MATLAB and realized based on ADSP-BF506F in our experiment.

pulse compression; sidelobe suppression; signal spectrum modification

TB556

A

1000-3630(2014)-03-0275-05

10.3969/j.issn1000-3630.2014.03.018

2013-01-28;

2013-05-02

上海市科委“科技创新行动计划”资助项目(12231203800)。

邹彬彬(1989－), 男, 浙江舟山人, 硕士研究生, 研究方向为声学信号处理。

邹彬彬, E-mail: zoubinbin11@mails.ucas.ac.cn