中国人标准头模BHead210的头相关传递函数数值计算
唐玲,付中华
中国人标准头模BHead210的头相关传递函数数值计算
唐玲1,付中华2
(西北工业大学计算机学院,陕西西安 710129)
针对基于中国人平均头部尺寸的BHead210标准头模,通过结构光扫描获取三维数据并利用边界元方法计算其头相关传递函数。将刚球模型的计算结果与解析结果进行对比,验证了计算方法的正确性,并将BHead210的计算结果与测量结果对比以观察误差。给出了由边界元计算数据导出的BHead210双耳时间差、双耳声级差曲线与不同声源距离某方位的头相关传递函数幅度谱。最后对比和分析了BHead210头模数据与CIPIC公布的KEMAR头模数据的差异。
头相关传递函数;中国人标准头模BHead210;数值计算
0 引言
头相关传递函数(Head Related Transfer Function, HRTF)定义为自由声场下从声源到双耳的频域声学传输函数,它表达了生理结构对声波的综合滤波效果[1]。在虚拟声的研究领域中,尤其在双耳空间听觉研究方面,HRTF起着重要的作用。
获取HRTF的方法有实验测量和理论计算两种。实验测量可在消声室中进行,采用的是数字测量技术[2]。实验测量对实验环境和设备有很高的要求,需要大量的校准和均衡处理,是一项非常耗时的工作。理论计算则是通过求解头部、躯干、耳廓等组成的声学系统对声波的散射问题来获取HRTF[1]。近20多年来,许多研究工作者开展了理论计算HRTF的工作。1998年,Kahana等人采用边界元方法对KEMAR人工头HRTF的计算频率上限达到了6kHz,并且证明了与实验结果相符合[3]。2003年,TIAN Xiao等用时域有限差分法结合完全匹配层方法计算了球模型和KEMAR人工头的HRTF[4]。2004年,Fels等人为了研究HRTF随儿童生长的变化,通过数字照相获取儿童(4~6岁)头部三维信息并用边界元方法计算了儿童的HRTF[5]。2007年,Wolfgang等人应用由传统边界元发展而来的多级边界元方法计算HRTF,大大提高了理论计算的速度[6]。
目前,国外已经公开部分的人工头及真人的HRTF数据库,如MIT的Gardner等于1994年对KEMAR人工头进行测量获得的HRTF数据库[7],加州大学Davis分校CIPIC实验室的Algazi 和Duda等于2000年通过测量获得的真人与KEMAR人工头的HRTF数据库[8]。国内华南理工大学谢菠荪教授等于2005年底也通过对52名受试者的测量获得了相应的中国人头的HRTF数据库[1]。
HRTF是具有个性化特性的物理量,它与人体头部、耳廓、躯干等生理结构有着密切的联系,国外的数据库是基于西方人的生理特征而建立的,然而中国人在生理外形和尺寸上与西方人有一定差别,所以国外数据库不一定完全适用于中国人[1]。中国传媒大学依据中国成年人头面部尺寸的国家标准设计与制作了仿真头模BHead210[9],获取BHead210的HRTF工作也刚刚展开。本文基于边界元法,通过对BHead210扫描获取三维信息计算其HRTF。
1 边界元法计算HRTF
1.1 原理简介
边界元法(Boundary Element Method, BEM)是以边界积分方程为控制方程,对边界进行分单元离散,再将所有单元上的控制积分方程整合为代数积分方程组进行求解。




边界元分为直接边界元与间接边界元,直接边界元的计算区域只能在边界腔体的内部或外部,而间接边界元的计算区域则是整个空间[10]。边界元方法的一个关键问题是,对于某些频率会产生奇异值,这是因为线性方程组的求解矩阵不满足非奇异条件使得在该频率不存在唯一的解。直接边界元方法可以应用亥姆霍兹积分公式方程组(Combined Helmholtz Integral Equation Formulation, CHIEF)[11]方法解决解的非唯一性问题,尽管如此,间接边界元方法比结合了CHIEF的直接边界元法能更好地处理奇异问题[12]。
若分别计算不同距离、不同方位声源的HRTF将耗费许多时间,使用声学互易原理可以大大减少计算量。声学互易原理指在线性声学范围内,从发射点到接收点之间的声学系统是一个互易系统[13]。
本文采用LMS公司的Virtual.Lab Acoustic软件(简称VL)[14]中的边界元模块中的间接边界元方法来计算HRTF数据。
1.2 中国人工头模型及扫描
中国人标准头模BHead210是按照中国成年人头面部尺寸国家标准GB/T 2428—1998设计与制作的仿真头模(如图1所示),其头形参数、结构均比较符合中国人的特点[9]。在该头模上安装的耳廓模型,是在对中国成年男女耳廓形态进行了群体研究的基础上,选取最具有代表性的耳廓外形结构作为参考而设计制作的“平均耳”模型(或标准耳廓)[9]。该头模在耳道入口处放置了两个微型麦克风,因此可以通过实验测量获取HRTF数据并与数值计算结果进行比较分析。

图1 BHead210标准人工头模
在计算HRTF之前,首先要获取人工头模的三维扫描结果,并合理划分表面网格。下面介绍建立头模网格模型的方法,主要分为三维扫描与网格处理两步。
首先用扫描方法获取头模的三维结构信息。通常可以采用激光三维扫描仪或结构光三维扫描仪进行扫描。本文使用DAVID结构光三维扫描仪[15]来获取头模信息。结构光三维扫描仪相对于激光三维扫描仪有设备便携、成本低等优点[15]。结构光三维扫描仪一次只能扫描到光直射的范围,因而需要对头模的各个面分开进行扫描。扫描完成后,将所有面融合成一个完整的人工头模型。融合的结果可能会在交接处不光滑,可以利用三维软件将之平滑。扫描得到的结果是以obj文件格式保存的,在该文件里包含了组成头模的三角形面网格信息,约有63万个三角形网格,平均边长为0.8 mm。
在边界元计算中,分析频率上限的条件是:模型最大的网格边长应在所要计算的最短波长的1/4~1/6之间[16]。若计算的上限频率为10 kHz,则网格的最大边长约为6.7 mm。通过扫描得到的网格模型并不理想,不仅网格数量过多增大了计算量,而且由于融合过程中分辨率的不同导致网格大小可能不均匀,在光滑的部分网格边长过大,在精细部分边长又过小,如头顶的网格边长相对于耳朵要大得多,因此需要对网格模型进行处理。首先将扫描得到的网格模型进行从小到大的合并,减少网格数量。本文采用了rapidform软件[17]的decimate功能对扫描结果进行网格合并。网格合并得到的新网格模型保留了原网格模型的特点:平滑处的网格边长较大,非平滑处的网格边长很小,其中耳朵处的结构最为复杂,所以该处的网格最小(如图2所示)。网格合并时保证耳朵处网格边长为4 mm,其他部位的网格均大于4 mm。接着需要对平滑处过大的网格再细分,使其满足计算条件。细分方法是,将边长大于6.5 mm的三角形网格沿该边长对半分成两个三角形,直到所有边长均小于6.5 mm为止(结果如图3所示)。最后,将新的网格模型在rapidform中再进行网格的重新划分,本文利用了rapidform中的remesh功能[17]。经过上面的重新整理,新的网格模型边长都在4~6.5 mm之间,满足HRTF的计算要求,总单元格数为2.5万(如图4所示)。网格的处理过程中,软件并未改变头模形状,所以处理后的结果将不影响计算结果。

图2 处理前耳朵处网格与头顶处网格对比
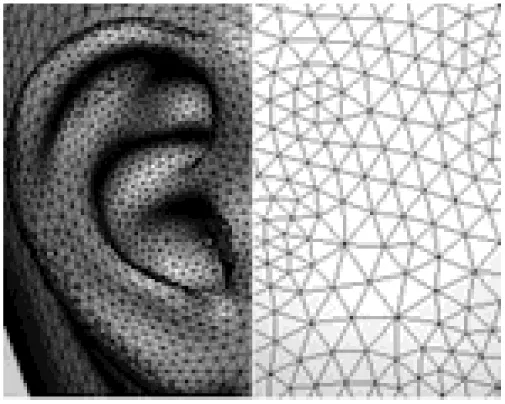
图3 处理后耳朵处网格与头顶处网格对比

图4 人工头网格模型
2 计算结果与分析
刚球模型是分析HRTF数据的最简单模型,为了验证边界元计算方法的正确性,将刚球模型的边界元法计算结果与解析结果进行了对比并分析误差。随后给出了中国人标准头模BHead210的HRTF相关数据,包括边界元法计算结果与实际测量结果的部分方位对比图、由计算得到的HRTF数据导出的双耳时间差与双耳声级差曲线、某方位不同声源距离的HRTF幅度谱等。实验测量目前仍然是获取HRTF数据最为准确的方法,因而有必要将计算与测量结果进行对比。双耳时间差()、双耳声级差()是声源的定位重要因素,可通过HRTF数据计算得到。此外,理论计算相对于实验测量,还有容易获取近场HRTF的特点,可方便地计算不同声源距离的HRTF以分析HRTF与声源距离的关系。最后将BHead210头模的计算结果与CIPIC公布的KEMAR头模数据进行了对比,观察BHead210数据与KEMAR数据的差异。
2.1 刚球模型HRTF
刚球模型是略去了耳廓、躯干等作用,把人头简化为半径的刚性球体,瑞利是最早采用刚球模型分析双耳声压的。Duda等利用球体对点声源产生的球面波的散射公式,得到了球体模型的HRTF解析公式[18]:
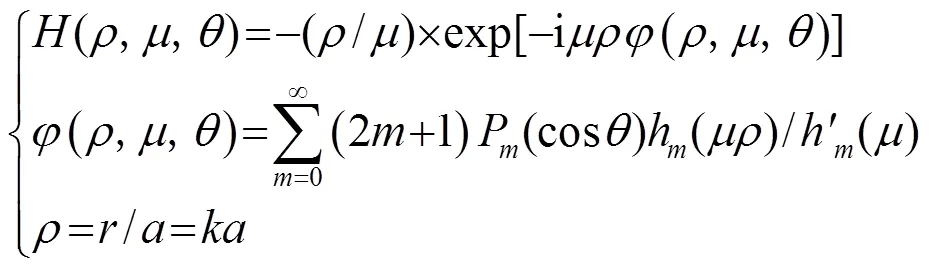
取刚球体半径为87.5 mm,声源位置离球中心为1.5 m,分别用边界元方法与式(3)计算HRTF,计算频率范围为100~10000 Hz,步长为70 Hz,将得到的结果进行对比(如图5所示)。图5中角度为球中心到球面观测点(耳朵位置)的直线与声波入射方向之间的夹角,如0°表示声源与观测耳同侧,90°表示正前方,180°表示声源与观测耳异侧。
在低频处,边界元计算结果与理论结果相差甚小,随着频率增高,误差会相对大一些。此外,声源与耳朵同侧时(如0°曲线),边界元计算结果误差比较小,而当声源与耳朵异侧时(如150°、180°曲线),计算误差会相对增大。得到的实验数据中,最大绝对误差不超过1.2 dB,所以我们采用的边界元法计算刚球模型HRTF误差是可以接受的。

图5 球体HRTF
2.2 中国人工头HRTF
本节给出了HRTF计算结果与测量结果的对比图(见图6),同时为了观察HRTF数据的基本特性,通过边界元计算得到的HRTF数据导出了双耳时间差()、双耳声级差()曲线(如图7、8所示),并计算了不同声源距离下某方位的HRTF幅度谱(图9、10)。
图6是水平面个别方位上BHead210的HRTF数据边界元计算与实验测量结果对比图,其中实验测量结果来自中国传媒大学的传播声学研究所[9]。将头模中心设置在连接两耳线段的中心点,点声源放置于离头模中心距离1 m处,观察点为耳道入口处。在边界元法计算中,假设头模为理想的刚体模型,计算频率范围为0~12 kHz,步长为70 Hz。图中分别给出了仰角0°(即水平面),方位角0°(正前方)、90°(正右方)、180°(正后方)、270°(正左方)的左耳HRTF幅度谱。
从图6可以看出数值计算方法和实验测量结果比较接近,曲线走势基本一致。进一步观察数据结果时发现,在高频部分,绝对误差会有所增大,而且部分方位的计算与实验测量结果还存在较大的偏差(如观测耳的异侧方向)。耳廓谷的位置和幅度值在某些方位有明显差异,正前方差异较大,正后方与观测耳的同侧方向的差异在1 kHz以内。数据上造成的不一致性可能来自于头模的刚性假设与扫描误差,在主观听觉上也需要进一步地探讨。
为了进一步验证计算结果,我们将计算得到的HRTF数据导出了、曲线。是声源方向定位的一个主要因素,在频率小于约1.5 kHz的低频段,它对方向定位起着重要的作用。在频率约为1.5~4 kHz的情况下,、对方向定位共同起作用。在频率大于4~5 kHz的高频段,是方向定位的主要因素。
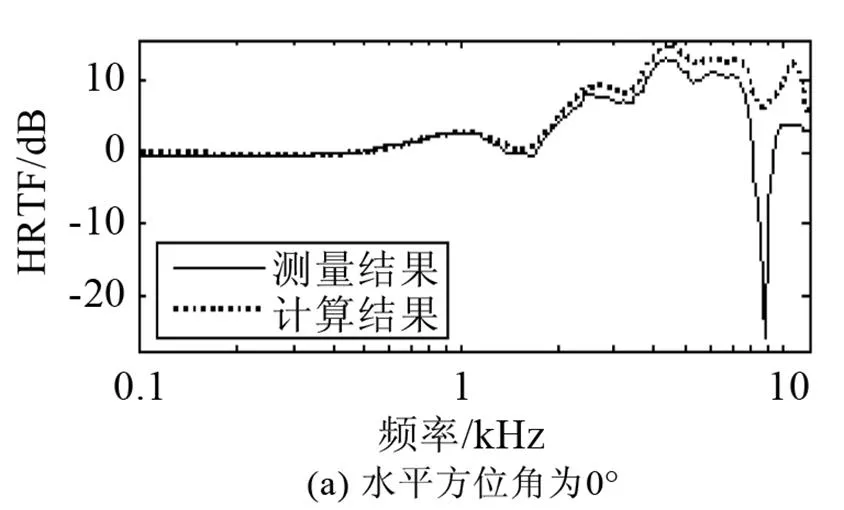
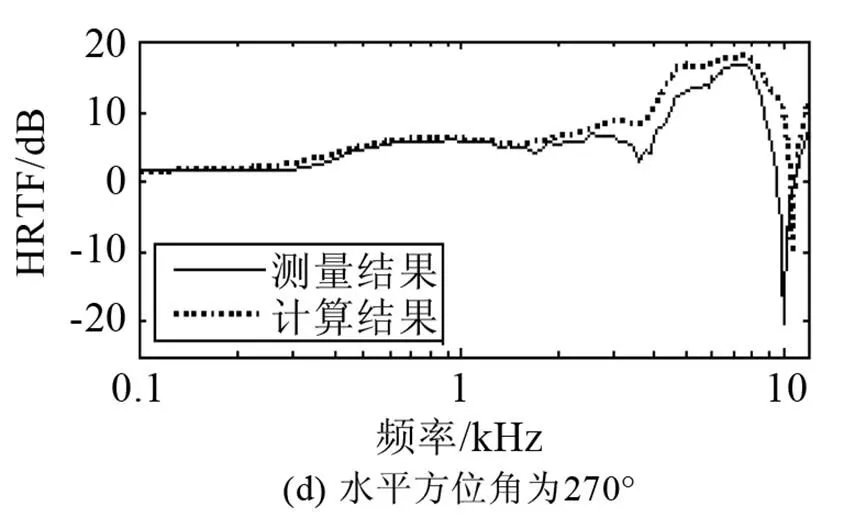
图6 BHead210计算及测量结果对比图
图7为由计算得到的HRTF导出的曲线,本文采用的是频域的相关法计算,得到的结果是全频带范围的“平均”。如图7所示,在方位角0°与180°处为0,随着声源接近侧向,增加,在侧向附近达到最大。
图8为不同频率下的曲线,在低频处很小,且随方位角的变化也很小。随着频率增大,曲线也变得复杂,如1.4 kHz、2.8 kHz的曲线最大值并不在90°方向,这是由于声波通过头的前、后、上方绕射并相干叠加到达异侧耳而形成的声压亮点。
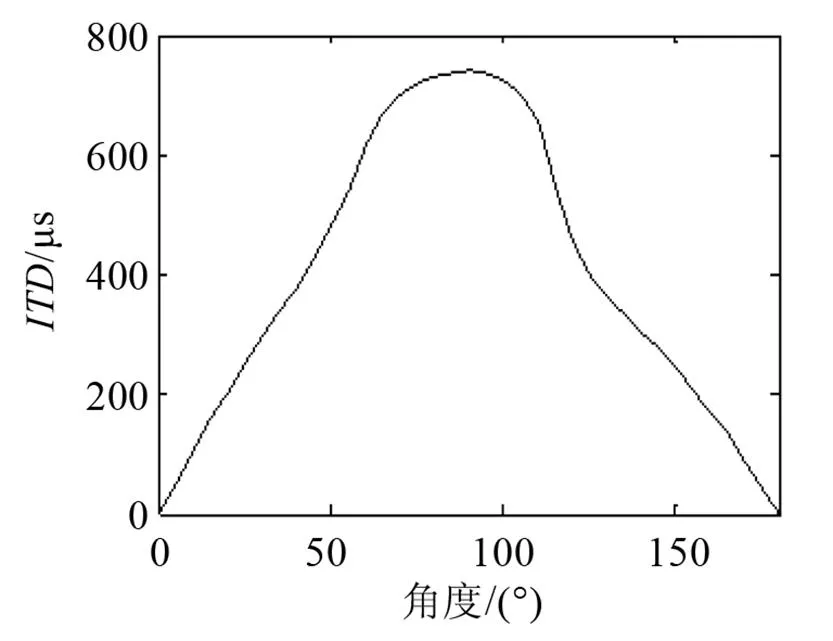
图7 ITD曲线
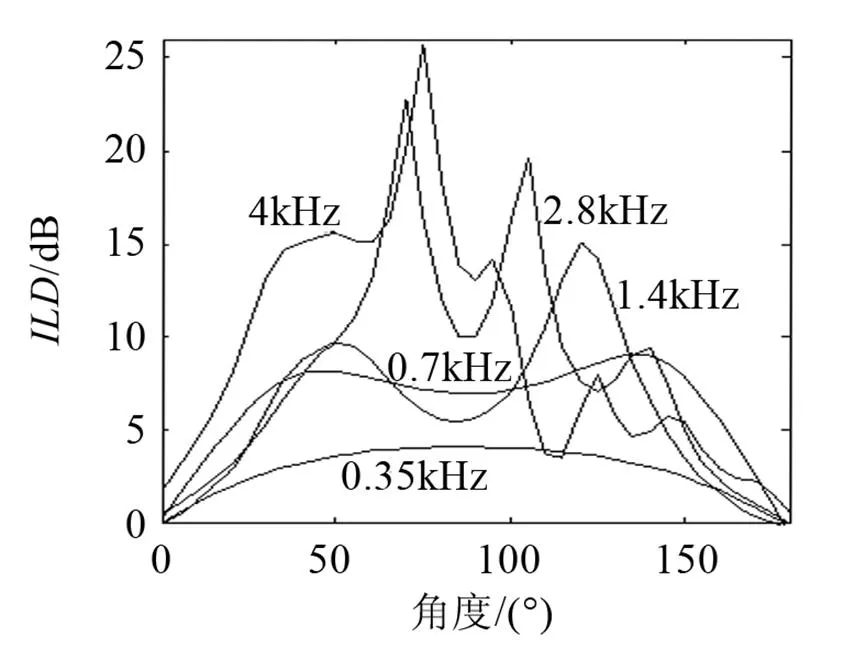
图8 ILD曲线
为了观察声源距离与HRTF数据的关系,图9、10给出了声源处于不同距离下,水平面方位角分别为90°、270°的左耳HRTF幅度谱,计算条件与前面所提的一样。实验测量获取近场HRTF数据是有一定困难的,理论计算则可以容易地获取不同声源距离的HRTF数据。从图中可看出,当声源距离小于0.5 m时,幅度谱的变化随距离的变化比较大。随着声源距离的增加,幅度谱的变化也逐渐变小。因而,在声源距离大于1~1.2 m时,HRTF的测量与分析可作为远场处理,近似于距离无关。
2.3 中国人工头与KEMAR人工头对比
HRTF数据是与人体头部、躯干、耳廓等外形尺寸和结构有关的具有个性化特征的物理量。国外公开的HRTF数据是以外国人特征为基础获得的。BHead210头模是依据中国人的平均标准特征而设计,我们将计算得到的BHead210的HRTF数据与CIPIC公布的KEMAR人工头模HRTF数据进行对比,以观察两者的差异。
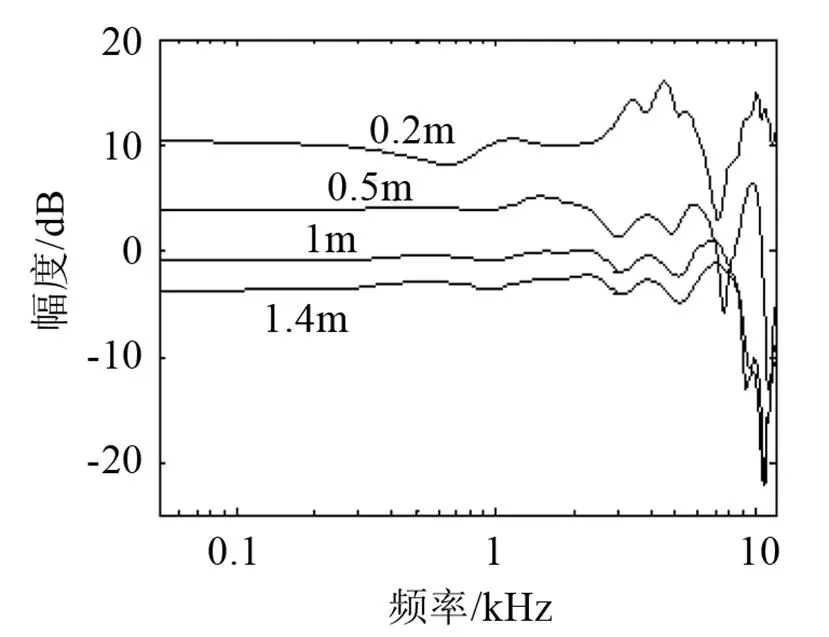
图9 90°左耳不同距离HRTF幅度谱

图10 270°左耳不同距离HRTF幅度谱
图11为声源距离在1m处产生的水平面0°(正前方)、90°(正右方)、180°、270°的中国人工头BHead210与KEMAR人工头的右耳HRTF数据结果图。BHead210的数据为边界元计算数据,计算条件与前面所提一样。KEMAR人工头配有大小号耳廓,数据为测量数据,观测点在耳道入口处[8]。KEMAR人工头的说明书建议小号耳廓适用于欧美女性和日本人,而大号耳廓适用于欧美的男性。
观察对比图,KEMAR的大小耳廓的HRTF值在低频段是相近的,只有在高频处才出现明显差异,耳廓谷的方位和大小也有所差异。相比之下,KEMAR与BHead210的结果在整个频段都有一定差异。在低频段,KEMARA与BHead210在正前方0°位置差异较大。在高频段,BHead210与KEMAR差异也比较明显,尤其是异侧耳处的耳廓谷方向。这些差异在主观听觉上的影响还有待进一步研究。

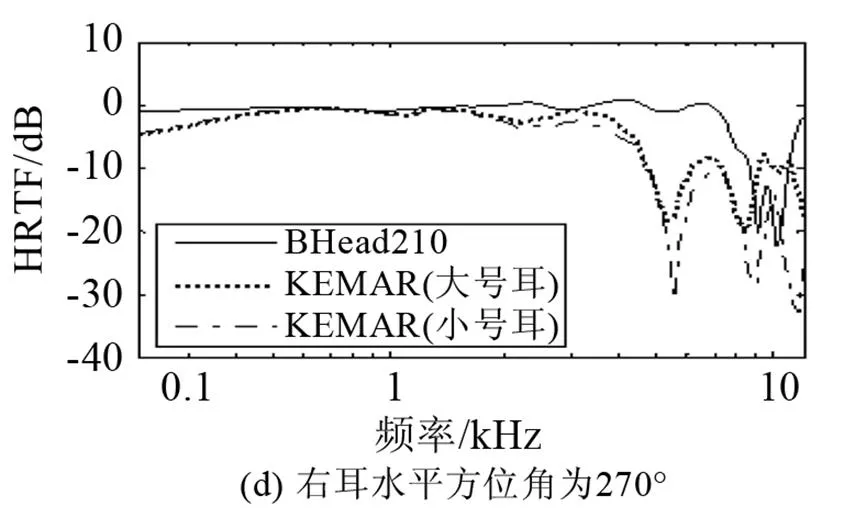
图11 中国人工头与KEMAR的HRTF对比图
3 结 论
HRTF包含了声源的空间定位信息,它是一个具有个性化特性的物理量,通过实验获取HRTF是一项复杂的工作,理论计算可使工作得到简化。获取中国人标准头模BHead210的HRTF数据,可为分析中国人虚拟听觉特性提供一些数据基础。本文介绍了获取中国人标准头模BHead210的HRTF数据的理论计算方法,首先通过结构光扫描和网格整理获得了BHead210的三维网格结构模型,然后采用边界元方法结合互易原理计算出不同方位的HRTF数据。对比了刚球的解析结果和边界元计算结果,验证了边界元方法的正确性,然后将中国人标准头模BHead210的计算结果与实际测量结果进行误差分析,并给出了由计算的HRTF数据导出的、曲线以及不同声源距离的HRTF幅度谱以分析HRTF特性,最后还将计算得到的BHead210人工头的HRTF与CIPIC公布的KEMAR人工头的HRTF数据进行对比。
致谢:作者在此衷心地感谢来自中国传媒大学的传播声学研究所的齐娜老师,她为本文提供了中国标准头模BHead210的实验测量数据。
[1] 谢菠荪. 头相关函数与虚拟听觉[M]. 北京: 国防工业出版社, 2007.
XIE Bosun. Head related transfer function and virtual auditory [M]. Beijing: National Defence Industry Press, 2007.
[2] Fukudome K, Suetsugu T, Ueshin T. The fast measurement of head related impulse responses for all azimuthal directions using the continuous measurement method with a servo-swiveled chair[J]. Applied Acoustics, 2007, 68(8): 864-884.
[3] Kahana Y, Nelson P A, Petyt M. Boundary element simulation of HRTFs and sound fields produced by virtual sound imaging system[C]// AES 105 Convention, San Francisco, CA, USA, 1998.
[4] LIU Tiao, XIAO Qinghuo. Finite difference computation of head-related transfer function for human hearing[J]. J. Acoust. Soc. Am, 2003, 113(5): 2434-2441.
[5] Fels J, Buthmann P, Vorlander M. Head-related transfer functions of children[J]. Acta Acoustia United with Acustica, 2004, 90(5): 918-927.
[6] Wolfgang Kreuzer, Zhensheng Chen. A fast multipole boundary element method for calculating HRTFs[C]// AES 122ndConvention, 2007, May5-8.
[7] Lkulish Antani, Nico Galoppo, Adam Lake, et al. MIT database, The university of North Carolina at Chapel HILL, http://sound.media.mit.edu/resources/ KEMAR.html.
[8] “CIPIC database,” http://interface.cipic.ucdavis.edu.
[9] 仝欣, 齐娜. 椭球头模与仿真头模的指向性比较[J]. 电声技术, 2012, 36(6): 43-46.
TONG Xin, QI Na. Comparison of the directivity between the ellipsoid head and the dummy head[J]. Audio Engineering, 2012, 36(1): 43-46.
[10] 祝家麟, 袁政强. 边界元分析[M]. 北京: 科学出版社, 2009.
ZHU Jialin, YUAN Zhengqiang. Boundary element analysis[M]. Beijing: Science Press, 2009.
[11] Schenck H A. Improved integral formulation for acoustic radiation problems[J]. J. Acoust. Soc. Am, 1968, 44: 41-58.
[12] Przemyslaw Plaskota, Andrzej B. Dobrucki. Head-Related Transfer Function calculation using Boundary Element Method[C]// Audio Engineering Society, 2007, May 5-8.
[13] 杜功焕, 朱哲民, 龚秀芬, 等. 声学基础[M]. 南京: 南京大学出版社, 2001, 3.
DU Gonghuan, ZHU Zhemin, GONG Xiufen, et al. Acoustic foundation[M]. Nanjing: Nanjing University press, 2001, 3.
[14] 李增刚, 詹福良. Virtual.Lab Acoustics 声学仿真计算高级应用实例[M]. 北京: 国防工 业出版社, 2010.
LI Zenggang, ZHAN Fuliang Virtual.Lab Acoustics acoustic simulation advanced application examples[M]. Beijing: National Defence Industry Press, 2010.
[15] “Structured Light Scanner”, http://www.david-laserscanner.com
[16] WU T W. Bonduary Elements in Acoustics[M]. WIT Press, Southampton, 2000.
[17] 333 Three D Systems Circle Rock Hill, SC 29730, USA, http://www.rapidform.com/
[18] Duda R O, Martens W L. Range dependence of the response of a spherical head model [J]. J. Acoust. Soc. Am., 1998, 104(5): 3048-3058.
Numerical method for calculating head-related transfer function of the Chinese dummy head BHead210
TANG Ling1, FU Zhong-hua2
(School of Computer Science, Northwestern Polytechnical University of China, Xi’an 710129,Shaanxi, China)
A numerical method for calculating the head-related transfer function (HRTF) of the Chinese dummy head BHead210is studied. With the Chinese dummy head BHead210, a structured light scanner is used to obtain its three dimensional data and then the boundary element method is used to calculate its HRTF. The calculation results with a rigid simple sphere model verify its correctness. The comparison results of the numerical calculation and those obtained by acoustic measurement are given. The Interaural Time Difference and Interaural Level Difference curves, different source-distance of HRTF amplitude spectrum are given too. The HRTF of the BHead21 is also compared to those of KEMAR reported by CIPIC.
head-related transfer function; Chinese dummy head BHead210; boundary element method
TN912
A
1000-3630(2014)-03-0237-06
10.3969/j.issn1000-3630.2014.03.011
2013-06-30;
2013-10-12
唐玲(1987-), 女, 海南儋州人, 黎族, 硕士研究生, 研究方向为 虚拟听觉。
唐玲, E-mail: tangling923@mail.nwpu.edu.cn
——护肾

