自适应神经网络模糊小波语音消噪算法
孙燕
自适应神经网络模糊小波语音消噪算法
孙燕
(青海民族大学计算机学院,青海西宁 810007)
针对有色噪声,采用自适应神经网络模糊系统模糊(Auto Neural Fuzzy Inference System, ANFIS)逼近有色噪声,利用自适应神经模糊推理系统ANFIS对噪声的非线性动态特性进行建模,提出了语音自适应神经网络模糊小波消噪算法,建立并训练了消噪系统。对被有色噪声污染的测量信号经模糊消噪后,根据信号和噪声的小波系数在不同分解尺度上的传递性,进行中值滤波和小波重构,得到了干净的语音。对算法进行了仿真实验,结果表明,消噪效果明显。
自适应神经网络模糊系统;小波;有色噪声;消噪;
0 引言
信号淹没在噪声中,是在实际环境中经常遇到的情况,当这种噪声为加性高斯白噪声时,可以采用线性滤波的方法,它是最基本的减谱算法[1],适用于对加性噪声的消除。目前消除非加性噪声的方法有自适应滤波如卡尔曼滤波[2]、维纳滤波[3]、谱减法及其改进等,卡尔曼滤波可以在一定程度上对有色噪声消除有效。维纳滤波法对背景噪声白化效果比较好。但对于噪声具有非线性传播性质时,使用线性滤波效果很差。有色噪声可看作是白噪声经过非线性动态处理后产生的,使用经典线性滤波的方法起不到抑制噪声的作用。
目前语音增强的方法很多:如谱减法及改进,它是应用最早最广泛的一种方法。它是从带噪语音频谱中减去噪声频谱分量,剩余的就是干净语音的频谱。其缺点是存在音乐噪声。信号子空间法[4]是把带噪语音分解成信号子空间和噪声子空间上的投影,在残余噪声频谱小于规定门限的情况下,使语音信号失真最小。缺点是主要针对加性宽带高斯白噪声。
本文利用自适应神经模糊推理系统ANFIS[5]对非线性动态特性进行建模逼近有色噪声[6],再利用小波变换[7]把含噪信号分解到多尺度中,然后在每一尺度下把属于噪声的小波系数去除,保留并增强属于信号的小波系数,最后重构出小波消噪后的信号得到有用信号。
针对实际环境的非线性有色噪声,本文结合经典谱减法的优点及利用自适应ANFIS对高斯白噪声非线性动态建模逼近有色噪声和小波阈值分解的优点,有效消除了有色噪声,解决了经典算法对有色噪声无效的问题。
1 ANFIS结构
1985年Takagi和Sugeno提出了一种非线性T-S模糊模型,即后来的Sugeno模糊模型[8],是一种对有精确输入、输出数据集产生模糊规则推理的系统化方法。它结合模糊逻辑与神经网络两者之优势,改善了传统模糊控制设计中必须人为调整隶属度函数以减小误差的不足,采用混合学习算法调整前提参数和结论参数,自动产生模糊规则。后来,Tang Roger提出与一阶Sugeno模糊模型功能等同的基于自适应神经网络的模糊推理系统(ANFIS)[8,9]用来实现Sugeno模糊模型的学习过程。该网络是一个多层前馈网络[10,11],结构如图1所示。
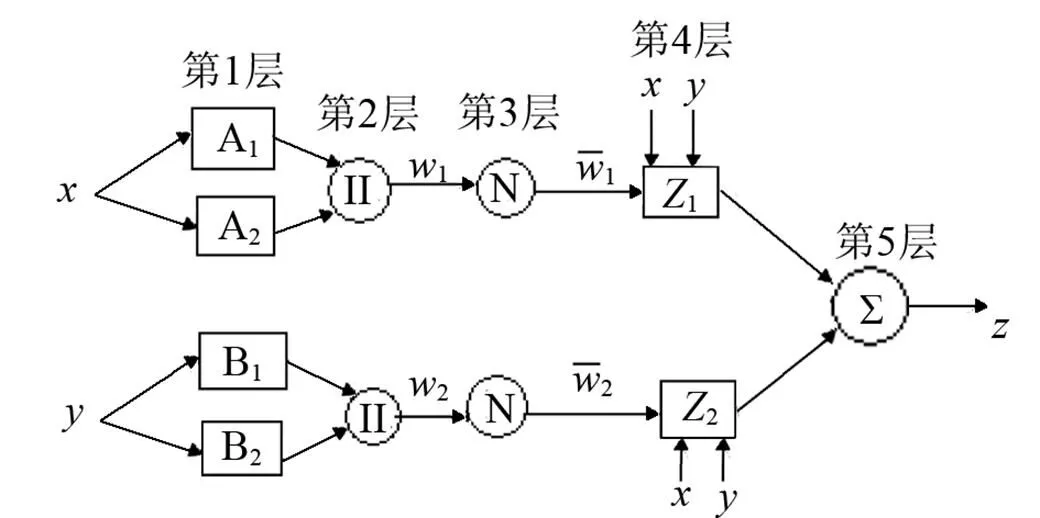
图1 Sugeno模糊系统等效的ANFIS网络
由图1可见,网络共有5层,各层功能如下:
第1层:A和B为输入变量的模糊子集,该层节点的激活函数代表模糊变量的隶属函数,该层的输出代表模糊化结果,即隶属度,其中一个节点的传递函数可以表示为:
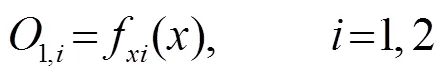
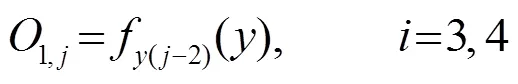
第2层:将模糊化得到的隶属度两两相乘,该层的输出代表着模糊规则的强度或适用度。
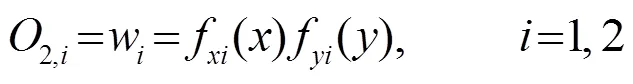
其中用表示上一层的隶属度。
第3层:将各条规则的适用度归一化:

第4层:计算每条规则的结论:

第5层:计算所有规则的输出之和,即系统输出:

2 自适应神经网络模糊小波消噪原理
自适应神经网络[12]模糊小波消噪原理见图2。
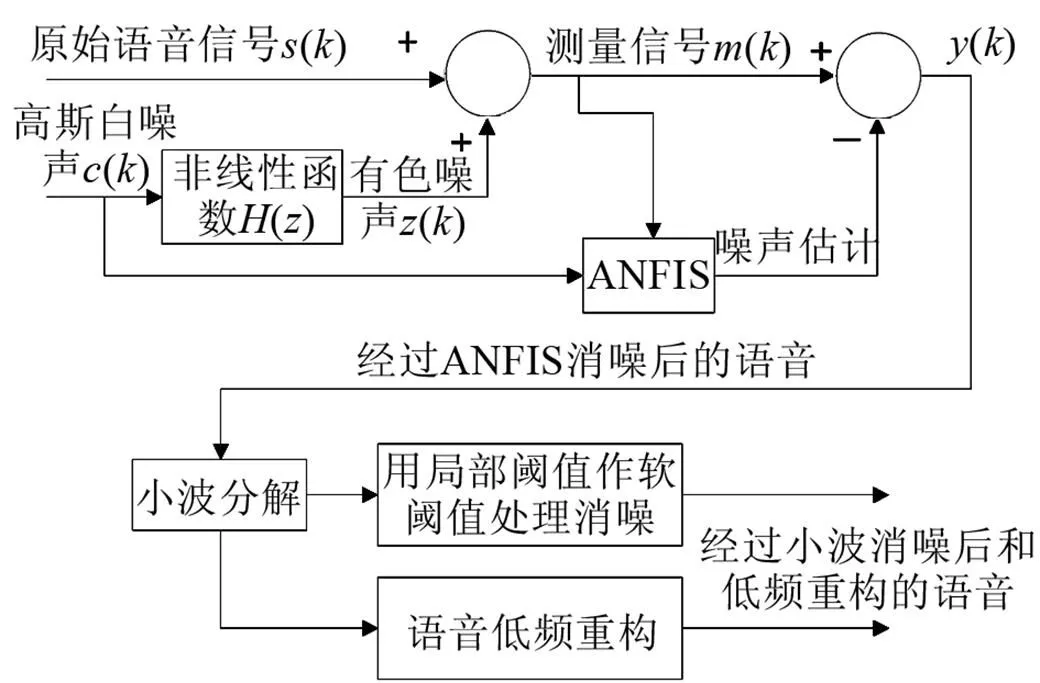
图2 语音自适应神经网络模糊小波消噪原理
自适应神经网络模糊小波消噪是将高斯白噪声与其延迟和测量信号作为系统训练集,通过ANFIS系统模糊逼近测量信号中的有色噪声,从被有色噪声污染的测量信号中减去逼近的噪声,再经过小波的低通滤波将高频噪声滤除得到干净的语音信号。
2.1 ANFIS噪声估计
有色噪声为白噪声通过下列非线性函数后产生:
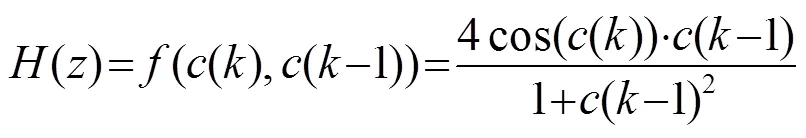
仿真实验非线性函数特性曲线就是由这个函数构造得出的,如图4所示。
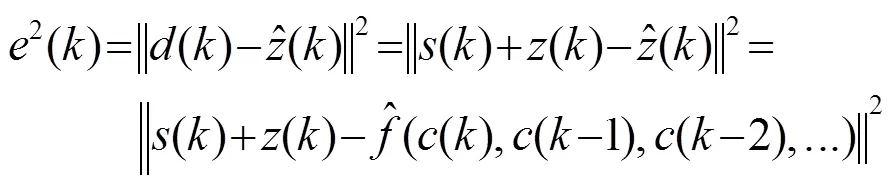
将式(7)展开,得到
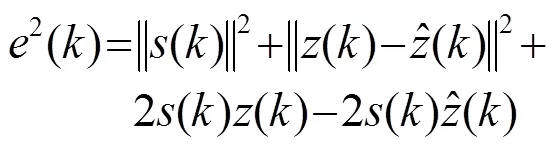
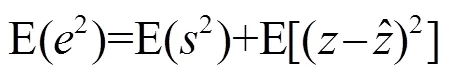
2.2 小波阈值
小波消噪原理是将含噪信号在各尺度上进行小波分解,设定一个阈值,幅值低于该阈值的小波系数置为0,高于该阈值的小波系数或者完全保留,最后将处理后获得的小波系数用逆小波变换进行重构,得到去噪后的信号。阈值去噪中,阈值函数体现了对超过和低于阈值的小波系数不同处理策略,是阈值去噪中关键的一步。
设表示小波系数,为给定阈值,sgn(.)为符号函数,常见的阈值函数有:
硬阈值函数:
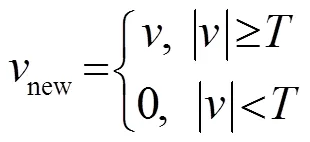
软阈值函数:
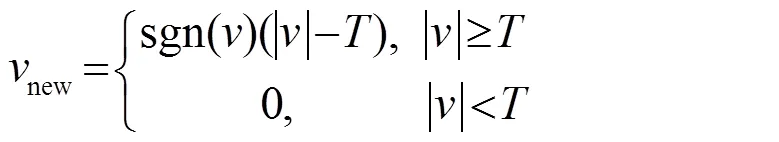
3 算法仿真实验
在实验室环境下录制语音文件。所录语音为8 kHz采样率、8 bit量化、线性PCM编码的数字语音;实验仿真结果如图3~10所示。图3是原始语音及频谱。图4是非线性函数的特性曲线,由式(6)构造得出。图5是测量语音信号与频谱,从图5中根本无法看出任何的语音信息。图6是有色噪声的估计,其频率范围与测量信号频率范围重叠。图7是经过非线性变换后的噪声信号和频谱。从图8可以看出被有色噪声污染的测量信号经过ANFIS系统消噪后,可明显分辨出语音信号。图9是经过小波消噪后的语音,消噪效果进一步优化。图10是被有色噪声污染后经过维纳滤波消噪后的语音,可见消噪效果不好,基本得不到语音信号,语音信号还是被淹没在噪声中。从图8、9与图10的对比可见,其中信噪比为=50,采用自适应神经网络模糊信号和小波消噪算法对于去除有色噪声是有效的。图11是上述方法在=3时的比较,虽然从波形上还是有噪声,但是播放时得到清晰可辨的语音,可见该算法在低信噪比下也是有效的。
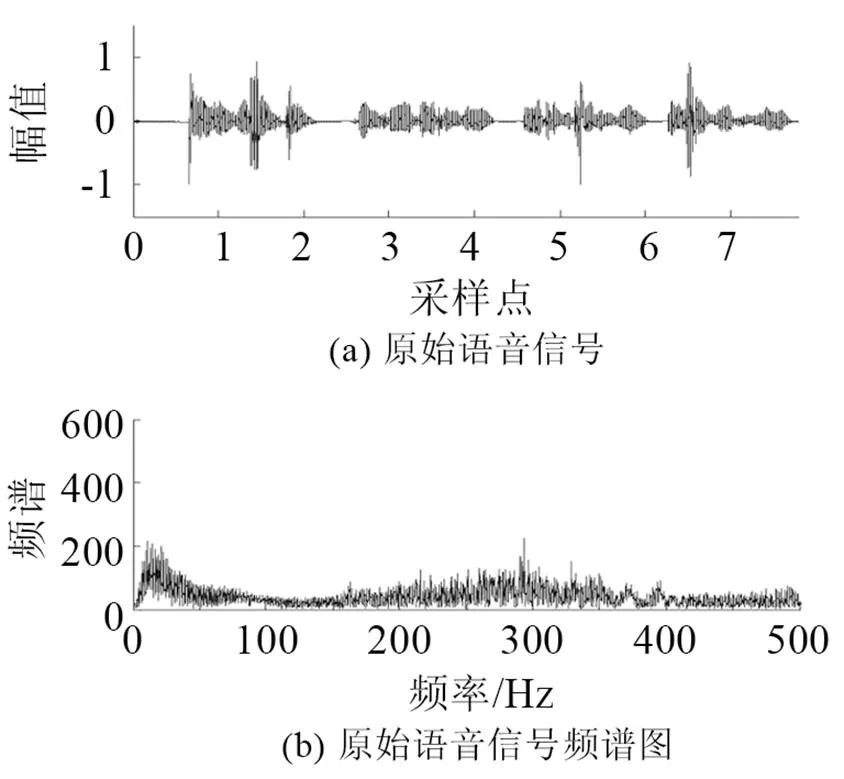
图3 原始语音及频谱

图4 特性曲线
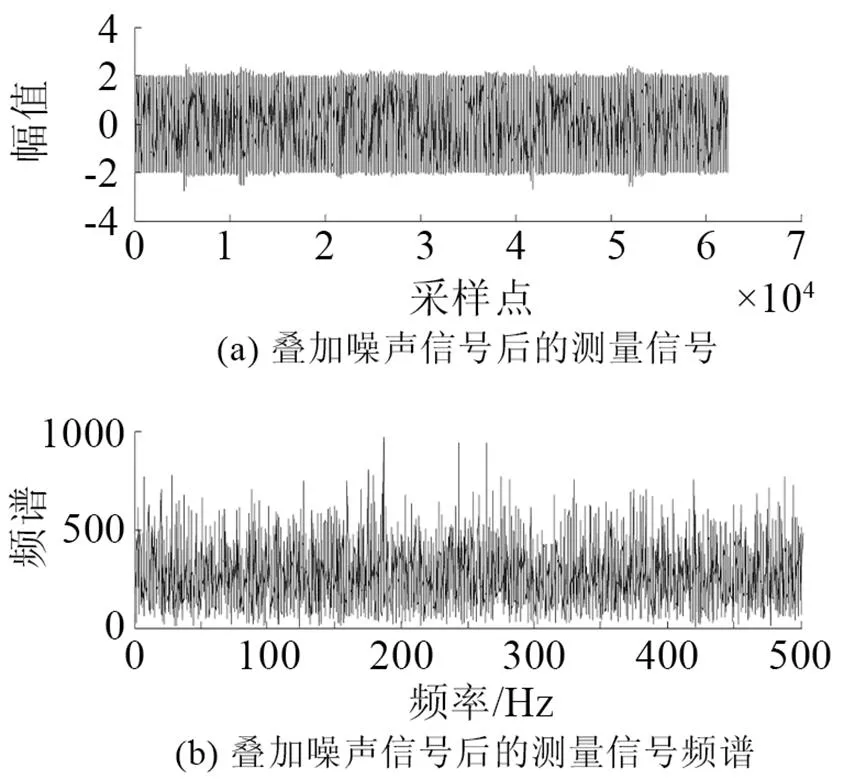
图5 叠加有色噪声的测量语音信号与频谱
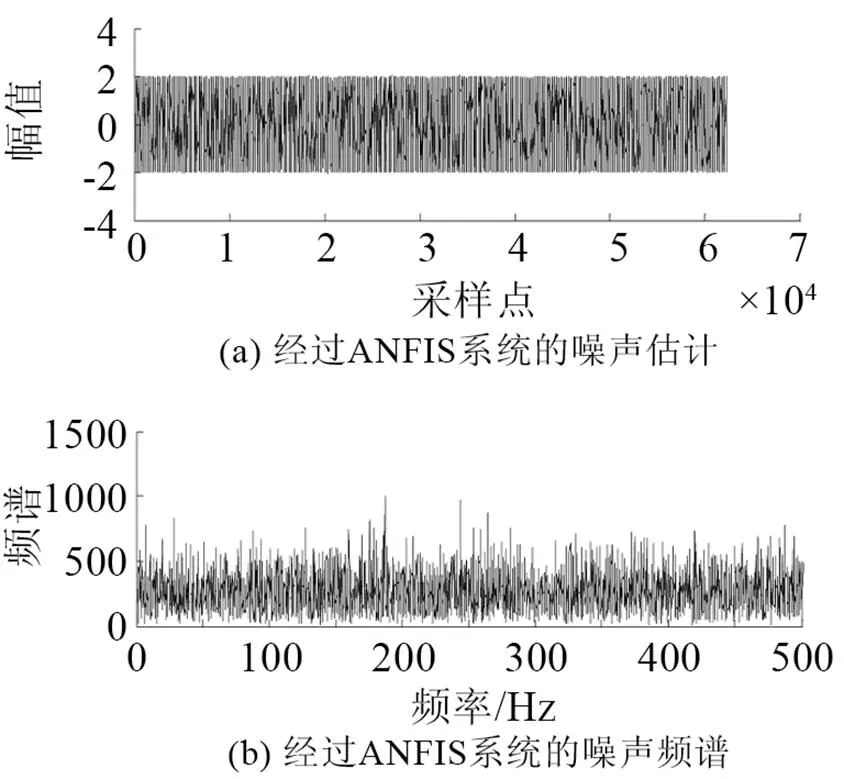
图6 经过ANFIS系统的噪声估计与频谱
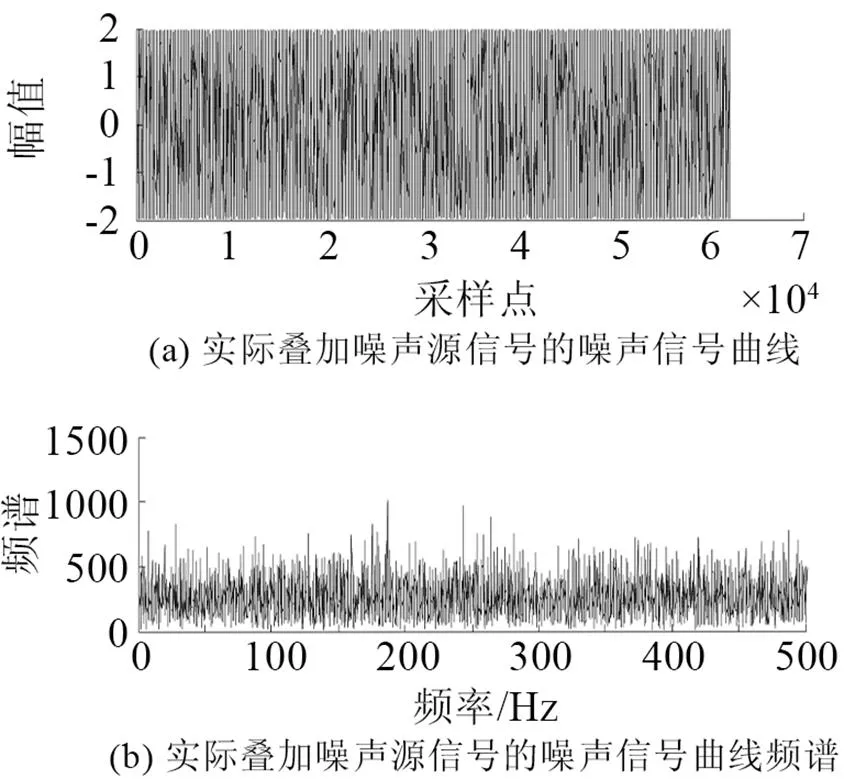
图7 经过非线性变换后的噪声与频谱
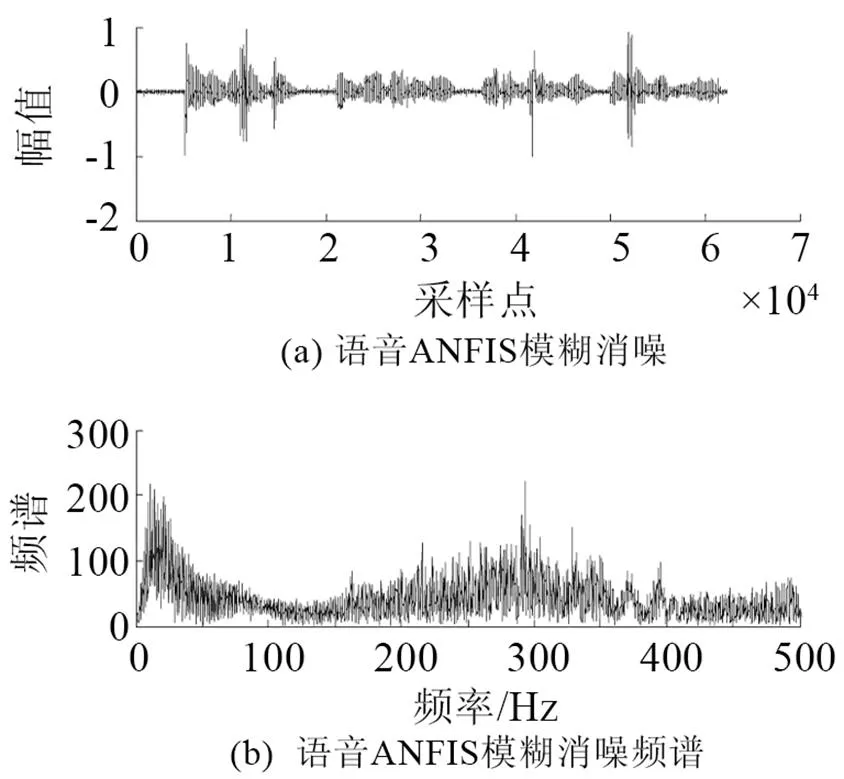
图8 经过ANFIS消噪后语音与频谱 SNR=50

图9 语音小波消噪和低频重构及频谱SNR=50

图10 语音维纳消噪
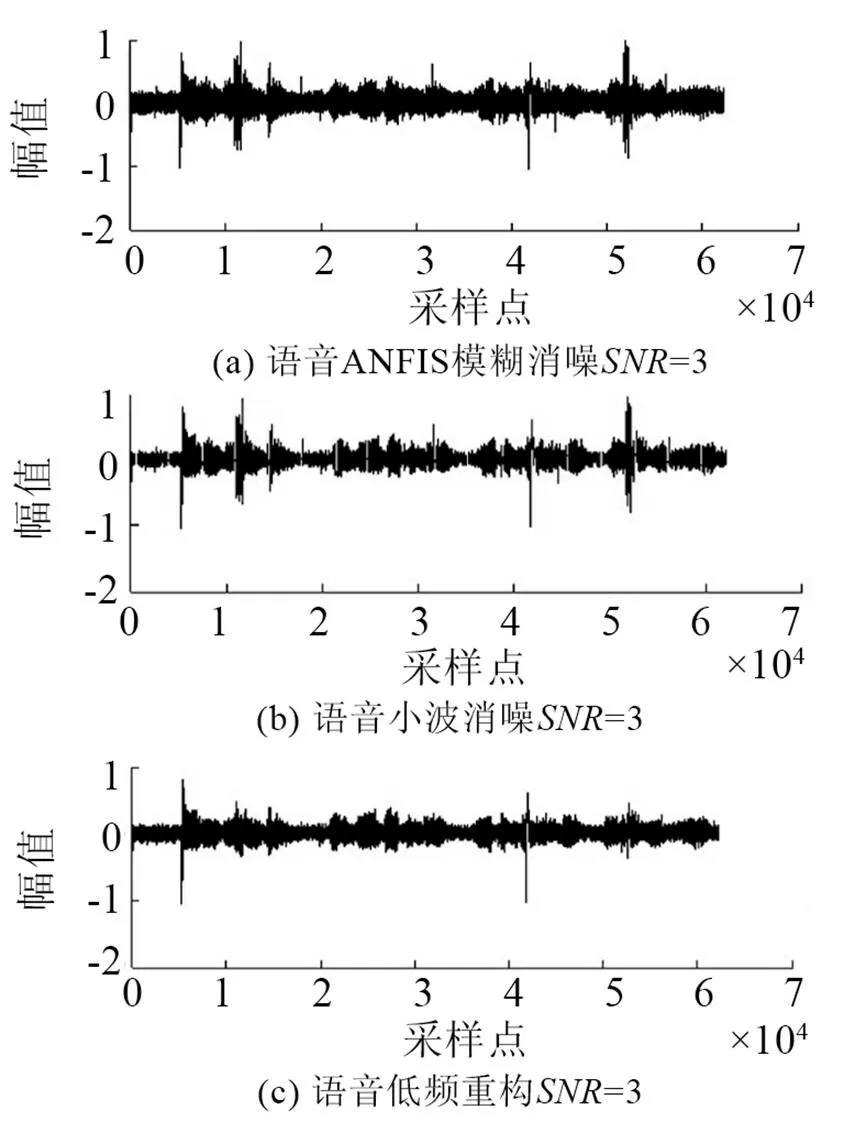
图11 SNR=3 ANFIS消噪后语音和小波消躁及低频重构语音波形
4 结论
自适应神经网络模糊小波语音消噪算法,可在未知外界干扰源特征、传递途径不断变化以及背景噪声和被测对象相似的情况下,能够有效地消除外界有色声源的干扰,获得高信噪比的语音信号,这一算法为在测试环境不太理想的工作现场做测试分析和故障诊断时,提供可靠的方法和依据。
[1] 赵晓群. 数字语音编码[M]. 北京: 机械工业出版社, 2007.
ZHAO xiaoqun, Digital speech coding[M]. Beijing: Mechanical Industry Publishing Press, 2007.
[2] PALIWAL K, BASU A. A speech enhancement method based on Kalman filtering[C]// Proc Acoustics Speech and Signal Processing, IEEE International Conference on IC A SSP' 87.[S.l.]: IEE E Press,1987, (12): 177- 180.
[3] Wiener, Norbert. Extrapolation, interpolation, and smoothing of stationary time Series[M]. New York: Wiley.
[4]signalapproach for speech enhancement[J]. IEEE Transactions on Speech and Audio Processing, 1995, 3(4): 251-66.
[5] Staib W E, Bliss N G, Staib R B. Recent developments in neural network applications - neural network conversion of the electric arc furnace into the intelligent arc furnace[C]// 1991 AISE Spring Conference, 1991.
[6] 崔先强, 杨元喜, 高为广. 多种有色噪声自适应算法的比较[J]. 武汉大学学报: 信息科 学版, 2006, 31(8): 731-735.
CUI Xianqiang YANG Yuanxi GAO Weiguang. A variety of colored noise adaptive algorithm is compared[J]. Journal of Wuhan University Information: Science Edition, 2006, 31(8): 731-735.
[7] 郭桂容. 模糊模式识别[M]. 长沙: 国防科技大学出版社.
GUO Guirong. Fuzzy pattern recognition[M]. Changsha: National University of Defense Technology Press.
[8] 张毅, 杨秀霞. 小波消噪在微弱信号检测中的应用[J]. 微计算机信息, 2006, 1(1): 113- 114.
ZHANG Yi,YANG Xiuxia. Wavelet denoising in the application of weak signal detection[J]. Journal of Micro Computer Information, 2006, 1(1): 113-114.
[9] 张乃尧, 阎平凡. 神经网络与模糊控制[M]. 北京: 清华大学出版社, 1998.
ZHANG Naiyao, Yan Pingfan. Neural network and fuzzy control [M]. Beijing: Tsinghua University Press, 1998.
[10] Widrow B. Glover J R, Mecool J, et al.Adaptive noise canceling: principles and application[J]. Proc IEEE, 1975, 63(12): 1692-1716.
[11] 楼顺天, 胡昌华, 张伟. 基于MATLAB的系统分析与设计---模糊系统[M]. 西安: 西安电 子科技大学出版社, 2005.
LOU Shuntian, HU Changhua, ZHANG wei. Based on the MATLAB system analysis and design - fuzzy system[M]. Xian Xi’an: University of Electronic Science and Technology Press, 2005.
[12] Staib W E, Bliss N G, Staib R B. Neural network conversion of the electric arc furnace into the intelligent arc furnace[C]// 74th AIME Steelmaking Conference, 1991.
Algorithm for ANFIS and wavelet denoising of speech signal
SUN Yan
(Computer Department of Qinghai University for Nationalities, Xi’ning 810007,Qinghai, China)
An ANFIS and wavelet denoising algorithm is proposed for additive colored noise. Modeling the nonlinear dynamic characteristic of noise by ANFIS and fuzzy approximating colored noise, the Auto Neural Fuzzy Inference System (ANFIS) and wavelet denoising system of speech signal is set up and trained. According to the different wavelet coefficients’ transmission properties of edge signals and noises under the different scales of the wavelet transform, the median filter is designed. Colored noise can be successfully removed by using subtraction in the original speech signal. Experimental results show that the algorithm is effective.
Auto Neural Fuzzy Inference System(ANFIS); wavelet; colored noise; denoising
TN912.35
A
1000-3630(2014)-03-232-05
10.3969/j.issn1000-3630.2014.03.010
2013-02-01;
2013-05-12
孙燕(1973-), 女, 山东青岛人, 副教授, 硕士, 研究方向为语音 处理和语音编码。
孙燕, E-mail: 453856400@qq.com

