两种非高斯海洋环境噪声统计模型分析

铁广朋，郭新毅



两种非高斯海洋环境噪声统计模型分析

铁广朋1，郭新毅2

(1. 中国科学院大学，北京 100190；2. 中国科学院声学研究所，北京 100190)

海洋环境噪声是影响声呐工作的主要因素之一，噪声模型的选取十分重要，普遍采用的高斯噪声模型在很多情况下存在局限性。引出两种非高斯噪声模型匹配实际非平稳的海洋环境噪声：广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroscedasticity, GARCH)和双模模型，通过分析两种噪声的概率密度分布函数，并与高斯模型噪声和实测海洋环境噪声比较得出两种噪声模型的适用性。GARCH(1,1)模型通过调节参数可以吻合大部分浅海和深海海洋环境噪声，双模模型则只对浅海某些情况存在适用性，而对深海吻合性较差。两种噪声模型的统计特性分析表明它们可以适用于高斯噪声模型存在局限的非平稳环境下。

非高斯海洋环境噪声；广义自回归条件异方差模型；双模模型；概率密度分布函数

0 引言

海洋环境噪声是海洋的一个重要声学特性，无论主动还是被动声呐系统，其性能都会受到海洋环境噪声的影响，对于传统的声呐系统来说它是无用的、需要抑制的。同时，海洋环境噪声对潜艇进行声隐蔽起着重要作用。海洋环境噪声包含大量有关海洋的信息，通过它可以反演获得某些重要的海洋环境参数。因此，对海洋环境噪声统计特性进行分析和研究，深刻认识海洋环境噪声的特性，建立合适的海洋环境噪声模型有着十分重要的意义。现在采用较多的噪声模型为高斯噪声，然而海洋中(特别是近海)受工业噪声源的影响，噪声的统计特性与高斯噪声模型存在差异。如今，国内外已经开始对非高斯噪声进行研究。

本文将介绍两种噪声模型，广义自回归条件异方差噪声模型(GARCH)和双模噪声模型。Engle于1982年提出的自回归条件异方差性模型(Autore- gressive Conditional Heteroscedasticity, ARCH模型)[1]，将方差和条件方差区分开来，并让条件方差作为过去误差的函数而变化，从而为解决异方差问题提供了新的途径。由于其对现代金融计量经济学发展的重要影响，Engle也因此项学术成就而获得2003年诺贝尔经济学奖。1986年，Bollerslev在ARCH模型的基础上提出了广义自回归条件异方差(GARCH)模型[2,3]，GARCH模型的变量随时间变化，在非平稳时间序列方面广泛应用，符合实际海洋环境噪声的时变特性。双模噪声模型最初是描述电子通信中的噪声，是由高斯噪声和一种非高斯噪声叠加成的简单混合噪声，双模噪声整体上来说是属于非高斯噪声，兼容了高斯噪声和一些非高斯噪声。浅海环境中噪声来源复杂多样，因此，这种叠加的双模噪声具有一定的适用性。与高斯噪声模型相比，GARCH模型的概率分布具有尖峰厚尾的特点，双模模型则相反。

1 噪声模型的数学及统计特性分析

1.1 广义自回归条件异方差噪声模型(GARCH)

GARCH模型以ARCH模型为基础改进发展而来，现如今，GARCH模型已经被应用到越来越多的时间序列分析中去[4]。GARCH模型时间序列GARCH(，)的表达式为

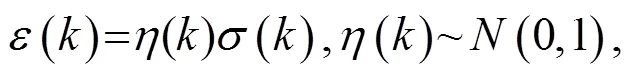
GARCH(1,1)模型条件方差为

1.2 双模噪声模型

双模模型噪声绝对值的均值为

平均功率为

分析两种噪声模型的概率密度分布函数，并与高斯噪声的概率密度分布函数进行比较。图1为三种噪声模型概率密度分布函数对比图。通过三种模型概率密度的对比图可以看出，GARCH(1,1)模型噪声概率密度分布函数最为尖锐，小振幅分量较多，即尖峰厚尾，而双模模型噪声概率密度分布函数尖端最矮，高斯噪声模型位于前两个模型中间。由于GARCH(1,1)模型和双模模型可以调节各自的参数，改变自身的尖锐程度，因此，GARCH(1,1)模型可以从高斯模型概率密度分布函数开始表现得更为尖锐，双模噪声则会自高斯模型开始更为低平。由此可见，GARCH(1,1)模型和双模模型可以通过调节参数的值作为各种环境下的海洋噪声模型。

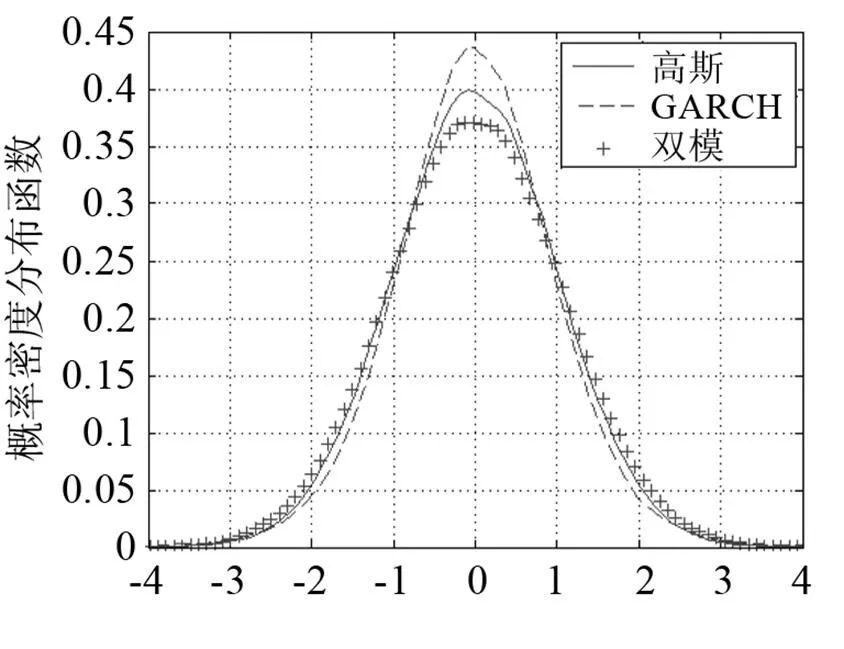
图1 高斯模型、GARCH模型和双模模型噪声序列概率密度对比

2 实际海洋环境噪声对比分析

将实际海洋中测得的噪声信号与GARCH模型和双模噪声模型进行比较。实测海洋噪声信号为南海海域环境噪声。

实验条件简介：实测噪声信号为十月份南海实验数据，深海海深为1800 m，水听器位于水深130 m，记录天数7 d；浅海海深为170 m，水听器位于水深80 m，记录天数4 d。

2.1 GARCH模型

图2 深海海域实测海洋环境噪声及GARCH模型噪声

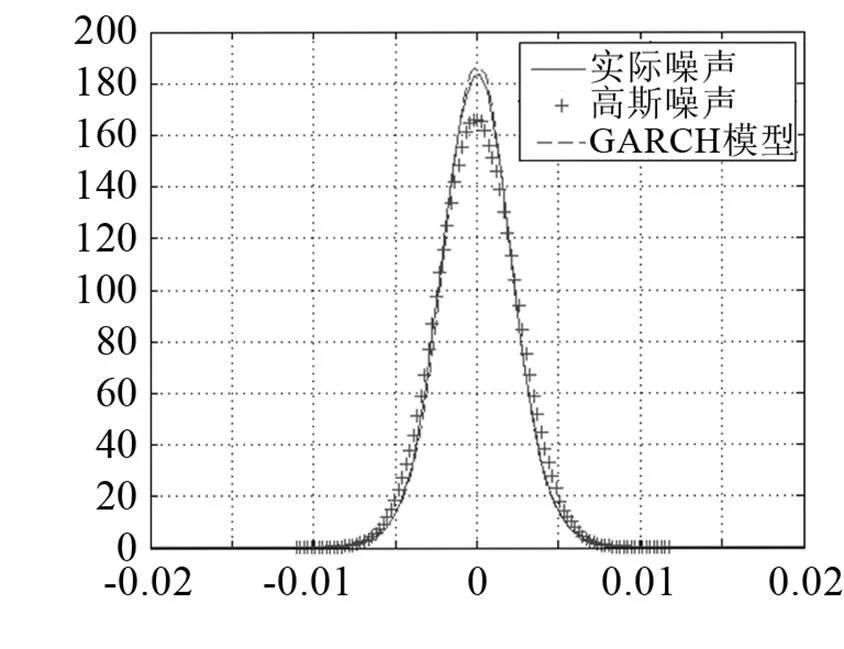
图3 GRACH模型噪声与深海实际海洋环境噪声概率密度分布

图4 浅海海域实测海洋环境噪声及GRACH模型噪声

图5 GRACH模型噪声与浅海实际海洋环境噪声概率密度分布

图6 不同取值的统计次数分布((a)：深海，(b)：浅海)

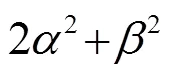
2.2 双模噪声模型

图7 四种不同参数GARCH(1,1)时间序列

图8 浅海海域实测海洋环境噪声及双模模型噪声

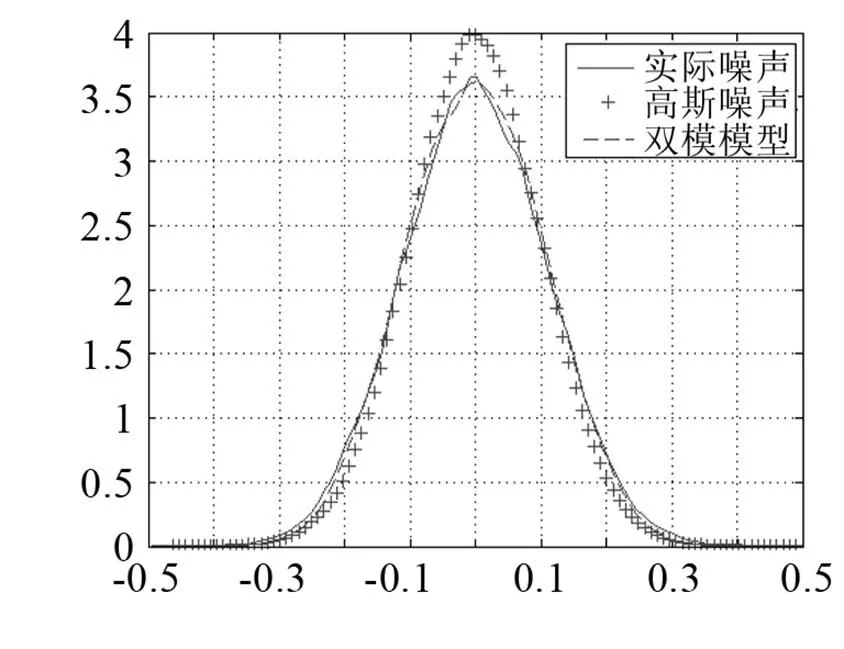
图9 双模模型噪声与浅海实际海洋环境噪声概率密度分布

3 结论

本文采用GARCH(1,1)和双模模型两种非高斯噪声模型模拟实际海洋环境噪声。实际海洋环境噪声具有一定的不稳定性和非高斯性，高斯噪声简单普遍，但很难符合实际海洋噪声的这一特性。对于这类不稳定性非高斯的噪声，GARCH(1,1)噪声模型和双模噪声模型概率密度分布函数与其具有不错的吻合性，GARCH(1,1)可以通过调节参数值来模拟大部分的海洋环境噪声(特别是深海)，对于某些GARCH(1,1)模型不适合的噪声环境，可以应用双模模型模拟，而双模噪声模型与深海的吻合性较差，两种模型在一定程度上具有互补性。文中给出了两种非高斯噪声模型模拟南海海洋环境噪声时参数的参照选取范围。结果表明，对于高斯模型存在局限性的非平稳和非高斯海洋环境噪声，可以用GARCH(1,1)和双模模型模拟。

[1] Robert F. Engle. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation[J]. Econometrica, 1982, 50(4): 987-1007.

[2] Hadi Amiri, Hamidreza Amindavar, Mahmoud Kamarei. A new underwater ambient noise modeling based on heteroscedasticity time series[C]// International Conference on New Concepts for Harbour Protection, Littoral Security and Shallow-water Acoustic Communication, 2005; Turkey, 04, July 2005.

[3] Bullerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics ,1986, 31(3): 307-327.

[4] Hadi Amiri, Hamidreza Amindavar, Mahmoud Kamarei. Underwater Noise Modeling and Direction-Finding Based on Heteroscedastic Time Series[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2007(1): 1-11.

[5] 山拜.达拉拜, 黄玉划. 几类非高斯噪声模型的转换研究[J]. 电子学报, 2004, 32(7): 1090-1093.

SENBAI Dalabaev, HUANG Yuhua. Research on models transformation of some non-gaussian noises[J]. ACTA Electronica Sinica, 2004, 32(7): 1090-1093.

[6] 黄玉划, 山拜.达拉拜. 双模噪声中信号的检测[J]. 电路与系统学报, 2002, 7(1): 37-40.

HUANG Yuhua, SENBAI Dalabaev. Detection of signals in Bimodal Noise[J]. Journal of Circuits and Systems, 2002, 7(1): 37-40.

Analysis of two kinds of non-Gaussian ocean ambient noise statistical models

TIE Guang-peng1, GUO Xin-yi2

(1.University of Chinese Academy of Science, Beijing 100190, China;2.Institute of Acoustics, Chinese Academy of Science, Beijing 100190, China)

Underwater ambient noise is one of the main factors affecting sonar performance. The selection of noise model is very important. Gaussian noise model is widely used, but in many cases limitations exist. This paper introduces two kinds of non-Gaussian noise models matching to the actual non-stationary ocean ambient noise: Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model and bimodal model. Through the analysis of the two noise model’s probability density functions (PDF) and by comparing them with the Gaussian noise model and the measured underwater ambient noise, the applicability of the two models is clarified. GARCH (1,1) can be fit for the majority of shallow and deep ocean ambient noise by adjusting the parameters. The bimodal model fits for some conditions of shallow water, not for the deep water. The statistical characteristics of the two noise models indicate that they can be used in the non-stationary cases where the Gaussian model has limitations.

non-Gaussian ocean ambient noise; GARCH model; bimodal model; probability of density function

O427

A

1000-3630(2014)-03-0209-04

10.3969/j.issn1000-3630.2014.03.005

2013-01-28;

2013-05-02

铁广朋(1989－), 男, 山东潍坊人, 硕士研究生, 研究方向为海洋环境噪声反演。

铁广朋, E-mail: tieguangpeng11@mails.ucas.ac.cn