用慢特征分析算法实现水声信号盲分离

何会会，李钢虎，要庆生，贺晓凯，石超雄



用慢特征分析算法实现水声信号盲分离

何会会，李钢虎，要庆生，贺晓凯，石超雄

(西北工业大学航海学院，陕西西安 710072)

在常规的水声信号盲处理研究中，通常都是用独立成分分析算法分离线性混合信号，而对于较复杂的非线性混合信号，独立成分分析算法无能为力。针对这种情况，提出将慢特征分析(Slow Feature Analysis, SFA)算法应用于水声信号非线性盲源分离领域。一般而言，对源信号做非线性混合变换后输出混合信号较源信号变化较快，而采用SFA算法可以从复杂的非线性混合信号中提取出变化缓慢的信号，通过仿真实验，分别对简单信号和复杂水声信号的非线性混合信号进行分离，通过将源信号与分离信号对比，发现SFA算法输出信号与源信号高度相似，验证了SFA算法在非线性盲源分离领域应用的有效性和可行性。

信号处理；盲源分离；慢特征分析

0 引言

盲源分离是盲信号处理领域中的一个重要分支，自1986年Herault J和Jutten C[1]首次提出盲源分离的概念，盲源分离经过近30年的发展，已经成为比较成熟的一门学科分支。盲源分离在雷达、通信、医学分析、图象处理、语音信号识别、阵列信号处理以及通信信号分析等众多领域有着广泛应用，得到了许多突破性成果，引起了相关学者的极大关注。

盲源分离是指在信号模型和传输通道参数未知或已知的信息非常少的情况下，仅从观测信号中分离出源信号的方法。当前多数盲源分离算法都假设源信号是统计独立的并且是线性混合的，这时我们用独立成分分析(Independent Component Analysis, ICA)方法分析，在这个问题上众多学者已经取得了丰硕的成果[2]。ICA的基本思想为：在线性混合的情况下，()=()，其中()为源信号，()为观测混和信号，为未知的混合矩阵，输出为()=()，其中为权矩阵，也是所要求的矩阵，需满足使得输出信号和源信号具有相同的形状，但不要求幅度和顺序的一致性，通常=-1，其中为置换矩阵，为对角矩阵[3]。

众所周知，水下通信系统是相当复杂的，有行船、地震波、海面波浪以及海洋湍流等噪声，因此当观察声呐接收到信号时，通常目标信号被海洋环境噪声扰乱甚至淹没，这严重阻碍了提取有用的信息。这时观测信号发生了非线性混合畸变，显然线性混合信号分离算法已不再适用，若把非线性混和模型仍视为线性混和的情况并利用线性ICA方法分离信号，可能导致错误的结果。因此，需要能更逼真地模拟海洋环境的假设模型，即非线性或者弱非线性模型。在非线性混合模型中进行信号的盲分离，在盲源分离领域称之为非线性盲源分离，慢特征分析(Slowness Feature Analysis, SFA)算法是盲源分离新近发展起来的算法，基于其特性，本文将这种算法用于水声信号分离，通过仿真研究，发现慢特征分析算法非常实用。

1 慢特征分析

1.1 慢特征

慢特征是表征信号所固有的性质，因而对于信号分离具有至关重要的作用，等同于模式识别中的不变量，慢特征指的是信号中所隐含的变化最缓慢的成分，是从混和信号中提取出来的源信号的高级表示，表征信号发生源的固有属性。

1.2 慢特征分析算法概述

慢特征分析就是从快变的复杂信号中提取慢特征的一种算法，该算法已经取得了很多的应用，例如在生物视觉中的应用，通过模拟在生物视觉中大脑是如何从观感信号中提炼出平移、旋转等慢特征的[4]。SFA在生物视觉系统中的成功应用启发我们将SFA应用于听觉系统，由此我们尝试在海洋声学环境中通过SFA的方法达到非线性盲源分离的效果。

SFA算法的目标是提取输入时序数据中所隐含的缓慢变化的成分，即除了常值信号外，变化最缓慢的成分，其算法基本思想是相关矩阵的特征值分解，其本质是在经过非线性扩展的特征空间对目标函数进行优化，寻找最优解的线性组合。它的非线性是通过增加输入变量的高阶多项式来引入的。多项式的阶数体现特征空间的复杂程度，算法的输出()包含信号本身所固有的不变量信息的程度，取决于其输入变量非线性扩展的程度[4]。

1.3 SFA算法基本原理

慢特征分析是独立成分分析算法[5]的发展，它是从快速变化信号中提取慢信号特征的算法。SFA可以得到变化速率从小到大排列的一系列特征。

满足约束条件：

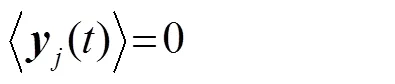
值得指出的是，从输入到输出是瞬时的，因此处理速度是非常快的，但得到的却是信号的慢特征，而这是低通滤波器所不能达到的效果，因为低通滤波器处理信号是有延时的，且滤波器会滤除高频成分，而慢特征分析算法只是优先提取出变化缓慢的成分。

接下来分两种情况讨论：

(1) 线性

则式(2)可写为

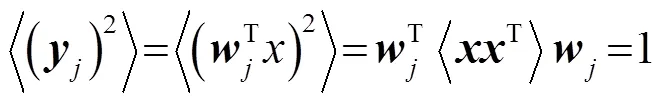
将式(5)和(6)结合可以得到

由矩阵论的知识可以知道，使上式成立的权向量为式(8)的广义特征向量

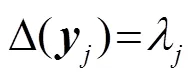
根据矩阵论的知识，式(7)的极小化问题为求Rayleigh商的极小值点，则

(2) 非线性

到此为止，总结慢特征分析算法如下：

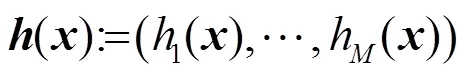
1.4 SFA应用于盲源分离

众所周知，独立分量分析用于线性盲源分离，而在非线性盲源分离中，仅有独立性的约束已不能分离混合信号了，将慢特征分析算法用于盲源分离是基于以下原因：若对源信号做非线性混合，混合后的信号要比源信号变化得更快，最简单的例子就是对正弦波做平方运算可以得到频率加倍的信号，变化更快。由于慢特征分析算法可从复杂多变的信号提取出慢变的信号，所以考虑将其应用于盲源分离，认为提取出的慢变信号即为源信号的近似。

2 仿真实验结果

矩阵形式为

图1为两个源信号波形图，图2为两个源信号经过上述线性非线性线性混合后的信号，图3为将混合信号作为基于二阶多项式扩展的SFA算法的输入信号生成的前两个输出信号，在1.4节中提到过，SFA用于盲源分离的原因在于其可以从复杂变换信号中提取慢特征，认为提取出的慢特征即为源信号的近似估计。本实验采用的源信号较简单是为了通过观察就可以将源信号与分离信号做对比。图3与图1对比发现，SFA算法可以成功地实现非线性盲源分离，本实验属于理论研究，对实际应用具有一定启示作用。

图2 (a)混合信号x1 (b)混合信号x2

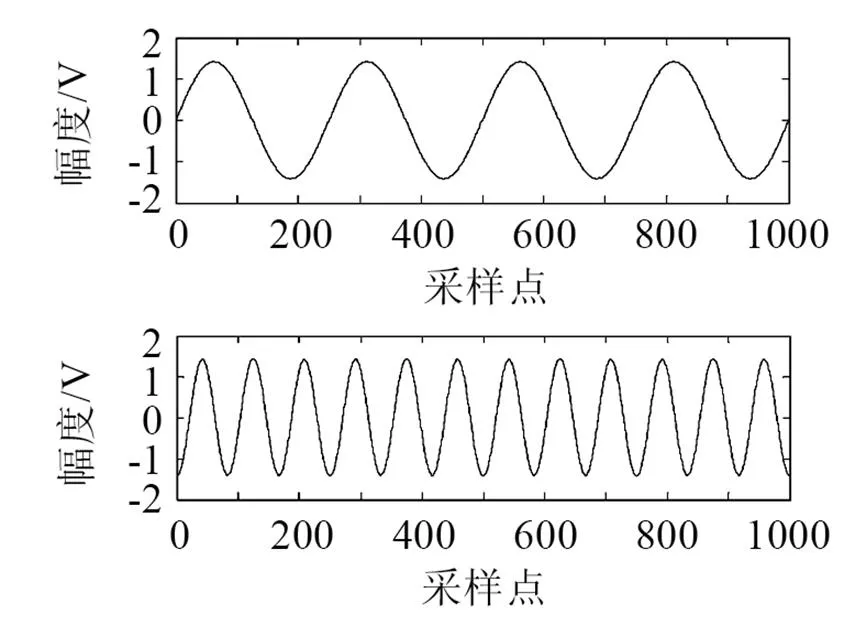
图3 SFA输出信号

实验一中采用的是基于二阶多项式扩展的非线性情况下的SFA算法，由1.3节知，对于二维信号，SFA输出为5个，这里只取与源信号数目相同的前个输出，这也说明了SFA适用于源信号数目已知的盲源分离算法。除前个输出外，其他为源信号的高阶非线性形式。

仿真实验二：源信号采用海狮和鲸鱼的叫声，信号采样频率为44100 Hz，采样点数取5000个，混合模型同实验一所采用的模型相同。

图4 (a)鲸鱼叫声 (b)海狮叫声

图5 (a)混合信号x1 (b)混合信号x2

图6 SFA输出信号

实验二和实验一采用不同的源信号、相同的混合模型，实验结果表明，SFA算法不仅可以分离简单信号的非线性混合信号，也可以分离复杂信号的非线性混合，且分离信号与源信号相似度较高。分离简单信号的效果优于分离复杂信号的效果，说明SFA性能与源信号有关。从输出信号中也可以看出，SFA输出信号按照信号变化快慢的程度排列，变化越慢的信号，输出越靠前，与ICA输出次序不确定相比的又一优点。

图7 (a) 源信号s1和s2的散点图 (b) 混合信号x1和x2散点图 (c) SFA分离信号散点图 (d) ICA分离信号散点图

3 结语

本文提出将慢特征分析算法应用于水声信号盲处理中，并取得了很好的效果，通过仿真验证了算法的有效性和可行性。但是目前由于完全非线性混合盲分离问题的复杂性，现有的非线性混合信号盲分离算法研究的都是较简单的非线性混合的情况，对更一般的非线性混合信号的可分离性以及可分离的充要条件需作进一步的研究。

[1] Jutten C, Herault J. Blind separation of sources, Part I: An adaptive algorithm based on neuromimetic[J]. Signal Processing, 1991, 24(1): 1-10.

[2] 郑春厚. 独立分量分析算法及其应用研究[D]. 安徽: 中国科学技术大学博士论文, 2006.

[3] Comon Pierre. Independent Component Analysis, A New Concept?[J]. Signal Processing, 1994, 36(3), 287-314.

[4] Wiskott L, Sejnowski T. Slow feature analysis: unsupervised learning of invariances[J]. Neural Computation, 2002, 14(4): 715- 770.

[5] Blaschke T, Berkes P, Wiskott. What is the relationship between slow feature analysis and independent component analysis?[J]. Neural Computation, 2006, 18(10): 2495-2508.

[6] Blaschke T, Zito T, Wiskott L. Independent slow feature analysis and nonlinear blind source separation[J]. Neural Computation, 2007, 19(4): 994-1021.

Blind source separation of underwater acoustic signals by using slowness feature analysis

HE Hui-hui, LI Gang-hu, YAO Qing-sheng, HE Xiao-kai, SHI Chao-xiong

(Institute of Acoustic Engineering,Northwestern Polytechnical University,Xi’an710072,Shaanxi, China)

In conventional blind underwater acoustic signal processing,the independent component analysis algorithm is often used to separate linear mixed signals. However, for the more complex nonlinear mixed signal, the independent component analysis algorithm is helpless. To solve this problem, this article applies slow feature analysis to blind underwater acoustic signal processing. In general, the nonlinear mixed signal varies faster than the source signal does, and SFA algorithm can extract slowly varying features from complex nonlinear signals. Through simulation experiment, the nonlinear mixed signals of simple signals and complex underwater acoustic signals are separated.By comparing the source signals and the separated signals, it is found that the output signals of SFA correlate to the source signal highly. It proves that SFA is effective and practicable in the field of nonlinear blind source separation application.

signal processing; blind source separation; slowness feature analysis

TB566

A

1000-3630(2014)-03-0270-05

10.3969/j.issn1000-3630.2014.03.017

2012-12-24;

2013-03-19

何会会(1990－), 女, 陕西榆林人, 硕士研究生, 研究方向为水声 信号与信息处理。

何会会, E-mail: hehuihui15@163.com