基于马尔科夫模型的污染物质量浓度变化规律

覃春乔，陈 星，张其成，王卫平

(河海大学水文水资源学院，江苏南京 210098)

基于马尔科夫模型的污染物质量浓度变化规律

覃春乔，陈 星，张其成，王卫平

(河海大学水文水资源学院，江苏南京 210098)

采用马尔科夫模型模拟调水过程中太浦河练塘大桥断面处污染物质量浓度变化过程，并通过构建转移矩阵，确定进步度，对污染物质量浓度的变化情况进行动态评价，研究污染物质量浓度变化规律。结果表明，调水指标的进步度计算结果整体为正，但局部地区出现负值;随着调水量的增加，水体自净能力增强，各指标的进步度普遍提高;调水试验结束进入水资源常规调度期间，水质长时间保持良好。本研究旨在为制定河湖连通调水方案提供借鉴。

污染物质量浓度;马尔科夫模型;进步度;引江济太

太湖流域地形地貌特征独特，流域内河网密集，水面平缓，在径流和潮汐的双重作用以及人类活动的强烈影响下，河道内的水流动性差。太浦河是连接太湖和黄浦江的通道。太浦河及黄浦江一线不仅是太湖洪水的主要下泄通道，而且是流域下游上海、杭嘉湖地区的主要来水水源。上海市根据黄浦江上游来水的水质和水量情况，规划从东太湖调水，以改善黄浦江上游供水水源地的水质。2002年建设的引江济太工程，就是通过太浦河增加黄浦江上游的供水量，改善太浦河下游及黄浦江的水质。

在江河湖连通的条件下，水资源引清调度是保持河流水系连通性、维持河湖健康的重要手段。分析水资源引清调度的效果，以确定高效经济的水资源调度方案，可从水体流动性和水质水环境容量的改善情况来进行。

分析水质变化情况，探索各项污染物质量浓度的变化规律，近年来所采用的方法有很多，归纳起来主要有:模糊可变集合理论［1］，基于灰色系统理论的灰色法［2］，神经网络法［3］，AHP 法以及主成分分析法［4］。江湖河连通过程中污染物质量浓度的变化受到多种不确定因素的影响，污染物从一个状态转移到另一个状态具有一定的随机性。基于数学表达式的水质预测模型很难将这些因素都考虑进去，水质评价定性模型也很难考虑所有影响因素。污染物质量浓度的变化过程是一种具有马尔科夫特性的随机过程，笔者采用马尔科夫模型研究江河湖连通调水过程中典型断面上污染物质量浓度的变化规律，并通过构建转移矩阵确定进步度的方法对污染物质量浓度变化情况进行动态评价。

1 马尔科夫模型原理

马尔科夫模型因安德烈·马尔科夫而得名。马尔科夫过程是一种无后效性的随机过程。一个系统的状态转换过程中第n次转换获得的状态常决定于第n-1次的结果，与n-1次之前的状态无关;这种时间和状态都处于离散状态的马尔科夫过程称为马尔科夫链［5］。

假设系统的状态空间为E={E1，E2，…，En}，而在每一个时间系统只能处于其中一个状态，因此每一个状态都有n个转向(包括转向自身)，即，Ei→E1，Ei→E2，…，Ei→Ei，…，Ei→En。

在m时刻系统处于状态Ei的条件下，在m+k时刻系统处于状态Ej下的条件概率可表示为

当k=1时，即系统在m时刻处于状态Ei、在m+1时刻处于状态Ej的条件概率，称为由状态Ei经一次转移到状态Ej的转移概率。系统所有状态的一步转移概率的集合所组成的矩阵称为一步状态转移概率矩阵，其形式为

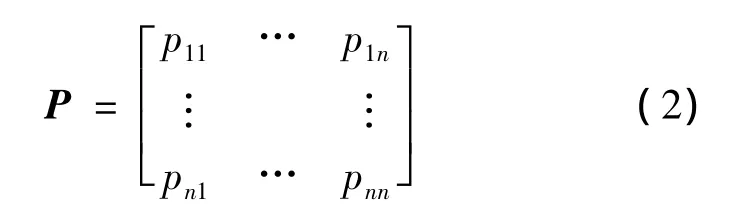
此矩阵具有以下两个性质:①非负性:pij≥0，i，j=1，2，…，n;②行元素之和为1，即

由一步转移概率的定义可知，k步转移概率为系统由状态Ei经k次转移到状态Ej的概率，可表示为［6］

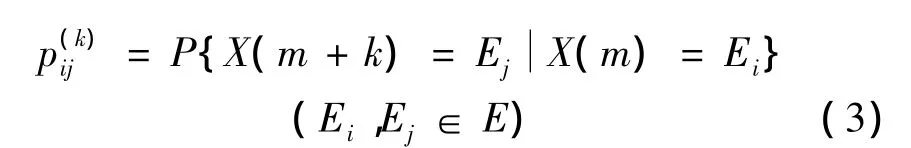
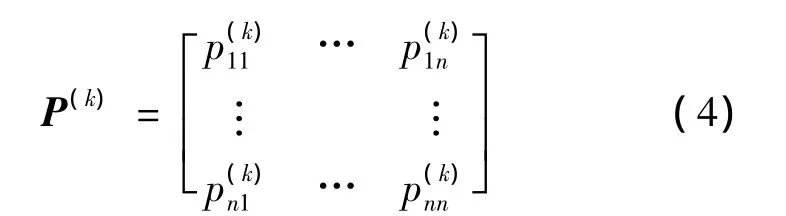
因此，系统的k步转移概率矩阵就是由所有状态的k步转移概率集合所组成的矩阵，其形式为

1.1 指标归一化处理

采用传统的Zadeh规格化公式［7］:

越大越优型:

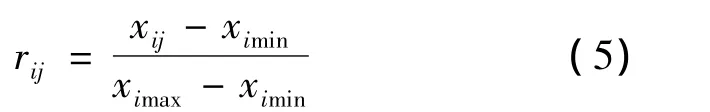
越小越优型:

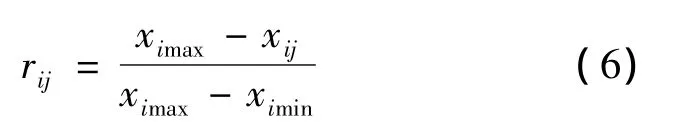
式中:xij为第i项指标第j项状态的值;ximax为第i项指标所有状态的最大值;ximin为第i项指标所有状态中的最小值;rij为规范化后的第i项指标第j项状态的值。

在评价指标中，有的指标特征值变化范围较大，有的变化范围小，在规格化过程中，就会夸大特征值变化范围较小的指标在评价中的相对作用，使评价结果偏离实情。利用改进的Zadeh公式可克服该缺点。改进的Zadeh公式为

1.2 划分质量状态

根据所要评价水环境的特点和实际需要，将水环境质量状态划分为N个级别，对于有限个状态空间表示为E={1，2，…，N}。最常见的根据水环境质量标准中水质类别，将指标值划分为6个状态。实际情况中，某一个指标的监测值大量集中在一个水质类别中，若单纯按照水质分类，将达不到判断水质变化趋势的目的。此时按水质分类的方法不适用，需要人为规定隶属范围更小、隶属度更精细的状态划分标准［8］。

本文将规格化后的指标划分为11个质量状态，即E={1，2，…，11}，具体划分见表 1。

表1 马尔科夫规格化后指标质量状态划分

考虑水环境改善力度以及目标效果尽可能最优，将上述临界点状态下的值归属于较高状态区间。划分质量状态之后，对每个指标规格化后的值将其隶属到某个状态内，得到指标隶属矩阵R=rij∈E。

1.3 求各指标权重

采用离差最大化赋权法，令wmax=1，其余权重按比例相应放大，即

离差最大化赋权法公式［9］为

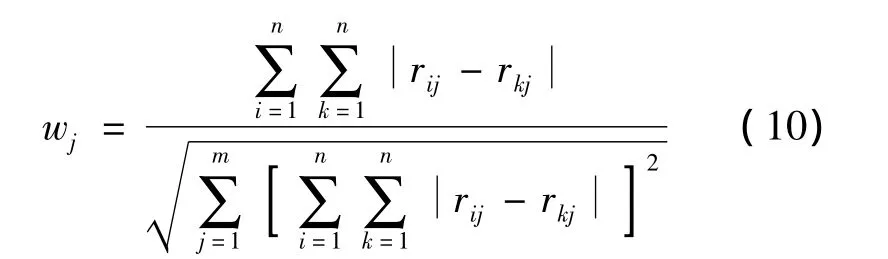
式中:wj为第j项指标初始权重;W'为指标规范化后的权重;rkj为规范化后的第k项指标第j项状态的值;m为指标数，n为监测次数。确定初始矩阵A，矩阵A中的数值采用进一法原则进行整数化。

1.4 求概率转移矩阵

得到初始矩阵后，便可根据指标隶属矩阵来计算转移矩阵。假设共有m个指标进行了n次监测，在这n次监测中，相邻的两次监测指标由i级转变成j级的总数为kij，i，j=1，2…，11，且默认第n次监测值转为本身，i级内的原始样本的数为Ki，则i级j级的转移概率［10］pij为

转移矩阵即为P=(pij)N×N(N为划分状态的个数)。

1.5 求绝对进步度

由计算得到的转移矩阵P已可对水质的未来发展进行预测，也可对监测期内的水质动态发展有一个大致的了解，但为了更明确地显示水质的变化情况，需要做进一步计算，在此引入进步度［11］的概念。

假设:①水质改善，进步度为正;水质恶化，进步度为负;②水质改善或恶化越明显，进步度的绝对值越大［8］。

根据以上假设，定义进步度sij为

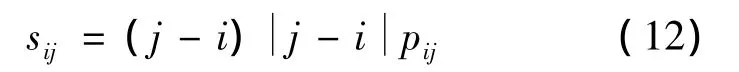
式中:i，j=1，2…，11，则 s=(sij)N×N称为概率转移矩阵P的进步矩阵，，称为绝对进步度。

1.6 求相对进步度

为了更易于比较各指标的动态发展情况，需要将d(s)进行规格化，使水质改善最大的相对进步度为1，水质恶化最严重时的相对进步度为-1，限定相对进步度D(s)的范围为［-1，1］。

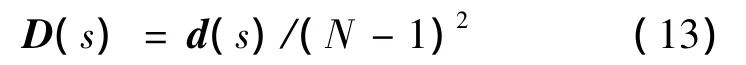
式中，N为划分状态的个数，本研究中，N=11［12］。

进步度是一个范围在［-1，1］之间的数。这个数大于零，说明污染物指标质量情况是改善的，反之则是恶化的。进步度绝对值越大，说明水质改善或恶化的程度越大。进步度是一个概率统计参数，可以宏观定量分析水质水量的关系，不受个别突变值的影响。

2 实例应用

练塘大桥位于太浦河下游，是控制黄浦江水质的重要断面。表2为太浦河练塘大桥断面在调水试验期间的实测流量和水质情况(这里将CODMn、NH3-N、TP、TN、引水流量5个指标作为水环境安全的指标体系)。

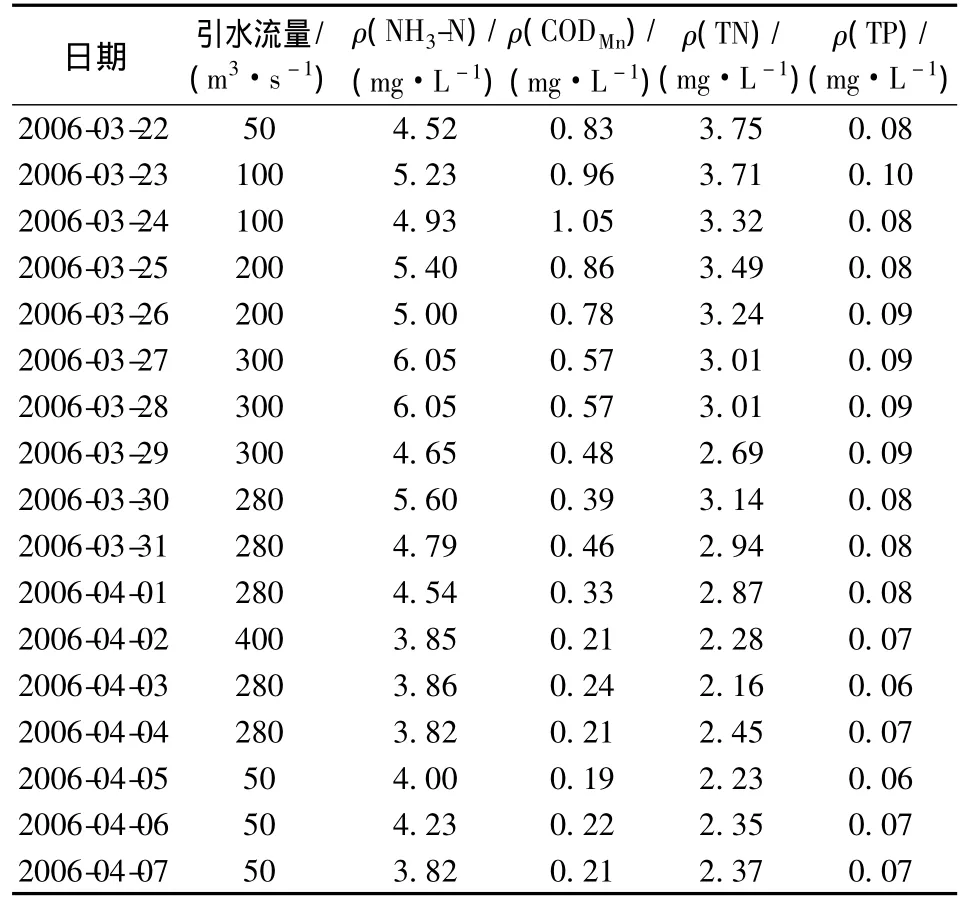
表2 太浦河练塘大桥断面引水流量和水质情况

根据质量状态划分标准，将太浦河练塘大桥实测的流量数据以及水质数据划分隶属度矩阵R。根据离差最大化赋权法公式，通过matlab程序编写求得初始矩阵E以及权重。

其中，w=(1，0.2621，0.9272，0.2864，0.3447)T。

已知流量的基础上，CODMn的影响力变化程度大于其他指标因子。通过CODMn变化情况由公式求得练塘大桥马尔科夫转移概率矩阵为

建立matlab程序求解进步度结果为

由图1看出，调水指标相对进步度计算结果整体为正，局部地区出现负值，并且随着调水流量的增加，污染物自净能力增加，各指标进步度普遍提高，调水试验结束后的水资源常规调度期间，相对进步度为正，说明水质长时间保持良好。

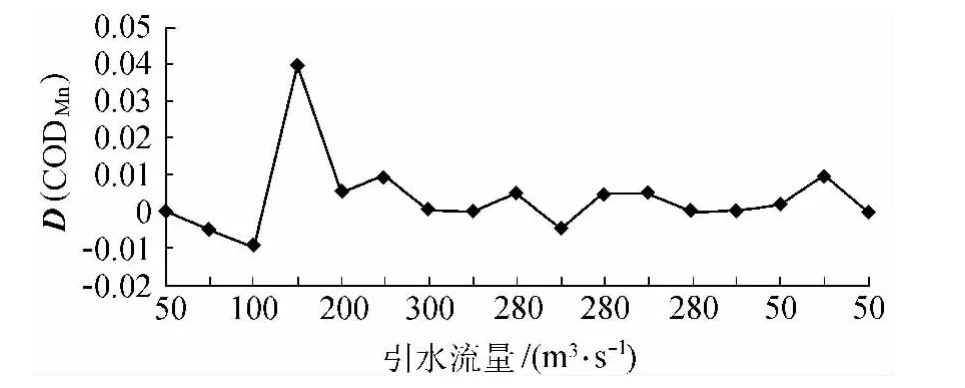
图1 CODMn相对进步度计算曲线

当引水流量达到300 m3/s时，太浦河向外排水，此时，太浦河水体污染物质量浓度随着流量的增加而降低，水质趋好。当引清比小于1时，由于太浦河支流的水质多为劣Ⅴ类，可视为点污染源，加之流域内面源污染，使得引水水量不足以稀释污染物，且太浦河水流流速加快，导致底泥污染物释放，加剧了太浦河的污染。从图1可以看出，某些节点的水质在引水过程中降低，其原因是引水路线上的河道污水在水位抬高过程中汇入了太浦河，导致水质变坏。而在长期引水过程中，还出现水质恶化的情况，这需要考虑重点污染区域是否存在污水大量偷排的问题。

3 结语

利用马尔科夫模型计算水质状态转移概率矩阵，历史数据越多，预测结果就越可靠。当数据量较少时，所得出的转移矩阵不能真实地反映水质变化规律。状态矩阵的随机性较强，应综合利用其他水质模型进行综合对比分析，以更好地预测水质的变化情况。

［1］张弛，郭瑜，李伟，等.基于模糊可变集合理论的地下水质量综合评判［J］.水电能源科学，2007，25(4):17-18.(ZHANG Chi，GUO Yu，LI Wei，et al.Use of variable fuzzy sets method for evaluating groundwater quality［J］.HydroelectricEnergy，2007，25(4):17-18.(in Chinese))

［2］章新，贺石磊，张雍照.水质评价的灰色关联分析方法研究［J］.水资源与水工程学报，2010，21(5):117-119.(ZHANG Xin，HE Shilei，ZHANG Yongzhao.Study on grey relational analysis method for water quality assessment［J］.Journal of Water Resources ＆ Water Engineering，2010，21(5):117-119.(in Chinese))

［3］兰文辉，安海燕.环境水质评价方法的分析与探讨［J］.干旱环境监测，2002，16(3):167-169.(LAN Wenhui，AN Haiyan.Discussion on methods of water quality assessment［J］.Arid Environmental Monitoring，2002，16(3):167-169.(in Chinese))

［4］王维，纪枚，苏亚楠.水质评价研究进展及水质评价方法综述［J］.科技情报开发与经济，2012，22(13):129-130.(WANG Wei，JI Mei，SU Yanan.Reviews of the progress in the research of water quality evaluation and the methods forwaterqualityevaluation［J］. Sci-Tech Information Development＆ Economy，2012，22(13):129-130.(in Chinese))

［5］程万里，李亦芳，郝伏勤，等.黄河三门峡段基于马尔科夫模型的水质预测［J］.电力环境保护，2008，24(3):7-9.(CHENG Wanli，LI Yifang，HAO Fuqin，et al.The water quality forecast of Sanmenxia reach based on Markov model［J］. Electric PowerEnvironmental Protection，2008，24(3):7-9.(in Chinese))

［6］陈启明，陈华友.基于Markov链的最优化模型在长江水质预测中的应用［J］.安徽工业大学学报:自然科学版，2011，28(1):78-82.(CHEN Qihua，CHEN Huayou.Optimal model and its application in forecasting water resource of Yangtze River based on Markov chain［J］.Journal of Anhui University of Technology:Natural Science，2011，28(1):78-82.(in Chinese))

［7］张又，刘凌.“引江济太”调水中望虞河水质变化的规律［J］.水资源保护，2013，29(2):53-55.(ZHANG You，LIU Ling.Variation of water quality of Wangyu River during water diversion from Yangtze River to Taihu Lake［J］.Water Resources Protection，2013，29(2):53-55.(in Chinese))

［8］李学法，王守峰.基于马尔科夫模型的区域水环境安全评价［J］.安徽农业科学，2012，40(28):13902-13905.(LIXuefa，WANG Shoufeng. Waterenvironment assessment based on Markov model［J］.Journal of Anhui Agricultural Sciences，2012，40(28):13902-13905.(in Chinese))

［9］陈华友.多属性决策中基于离差最大化的组合赋权方法［J］.系统工程与电子技术，2004，26(2):194-197.(CHEN Huayou. Combination determining weights method for multiple attribute decision making based on maximizing deviations［J］.Journal of Systems Engineering and Electronics，2004，26(2):194-197.(in Chinese))

［10］何斌，陈灿.水质动态评价的马尔柯夫方法［J］.环境工程，2003，21(2):60-63.(HE Bin，CHEN Chan.Markov method of dynamic assessment on water quality［J］.Environment Engineering，2003，21(2):60-63.(in Chinese))

［11］邱林.基于模糊权马尔可夫模型的综合水质预测［J］.人民长江，2007，38(1):75-78.(QIU Lin.Prediction of comprehensive water quality Markov model based on fuzzy right［J］.Yangtze River，2007，38(1):75-78.(in Chinese))

［12］冯江浪.改进灰色马尔科夫模型及其在水资源预测中的利用［J］.物探化探计算技术，2010，32(1):9-13.(FENG Jianglang.Improvement of gray Markov model and its application to water resources forecasting［J］.Computing Techniques for Geophysical and Geochemical Exploration，2010，32(1):9-13.(in Chinese))

Variation of pollutant concentration based on Markov model

QIN Chunqiao，CHEN Xing，ZHANG Qicheng，WANG Weiping
(College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China)

In this study，the Markov model was used to simulate the variation of the pollutant concentration at the Liantang Bridge section during the process of water diversion from the Yangtze River to Taihu Lake.Through the construction of the transfer matrix，the degree of progress was determined，and the dynamic variation of the pollutant concentration was evaluated.The results show that the calculated degree of progress of the water diversion indicator was positive，with negative values in some areas;with the increase of diverted water，the self-purification capacity of contaminants improved，and the degrees of progress of all indicators increased;and the water quality has been high for a long time during the water resources regular scheduling since the trial water diversion was completed.This study aims to provide references for the establishment of water diversion schemes for connected rivers and lakes.

pollutant concentration;Markov model;degree of progress;water diversion from Yangtze River to Taihu Lake

X522;X132

A

1004-6933(2014)03-0056-05

10.3969/j.issn.1004-6933.2014.03.011

水利部公益性行业科研专项基金(201001030)

覃春乔(1988—)，男，土家族，硕士研究生，研究方向为水文学及水资源。E-mail:873910321@qq.com

(收稿日期:2013-09-18 编辑:彭桃英)